合理猜想 层层验证——以“圆的周长”教学为例

江苏省宿迁市泗阳众兴实验小学（223700） 张前侠

合理猜想层层验证
——以“圆的周长”教学为例

江苏省宿迁市泗阳众兴实验小学（223700） 张前侠

在小学数学课堂教学中让学生拥有猜想—推理—验证—发现规律的过程，便是一个学生“乐学、会学、活学”的过程。通过大胆猜测、合情推理、实践验证，不仅能够促使学生主动获取知识，增强思维的强度，而且有利于培养学生的直觉思维，发展学生的推理能力。

猜测推算验证

本节课以直观图为依据，让学生在猜测、推算、验证、测量、计算、分析的基础上，深入思考，推算出圆周率的范围，把学生的思维逐步引向深入。

一、观察验证，初步感知圆的周长与直径有关

师（出示3个大小不同的车轮）：这是3个大小不同的车轮，如果把这3个车轮分别向前滚动一周，猜猜看哪一个车轮会滚得更远一些？说说理由。

师：真的是第三个车轮会滚得更远一些吗？一起来看大屏幕。（课件演示）

图1　

师：车轮滚动一周的长度实际上就是车轮的周长。观察一下，在这三个车轮中，哪个车轮的直径最短？哪个车轮的周长最短？哪个车轮的直径最长？哪个车轮的周长最长？

师：车轮的直径越短，车轮的周长也就——（越短）车轮的直径越长，车轮的周长也就——（越长）这就说明圆的周长肯定与圆的什么有关系？

【评析：通过情景图呈现三个车轮滚动的情景，以及“猜猜看哪一个车轮会滚得更远一些？”揭示所要学习的内容是圆的周长。】

二、推理验证，分析推理圆的周长与直径有怎样的关系

师：圆的周长和直径之间可能会有怎样的关系呢？会是倍数关系吗？下面我们接着研究。

师：这是一个等边三角形，从名字来看就知道等边三角形三条边长度都相等。现在用6个完全相同的等边三角形拼成了一个——正六边形。

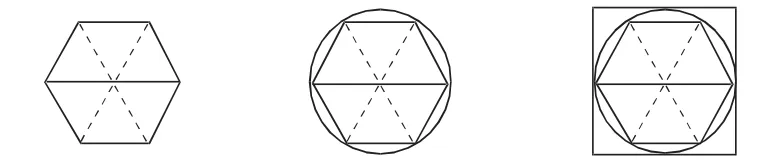
图2　

师：正六边形的周长是圆的直径的几倍？圆的周长可能是它直径的3倍吗？我国古代有一个说法——圆出于方！这个正方形和圆有怎样的联系？

师：正方形的周长是边长的4倍，怎么没有人猜圆的周长也是直径的4倍呢？那圆的周长可能是直径的4倍吗？请在小组里讨论。

师：综上所述，你认为圆的周长是它直径的几倍？请在小组内讨论。

【评析：这里的推理，需要学生进行深入思考，通过将圆的周长与正方形和正六边形进行比较，让学生有依据地去想。通过多媒体动态演示三图合一的过程，将学生的思维引向“将三图联系起来进行推算，从而合理地估计出圆的周长与直径的倍数范围”。数据测算之前先进行倍数范围的推想，有利于学生对文本的学习产生深层次的反思与感悟。】

三、实践验证，深入研究圆的周长与直径之间的倍数关系

师：研究数学光有猜想不行，还需要实践的检验。下面将对刚才猜想的结果进行验证。

师：老师给每个小组准备了一些材料和一张研究记录表，4人一组，2人合作测量，1人记录数据，1人用计算器计算。

师：同样是荧光圈，怎么量出的周长不一样呢？

师：由于是测量，所以总会存在一定的误差！

师：研究表完成了，我们一起来看看（表略）。几种不同的圆，周长不同，直径也不同。通过比较，你发现了什么？

师：大多数同学实验得出“一个圆的周长总是它直径的3倍多一些”。（板书：3倍多一些）是的，一个圆的周长总是它直径的3倍多一些，与我们刚才的推想“比3倍多却又比4倍少”相吻合！因为测量时总会存在误差，所以我们小组研究只是得到一个大概的倍数。事实上，任何一个圆的周长除以直径的商都是一个固定的数。想知道这个3倍多一些的数叫什么吗？请自学课本93页的内容。（板书：圆周率可以用字母π表示）

【评析：直面学生的一知半解，通过实践操作回应结果的存在性。通过观察、比较、归纳实验数据，使学生发现“圆的周长总是直径的3倍多一些”这一事实。】

在小学数学课堂教学中让学生拥有“猜想—推理—验证—发现”的过程，便是一个充满个性的过程。通过大胆的猜测、合情的推理、实践的验证，不仅能够促使学生主动获取知识，增强思维的强度，而且有利于培养学生的直觉思维，发展学生的推理能力。

（责编童夏）

G623.5

A

1007-9068（2016）23-037