基于钢束优化配置的PC梁桥长期变形控制*
薛兴伟, 庞 兴, 孙聚阳
(沈阳建筑大学 交通工程学院, 沈阳 110168)
基于钢束优化配置的PC梁桥长期变形控制*
薛兴伟, 庞兴, 孙聚阳
(沈阳建筑大学 交通工程学院, 沈阳 110168)
针对大跨度预应力混凝土箱梁桥普遍出现的长期变形过大的问题,通过对预应力钢束配置进行优化,降低最大悬臂施工阶段的初始位移,进而减小过大的长期变形,达到挠度控制的目的.构建单位预应力的挠度矩阵,以挠度为控制目标,利用ANSYS进行钢束优化求解得到钢束最优配置.结果表明,优化设计后的挠度较恒载零弯矩法减小40%.利用ANSYS进行钢束优化设计的方法对预应力混凝土箱梁桥的长期变形控制具有良好的效果.
大跨度; PC梁桥; 优化设计; 影响矩阵; 挠度控制; 钢束配置; 悬臂施工; 恒载零弯矩法
由于结构徐变的长期发展和预应力配置等原因,大量预应力混凝土箱梁桥普遍出现了许多不同性质的裂缝和挠度过大等问题,而且随着桥梁跨度的增大,呈现出更为严重的现象[1-2].
梁桥悬臂施工经历了悬臂、合拢并施加二期恒载过程,然后进入运营阶段.桥梁下挠主要为施工过程中最大悬臂状态的挠度f1,合拢后施加二期恒载的挠度,即成桥挠度f2,则桥梁在成桥后时间t下总挠度值为
ft=[1+φ(t,t0)]f2
(1)
因徐变φ(t,t0)的计算具有很大的不确定性[3-4],通过减小最大悬臂状态的挠度f1进而减小成桥挠度f2,达到最终减小ft的控制方法,该方法已成为研究的方向.恒载零弯矩法[5-8]是一种以挠度控制为目的而提出的钢束配置方法,此方法在2012年2月出版的公路桥涵设计手册《梁桥》[9]中作为大跨PC梁桥基本配束原则所呈现,标志着对这一方法的接受和正式推广.本文将优化结果和恒载零弯矩法的钢束配置进行了对比.
1 钢束优化配置
大跨PC梁桥不仅要满足强度计算的要求,同时还需要考虑在合理钢束配置下,尽量减小跨中下挠,以控制后期挠度的进一步过度发展和防止过大下挠带来的危害.但目前进行最优设计还具有较大的困难,桥梁悬臂施工计算中需考虑施工阶段、预应力及损失和截面特性等,分析具有很强的专业性,需要桥梁工程专业软件进行分析.现主流的桥梁工程专业软件中,如Midascivil和桥梁博士等均不具备二次开发、优化设计功能,使得实际应用中缺少高效可行的工具.ANSYS虽然作为一个优秀的优化设计工具,但是作为通用有限元软件,在解决桥梁工程专业问题中存在着很多的局限.因此,本文提出将专业软件与通用软件相结合的方法,即将专业软件中全过程施工分析得到的必要数据读取到通用软件中进行数据处理,从而达到目的.
在本次研究实际操作过程中,采用Midascivil软件建立全过程施工阶段分析模型,主要考虑自重和单位预应力,读取最大悬臂状态自重作用下的自重挠度和各阶段单位预应力作用在各个节段产生的预应力位移.
模型中每个节段施加钢束单位面积(100 mm2)时,将节段单位预应力钢束对主梁挠度影响的单位矩阵计入数组,就可以得到单位预应力的节段位移,即
(2)
式中:PSij为j节段施加预应力钢束在i节点产生的位移;DFP1上标“1”表示钢束单位面积产生的位移量.将每个节段乘以阶段施工时施加的钢束数量Aii,就可以得到实际钢束产生的位移DFP,即

(3)
对式(3)进行每行求和,可得到i节点在钢束作用下的位移,即

(4)
再将预应力荷载位移与恒载位移求差,得到i节点位移为
DFi=DFP(i,j)-DFSFi
(5)
优化设计的目的就是控制DFi,即在一定预应力材料数量下求得钢束配置方式,使得DFi最小.
2 预应力钢束优化程序开发
本文通过一个25 m悬臂梁来说明优化过程,该悬臂梁为5个节段,每个节段5 m,按照5个施工步骤进行.悬臂梁截面由3.0 m×1 m渐变到1.5 m×1 m,采用C50混凝土.悬臂梁配置为钢束T1~T5,钢束中心距离梁上缘15 cm,节段1配置钢束T1,节段2配置钢束T2(T2起点为固结端,终点为悬臂端),以此类推,如图1所示(单位:m).

图1 悬臂梁构造Fig.1 Structure of cantilever beam
程序主要是构建一个二维数组,并对数组进行优化求解,共分为以下5个部分.
第1部分:数组定义.定义一个二维数组,数组行数为阶段数(stg),与列数为2stg+4对应.悬臂梁为5个节段,有5个施工阶段,故建立一个5×14的数组.
第2部分:基本参数输入.第1~stg列,输入对应式(2)中从专业程序读取的每个节段预应力钢束对主梁挠度影响的DFP1.对于该悬臂梁,在1~5列输入节段1~5单位预应力的位移,主要程序语言如下:
zn=1(节段1部分)
*SET,df1(1,zn,1),0.032 6(设定节段1张拉的单位面积预应力在节段1处产生的位移值PS11)
zn=2(节段2部分)
*SET,df1(1,zn,1),0.032 56(设定节段2张拉的单位面积预应力在节段1处产生的位移值PS12)
*SET,df1(2,zn,1),0.139(设定节段2张拉的单位面积预应力在节段2处产生的位移值PS22)
……
第3部分:定义参数和数组运算.程序中对应式(3)进行AiPSij计算得到DFP,结果存储在第stg+1~2stg+1列;按照式(4)求解DFP(i,j),并存储于第2stg+2列;在列2stg+3中输入恒载作用下每个节点的挠度DFSFi;按照式(5)求解DFi,并存储于第2stg+4列.主要程序语言如下:
psa1=3(假定第1节段钢束数量,后期进行优化)
psa2=5(假定第2节段钢束数量,后期进行优化)
……
zn=(stg+2)(节段1,单位预应力乘以钢束面积得到位移)
*SET,df1(1,zn,1),df1(1,1,1)*psa1
zn=(stg+3)(节段2,单位预应力乘以钢束面积得到位移)
*SET,df1(1,zn,1),df1(1,2,1)*psa2
*SET,df1(2,zn,1),df1(2,2,1)*psa2
……
zn=(2*stg+2)(求预应力总挠度)
*DO,zq,1,stg
df1(zq,zn,1)=df1(zq,7,1)+df1(zq,8,1)+df1(zq,9,1)+df1(zq,10,1)+df1(zq,11,1)
*END DO
zn=(2*stg+3)(输入恒载挠度)
*SET,df1(1,zn,1),2.548 01
*SET,df1(2,zn,1),9.014 96
……
zn=(2*stg+4)(求恒载位移与预应力位移之差)
*SET,df1(1,zn,1),df1(1,zn-2,1)-df1(1,zn-1,1)
……
*SET,df1(5,zn,1),df1(5,zn-2,1)-df1(5,zn-1,1)
第4部分:定义相关参数以优化设计.通过APDL命令求各节段节点的最大挠度(dfmin),将该挠度最小值作为优化设计目标值,同时定义钢束总重(wps),将其作为优化控制变量,程序语言如下:
dfmin=df1(1,zn,1)
*DO,zq,2,5
*if,df1(zq,zn,1),Lt,dfmin,then
dfmin=df1(zq,14,1)
*endif
*END DO
wps=(5*psa1+10*psa2+15*psa3+20*psa4+25*psa5)*7 850*100*0.001*0.001
第5部分:优化设计.每个节点的钢束数量定义为变量DV,其变化范围为3~30.优化的目标是以恒载零弯矩法钢束质量775.6 kg为限制条件,求解在整个悬臂梁配置不超过775.6 kg钢束质量条件下,节段最小挠度对应的钢束配置.主要程序语言如下:
opvar,wps,sv,,775.6,0.001(设定钢束质量上限)
opvar,dfmin,obj,,,0.001
执行优化设计得到30个优化序列,其中,第13序列冠以*为最佳序列.从优化结果可以看出,最终得到钢束总质量为773.72 kg,未超过设定钢束质量上限.优化后挠度为-2.63 mm,比零弯矩法优化挠度-15.2 mm少12.57 mm.此时第1~5节段分别配置钢束面积823、333、305、2 529、1 438 mm2,趋势上是小悬臂少配束,大悬臂多配束,图2显示出优化序列9、10、13及14.
图3为挠度对比图,由图3可见,通过钢束的优化,本文方法较恒载零弯矩法的挠度减小82.7%.
3 实桥钢束优化设计
新兴江大桥主桥跨径为(45+70+45) m,下部结构为单肢薄壁墩,上部结构为桥宽16.75 m的单箱双室箱梁.根部梁高为4.2 m,跨中梁高为2 m,梁高变化段采用二次抛物线过渡.利用本文程序对悬臂段顶板钢束进行优化设计.
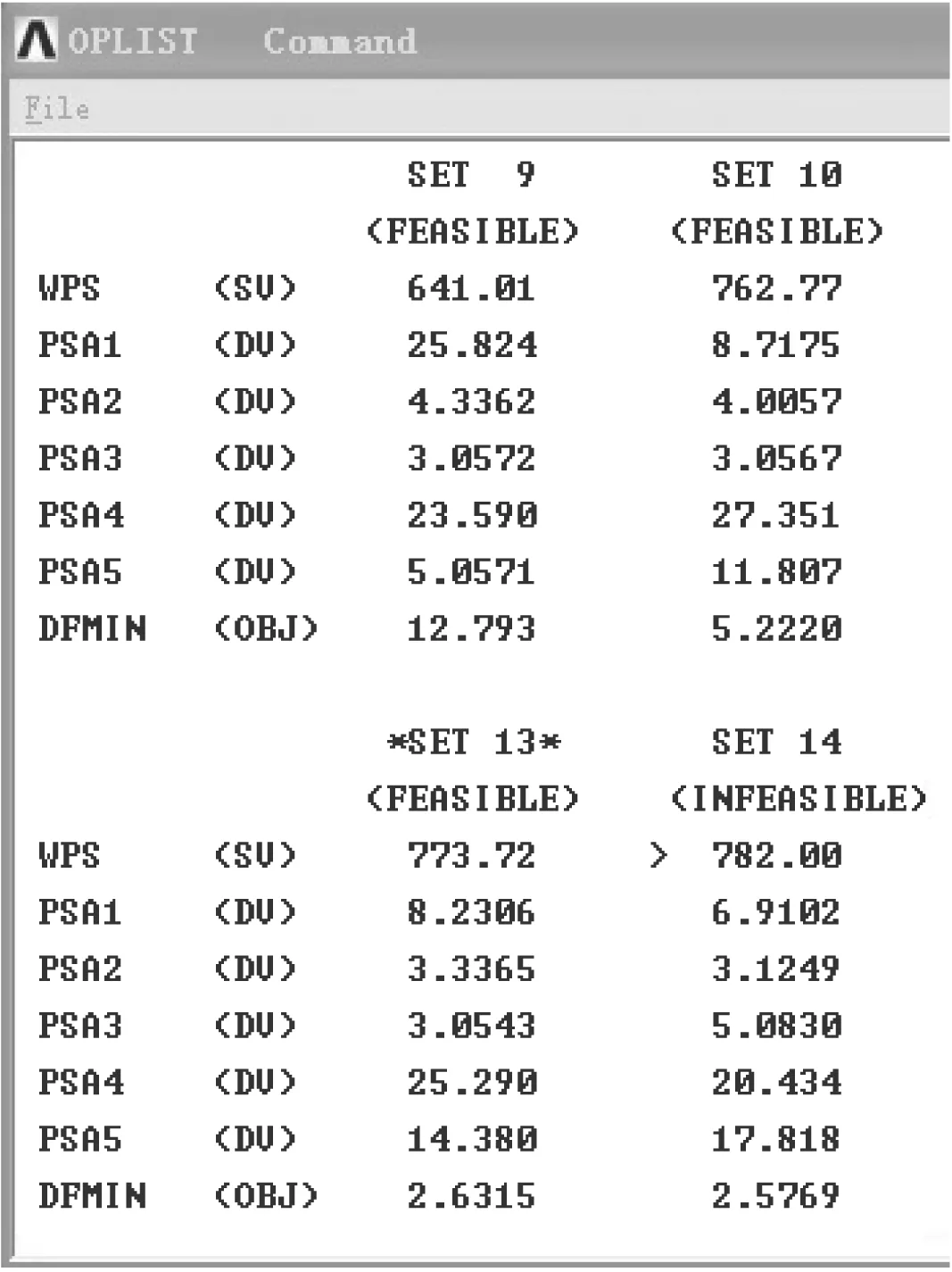
图2 悬臂梁优化序列Fig.2 Optimization sequences of cantilever beam

图3 不同钢束配置方法的挠度对比Fig.3 Deflection comparison between different steel cable configuration methods
新兴江钢构桥按照恒载零弯矩法计算得到每个T构顶板束钢束总质量为21 608 kg,编制顶板钢束优化程序时,将顶板束钢束质量作为限制条件,因程序计算时取半T构,故顶板束钢束质量为21 608/2 kg.顶板钢束根数优化范围为5~15根,经过计算得到20个优化序列.图4为新兴江大桥钢束优化序列.
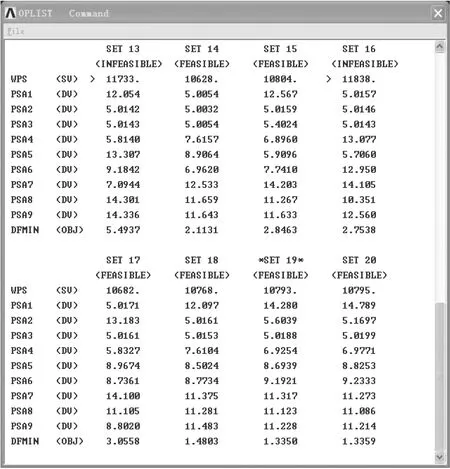
图4 新兴江大桥钢束优化序列Fig.4 Optimization sequences of Xinxingjiang bridge
序列19在节段1上配置钢束根数为14根,其他节段形式上也基本符合“小悬臂配小束,大悬臂配大束”的配束形式.与最优解1.335 mm的下挠值相差仅0.5 mm,因此,依照序列1进行设计,T1~T3采用5根,T4~T6采用8根,T7~T9采用12根,最终悬臂挠度为1.885 mm,钢束质量为10 761 kg,方案如表1所示.

表1 钢束配置方案Tab.1 Schemes for steel cable configuration
将设计结果带入实际模型进行再次计算得出,最大悬臂经优化法进行钢束调整得出最大悬臂处挠度为-8.5 mm,相当于原下挠-17.2 mm的49.4%,对比曲线如图5所示.
经中跨合拢施加二期恒载后,经过10年徐变,挠度为下挠-4.5 mm;而零弯矩法成桥10年后挠度为-11.2 mm.优化法跨中挠度为恒载零弯矩法的40%,对比曲线如图6所示.
4 结 论
本文利用ANSYS程序编写了确定悬臂阶段预应力钢束配置的优化设计程序,通过程序可以得到一定材料数量下钢束的最优配置和最小挠度.通过在专业软件中得出的结果建立预应力位移单位矩阵,在ANSYS中进行优化设计,该方法高效可行.ANSYS作为一个通用有限元软件可以在专业数据为基础的条件下,高效准确地完成分析和优化设计功能.
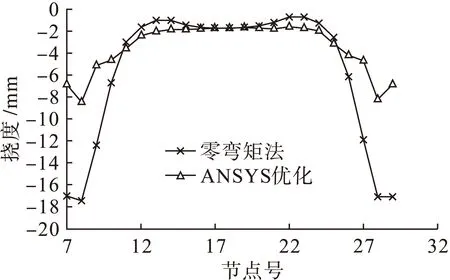
图5 最大悬臂阶段挠度对比Fig.5 Deflection comparison at state of maximum cantilever
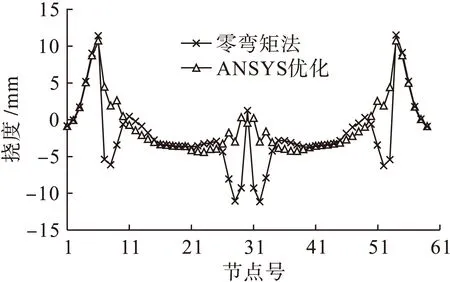
图6 成桥10年时挠度对比Fig.6 Deflection comparison within 10 years after completion of bridge construction
悬臂梁和新兴江大桥的实践均得到较好的挠度控制效果,较恒载零弯矩法有较大的改善.
[1]Takacs P E.Deformations in concrete cantilever bridges:observations and theoretical modelling [D].Norway:The Norwegian University of Science and Technology,
2002.
[2]徐仲卿,袁泉,杨振坤,等.早龄期混凝土力学性能试验及其单轴本构模型 [J].沈阳工业大学学报,2015,37(1):92-96.
(XU Zhong-qing,YUAN Quan,YANG Zhen-kun,et al.Mechanical property experiment and uniaxial constitutive model for concrete at early age [J].Journal of Shenyang University of Technology,2015,37(1):92-96.)
[3]陈三安,陈云海.混凝土桥梁徐变计算对比研究 [J].公路,2014(11):90-96.
(CHEN San-an,CHEN Yun-hai.A comparative study on creep calculation of concrete bridge [J].Highway,2014(11):90-96.)
[4]Kristek V,Kohoutkova A.Excessive deflections of concrete bridges affect safety,maintenance and ma-nagement [C]//Proceedings of the 3rd International Conference on Bridge Maintenance,Safety and Ma-nagement.Porto,Portugal,2006:355-356.
[5]温婷.恒载零弯矩在波形钢腹板PC桥中的运用 [D].南昌:华东交通大学,2013.
(WEN Ting.Dead load zero benging moment in the corrugated steel web application of PC bridge [D].Nanchang:East China Jiaotong University,2013.)
[6]刘桂生.悬臂施工连续梁桥分阶段预应力设计 [C]//第九届全国混凝土及预应力混凝土学术交流会.中国,昆明,1996:242-249.
(LIU Gui-sheng.The design of cantilever construction prestressed continuous beam bridge [C]//The Ninth National Concrete and Prestressed Concrete Academic Exchanges.Kunming,China,1996:242-249.)
[7]王法武,石雪飞.大跨径预应力混凝土梁桥长期挠度控制研究 [J].公路,2006(8):72-76.
(WANG Fa-wu,SHI Xue-fei.A study on long-term deflection control of long span prestressed concrete girder bridge [J].Highway,2006(8):72-76.)
[8]姚强.基于荷载平衡法的大跨径PC连续刚构桥长期挠度控制方法研究 [D].西安:长安大学,2009.
(YAO Qiang.Resear on long-term deflection control of the long-span PC continuous rigid frame based on load-balancing method [D].Xi’an:Chang’an University,2009.)
[9]刘效尧,徐岳.梁桥 [M].北京:人民交通出版社,2012.
(LIU Xiao-yao,XU Yue.Beam bridge [M].Beijing:China Communications Press,2012.)
(责任编辑:钟媛英文审校:尹淑英)
Long-term deformation control of PC beam bridge based on steel cable configuration
XUE Xing-wei, PANG Xing, SUN Ju-yang
(School of Traffic Engineering, Shenyang Jianzhu University, Shenyang 110168, China)
In order to solve the general problem that the long-term deformation of long-span prestressed concrete(PC) beam bridge is too large, the prestressed steel cable configuration was optimized to reduce the initial displacement at the construction stage of maximum cantilever, and then the overlarge long-term deformation was reduced so as to achieve the goal of deflection control. The unit prestressed deflection matrix was established. In addition, with taking the deflection as the optimization objective, the optimal steel cable configuration was obtained through the solution of steel cable optimization with ANSYS. The results show that the deflection after optimization design decreases 40% than that obtained with the dead load zero bending moment method. The method for the optimization design of steel cable configuration with ANSYS has good effect on the control of long-term deformation for the PC beam bridge.
long-span; PC beam bridge; optimization design; influence matrix; deflection control; steel cable configuration; cantilever construction; dead load zero bending moment method
2015-08-27.
住房和城乡建设部科学技术计划项目(2015-K5-013,K42016015).
薛兴伟(1979-),男,贵州丹寨人,副教授,博士,主要从事旧桥检测与加固及桥梁抗震等方面的研究.
10.7688/j.issn.1000-1646.2016.04.20
TM 343
A
1000-1646(2016)04-0476-05
*本文已于2016-03-02 16∶42在中国知网优先数字出版. 网络出版地址: http:∥www.cnki.net/kcms/detail/21.1189.T.20160302.1642.012.html

