纤维缠绕复合材料起伏区域残余应力
和欣辉,韩小平
(1 西北工业大学 力学与土木建筑学院,西安 710129;2 西安交通大学 机械结构强度与振动国家重点实验室,西安 710049)
纤维缠绕复合材料起伏区域残余应力
和欣辉1,2,韩小平1,2
(1 西北工业大学 力学与土木建筑学院,西安 710129;2 西安交通大学 机械结构强度与振动国家重点实验室,西安 710049)
针对纤维交叉起伏区域残余应力,建立一种细观分析模型。基于热传导方程、固化反应动力学模型和复合材料层合理论,采用有限元方法和细观分析模型,对缠绕复合材料在固化工艺过程中的残余应力分布及其变化规律进行数值模拟。通过算例,研究纤维起伏区域残余应力的分布特点,结果表明:起伏纤维束不同位置处残余应力差别很大,层合区纤维束呈现拉应力状态,起伏区纤维束呈现压应力状态,富树脂区出现最大压应力;残余应力沿纤维束起伏方向呈现V型变化趋势,在纤维束上不同位置出现拉、压不同的应力状态,起伏角度最大处出现最大压应力。
纤维缠绕复合材料;固化过程;残余应力;纤维束交叉起伏;细观模型
在缠绕复合材料制造过程中,固化温度和不同的固化周期直接影响树脂体系的固化程度,在固化和降温过程中会产生残余应力。复合材料中残余应力同时存在于树脂、纤维以及树脂和纤维界面间。纤维缠绕过程中还会出现一种特殊情况,即不同缠绕方向的纤维铺层交叉起伏,在局部区域形成富树脂区,当固化后冷却时,此处更易引起热收缩和残余应力,并且其尺度范围会明显影响残余应力的形成及分布。复合材料中残余应力的存在对其力学性能有重要影响,甚至可能引起缠绕结构的破坏和失效。近十多年来,国内外学者在残余应力的测试和数值模拟方面做了许多工作。Gopal等[1]用数值模拟方法研究复合材料层板成型过程中的升温和降温速率,发现升温速率快、降温速率慢均有利于减小残余应力。Tarsha-Kuridi等[2]把模压成型中的压力和树脂作为黏弹性参量加入到经典层合板理论中,通过数值模拟计算和实验研究,发现减小成型压力有利于减小残余应力。Zhang等[3]根据Lame方程建立计算模型,模拟多层圆柱壳上覆盖层和基层中残余应力,结果显示,可以通过控制覆盖层材料、各基层厚度及材料性能参数等改变残余应力的分布。文献[4,5]利用三维有限元方法研究纤维/树脂复合材料固化成型工艺过程中温度场、固化度场、应力场相互耦合的问题以及残余应力分布和影响因素。赵玉萍等[6]利用弹性-软化内聚力模型研究了残余应力对界面剪切应力的影响以及残余应力所引起的界面软化和脱粘。胡照会等[7]对带有铝板的复合材料层板固化全过程的残余应变/应力进行了数值模拟。王建花等[8]根据圆筒的弹性力学理论,同时考虑到复合材料加工固化过程中的温度和缠绕角度等参数的变化,建立了纤维增强复合材料身管的热残余应力模型。黄其忠等[9]研究了复合材料网格结构软模共固化成型工艺中工艺间隙、固化周期、固化度场分布以及固化过程中残余应力。马豪等[10]研究了热压成型过程中,不同固化温度对亚麻纤维及其增强复合材料力学性能的影响。结果显示当固化温度达到180℃时,亚麻纤维损伤较为严重,其增强复合材料的拉伸强度和冲击强度均发生明显的下降,但是复合材料的拉伸模量随着成型温度的升高有一定幅度的提升。
为了有效分析缠绕复合材料交叉起伏区域残余应力,本工作建立了一种细观分析模型。基于热传导方程、固化反应动力学模型和复合材料层合理论,采用有限元方法对缠绕复合材料在固化工艺过程中的残余应力分布及其变化规律进行了数值模拟。通过算例,研究了纤维起伏区域固化工艺过程以及残余应力的分布特点。
1 纤维交叉起伏区域残余应力的数值模拟
1.1交叉起伏区域细观模型及其离散化
缠绕复合材料结构在整体上可看作是由一系列重复的菱形块组成,如图1所示,因此只需分析一个菱形块的细观结构即可。菱形特征单元内又可划分为两种区域,即层合区域和纤维交叉起伏区域。由于预制件的固化成型工艺过程以及缠绕张力的作用,纤维束之间存在相互交叉挤压,使得纤维束截面形状发生改变。在交叉起伏区域,纤维束的缠绕次序依次为:纤维束1→2→3→4,如图2所示,可以看到纤维束由矩形截面改变为近似的1/4椭圆截面。
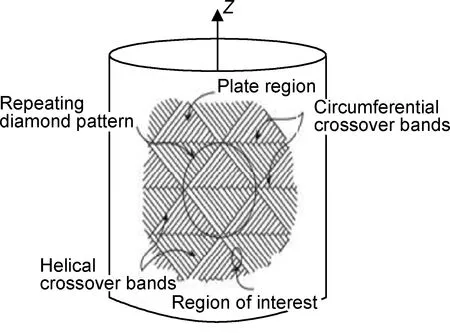
图1 纤维缠绕复合材料结构Fig.1 Structure of filament-wound composites
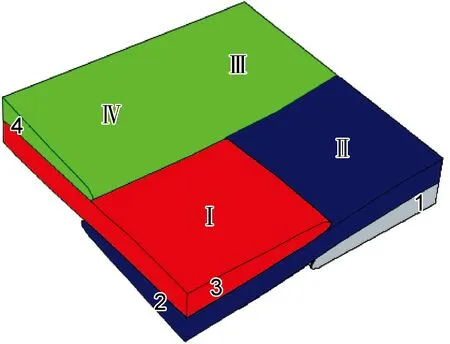
图2 交叉起伏区域细观结构Fig.2 Meso-scale structure of crossover and undulation region
以缠绕面为基准,将图2所示的交叉起伏区域看作是长方体结构,再用平行横截面分别将空间结构模型离散为M×N个子模型,如图3,4所示,红色、蓝色、绿色表示纤维束,黄色表示基体,此子模型就是用来描述缠绕复合材料交叉起伏区域的细观模型。 其中hf,up(mn),hf,down(mn)分别表示MN子模型中上下两层纤维束的厚度,hr,up(mn),hr,down(mn)分别表示MN子模型中上下两层基体的厚度,下标f,r分别表示纤维和树脂。
由于在交叉起伏区域纤维束截面形状发生改变,为了便于分析讨论,将交叉起伏细观模型分为Ⅰ,Ⅱ,Ⅲ,Ⅳ四个分区域(图2)。
用三角函数来描述交叉起伏区域纤维束的起伏路径:
(1)
式中:g(w)为纤维束中面的形状函数;a为单层纤维束的厚度;w为沿着起伏方向的距离;b为起伏区域的长度。
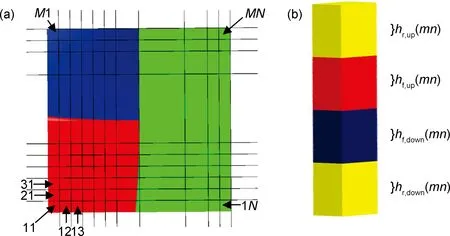
图3 子模型编号图(a)与MN子模型图(b)Fig.3 Picture of sub-cell number(a) and MN sub-cell(b)
其中的Ⅰ分区域,各个子模型基体以及纤维束含量可以由式(2)确定。
(2)
其他3个分区域,各个子模型的基体以及纤维束含量的计算方法相类似。
1.2固化过程中热传导和固化反应动力学方程
热固性树脂基复合材料的固化过程是热传导和固化反应相互耦合的物理化学问题,忽略树脂的流动以及热对流的影响,可以得到瞬态热传导控制方程和固化反应动力学方程[11]:
(3)
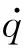
与固化进程相关的树脂弹性模量由式(4)来确定。
(4)
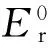
对树脂而言,热膨胀系数的取值可以根据树脂在固化过程中的3种不同状态分为3段:黏流态的热膨胀系数,橡胶态的热膨胀系数和玻璃态的热膨胀系数。
(5)
(6)
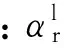
1.3树脂体积收缩模型
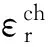
(7)
树脂的体积变化率ΔV与树脂完全固化时的体积收缩率有如下关系:
(8)
(9)
式中:Δc为几何因子;Vch为完全固化后总的体积变化率。
复合材料3个主方向的化学收缩应变可以通过式(10)[12]求得:
(10)
式中:ν为泊松比;Vf为纤维体积分数。
1.4固化过程应力应变关系
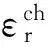
固化过程中树脂区应力应变关系为:
(11)
固化过程中纤维区应力应变关系为:
(12)
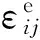
2 数值算例与讨论
基于上述计算模型,运用ABAQUS软件建立了缠绕复合材料交叉起伏区域几何模型。将交叉起伏区域看作长方体结构,再用平行截面将空间结构模型离散为M×N个子模型,每个子模型内含有两微段树脂基体以及两微段纤维束(图3)。微段树脂基体和微段纤维束在固化过程中的应力分别按照公式(11),(12)计算。再结合纤维缠绕复合材料在固化工艺中温度和固化度的变化规律,分析了交叉起伏区域残余应力分布和变化规律。模拟计算所用材料为碳纤维环氧树脂预浸料(AS4/3506-1),参考文献[13]确定材料性能参数和复合材料体系固化动力学参数。
2.1固化过程分析
为了清楚反映起伏区域不同位置处树脂的固化情况,分别取A,B,C 3个局部区域(C-外层树脂区,B-富树脂区,A-层合树脂区) 如图4(a)所示,这3个区域的固化曲线如4(b)所示。由于纤维层厚度较小,温度很快从外部传入内部,因此固化曲线基本一致,但是由于中心区域(富树脂区域)树脂含量大,固化反应放热量大,促进了固化反应进行,在第一个保温阶段和第二次升温阶段,固化速率稍微大于其他区域。整体上在第一个升温保温阶段,固化反应速率较慢,在t=4000s左右,固化完成30%;当固化进行到一定程度,树脂达到凝胶状态后,固化加速,在t=6000s左右,固化完成60%;在第二个升温阶段,固化速率加快,在t=11000s左右固化完成。
2.2残余应力分析
图7为固化过程中交叉起伏区域纤维束残余应力
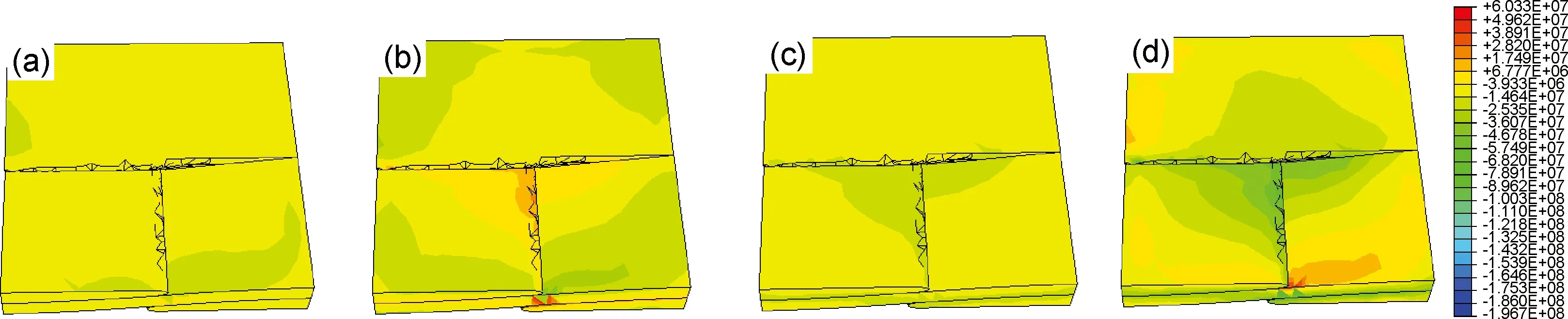
图5 交叉起伏区域纤维束残余应力变化历程 (a)t=4043s;(b)t=6168s;(c)t=12867s;(d)t=16538sFig.5 The changing course of residual stress in fiber bundle crossover and undulation region(a)t=4043s;(b)t=6168s;(c)t=12867s;(d)t=16538s
变化历程。初始阶段,残余应力主要是热传导引起的热膨胀的结果;中期阶段,残余应力随固化反应的进行而增大,在t=13000s左右富树脂区残余应力由拉应力状态向压应力状态转变,残余应力最大值出现在纤维束2,3内部边界起伏角度最大处,这是由于,一方面,在交叉起伏处纤维束相互挤压,出现应力集中,另一方面,在纤维束内侧附近树脂含量高,化学收缩变形严重,导致残余应力增大。
为了描述纤维起伏区域、层合区域以及富树脂区域在固化过程中残余应力的变化情况,在图6(a)的纤维束2上不同位置取H,I,J 3个局部区域(H-起伏区域,I-富树脂区域,J-层合区域),图6(b)为这3个区域残余应力变化情况。在固化过程开始阶段(0~4000s),树脂受热变软,呈黏流态,复合材料尚未达到凝胶态。在第一个升温阶段后期以及第二个升温保温阶段前期(4000~12000s),同时存在热膨胀引起的热应力和固化反应导致化学收缩引起的残余应力。在第二个升温保温阶段后期以及降温阶段(12000~18000s),固化反应逐渐结束,放热消失,随后主要是温度变化,纤维起伏区和富树脂区受温度影响更为明显,呈压应力状态。
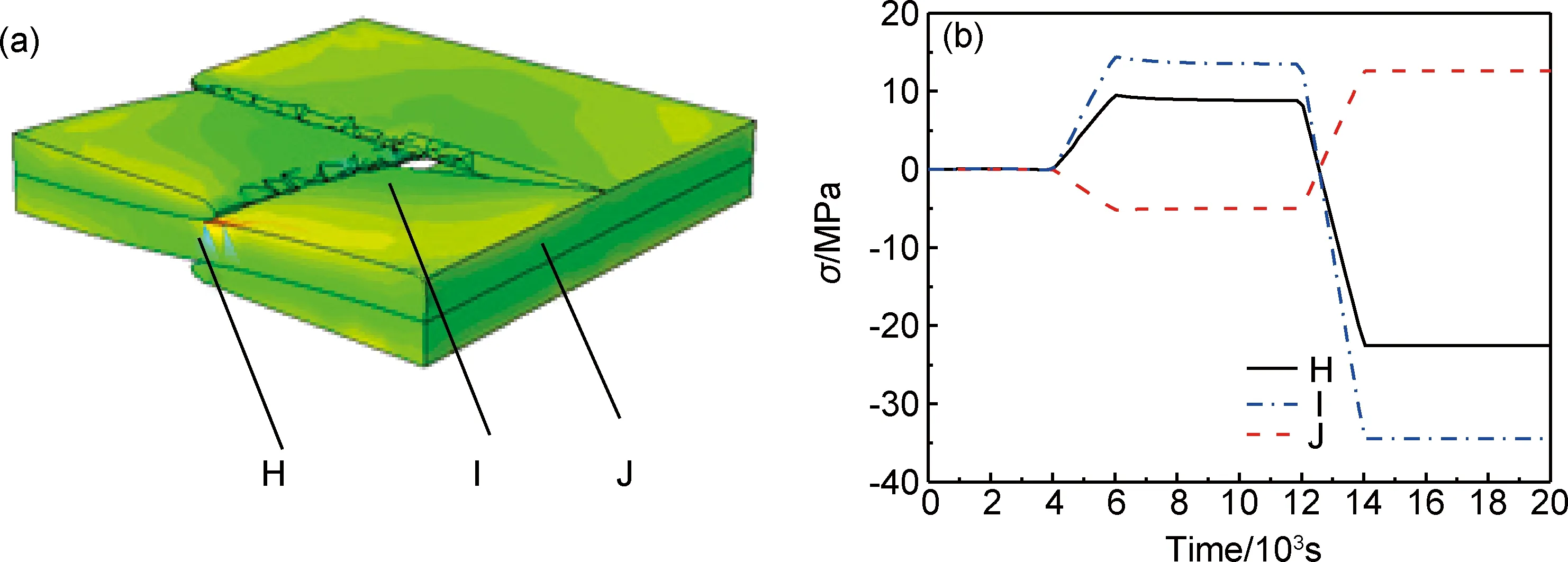
图6 纤维束2不同位置示意图(a)和残余应力曲线(b)Fig.6 Different positions of 2nd fiber bundle(d) and curves of residual stress(b)
图7为纤维束不同位置残余应力分布,沿图7(a)中箭头所示方向开始部分(位置1~3点)为层合区域,中间部分(位置4~11点)为起伏区域,最后部分(位置12~15点)是富树脂区域。由图7(b)可以看出层合区呈现拉应力状态,纤维束起伏区出现拉/压应力状态转换,富树脂区呈现最大压应力。
图7 纤维束不同位置示意图(a)和残余应力曲线(b)Fig.7 Different positions of fiber bundle(a) and curve of residual stress(b)
为了更好地分析残余应力在起伏区域的分布特性,图8给出了纤维束起伏段残余应力变化规律(位置1~3点为层合区域,位置4~13点为起伏区域,位置14~16点为层合区域),可以看出起伏段残余应力变化复杂,在纤维束上不同位置出现拉、压不同的应力状态,在起伏角度最大处(富树脂区域)出现最大压应力。这种情况发生的主要原因是起伏区域中纤维束呈空间非正交的复杂状态及树脂的不均匀分布,造成固化过程温度场变化复杂,同时影响固化过程中化学收缩效应,最终导致此处压应力最大。
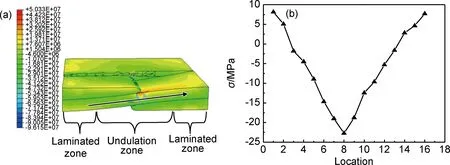
图8 纤维束起伏段残余应力变化图 (a)纤维束不同位置示意图;(b)残余应力曲线Fig.8 Variation of residual stress in fiber undulation region(a)different positions of fiber bundle;(b)curve of residual stress
3 结论
(1)针对纤维交叉起伏区域残余应力,建立了一种细观分析模型。基于热传导方程、固化反应动力学模型和复合材料层合理论,采用有限元方法对缠绕复合材料在固化工艺过程中的残余应力分布及其变化规律进行了数值模拟。
(2)纤维起伏区域包括层合区、起伏区和富树脂区3部分,不同部分的残余应力明显不同,在固化过程中均出现拉、压应力状态转换,最终层合区纤维束呈现拉应力状态,起伏区纤维束呈现压应力状态,富树脂区出现最大压应力。
(3)残余应力沿纤维束起伏方向呈现V型变化趋势,在纤维束上不同位置出现拉、压不同的应力状态,起伏角度最大处出现最大压应力。
[1]GOPAL A K,ADALI S,VERIJENKO V E. Optimal temperature profiles for minimum residual stress in the cure process of polymer composites[J]. Composite Structures,2000,48(1):99-106.
[2]TARSHA-KURIDI K E,OLIVIER P. Thermo-viscoelastic analysis of residual curing stresses and the influence of autoclave pressure on these stresses in carbon/epoxy laminates[J]. Composites Science & Technology,2002,62(4):559-565.
[3]ZHANG X C,XU B S,WANG H D,et al. Prediction of three-dimensional residual stresses in the multilayer coating-based systems with cylindrical geometry[J]. Composites Science & Technology,2006,66(13):2249-2256.
[4]YANG L,YAN Y,MA J,et al. Effects of inter-fiber spacing and thermal residual stress on transverse failure of fiber-reinforced polymer-matrix composites[J]. Computational Materials Science,2013,68(2):255-262.
[5]ZOBEIRY N,VAZIRI R,POURSARTIP A. Computationally efficient pseudo-viscoelastic models for evaluation of residual stresses in thermoset polymer composites during cure[J]. Composites Part A:Applied Science & Manufacturing,2010,41(2):247-256.
[6]赵玉萍,袁鸿,韩军,等. 基于内聚力模型的纤维复合材料残余应力分析[J]. 材料热处理学报,2014,(12):216-221.
ZHAO Y P,YUAN H,HAN J,et al. Analysis of residual stress in fiber reinforced composite using cohesive zone model[J].Transactions of Materials and Heat Treatment,2014,35(12):216-221.
[7]胡照会,王荣国,赫晓东,等. 复合材料层板固化全过程残余应变/应力的数值模拟[J]. 航空材料学报,2008,28(2):55-59.
HU Z H,WANG R G,HE X D,et al. Numerical simulation of residual strain/stress for composite laminate during overall curing process[J].Journal of Aeronautical Materials,2008,28(2): 55-59.
[8]王建花,钱林方,袁人枢. 复合材料身管的热残余应力[J]. 弹道学报,2007,19(1):82-85.
WANG J H,QIAN L F,YUAN R S. Thermal residual stresses in composite material barrel[J].Journal of Ballistics,2007,19(1): 82-85.
[9]黄其忠,任明法,陈浩然. 复合材料网格结构软模共固化成型工艺数值仿真[J]. 复合材料学报,2010,27(1):25-31.
HUANG Q Z,REN M F,CHEN H R. Numerical simulation of soft-mode aided co-curing process for advanced grid stiffen structure[J].Acta Materiae Compositae Sinica,2010,27(1):25-31.
[10]马豪,李岩,王迪,等. 固化温度对亚麻纤维及其增强复合材料力学性能的影响[J]. 材料工程,2015,43(10):14-19.
MA H,LI Y,WANG D,et al. Effect of curing temperature on mechanical properties of flax fiber and their reinforced composites[J].Journal of Materials Engineering,2015,43(10):14-19.
[11]郭章新,韩小平,李金强,等. 纤维缠绕复合材料固化过程残余应力/应变的三维数值模拟[J]. 复合材料学报,2014,31(4):1006-1012.
GUO Z X,HAN X P,LI J Q,et al. Three-dimensional numerical simulation of residual stress/strain for filament-wound composite during curing process[J]. Acta Materiae Compositae Sinica,2014,31(4):1006-1012.
[12]BOGETTI T A,GILLESPIE J W. Process-induced stress and deformation in thick-section thermoset composite laminates[J].Journal of Composite Materials,1992,26(5):626-660.
[13]LEE W I,LOOS A C,SPRINGER G S. Heat of reaction,degree of cure,and viscosity of Hercules 3501-6 resin[J]. Journal of Composite Materials,1982,16(6):510-520.
Residual Stresses in Local Fiber Undulations for Filament-wound Composites
HE Xin-hui1,2,HAN Xiao-ping1,2
(School of Mechanics, Civil Engineering and Architecture,Northwestern Polytechnical University,Xi’an 710129,China;2 State Key Laboratory for Strength and Vibration of Mechanical Structures,Xi’an Jiaotong University,Xi’an 710049,China)
Aimed at the fiber crossover and undulation, a meso-scale model was proposed to analyze the residual stress in the undulation regions of filament-wound composites. The process induced residual stress fields of filament-wound composites during curing process was numerically simulated by commerce software. Based on transit heat conductive equation, curing kinetics model and composite laminated stress analysis theories, the corresponding formulas of the finite element analysis were introduced. The time’s course and variation scope of residual stress during curing process were fully investigated through the example analysis. The results show that there is great difference of residual stress in different positions of fiber bundle. In laminated zone, the fiber bundle is under tensile stress state, while in fiber undulation zone, that is under compressive stress state, and the maximum residual stress appears in resin rich zone. The residual stress shows V-shaped trend along undulation direction, and it appears tensile or compressive stress state in different position of fiber bundle. The maximum compressive residual stress appears in the fiber maximize undulation angle.
filament-wound composite;curing process;residual stress;fiber bundle crossover and undulation;meso-scale model
2015-07-14;
2015-12-24
韩小平(1958-),男,博士,教授,主要从事复合材料及其结构的力学分析研究工作,联系地址:陕西省西安市西北工业大学长安校区力学与土木建筑学院883信箱(710129),E-mail:xphan@nwpu.edu.cn
10.11868/j.issn.1001-4381.2016.04.013
TB332
A
1001-4381(2016)04-0076-06

