通用EIV平差模型及其加权整体最小二乘估计

曾文宪，方　兴，刘经南,2，姚宜斌

1. 武汉大学测绘学院，湖北 武汉 430079； 2. 武汉大学卫星导航定位技术研究中心，湖北 武汉 430079



通用EIV平差模型及其加权整体最小二乘估计

曾文宪1，方兴1，刘经南1,2，姚宜斌1

1. 武汉大学测绘学院，湖北 武汉 430079； 2. 武汉大学卫星导航定位技术研究中心，湖北 武汉 430079

Foundationsupport：TheNationalNaturalScienceFoundationofChina(Nos. 41404005；41474006；41231174；41274022 );TheFundamentalResearchFoundsfortheCentralUniversities(No. 2042016kf0175)

以平差基本理论为基础，提出了EIV(errors-in-variables)平差模型的通用形式，涵盖了间接平差、条件平差、附有参数的条件平差及附有限制条件的间接平差等基本EIV模型形式。基于整体最小二乘估计准则，研究了通用EIV模型的加权整体最小二乘算法，并推导了估计结果的近似精度公式。通用EIV模型及其整体最小二乘算法是对EIV模型估计理论的进一步完善，统一的整体最小二乘算法有利于软件的编程实现，有助于推动EIV模型估计理论的应用。

通用EIV平差模型；加权整体最小二乘算法；估计精度;非线性最优化算法

经典平差模型的通用形式涵括了条件平差、附有参数的条件平差、间接平差及附有限制条件的间接平差等基本平差模型[1]。假定观测向量含随机误差，参数的系数矩阵为固定量，采用最小二乘估计(leastsquares，LS)准则可求得上述4类基本平差模型以及通用平差模型的最优无偏解。最小二乘估计理论是数据处理的基本方法之一，在大地测量等众多科学研究和工程领域应用广泛。

随着现代各专业领域对模型和数据精度要求的不断提高，当平差模型参数的系数矩阵包含随机误差(errors-in-variables，EIV)时，最小二乘估计有偏[2]。文献[3]首次将最小二乘估计准则扩展至整体最小二乘估计(totalleastsquares，TLS)，即同时顾及所有观测数据(观测向量和系数矩阵)的随机误差。文献[2]证明了EIV模型的TLS解具有渐进无偏性，理论上要优于LS解。假定权矩阵为对角阵的情况下，文献[4]通过线性化首次推导了统计意义上的加权整体最小二乘算法(weightedtotalleastsquares，WTLS)，文献[5]采用拉格朗日乘数法导出了WTLS解。之后，众多文献研究了系数矩阵与观测向量在特殊权矩阵情况下的WTLS算法[6-9]，文献[10—12]提出了仅限定系数矩阵和观测向量不相关情况下的WTLS算法，文献[13—15]将WTLS算法推广到任意权矩阵的一般情况。通过将模型扩展到附有限制条件的EIV模型，文献[16—22]研究了附有等式和不等式约束的WTLS算法。文献[23]在假定观测向量和系数矩阵误差不相关的情况下研究了EIV条件平差模型的WTLS算法。

到目前为止，WTLS算法主要基于EIV间接平差模型或者附有限制条件的间接平差模型，即参数的系数矩阵随机，观测向量的系数矩阵为单位阵。尽管间接平差模型是最常用的平差模型，但并非通用的平差模型形式，如观测向量的系数矩阵可能包含随机误差，因此，从平差模型理论而言，类似于经典平差模型发展脉络，EIV模型形式尚有待进一步完善。从应用上而言，某些特定数据在一定条件下或许更适宜于表示为条件平差或者附有参数的条件平差模型等形式，需要扩展相应的模型形式供选择和比较。基于上述理论和应用两方面的意义，本文提出了EIV平差模型的通用形式，包括观测向量的系数矩阵和参数的系数矩阵随机或者非随机等各类情况，在此基础上，采用拉格朗日乘数法推导了通用EIV平差模型的统一WTLS算法及其近似精度估计公式。通用EIV平差模型的WTLS算法适用于任意权矩阵，涵括了条件平差、附有参数的条件平差、间接平差以及附有限制条件的间接平差等各类模型形式，统一的WTLS算法有利于具体工程的编程实现。

1　通用EIV平差模型形式

1.1经典平差模型的通用形式及其最小二乘解

经典平差函数模型的通用形式为[1]

B(y+vy)+Ax+w=0

(1)

式中，y和vy表示n×1的观测向量和改正数向量；B为f×n观测向量系数矩阵；x为u×1参数向量；A为f×u的参数系数矩阵；w为f×1常数向量；B和A均为固定矩阵。

按照经典平差理论，模型(1)涵括了条件平差、附有参数的条件平差、间接平差和附有限制条件的间接平差模型等4种基本函数模型形式，参数的最小二乘估计及其精度为[1]

1.2通用EIV平差模型

若把经典通用平差模型(1)中观测向量的系数矩阵B和参数的系数矩阵A由固定矩阵推广到随机矩阵，从而经典平差模型扩展为通用EIV平差模型

(B+VB)(y+vy)+(A+VA)x+w=0

(2)

式中，y和vy表示n×1的观测向量及其改正数向量；B和VB表示f×n的观测向量系数矩阵及其改正数矩阵；x为u×1参数向量；A和VA表示f×u的参数系数矩阵及其改正数矩阵。B、y和A为含随机误差的观测数据，模型(2)的随机模型可表示为

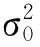
通用EIV模型(2)涵括了以下4种基本EIV平差模型：

(1) 当模型不含参数x，仅由观测值y的几何关系构成条件方程，称为EIV条件平差模型

(B+VB)(y+vy)+w=0

(3)

(2) 当模型中含有部分参数时，观测值和参数共同构成条件方程，称为EIV附有参数的条件平差模型，模型形式与式(2)等同。

(3) 当y能够表示为独立参数x的函数，即表示成观测方程的形式，称为EIV间接平差模型

y+vy=(A+VA)x+w

(4)

(4) 当参数x间存在函数关系时，称为EIV附有限制条件的间接平差模型

Bc(y+vy)+(Ac+VAc)x+wc=0

(5)

2　通用EIV平差模型的加权整体最小二乘估计

2.1WTLS算法

整体最小二乘准则本质上是最小二乘准则的扩展，要求系数矩阵和观测向量中的全部观测数据L的残差平方和最小，该准则下模型(2)的求解转化为以下最优化估计问题

相应的目标函数为

Φ(v,λ,x)=vTPv+2λT(By+Bvy+VBy+VBvy+Ax+VAx+w)=

vTPv+2λT(By+Ax+Cv+w)

将上式分别对待估计量求一阶偏导并令其等于0

(6)

(7)

(8)

式中，变量上加尖号表示模型的估计量。

由式(7)得

(9)

式(9)代入式(8)

(10)

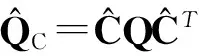
式(10)代入式(9)

(11)

式(10)代入式(6)得到WTLS参数解

(12)

(13)

2.2WTLS估计结果的精度评定

由于EIV模型的非线性特点，到目前为止，WTLS解的统计特性研究成果非常有限[24]。文献[6,25—26]推导了等权情况下的精度近似公式。文献[10,27]通过将EIV模型转化为经典平差模型研究了WTLS解的一阶近似精度。本文对通用EIV模型进行线性化，将其转换为线性高斯赫尔默特模型形式，推导了一阶近似精度公式。

参数或随机量符号上加“～”表示真值，模型(2)可写为如下形式

则模型(2)的线性化形式可表示为

A0Δx+Clvl+wl=0

(14)

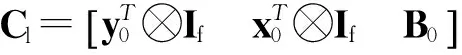
(15)

(16)

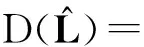
(17)

3　实例分析

本节以直线拟合模型为例说明和验证论文提出的模型和算法。尽管对于直线拟合而言，采用EIV间接模型更为简单直观，但随着EIV模型在现代测绘领域应用的深入，某些模型可能更适用于其他EIV模型形式，因此，为了说明通用EIV模型及其WTLS算法的估计过程，实例将直线表示为通用EIV模型(2)的形式，即附有参数的条件平差模型形式进行估计。

若设直线的截距和斜率为待估参数，直线的EIV间接平差模型形式(4)为

(18)

表1　直线数据点的观测值

若仅设斜率为参数x，直线的EIV间接形式(18)转化为通用EIV模型(2)的形式，其中多余观测数为2，参数个数为1，则3个线性无关的条件方程为

(19)

式中，第1式描述了过1、3两点的直线斜率等于过1、2两点直线的斜率，第2、3式描述了根据第1点计算的截距分别等于第2、第4点计算的截距，上式写成矩阵形式为

(20)

表2　通用EIV平差模型估计结果

分析EIV模型(18)的估计结果，可得到如下结论：

(1) 表2计算结果表明，通用EIV模型的WTLS算法与目前EIV间接模型的WTLS常规算法结果相等，证明了本文算法的正确性。 此外，通用WTLS估计精度公式与间接WTLS精度公式均为估计参数的一阶近似精度公式，两者仅模型形式不同，因此两种算法参数的估计精度相等。

(2) 如果将式(19)第一个条件方程改为第1点计算的截距等于第3点的截距，此时，条件方程简化为仅A为随机矩阵而B为固定矩阵的EIV附有参数的条件平差模型：B(y+vy)+(A+VA)x+w=0。

(3) 若不设任何参数，利用直线方程的两点式可列出直线拟合的EIV条件平差模型：(B+VB)(y+vy)+w=0。

(4) 如果某个观测点i视为无误差的已知点，可列出EIV附有限制条件的间接平差模型

从以上实例分析可以看到，对于某个具体EIV平差问题，可以根据需要选择适宜的平差模型形式求解。通用EIV模型涵括了EIV的4类基本平差模型形式，本文提出的WTLS算法是4种模型的统一解。

[1]武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉: 武汉大学出版社, 2003.

TheGroupofSurveyingAdjustmentintheSchoolofGeodesyandGeomatics,WuhanUniversity.ErrorTheoryandFoundationofSurveyingAdjustment[M].Wuhan:WuhanUniversityPress, 2003.

[2]VANHUFFELS,VANDEWALLEJ.TheTotalLeastSquaresProblem:ComputationalAspectsandAnalysis[M].Philadelphia:SocietyforIndustrialandAppliedMathematics, 1991.

[3]ADCOCKRJ.NoteontheMethodofLeastSquares[J].TheAnalyst, 1877, 4(6): 183-184.

[4]DEMINGWE.TheApplicationofLeastSquares[J].TheLondon,Edinburgh,andDublinPhilosophicalMagazineandJournalofScience:Series7, 1931, 11(68): 146-158.

[5]GERHOLDGA.Least-squaresAdjustmentofWeightedDatatoaGeneralLinearEquation[J].AmericanJournalofPhysics, 1969, 37(2): 156-161.

[6]SCHAFFRINB,WIESERA.OnWeightedTotalLeast-squaresAdjustmentforLinearRegression[J].JournalofGeodesy, 2008, 82(7): 415-421.

[7]陈义, 陆珏. 以三维坐标转换为例解算稳健总体最小二乘方法[J]. 测绘学报, 2012, 41(5): 715-722.

CHENYi,LUJue.Performing3DSimilarityTransformationbyRobustTotalLeastSquares[J].ActaGeodaeticaetCartographicaSinica, 2012, 41(5): 715-722.

[8]LIBofeng,SHENYunzhong,ZHANGXingfuetal.SeamlessMultivariateAffineError-in-variablesTransformationandItsApplicationtoMapRectification[J].InternationalJournalofGeographicalInformationScience, 2013, 27(8): 1572-1592.

[9]王乐洋. 地壳应变参数反演的总体最小二乘方法[J]. 大地测量与地球动力学, 2013, 33(3): 106-110.

WANGLeyang.InversionofCrustalStrainParametersBasedonTotalLeastSquares[J].JournalofGeodesyandGeodynamics, 2013, 33(3): 106-110.

[10]XUPeiliang,LIUJingnan,SHIChuang.TotalLeastSquaresAdjustmentinPartialErrors-in-variablesModels:AlgorithmandStatisticalAnalysis[J].JournalofGeodesy, 2012, 86(8): 661-675.

[11]SHENYunzhong,LIBofeng,CHENYi.AnIterativeSolutionofWeightedTotalLeast-squaresAdjustment[J].JournalofGeodesy, 2010, 85(4): 229-238.

[12]姚宜斌, 孔建. 顾及设计矩阵随机误差的最小二乘组合新解法[J]. 武汉大学学报(信息科学版), 2014, 39(9): 1028-1032.

YAOYibin,KONGJian.ANewCombinedLSMethodConsideringRandomErrorsofDesignMatrix[J].GeomaticsandInformationScienceofWuhanUniversity, 2014, 39(9): 1028-1032.

[13]FANGXing.WeightedTotalLeastSquares:NecessaryandSufficientConditions,FixedandRandomParameters[J].JournalofGeodesy, 2013, 87(8): 733-749.

[14]方兴, 曾文宪, 刘经南, 等. 三维坐标转换的通用整体最小二乘算法[J]. 测绘学报, 2014, 43(11): 1139-1143.DOI:10.13485/j.cnki.11-2089.2014.0193.

FANGXing,ZENGWenxian,LIUJingnan,etal.AGeneralTotalLeastSquaresAlgorithmforThree-dimensionalCoordinateTransformations[J].ActaGeodaeticaetCartographicaSinica, 2014, 43(11): 1139-1143.DOI:10.13485/j.cnki.11-2089.2014.0193.

[15]FANGXing.ATotalLeastSquaresSolutionforGeodeticDatumTransformations[J].ActaGeodaeticaetGeophysica, 2014, 49(2): 189-207.

[16]SCHAFFRINB,FELUSYA.OnTotalLeast-squaresAdjustmentwithConstraints[C]∥ProceedingsoftheInternationalAssociationofGeodesyIAGGeneralAssemblySapporo.Berlin:Springer, 2005, 128: 417-421.

[17]MAHBOUBV,SHARIFIMA.OnWeightedTotalLeast-squareswithLinearandQuadraticConstraints[J].JournalofGeodesy, 2013, 87(3): 279-286.

[18]ZENGWenxian,LIUJingnan,YaoYibin.OnPartialErrors-in-variablesModelswithInequalityConstraintsofParametersandVariables[J].JournalofGeodesy, 2015, 89(2): 111-119.

[19]曾文宪, 方兴, 刘经南, 等. 附有不等式约束的加权整体最小二乘算法[J]. 测绘学报, 2014, 43(10): 1013-1018.DOI:10.13485/j.cnki.11-2089.2014.0173.

ZENGWenxian,FANGXing,LIUJingnan,etal.WeightedTotalLeastSquaresAlgorithmwithInequalityConstraints[J].ActaGeodaeticaetCartographicaSinica, 2014, 43(10): 1013-1018.DOI:10.13485/j.cnki.11-2089.2014.0173.

[20]FANGXing.AStructuredandConstrainedTotalLeast-squaresSolutionwithCross-covariances[J].StudiaGeophysicaetGeodaetica, 2014, 58(1): 1-16.

[21]FANGXing.OnNon-combinatorialWeightedTotalLeastSquareswithInequalityConstraints[J].JournalofGeodesy, 2014, 88(8): 805-816.

[22]FANGXing.WeightedTotalLeast-squareswithConstraints:AUniversalFormulaforGeodeticSymmetricalTransformations[J].JournalofGeodesy, 2015, 89(5): 459-469.

[23]TONGXiaohua,JINYanmin,ZHANGSonglin,etal.Bias-correctedWeightedTotalLeast-squaresAdjustmentofConditionEquations[J].JournalofSurveyingEngineering, 2014, 141(2).DOI: 10.1061/(ASCE)SU.1943-5428.0000140.

[24]刘经南, 曾文宪, 徐培亮. 整体最小二乘估计的研究进展[J]. 武汉大学学报(信息科学版), 2013, 38(5): 505-512.

LIUJingnan,ZENGWenxian,XUPeiliang.OverviewofTotalLeastSquaresMethods[J].GeomaticsandInformationScienceofWuhanUniversity, 2013, 38(5): 505-512.

[25]GLESERLJ.EstimationinaMultivariate“ErrorsinVariables”RegressionModel:LargeSampleResults[J].TheAnnalsofStatistics, 1981, 9(1): 24-44.

[26]许超钤, 姚宜斌, 张豹, 等. 基于整体最小二乘的参数估计新方法及精度评定[J]. 测绘通报, 2011(10): 1-4.

XUChaoqian,YAOYibin,ZHANGBao,etal.NewMethodofParametersEstimationandAccuracyEvaluationBasedonTLS[J].BulletinofSurveyingandMapping, 2011(10): 1-4.

[27]孔建, 姚宜斌, 黄承猛. 非线性模型的一阶偏导数确定方法及其在TLS精度评定中的应用[J]. 大地测量与地球动力学, 2011, 31(3): 110-114.

KONGJian,YAOYibin,HUANGChengmeng.MethodforDeterminingFirst-orderPartialDerivativeofNonlinearModelandItsApplicationinTLSAccuracyAssessment[J].JournalofGeodesyandGeodynamics, 2011, 31(3): 110-114.

(责任编辑：宋启凡)

修回日期： 2016-06-10

E-mail：wxzeng@sgg.whu.edu.cn

Correspondingauthor：FANGXing

E-mail：xfang@sgg.whu.edu.cn

WeightedTotalLeastSquaresofUniversalEIVAdjustmentModel

ZENGWenxian1,FANGXing1,LIUJingnan1,2,YAOYibin1

1.SchoolofGeodesyandGeomatics,WuhanUniversity,Wuhan430079,China; 2.ResearchCenterofGNSS,WuhanUniversity,Wuhan430079,China

Thispaperproposestheuniversalerrors-in-variables(EIV)adjustmentmodelbasedonthefundamentaladjustmenttheory,whichcoverstheparametricadjustmentmodel,conditionaladjustmentmodel，conditionaladjustmentmodelwithparametersandparametricadjustmentmodelwithconstrains.Applyingtotalleastsquares(TLS)principle,wededucetheweightedTLS(WTLS)algorithmandtheapproximatedprecisionoftheEIVmodel.TheuniversalEIVadjustmentmodelanditsestimatorofWTLScontributetotheintegrityoftheoryofEIVmodelestimation.TheproposeduniformWTLSalgorithmisappropriateforprogramminginsoftware,whichcancontributetothegeodeticapplicationofthetheoryoftheEIVmodelestimation.

universalEIVadjustmentmodel;weightedtotalleastsquares;precision;nonlinearoptimization

ZENGWenxian(1975—),female,PhD,majorsinthetheoryandmethodofsurveyingdataprocessing.

P207

A

1001-1595(2016)08-0890-05

国家自然科学基金(41404005；41474006；41231174；41274022)；中央高校基本科研基金(2042016kf0175)

2015-03-25

曾文宪(1975—)，女，博士，主要从事测量数据处理理论与应用的研究。

方兴

引文格式：曾文宪，方兴，刘经南，等.通用EIV平差模型及其加权整体最小二乘估计[J].测绘学报，2016,45(8)：890-894.DOI:10.11947/j.AGCS.2016.20150156.

ZENGWenxian,FANGXing,LIUJingnan,etal.WeightedTotalLeastSquaresofUniversalEIVAdjustmentModel[J].ActaGeodaeticaetCartographicaSinica,2016,45(8):890-894.DOI:10.11947/j.AGCS.2016.20150156.