GPS民用广播星历中ISC参数精度分析及其对导航定位的影响

王宁波，袁运斌，张宝成，李子申

1. 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室，湖北 武汉 430077； 2. 中国科学院光电研究院，北京 100094； 3. 中国科学院大学，北京 100049



GPS民用广播星历中ISC参数精度分析及其对导航定位的影响

王宁波1, 3，袁运斌1，张宝成1，李子申2

1. 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室，湖北 武汉 430077； 2. 中国科学院光电研究院，北京 100094； 3. 中国科学院大学，北京 100049

Foundationsupport：TheNationalNaturalScienceFoundationofChina(Nos.41231064；41304034；41574033；41321063);TheBeijingNaturalScienceFoundation(No. 4144094)

2005年起发射的GPSBlockIIR-M卫星在L2频率上新增了L2C民用信号，2010年起发射的BlockIIF卫星新增了L5频率及L5I、L5Q两种民用信号。为此，GPS民用广播星历在原有时间群延迟(TGD)参数的基础上，新增了ISCC/A、ISCL2C、ISCL5I及ISCL5Q4种ISC(inter-signalcorrection)参数，以服务GPS实时导航定位用户。本文给出了ISC参数在GPS单/双频定位中的改正方法、利用不同机构提供的后处理差分码偏差(DCB)产品评估了ISC参数的实际精度、研究了ISC参数对GPS民用导航定位精度的影响。在明确TGD、ISC和DCB3类参数之间区别与联系的基础上，本文研究表明：GPS广播的ISCC/A参数精度可达0.2ns，TGD、ISCL2C及ISCL5Q参数精度可达0.5ns；以2014年连续11d全球12个MGEX(multi-GNSSexperiment)站为例，经由ISC参数改正后，GPSL2C单频标准单点定位(SPP)的位置解精度提高了30.6%，L1C/A+L2C双频SPP的位置解精度提高了12.2%，该精度与L1P(Y)+L2P(Y)消电离层组合SPP的位置解精度相当。

ISC参数；TGD参数；DCB参数；导航定位

不同类型的导航信号在卫星和接收机不同通道产生的时间延迟(或硬件延迟)并不完全一致，由此产生的两类导航信号之间的时延差异称为差分码偏差(differentialcodebias,DCB)[1]。其中，同一频率不同类型测距信号之间的DCB称为频内偏差，不同频率不同类型测距信号之间的DCB称为频间偏差[2-3]。卫星和接收机DCB是GNSS(globalnavigationsatellitesystem)电离层总电子含量(totalelectroncontent,TEC)计算必须扣除的误差[4-8]。同时，由于GNSS卫星钟差参数基准通常定义在某一个指定观测量(如BDSB3I)或某两个频率的消电离层组合观测量(如GPS(P1+P2)与Galileo(E1+E5a))上，使用不同于钟差参数基准的观测量时，需引入DCB参数进行卫星硬件时延偏差改正[9]。

常用的DCB产品可以为两类：一类是IGS(InternationalGNSSService)提供的高精度后处理产品，另一类是GNSS广播星历实时播发的时间群延迟(timinggroupdelay,TGD)或广播群延迟(broadcastgroupdelay,BGD)参数。IGS提供DCB产品的机构包括以欧洲定轨中心(CODE)为代表的电离层工作组和以德国宇航中心(DLR)为代表的MGEX(multi-GNSSexperiment)工作组[10-11]。CODE基于全球分布的IGS基准站采用电离层TEC建模的方式同步处理得到GPS及GLONASS的DCB参数，而DLR基于MGEX观测数据直接采用全球电离层格网(globalionosphericmap,GIM)扣除电离层TEC影响，进而估计得到GPS、GLONASS、BDS及Galileo的DCB参数[3, 12]。GPS、BDS及Galileo广播星历中均播发TGD参数，但各导航系统TGD参数的含义并不相同。BDS播发的TGD参数(包括TGD1和TGD2)本质上是B1B3和B1B2频点间的DCB参数，而GPS播发的TGD参数和Galileo播发的BGD(包括BGDE1,E5a和BGDE1,E5b)参数与DCB之间存在一个与频率有关的转换因子[13-14]。与IGS提供的DCB产品相比，TGD参数精度不高且更新频次较低(如GPSTGD参数平均每4个月更新一次[15])。但由于TGD参数能够通过广播星历实时获取，因而能够满足GNSS单/双频导航用户定位的DCB改正需求。

随着GPS的现代化，2005年起发射的GPSBlockIIR-M卫星在L2频率上增加了L2C民用信号，2010年起发射的GPSBlockIIF卫星新增了L5频率以及L5I5、L5Q5两种民用信号[16]。GPS广播星历的卫星钟差参数以L1P(Y)和L2P(Y)消电离层组合为参考基准，因此单独或联合采用4种民用信号(包括L1C/A、L2C、L5I5及L5Q5)实施标准单点定位(standardpointpositioning,SPP)时，需要将DCB作为一类改正信息。对GPS导航用户而言，除已有的TGD参数外，民用导航(civilnavigation,CNAV)星历中新增了4种ISC(inter-signalcorrection)参数。目前针对ISC参数使用方法、精度分析及其对GPS导航定位影响的研究较少，文献[17]介绍了ISC参数的使用方法，文献[18]基于CODE及DLR提供的DCB产品初步分析了ISC参数的精度。本文在文献[18]研究的基础上，首先给出并讨论了ISC参数的含义及其在GPS导航定位中的使用方法，进而利用不同机构提供的后处理DCB产品评估了ISC参数的实际精度，最后基于MGEX部分监测站观测数据分析了ISC参数对GPS导航用户单/双频定位精度的影响。

1　GPS ISC参数含义

GPS在L1C/A、L2C、L5I5及L5Q5民用信号上相对于L1P(Y)分别定义了一个ISC参数，即ISCC/A、ISCL2C、ISCL5I及ISCL5Q。GPS卫星TGD及ISC参数的定义如下[19]

(1)

表1进一步给出了GPS广播的TGD、ISC参数与后处理DCB参数之间的对应关系。表中第1列是民用导航星历中定义的TGD及ISC参数类型，第2列是RINEX3测码数据对应的DCB类型。目前MGEX试验网能够跟踪到C2L、C2S及C2X3种L2C类型码观测信号，而ISCL2C参数定义并未指定具体的码观测类型，使用时可将ISCL2C参数对应为DCBC1W-C2L、DCBC1W-C2S或DCBC1W-C2X中的任意一种。需要说明的是，第2列中给出的某些DCB类型在实际中无法直接得到，这是因为某些类型的GPS接收机无法同时观测到对应的两类测码信号。如TrimbleNETR9接收机只能同时输出C1C、C2W、C2X及C5X4种码观测量，而LeicaGR10/25接收机只能同时输出C1C、C2W、C2S及C5Q4种码观测量。第3列对应的是中国科学院测量与地球物理研究所(IGG)及DLR基于MGEX观测数据获得的DCB参数，不同于DLR直接采用GIM扣除电离层的影响[3]，IGG采用“两步法”逐测站处理得到卫星和接收机的DCB参数[20-21]。第4列对应的是CODE基于IGS全球基准站数据处理得到的DCB参数。分析结果表明，IGG、DLR、CODE提供的GPS卫星DCB产品精度分别可达0.15ns、0.2ns及0.1ns[3,12,20-21]。为便于后续对比分析，ISCL2C(对应DCBC1W-C2L或DCBP1-C2)和ISCL5Q(对应DCBC1W-C5Q)参数由不同机构DCB产品的线性组合得到。目前尚无GPS民用接收机能够观测到C5I信号，因此未给出ISCL5I参数实际对应的DCB产品类型。

表1GPS广播的TGD、ISC参数与DCB参数的对应关系

Tab.1GPS broadcast TGD and ISC parameters and their relation with DCBs

CNAVDCBIGG/DLRCODETGD-f22f21-f22·DCBC1W-C2W-f22f21-f22·DCBC1W-C2W-f22f21-f22·DCBP1-P2ISCL1C/ADCBC1W-C1C-DCBC1W-C1CDCBP1-C1ISCL2CDCBC1W-C2(L/S/X)DCBC1W-C2W-DCBC2W-C2LDCBP1-P2+DCBP2-C2ISCL5IDCBC1W-C5IISCL5QDCBC1W-C5Q-DCBC1C-C1W+DCBC1C-C5Q

2　GPS ISC参数改正模型

GPS广播星历中的钟差参数以L1P(Y)+L2P(Y)消电离层组合为参考基准，利用L1(Y)和L2P(Y)实施单点定位时，无需进行TGD参数改正[19]。然而，单独或联合采用L1C/A、L2C、L5I5及L5Q5信号进行单点定位时，需将TGD及ISC参数作为改正信息。本节给出了ISC参数在GPS单/双频导航定位中的改正方法。

GPS卫星与接收机视线方向的伪距观测方程可表示为

(2)

GPS卫星钟差是由L1P(Y)+L2P(Y)消电离层组合计算得到，因此，广播星历的卫星钟差参数ΔtSV中含有卫星端L1P(Y)和L2P(Y)的硬件延迟影响

(3)

由式(1)中TGD及ISC参数定义可知

(4)

式中，ISCLi,x为Li,x测码信号上定义的ISC参数。由式(3)、式(4)可进一步得到

Δts-τLi,x=ΔtSV-TGD+ISCLi,x

(5)

忽略观测噪声的影响，由式(2)、式(5)可以得到新的伪距观测方程

(6)

(7)

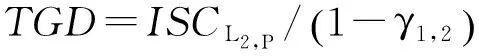
PC(L1,P(Y),L2,P(Y))=ρlos+c·Δtr-c·ΔtSV+T

(8)

GPS民用导航用户可根据式(6)改正TGD及ISC误差后进行单频单点定位，也可根据式(7)选择两种观测量进行双频消电离层组合定位。

3　GPS ISC参数精度分析

与TGD参数类似，GPS广播的ISC参数并非每天更新，而是以一定的时间间隔进行更新。本节首先对各GPS卫星ISC参数的更新频次及参数变化进行分析，在此基础上，利用不同机构提供的后处理DCB产品评估GPSISC参数的实际精度。明确ISC参数的变化规律及其实际精度有利于进一步分析其对GPS导航定位的影响。

选取2014年年积日(dayofyear,DOY)118d至2015年112dGPS民用导航星历的TGD及ISC参数， 分析GPS广播的TGD及ISC参数

的更新频次及其变化情况。图1给出了TGD及ISC参数在该时段内的更新时间示意，图中横坐标为GPS卫星SVN(spacevehiclenumber)号，括号内为PRN(pseudo-randomnoise)号，纵坐标为时间，不同颜色表示TGD或ISC参数的有效时间范围。可以看出，TGD参数并非严格地每4个月更新一次。SVN57、58、63及64号卫星的TGD参数在近一年的时间内都未更新(后文中的卫星号均指SVN号)；48、52及53号卫星的TGD参数2014年10月更新一次后便再未更新；66号卫星的TGD参数2014年10月更新一次后，2015年1月又更新了一次。比较而言，ISC参数的更新频次更有规律：各卫星的ISCC/A、ISCL2C及ISCL5Q参数在2014年6月及2015年2月分别更新了一次。从GPS导航定位对卫星硬件时延偏差的改正需求来看，广播的TGD及ISC参数最好一个月左右更新一次；然而受主控站数据处理策略等因素的影响，TGD及ISC参数可能几个月才更新一次。文献[22]的分析结果表明，由于卫星硬件时延参数稳定性较好，TGD参数数月更新一次能够保持较高的可靠性，但一年或更长时间更新一次则会引入较大的误差[23]。

图2给出了2014年DOY118—365天各GPS卫星TGD、ISC参数的变化情况，从上到下4幅子图分别对应TGD、ISCC/A、ISCL2C及ISCL5Q参数，图中竖线左边为GPSBlockIIR-M卫星，右边为BlockIIF卫星。从图中可以看出：①BlockIIR-M与BlockIIF卫星TGD参数差异约为20ns，相同类型卫星TGD之间的差异约为6ns。②BlockIIR-M卫星各ISCL2C参数之间的差异小于2ns，BlockIIF卫星ISCL2C参数的差异小于4ns，两类卫星ISCL2C参数差异约为13ns，小于不同类型卫星TGD参数之间的差异。③只有新发射的BlockIIF卫星能够播发ISCL5Q参数，各卫星ISCL5Q参数之间的差异最大可达6ns。④与TGD、ISCL2C及ISCL5Q参数相比，ISCC/A参数的变化范围最小：BlockIIR-M卫星ISCC/A参数之间的差异小于0.6ns，BlockIIF卫星的差异小于2.5ns。总体而言，不同类型卫星TGD、ISC参数差异较大，同一类型卫星TGD、ISC参数差异较小，同时，各卫星ISCC/A参数变化范围明显小于TGD、ISCL2C及ISCL5Q参数。

图1　GPS广播的TGD及ISC参数更新时间示意Fig.1　GPS broadcast TGD and ISC parameters update time interval

利用IGG、DLR及CODE提供的DCB产品评估GPS广播的TGD及ISC参数精度有以下两点原因：①DCB参数解算时利用了较多的全球基准站观测数据，其精度与可靠性高于广播星历中播发的TGD及ISC参数[14]。②IGG、DLR及CODE提供的DCB产品采用不同处理方法，基本反映了当前DCB参数的最高处理水平[3,12,21]。DCB、TGD及ISC参数解算时，卫星和接收机偏差参数是相关的，因此必须引入一个参考基准，才能实现卫星与接收机偏差参数的分离[20]。不同机构提供的DCB产品采用“零均值”基准约束，即所有卫星的DCB之和为零；而TGD及ISC参数采用某台硬件时延偏差标定的接收机为参考基准[3,21]。由于TGD、ISC参数与各机构DCB产品之间采用的参考基准不同，使用时需将不同的参考基准转换至统一的基准后再进行比较。假设有μ颗卫星，对所有卫星施加“零基准”约束，则有

(9)

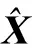
图2　不同GPS卫星的TGD及ISC参数值Fig.2　GPS broadcast TGD and ISC values of each individual satellite

选取其中μ1颗卫星构造新的卫星“零基准”约束

(10)

(11)

以GPS Block IIF卫星为参考构造新的卫星“零基准”约束，将GPS广播的TGD、ISC参数及后处理DCB参数转换至统一的卫星基准。图 3给出了各GPS卫星TGD、ISC参数相对于IGG、DLR及CODE 后处理DCB产品的平均偏差及STD，左上至右下4幅子图分别对应TGD、ISCC/A、ISCL2C及ISCL5Q参数。从图中可以看出，TGD参数与CODE产品之间的偏差为-0.31～0.30 ns，与IGG/DLR产品之间的偏差为-0.97～1.03 ns，与各机构DCB产品之间差异的STD为0.10～0.25 ns。ISCL2C参数与DLR产品之间的偏差较大(-1.32～0.86 ns)，与IGG及CODE产品之间的偏差基本相当(-1.16～0.49 ns)。目前CODE尚未提供与ISCL5Q对应的DCB产品，因此仅将ISCL5Q与IGG、DLR产品进行比较。除67号星外，ISCL5Q参数与IGG/DLR产品之间的偏差为-0.89～0.92 ns，STD为0.08～0.21 ns。ISCC/A参数与IGG/DLR产品之间的偏差较小，为-0.13～0.33 ns；与CODE产品之间的偏差为-0.53～0.31 ns。这种差异与IGG、DLR及CODE频内偏差参数的处理策略不同有关：IGG与DLR通过观测值的直接组合处理得到DCBC1C-C1W参数[3,21]，而CODE的DCBP1-C1参数是卫星钟差解算得到的副产品[12]。

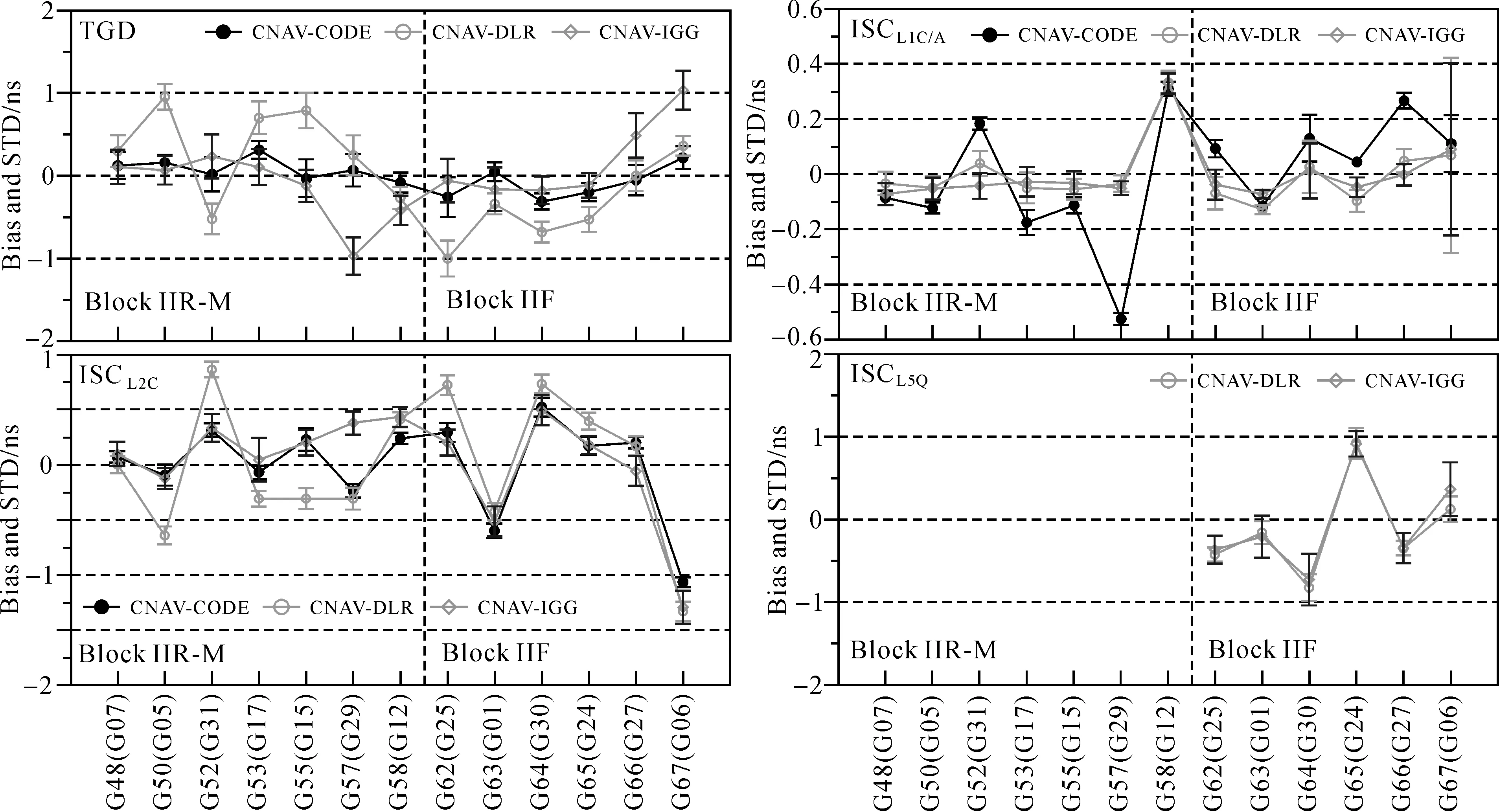
图3　GPS广播的TGD、ISC参数相对于IGG、DLR及CODE后处理DCB产品的平均偏差及STDFig.3　Bias and STD of the GPS broadcast TGD and ISCs relative to the DCB products of IGG, DLR and CODE

表2给出了GPS 广播的TGD及ISC参数的精度统计情况。表中第2列是各参数的变化范围，后3列是TGD、ISC参数相对于IGG、DLR及CODE 对应DCB产品偏差的RMS。从表中可以看出，TGD及ISC参数与不同机构DCB产品的比较结果略有差异；但总体而言，ISCC/A参数精度可以达到0.2 ns，TGD、ISCL2C及ISCL5Q参数精度能够达到0.5 ns。

表2GPS广播的TGD及ISC参数精度统计

Tab.2ConsistencyoftheGPSbroadcastTGDandISCsrelativetothatofIGG,DLRandCODE

ns

4　GPS ISC参数对单点定位影响分析

从式(6)可以看出，GPS民用导航信号伪距观测方程需同时引入TGD及ISC参数作为改正信息。为分析TGD、ISC参数在定位中的误差项大小，图 4给出了各GPS卫星TGD与ISCC/A、ISCL2C及ISCL5Q参数之间的差异。可以看出，GPSBlockIIR-M和BlockIIF卫星的TGD与ISCL2C参数之间的差异约为25ns，与ISCC/A参数的差异约为15ns。不同类型卫星TGD与ISC参数之间的差异较大，因此这些参数对定位的影响不能忽略。同时可以看出，GPSBlockIIR-M卫星TGD与ISCL2C、ISCC/A参数之间的差异分别为5ns、 2ns，BlockIIF卫星TGD与ISCL2C、ISCC/A及ISCL5Q参数之间的差异分别为6ns、4ns及7ns。同一类型卫星TGD与ISC参数之间的差异较小，仅采用GPSBlockIIR-M或BlockIIF卫星进行定位时，TGD及ISC参数对单点定位解的影响将会变小，这是因为各卫星相同的卫星硬件延迟误差在定位中会被接收机钟差参数吸收。

图4　不同GPS卫星TGD与ISCC/A、ISCL2C及ISCL5Q参数之间的差异Fig.4　Differences of ISCC/A, ISCL2C and ISCL5Q with respect to TGD parameters

由于各监测站能够同时观测到的GPS卫星数量有限，将不再单独利用GPSBlockIIR-M或BlockIIF卫星进行定位试验。同时，由于能够播发L5Q信号的GPS卫星较少，后续分析中将分别以GPSC2L及C1C+C2L观测量为例，分析ISC参数对GPS单/双频用户导航定位解的影响。

4.1试验方案

选取2014年连续11d(DOY300—310)12个MGEX站观测数据、采用单频SPP及双频消电离层组合SPP分析ISC参数对GPS民用导航用户定位精度的影响。试验期间电离层活动较为剧烈：太阳活动指数F10.7在120～188sfu之间变化，第300及308天的Kp指数大于4。MGEX测试站分布如图 5所示，接收机类型为SeptentrioPolaRx4/4TR，能够输出的GPS码观测类型包括C1C、C1W、C2W、C2L及C5Q5类。以GPS静态精密单点定位(precisepointpositioning,PPP)的单天解作为坐标参考“真值”，基于动态SPP估计测站坐标及接收机钟差参数。SPP数据处理中，观测数据采样率为60s，卫星截止高度角为100，卫星轨道及钟差采用广播星历的轨道及钟差参数，对流层误差采用UNB3m模型改正[24]，单频SPP中电离层误差采用GPS广播星历发播的Klobuchar模型改正。

图5　MGEX试验网测试站分布Fig.5　Distribution of the selected MGEX stations

表 3给出了5种不同的SPP定位试验方案。设计这5种试验方案目的有3点：①通过分析C2L观测量采用与不采用ISC参数改正后的位置解精度，分析ISC参数对GPS单频SPP定位的影响。②通过分析C1C+C2L(即L1C/A+L2C)消电离层组合采用与不采用ISC参数改正后的位置解精度，分析ISC参数对GPS双频SPP定位的影响。③通过对比C1C+C2L与C1W+C2W[即L1P(Y)+L2P(Y)]消电离层组合SPP精度，分析GPS普通用户与授权用户定位精度的差异。需要说明的是，利用C1W和C2W进行定位时仅考虑了试验期间能够同时播发L2C民用信号的13颗GPS卫星。

4.2结果分析

以欧洲地区的VILL站为例，图 6给出了该站2014年DOY300—310dC2L单频SPP的定位误差分布，从左至右3幅子图分别对应N、E、U3个方向的误差分布。可以看出，采用ISC参数改正后，单频SPP的定位误差明显减小。未采用ISC参数改正时，N、E、U3个方向误差的均值分别为-0.11m、-1.90m及-1.08m，标准差分别为4.54m、4.56m及6.34m；采用ISC参数改正后，N、E、U3个方向误差的均值分别为-1.07m、0.15m及-0.65m，标准差分别为2.07m、1.54m及4.35m。采用ISC参数改正后，N、E、U3个方向的定位精度分别提高了2.34m、3.69m及2.05m。

表3　不同的定位试验方案

图6　VILL站C2L单频SPP N、E、U方向定位误差分布(2014年DOY 300—310)Fig.6　Normalized histograms of the north, east and up positioning errors of C2L SPP on VILL site (2014 DOY 300—310)

图7给出了该站2014年DOY300—310dC1C+C2L双频SPP的定位误差分布。从图中可以看出，VILL站东方向定位误差最小(-4.0～4.0m)，高程方向定位误差最大(-12.0～12.0m)。具体而言，未采用ISC参数改正时，N、E、U3个方向误差的均值分别为-0.23m、0.59m及-0.06m，标准差分别为2.97m、1.34m及3.89m；采用ISC参数改正后，N、E、U3个方向误差的均值分别为-0.04m、0.29m及-0.47m，标准差分别为1.69m、1.25m及3.06m。采用ISC参数改正后，VILL站N、E、U3个方向的定位精度分别提高了0.34m、0.17m及0.66m。

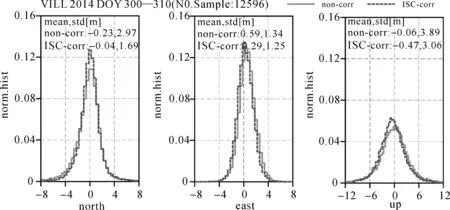
图7　VILL站C1C+C2L双频SPP N、E、U方向定位误差分布(2014年DOY 300—310)Fig.7　Normalized histograms of the north, east and up positioning errors of C1C+C2L SPP on VILL site (2014 DOY 300—310)

表 4给出了试验期间不同试验方案所有测试站的定位误差RMS统计情况。可以看出，利用C2L进行单频SPP未改正ISC参数时，N、E、U3个方向的误差分别为5.174m、4.012m及7.093m；采用ISC参数改正后，N、E、U3个方向的定位精度提高了40.1%、46.0%及23.8%，分别达到3.653、2.146及5.284m。C2L单频SPP三维定位精度提高了30.0%，由改正前的9.765m提高到6.889m。利用C1L+C2L进行双频SPP未改正ISC参数时，N、E、U3个方向的误差分别为1.588m、1.295m及3.172m；采用ISC参数改正后，N、E、U3个方向的定位精度提高了9.5%、10.2%及13.0%，分别达到1.432m、1.165m及2.748m。C1L+C2L双频SPP三维定位精度提高了12.2%，由改正前的3.786m提高到3.317m。单频SPP中除ISC外的其他误差改正项均相同，ISC参数本身的误差影响较小，改正ISC参数能够显著提高单频SPP的定位精度；双频消电离层组合在消除电离层误差的同时也放大了测码伪距观测噪声的影响，双频SPP中ISC参数本身的误差也会被进一步放大，这可能是改正ISC后双频SPP不如单频SPP精度提升的原因之一。此外，C1C与C2L组合定位采用ISC改正后的三维定位精度略高于C1W与C2W消电离层组合的定位精度(3.317mvs. 3.441m)。这表明，采用ISC参数改正后，L1C/A+L2C民用信号的双频定位精度与当前L1P(Y)+L2P(Y)消电离层组合定位精度相当。

表4不同试验方案定位误差RMS统计

Tab.4Rootmeansquare(RMS)ofdifferentstandardpositioningschemes

观测量ISC改正RMSN/mE/mU/m3D/mC2Lnon_corr5.1744.0127.0939.765C2LISC_corr3.6532.1495.2846.889精度提升/(%)-40.146.023.830.6C1C+C2Lnon_corr1.5881.2953.1723.786C1C+C2LISC_corr1.4321.1652.7483.317精度提升/(%)-9.510.213.012.2C1W+C2W-1.5051.2032.8303.441

注：Imp.=|RMSISC_corr-RMSnon_corr|/RMSnon_corr

5　结　论

针对GPS民用导航星历中新增的ISCC/A、ISCL2C、ISCL5I和ISCL5Q4种ISC参数，本文给出了GPSISC参数的含义及其在GPS标准单点定位中的使用方法，利用不同机构(包括IGG、DLR及CODE)提供的后处理DCB产品评估了GPS广播的TGD及ISC参数的实际精度，深入分析了ISC参数对GPS导航用户单/双频定位精度的影响。结果表明：

(1)GPS广播的卫星钟差参数由L1P(Y)和L2P(Y)消电离层组合计算得到，单独或联合采用民用信号实施SPP时，需同时引入TGD及ISC参数作为改正信息。

(2)ISC参数更新频次较有规律，2014年4月至2015年4月期间，各卫星ISC参数在2014年6月及2015年2月分别更新了一次。

(3)TGD及ISC参数与不同机构后处理DCB产品的比较结果略有差异，总体而言，ISCC/A参数精度可以达到0.2ns，TGD、ISCL2C及ISCL5Q参数精度能够达到0.5ns。

(4) 同一类型GPS卫星TGD与ISC参数之间的差异较小，不同类型卫星TGD与ISC参数之间的差异较大，TGD及ISC参数对GPS定位影响不能忽略。

(5) 经由TGD及ISC参数改正后，GPS民用导航信号L2C单频SPP精度提升显著，L1C/A+L2C双频SPP精度与L1P(Y)+L2P(Y)消电离层组合的定位精度相当。

致谢：感谢OliverMontenbruck博士在本文研究中提供的帮助。

[1]袁运斌, 欧吉坤.GPS观测数据中的仪器偏差对确定电离层延迟的影响及处理方法 [J]. 测绘学报, 1999, 28(2): 19-23.

YUANYunbin,OUJikun.TheEffectsofInstrumentalBiasinGPSObservationsonDeterminingIonosphericDelaysandtheMethodsofItsCalibration[J].ActaGeodaeticaetCartographicaSinica, 1999, 28(2): 19-23.

[2]LIZishen,YUANYunbin,FANLei,etal.DeterminationoftheDifferentialCodeBiasforCurrentBDSSatellites[J].IEEETransactionsonGeoscienceandRemoteSensing, 2014, 52(7): 3968-3979.

[3]MONTENBRUCKO,HAUSCHILDA,STEIGENBERGERP.DifferentialCodeBiasEstimationUsingMulti-GNSSObservationsandGlobalIonosphereMaps[J].Navigation, 2014, 61(3): 191-201.

[4]常青, 张东和, 萧佐, 等.GPS系统硬件延迟估计方法及其在TEC计算中的应用 [J]. 地球物理学报, 2001, 44(5): 596-601.

CHANGQing,ZHANGDonghe,XIAOZuo,etal.AMethodforEstimatingGPSInstrumentalBiasesandItsApplicationinTECCalculation[J].ChineseJournalofGeophysics, 2001, 44(5): 596-601.

[5]张小红, 李征航, 蔡昌盛. 用双频GPS观测值建立小区域电离层延迟模型研究[J]. 武汉大学学报(信息科学版), 2001, 26(2): 140-143, 159.

ZHANGXiaohong,LIZhenghang,CAIChangsheng.StudyonRegionalIonosphericModelUsingDual-frequencyGPSMeasurements[J].GeomaticsandInformationScienceofWuhanUniversity, 2001, 26(2): 140-143, 159.

[6]章红平, 施闯, 唐卫明. 地基GPS区域电离层多项式模型与硬件延迟统一解算分析 [J]. 武汉大学学报(信息科学版), 2008, 33(8): 805-809.

ZHANGHongping,SHIChuang,TANGWeiming.UnitedSolutiontoPolynomialVTECModelingandDCBAnalysisUsingGround-basedGPSObservations[J].GeomaticsandInformationScienceofWuhanUniversity, 2008, 33(8): 805-809.

[7]张宝成, 欧吉坤, 袁运斌, 等. 利用非组合精密单点定位技术确定斜向电离层总电子含量和站星差分码偏差 [J]. 测绘学报, 2011, 40(4): 447-453.ZHANGBaocheng,OUJikun,YUANYunbinetal.CalibrationofSlantTotalElectronContentandSatellite-receiver’sDifferentialCodeBiaseswithUncombinedPrecisePointPositioningTechnique[J].ActaGeodaeticaetCartographicaSinica, 2011, 40(4): 447-453.

[8]ZHANGBaocheng,TEUNISSENPJG.CharacterizationofMulti-GNSSBetween-ReceiverDifferentialCodeBiasesUsingZeroandShortBaselines[J].ScienceBulletin, 2015, 60(21): 1840-1849.

[9]MONTENBRUCKO,HAUSCHILDA.CodeBiasesinMulti-GNSSPointPositioning[C]∥ProceedingsofIONITM2013.SanDiego:InstituteofNavigation, 2013: 616-628.

[10]DACHR,BROCKMANNE,SCHAERS,etal.GNSSProcessingatCODE:StatusReport[J].JournalofGeodesy, 2009, 83(3-4): 353-365.

[11]MONTENBRUCKO,STEIGENBERGERP,KHACHIKYANR,etal.IGS-MGEX:PreparingtheGroundforMulti-constellationGNSSScience[C]∥Proceedingsofthe4thInternationalColloquiumonScientificandFundamentalAspectsoftheGalileoSystem.Galile: [s.n.], 2013, 9(1): 42-49.

[12]SCHAERS.DifferentialCodeBiases(DCB)inGNSSAnalysis[C]∥ProceedingsofIGSWorkshop2008.MiamiBeach:SwissFederalOfficeofTopographySwisstopo, 2008.

[13]吴晓莉, 平劲松, 刘利, 等. 区域卫星导航系统硬件延迟解算 [J]. 武汉大学学报(信息科学版), 2011, 36(10): 1218-1221.

WUXiaoli,PINGJinsong,LIULi,etal.HardwareDelaySolutionofRegionalSatelliteNavigationSystem[J].GeomaticsandInformationScienceofWuhanUniversity, 2011, 36(10): 1218-1221.

[14]GUOFei,ZHANGXiaohong,WANGJinling.TimingGroupDelayandDifferentialCodeBiasCorrectionsforBeiDouPositioning[J].JournalofGeodesy, 2015, 89(5): 427-445.

[15]MICHAELRivers.The2SOPSUserRangeAccuracy(URA)ImprovementandBroadcastInter-frequencyBias(TGD)Updates[C]∥Proceedingsofthe13thInternationalTechnicalMeetingoftheSatelliteDivisionoftheInstituteofNavigation(IONGPS2000).SaltLakeCity,UT:ION, 2000: 2551-2555.

[16]MONTENBRUCKO,LANGLEYRB,STEIGENBERGERP.FirstLiveBroadcastofGPSCNAVMessages[J].GPSWorld, 2013, 24(8): 14.

[17]FEESSW,COXJ,HOWARDE,etal.GPSInter-signalCorrections(ISCs)Study[C]∥Proceedingsofthe26thInternationalTechnicalMeetingoftheSatelliteDivisionoftheInstituteofNavigation(IONGNSS2013).Nashville,TN: [s.n.], 2013: 951-958.

[18]STEIGENBERGERP,MONTENBRUCKO,HESSELSU.PerformanceEvaluationoftheEarlyCNAVNavigationMessage[C]∥Proceedingsofthe2015InternationalTechnicalMeetingoftheInstituteofNavigation.DanaPoint,California:LagunaCliffsMarriott, 2015: 155-163.

[19]IS-GPS-200NavstarGPSSpaceSegment/NavigationUserInterfaces[S].Calif,USA:RevisionG,GPSDirectorate, 2004.

[20]LIZishen,YUANYunbin,LIHuietal.Two-stepMethodfortheDeterminationoftheDifferentialCodeBiasesofCompassSatellites[J].JournalofGeodesy, 2012, 86(11): 1059-1076.

[21]WANGNingbo,YUANYunbin,LIZishen,etal.DeterminationofDifferentialCodeBiaseswithMulti-GNSSObservations[J].JournalofGeodesy, 2016, 90(3): 209-228.

[22]张宝成, 欧吉坤, 袁运斌, 等. 基于GPS双频原始观测值的精密单点定位算法及应用 [J]. 测绘学报, 2010, 39(5): 478-483.

ZHANGBaocheng,OUJikun,YUANYunbin,etal.PrecisePointPositioningAlgorithmBasedonOriginalDual-frequencyGPSCodeandCarrier-phaseObservationsandItsApplication[J].ActaGeodaeticaetCartographicaSinica, 2010, 39(5): 478-483.

[23]WILSONBD,YINGERCH,FEESSWA,etal.NewandImproved:theBroadcastInterFrequencyBiases[J].GPSWorld, 1999, 10(9): 56-66.

[24]LEANDROR,SANTOSM,LANGLEYR.UNBNeutralAtmosphereModels:DevelopmentandPerformance[C]∥ProceedingsofIONNTM2006.Monterey,CA:HyattRegencyHotel, 2006: 18-20.

(责任编辑：陈品馨)

修回日期： 2016-06-07

E-mail：wnbigg@asch.whigg.ac.cn

AccuracyEvaluationofGPSBroadcastInter-signalCorrection(ISC)ParametersandTheirImpactsonGPSStandardPositioning

WANGNingbo1,3,YUANYunbin1,ZHANGBaocheng1,LIZishen2

1.StateKeyLaboratoryofGeodesyandEarth’sDynamics,InstituteofGeodesyandGeophysics,ChineseAcademyofSciences,Wuhan430077,China; 2.AcademyofOpto-Electronics,ChineseAcademyofSciences,Beijing100094,China; 3.UniversityofChineseAcademyofSciences,Beijing100049,China

WiththeintroducingofGPS(GlobalPositioningSystem)BlockIIR-Msatellitesin2005,anewcivilsignal(L2C)wastransmittedonL2frequency,andtwonewsignals(L5IandL5Q)onanewfrequency(L5)werealsointroducedasstandardsignalswithBlockIIFsatellitesbeginningin2010.Inadditiontothetiminggroupdelay(TGD)parametercontainedinthelegacynavigation(LNAV)message,fouradditionalinter-signalcorrection(ISC)parametersareintroducedinthenewcivilnavigation(CNAV)messagetoprovidecorrectionsforL1C/A,L2CandL5signalswithrespecttoL1P(Y)signal.Inthisstudy,theISCcorrectionmodelsarefirstdevelopedforGPSsingle-anddual-frequencynavigationusers.ThereafterISCsarevalidatedwiththedifferentialcodebias(DCB)productsofdifferentorganizations,andseveralstandardpointpositioning(SPP)schemesarealsocarriedouttoanalyzetheimpactofISCsonGPSstandardpositioning.TheresultsindicatethattheprecisionofbroadcastISCC/Aisabout0.2ns,andthoseofTGD,ISCL2CandISCL5Qareabout0.5ns.ThepositioningaccuracyoftheSPPsolutionbasedonGPSL2CsignalsapplyingISCcorrectionsimproves30.6%andthatbasedonL1C/AandL2Cionosphere-freecombinationimproves12.2%at12multi-GNSSexperiment(MGEX)stationsduringdayofyear(DOY) 300—310in2014,comparedtothesolutionswithouttheconsiderationofISCs.ForGPSdual-frequencyusers,thebroadcastISCsenablealevelofaccuracythatiscompetitivewithionosphere-freecombinationofthepresentL1P(Y)andL2P(Y)signals.

inter-signalcorrection(ISC);timinggroupdelay(TGD);differentialcodebias(DCB);standardpositioning

WANGNingbo(1987—)，male，PhDcandidate，majorsinmulti-GNSSdifferentialcodebias(DCB)processingandionosphericTECmodeling.

P228

A

1001-1595(2016)08-0919-10

国家自然科学基金(41231064；41304034；41574033；41321063)；北京市自然科学基金(4144094)

2015-11-17

王宁波(1987—)，男，博士生，研究方向为多模GNSS差分码偏差处理及电离层TEC建模。

引文格式：王宁波，袁运斌，张宝成，等.GPS民用广播星历中ISC参数精度分析及其对导航定位的影响[J].测绘学报，2016,45(8)：919-928.DOI:10.11947/j.AGCS.2016.20150554.

WANGNingbo,YUANYunbin,ZHANGBaocheng,etal.AccuracyEvaluationofGPSBroadcastInter-signalCorrection(ISC)ParametersandTheirImpactsonGPSStandardPositioning[J].ActaGeodaeticaetCartographicaSinica,2016,45(8):919-928.DOI:10.11947/j.AGCS.2016.20150554.