对于带未知噪声的多传感器系统信息融合辨识算法*

李恒,韩波，2, 王戴木, 赵正平,李怀敏

(1.阜阳师范学院 计算机与信息工程学院，安徽 阜阳 236037；2.东南大学 毫米波国家重点实验室，南京 210096)



对于带未知噪声的多传感器系统信息融合辨识算法*

李恒1,韩波1，2, 王戴木1, 赵正平1,李怀敏1

(1.阜阳师范学院 计算机与信息工程学院，安徽 阜阳 236037；2.东南大学 毫米波国家重点实验室，南京 210096)

对于一个带未知噪声的多传感器系统，当各种噪声方差和噪声之间的协方差都不为0时，提出了一种基于自回归滑动平均(ARMA)模型的多段辨识算法.使用该算法可以得到对系统未知参数和未知噪声方差和协方差的无偏估计，并且证明了估计的收敛性.并通过一个Matlab仿真例子对算法的有效性做出了证明.

多传感器系统；未知噪声；自回归滑动平均模型；噪声方差；噪声协方差

多传感器信息融合在通信、目标跟踪、目标识别等领域中得到广泛应用[1].利用Kalman滤波等工具在被噪声污染了的观测信息中提取有用信号被称为最优滤波理论[2].在最优滤波理论中，通常要求已知系统的精确参数和精确的噪声统计信息[3].而在实际应用中，系统参数和噪声统计往往是部分未知或者完全未知的[4].对于带未知噪声的系统，如果利用Kalman滤波理论构造自校正估值器，需要在线辨识系统噪声统计和未知参数[5].自回归滑动平均模型(ARMA模型)是自动控制领域的重要模型，在实际控制领域有着广泛应用，很多实际问题通常可以用ARMA模型表示[6].文献[7～9]提出了对于带噪声的ARMA模型的多段辨识算法，这些算法都比较相似，在文献[7]中概况为：第一段，用最小二乘法及推广方法得到对AR(自回归)参数的局部和全局融合估值；第二段，用相关函数法得到对噪声统计的局部和全局融合估值；第三段，用系统辨识算法得到对MA(滑动平均)参数的估值.在文献[9]中，对于带未知参数和噪声的多传感器系统，假设部分噪声和参数是未知的，并且假设输入噪声w(t)和观测噪声vi(t)不是独立的噪声，而是具有协方差不为0的相关噪声，针对这一情形，文献[9]进行了两段在线辨识.本文在文献[9]的基础上，提出一种普遍情形，即系统内的各种噪声都不是独立噪声时，也就是系统的各种噪声的方差和协方差都不为0时，通过多段辨识方法，辨识出系统的未知参数和系统的各种未知噪声的方差和协方差.

1　问题的提出

考虑一个多传感器目标跟踪系统，可对其构造出ARMA模型如下

A(q-1)s(t)=C(q-1)w(t)

(1)

yi(t)=s(t)+vi(t)+ξ(t),i=1,...,L(2)

(2)

在式(1)和(2)组成的模型中，t表示离散时刻或者递推运算中的“步”(可以是秒或者毫秒或者其他的时间单位)，L为传感器的个数，并且假设s(t)、yi(t)、vi(t)、w(t)和ξ(t)分别表示系统的目标状态、第i个传感器的观测值、第i个传感器的观测噪声、系统输入噪声和公共干扰噪声.A(q-1)和C(q-1)是多项式矩阵，均有形式

X(q-1)=X0+X1q-1+…+Xnxq-nx

(3)

式中，q-1为滞后算子，q-1x(t+1)=x(t).假设以下条件成立：1)A(q-1)的结构已知而参数未知，C(q-1)的结构和参数都是已知的.2)vi(t)、w(t)和ξ(t)是零均值的噪声，噪声方差和协方差用Qxy表示(x和y为w(t)、vi(t)和ξ(t)三者中的二者)，特别当x=y时，Qxx为x(t)的方差.这些噪声方差和协方差是未知的.3)观测yi(t)(i=1,...,L)对于t以概率1有界.问题是对式(1)和(2)组成的多传感器ARMA模型，在以上的3个假设为前提条件下，基于已知观测yi(t)(i=1,...,L) 如何估计未知参数A(q-1)和噪声统计方差Qxx和协方差Qxy(x≠y)的值.

2　辨识算法

第1段 辨识AR参数A(q-1)

由式(1)，(2)有

(4)

A(q-1)yi(t)=C(q-1)w(t)+A(q-1)ξ(t)+A(q-1)vi(t)

(5)

可定义

zi(t)=C(q-1)w(t)+A(q-1)ξ(t)+A(q-1)vi(t)

(6)

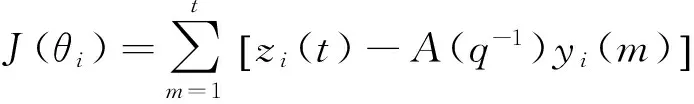
第2段 辨识未知噪声方差和噪声协方差

由式(6)可得zi(t)的采样相关函数的估值[8]为

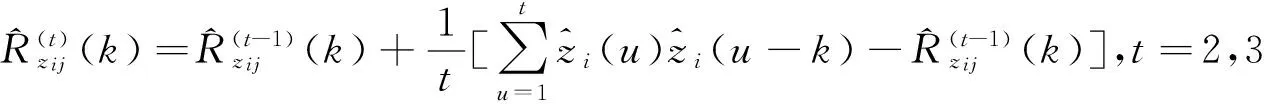
(7)

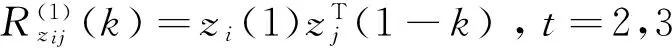
则由式(6)可求zi(t)的相关函数

(8)

其中n0=max(na,nc)，k=0,1,…,n0，且显然有Rzij(k)=0,k>n0.当i=j时，式(8)可变为

(9)

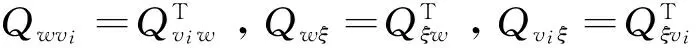
Ωiθi=δi

(10)

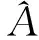
Pi(q-1)=1+pi1q-1+…+pinpiq-npi，R(q-1)=1+r1q-1+…rnrq-nr，

则式(6)可变为

zi(t)=C(q-1)w(t)+A(q-1)Pi(q-1)η(t)+A(q-1)R(q-1)λ(t)

(11)

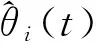
定理对于一个带噪声的用式(1)和(2)表示的多传感器模型，在假设条件1)～3)下，按照两段算法辨识，所得的参数估计，以及噪声方差和协方差，估值均以概率1收敛于真实值.

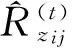
3　特定情形及对相关例子的Matlab仿真

对于以上提出的算法，可针对一特定情形，此情形假设vi(t)和ξ(t)不相关，w(t)和ξ(t)不相关，则Qviξ和Qwξ为0，则式(8)可变为

(12)

式(9)可变为

(13)

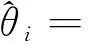
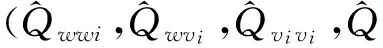
(14)

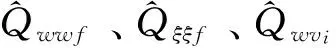
例 设有一个3传感器的跟踪系统有ARMA模型如式(1)，(2)所示，其中设na=2，nc=2，a1=1，a2=0.5， c1=0.2，另设各噪声方差与协方差为Qww=0.3，Qξξ=0.1，Qv1v1=0.1，Qwv1=0，Qwv2=0.06，Qwv3=0.08，Qv1v1=0.02，Qv2v2=0.03，Qv3v3=0.05，Qv1v2=0.005，Qv1v3=0.055，Qv2v3=0.08，其中A(q-1)的参数a1和a2未知的，系统的各噪声方差和协方差均未知.

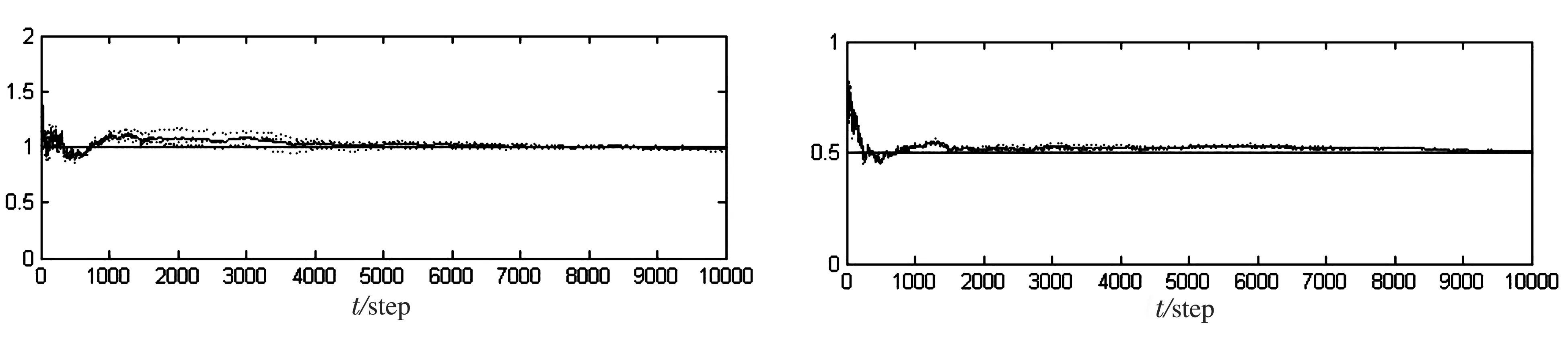
a　a1和　　　　　　　　　　　　　b　 a2和

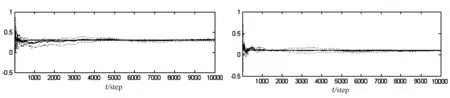
a　Qww 和和

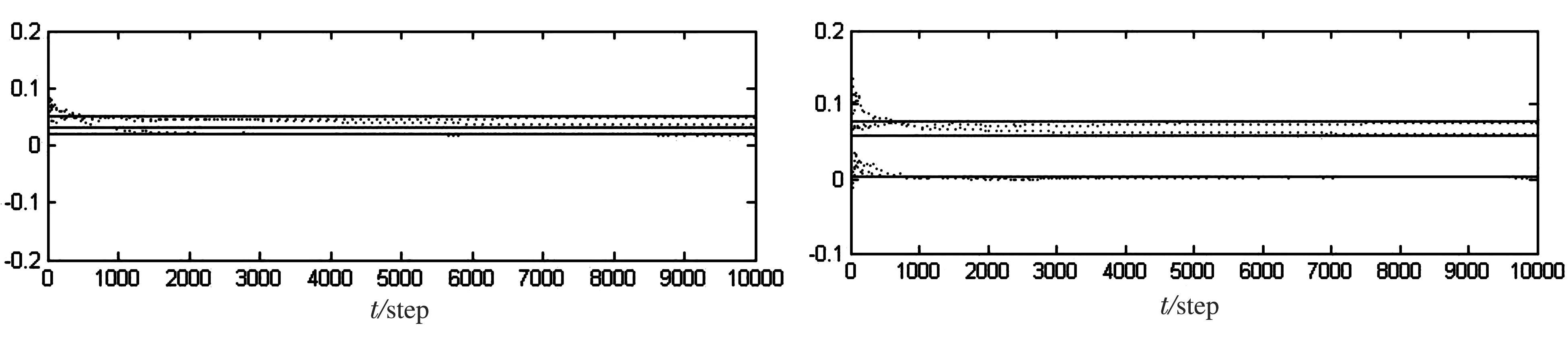
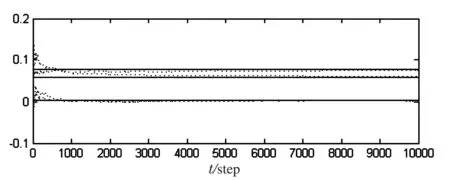
e　Qwvi(i,j=1,2,3)和

从图1，图2看出，辨识结果在步数大于2 000时，均能稳定的收敛于真实值，特别是到5 000步之后的每一步的估值都可以作为对真实值的估值用于滤波场合，为保险起见，统一设步数为10 000，得到的估值收敛特性良好，满足实用的精度要求.

4　结语

本文在文献[9]的基础上，提出一种普遍情形，即系统内的各种噪声都不是独立噪声，各种噪声的方差和协方差都不为0时，通过多段辨识方法，辨识出系统的未知参数和系统的各种噪声的未知方差和协方差.从仿真例子可以看出，估值的收敛性良好，在一定的误差允许范围内，可以代替真实值应用于滤波场合.本文讨论的是一种特殊情形，针对普遍情形符合的其他情形，还有很多讨论空间.

[1]P. J. Dua, S. C. Liu, J. S. Xia and Y. D. Zhao. Information fusion techniques for change detection from multi-temporal remote sensing images[J]. Information Fusion, 2013,14(1): 19-27.

[2]邓自立.信息融合滤波理论及其应用[M].哈尔滨:哈尔滨工业大学出版社,2007.

[3]Gao Y,Xa H Q,Deng Z L.Multi-stage information fusion identification method for multisensor ARMA signals with white measurement noises[J].2010 8th IEEE International Conference on Control andAutomation,2010,10(2):1115.

[4]丁锋.系统辨识(4):辅助模型辨识思想与方法[J].南京信息工程大学学报:自然科版,2011,3(4):289-318

[5]周曜. 非线性估计中无味滤波(UKF)与扩展卡尔曼滤波(EKF)之比较研究[J].宜春学院学报,2009,31(2):52-54.

[6]Liu J F,Deng Z L.An information fusion identification method for multisensor autoregressive moving average signals with white measurement noise and sensor bias[J].Sensors Letters,2011,9:1443-1447.

[7]贾文静，张鹏，邓自立.辨识动态系统噪声方差Q和R的新方法[J].科学技术与工程,2006,6(14):2008-2011.

[8]李恒.对于带有色噪声的多传感器系统两段辨识信息融合算法[J].宜春学院学报,2015,37(6):13-16.

[9]高媛.多传感器系统模型参数和噪声统计的一种信息融合辨识方法[J].科学技术与工程,2009,9(17)：4896.

[10]李怀敏.广义系统降阶分布式信息融合稳态Kalman滤波器[J].阜阳师范学院学报:自然科学版,2015,32(9):70-75.

Information Fusion Identification Algorithm for the Multi-sensor System with Unknown Noises

LI Heng1, HAN Bo1,2, WANG Dai-mu1, ZHAO Zheng-ping1, LI Huai-min1

(1.School of Computer and Information Engineering, Fuyang Teachers’ College, Fuyang Anhui 236037，China； 2.State Key Laboratory of Millimeter Waves，Southeast University，Nanjing Jiangsu 210096，China)

For the multi-sensor system with unknown noises，when all kinds of the noise variance and covariance are not 0, based on the Autoregressive Moving Average(ARMA) innovation models, a multi-stage identification algorithm is presented. Using this algorithm can get unbiased estimations of the unknown parameters and the unknown noise variance and covariance and the convergence of the estimations is proved. A Matlab simulation example shows the effectiveness of the algorithm.

multi-sensor system; ARMA model; unknown noise; noise variance; noise covariance

1673-2103(2016)02-0057-05

2015-12-15

国家自然科学基金(No.61401101);东南大学毫米波国家重点实验室开放课题(No.K201401);安徽省教育厅自然科学项目(No.2015KJ012,2015KJ007);阜阳师范学院科技成果孵化基金项目(No.2013KJFH05);阜阳师范学院自然科学项目(No.2015FSKJ10,No.2015FSKJ11)

李恒(1985-)，男，安徽宿州人，讲师，硕士，研究方向：系统辨识状态估计;王戴木(1957-)，男，安徽安庆人，教授，博士，研究方向：计算机控制.

TP273

A