一类具有非线性发生率的时滞传染病模型Hopf分支*

张子振，缑超博，张振辉

(安徽财经大学管理科学与工程学院,安徽 蚌埠 233030)



一类具有非线性发生率的时滞传染病模型Hopf分支*

张子振，缑超博，张振辉

(安徽财经大学管理科学与工程学院,安徽 蚌埠 233030)

以恢复个体临时免疫期时滞为分支参数，研究了一类具有阶段结构和非线性发生率的时滞SIRS传染病模型的局部Hopf分支.首先计算得到模型的有病毒平衡点，然后通过分析模型相应特征方程根的分布， 得到模型有病毒平衡点局部渐近稳定和产生Hopf分支的时滞临界点τ0.研究表明，当时滞的值低于临界点τ0时，有病毒平衡点是局部渐近稳定的.而一旦时滞的值超越临界点，模型的有病毒平衡点将失去稳定性并在有病毒平衡点附近产生一簇分支周期解.最后，利用仿真示例对理论分析结果的正确性进行了验证.

SIRS模型；阶段结构；时滞；Hopf分支

引言

数学模型已经成为分析传染病传播、控制机理的一种重要的工具.近年来，不少研究学者利用微分方程描述传染病传播模型[1～5].以上文献都是针对具有双线性发生率的传染病传播模型展开的研究工作.基于双线性发生率建立的传染病传播模型，假设疾病感染人数是线性增长的.然而，一位感染者在单位时间内所接触的群体规模是有限的.因此，具有非线性发生率的传染病传播模型受到研究学者的广泛关注[6～8].文献[8]提出了下列具有非线性发生率和阶段结构的时滞传染病模型：

(1)

其中，X(t)表示幼年阶段人口在t时刻的密度， S(t)，I(t)和R(t)分别表示成年阶段人口中易感者、感染者和恢复者在t时刻的密度.A，B，α，β，γ，δ，σ，ε和μ为为模型(1)的参数，具体含义可以参考文献[8]. τ为疾病的潜伏期时滞.文献[8]以时滞τ为分支参数研究了模型(1)的Hopf分支存在性以及分支的性质.但是现实世界中，每个恢复状态的个体，经过一段时间的临时免疫期之后才能再次成为易感者.基于此，本文考虑如下时滞传染病模型：

(2)

其中，τ为恢复个体临时免疫期时滞.本文主要研究时滞τ对模型(2)局部稳定性的影响.

1　有病毒平衡点局部稳定性分析

经过计算可知，当Aβσ+βσ(μ+ε+γ)>μ(μ0+σ)(μ+ε+γ)，并且(μ+δ)(μ0+σ)(μ+ε+γ)(μα+β)>Bασ(μ+δ)(μ+ε+γ)+βγδ(μ0+σ)时，系统(2)存在唯一有病毒平衡点E*(X*,S*,I*,R*)，

其中，

作平移变换u1(t)=X(t)-X*, u2(t)=S(t)-S*, u3(t)=I(t)-I*,u4(t)=R(t)-R*.仍然记u1(t),u2(t),u3(t),u4(t)为 X(t),S(t),I(t)和R(t).

系统(2)在有病毒平衡点E*(X*,S*,I*,R*)处的线性化部分为:

(3)

其中,

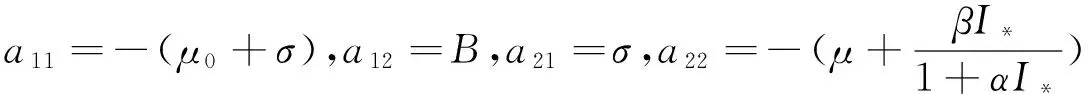
a44=-μ, b44=-δ.

于是，系统(3)的特征方程为：

λ4+p3λ3+p2λ2+p1λ+p0+(q3λ3+q2λ2+q1λ+q0)e-λτ=0

(4)

其中，

p0=a33a44(a11a22-a12a21)-a11a23a32a44,

p1=(a12a21-a11a22)(a33+a44)+a23a32(a1+a10)-a9a10(a11+a44)-a33a44(a11+a22),

p2=a11a22+a33a44-a12a21-a23a32+(a11+a22)(a33+a44),

p3=-(a11+a22+a33+a44),

q0=a11a32a43b24-a11a23a32b44-a12a21a33b44,

q1=(a12a21+a23a32-a11a22-a11a33-a22a33)b44-a32a43b24,

q2=a11a22+a33a44-a12a21-a23a32+(a11+a22)(a33+a44),q3=-b44.

当τ=0时，方程(4)变为

λ4+p03λ3+p02λ2+p01λ+p00=0.

(5)

其中，p00=p0+q0,p01=p1+q1,p02=p2+q2, p03=p3+q3

根据赫尔维茨稳定性判据可知，如果条件(H1)即：方程(6)～(9) 成立, 则模型(2)的有病毒平衡点E*(X*,S*,I*,R*)是局部渐近稳定的.

Det1=A03>0

(6)

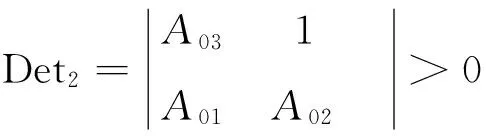
(7)

(8)

(9)

当τ>0时，令λ=iω*(ω*>0)为特征方程(4)的根，有

(10)

从而，有

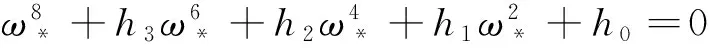
(11)

其中，

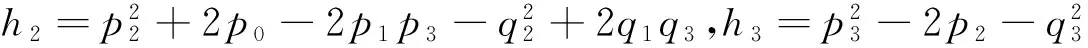
下面，假设：(H2):方程(11)至少存在有一个正根.如果条件(H2)成立，那么方程(11)存在一个正根 ω*0使得方程(4)存在一对纯虚根±iω*0.进而得到

对方程(4) 的左右两端分别对τ进行求导, 得到

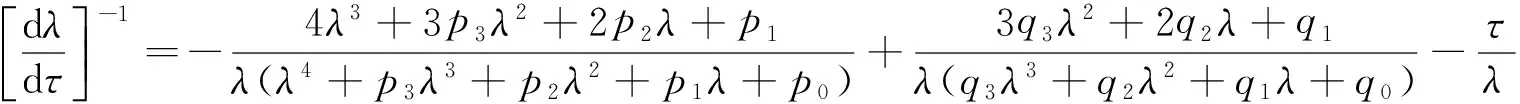
因此，

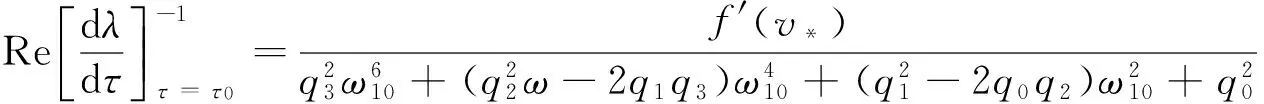
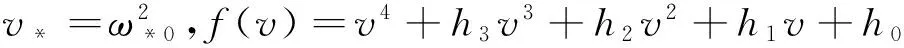
定理1对于模型(2)，如果(H1)～(H3)成立，则当 τ∈[0,τ0)时,模型(2) 的有病毒平衡点E*(X*,S*,I*,R*)是局部渐近稳定的；模型(2)在τ=τ0附近产生Hopf分支，并在有病毒平衡点E*(X*,S*,I*,R*)处产生一簇分支周期解.

2　仿真示例

取A=15,B=1,σ=2.85，μ0=0.03，μ=0.01,α=0.012，β=0.25,δ=0.51,ε=0.2,γ=0.15.得到下列系统：

(12)

系统(12)存在唯一有病毒平衡点E*(6.205 8,2.872 7,82.910 1,23.916 4).进而得到ω0=0.884 5,τ0=4.025 7.当τ=3.35∈[0,4.025 7)时，系统(12)是局部渐近稳定的，仿真效果如图2所示.当τ=4.275>4.025 7时，系统(12)在E*(6.205 8,2.872 7,82.910 1,23.916 4)附近产生一簇分支周期解.仿真效果如图4所示.

图1: 当τ=3.35<τ0=4.025 7时，系统(12)渐近稳定

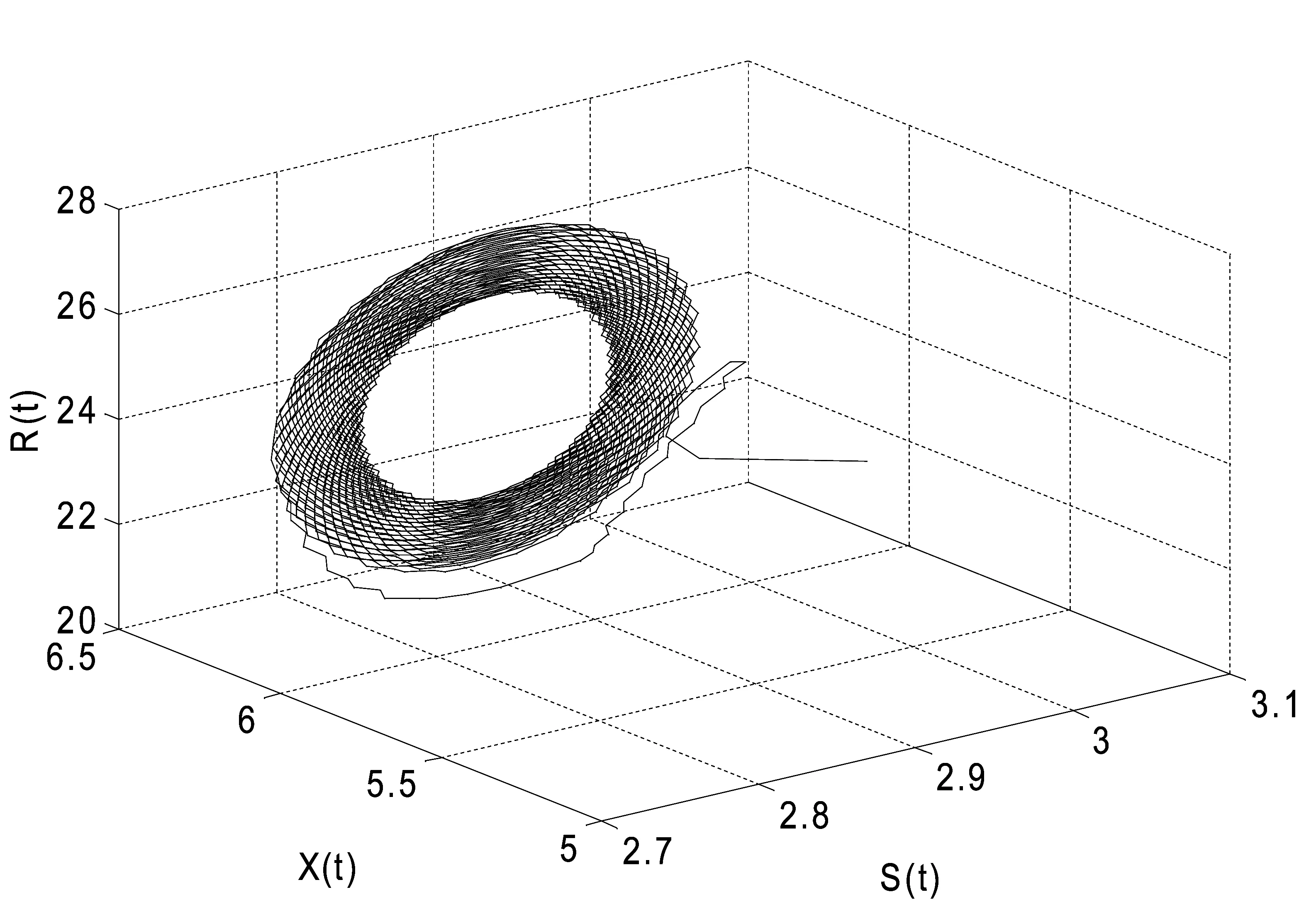
图2: 当τ=4.275>τ0=4.025 7时，系统(12)失去稳定性

图3: 当τ=3.35<τ0=4.025 7时，系统(12)渐近稳定

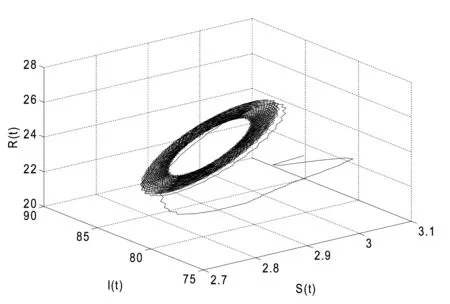
图4: 当τ=4.275>τ0=4.025 7时，系统(12)失去稳定性

3　结论

本文基于文献[9]中的具有阶段结构的时滞传染病模型，并考虑到恢复个体对疾病的临时免疫期，提出了另外一种形式的具有阶段结构和时滞SIRS传染病模型.首先给出模型有病毒平衡点存在的充分性条件，然后以时滞为分支参数，利用特征值方法分析得到有病毒平衡点局部渐近稳定和模型产生Hopf分支的时滞临界点τ0. 并给出仿真示例对理论分析结果的正确性进行了验证.研究表明，当时滞τ∈[0,τ0)时，便于采取措施对疾病的传播进行有效控制.当τ>τ0时，此时将不利于控制疾病在社会中的传播.

[1]Wang J.J, Zhang J.Z, Jin Z, Analysis of an SIR model with bilinear incidence rate [J].Nonlinear Analysis: Real World Applications, 2010, 11 (4): 2390-2402.

[2]Zhang T.L, Liu J.L, Teng Z.D. Stability of Hopf bifurcation of a delayed SIRS epidemic model with stage structure [J]. Nonlinear Analysis: Real World Applications, 2010, 11(1): 293-306.

[3]Wan H, Cui J. A. Rich dynamics of an epidemic model with saturation recovery [J]. Journal of Applied Mathematics, 2013(9),2013.

[4]Wang L. W, Yang X. F. Global stability of a delayed SIRS model with temporary immunity [J]. Chaos Solitons & Fractals, 2008, 38(1):221-226.

[5]Song M, Ma W. B. Asymptotic properties of a revised SIR epidemic model with density dependent birth rate and time delay [J]. Dynamics of Continuous, Discrete and Impulsive Systems, Series A:Mathematical Analysis, 2006, 13(2):199-208.

[6]Ruan S. G, Wang W. D. Dynamical behavior of an epidemic model with a nonliear incidence rate [J]. Journal of Differential Equations, 2003, 188(1):135-163.

[7]Yoichi E, Eleonora M, Yoshiaki M, et al. Stability analysis of delayed SIR epidemic models with a class of nonlinear incidence rates [J]. Applied Mathematics and Computation, 2012, 218(9): 5327-5336.

[8]陈方方, 洪灵. 一类具有时滞和非线性发生率的SIRS传染病模型稳定性与Hopf分岔分析[J]. 动力学与控制学报, 2014,12(1): 79-85.

[9]Hassard B. D, KazarinoffN. D, Wan Y. H. Theory and Applications of Hopf Bifurcation [M]. Cambridge University Press, Cambridge, 1981.

Hopf Bifurcation of a Delayed Epidemic Model with Nonlinear Incidence Rate

ZHANG Zi-zhen, GOU Chao-bo, ZHANG Zhen-hui

(School of Management Science and Engineering, Anhui University of Finance and Economics, Bengbu Anhui 233030, China)

Local Hopf bifurcation of a delayed epidemic model with nonlinear incidence rate and stage-structure is studied in this paper. The viral equilibrium of the model is obtained and then the critical value of the delay for local stability of the viral equilibrium and existence of local Hopf bifurcation is also obtained by analyzing distribution of roots of the corresponding characteristic equation. It is proved that the viral equilibrium is locally asymptotically stable when the value of the delay is below and it will lose its stability and generate a cluster of branching periodic solutions near a viral equilibrium point when the value of the delay is above. Finally, a numerical example is presented to testify the validity of theoretical results.

SIRS model; stage-structure; delay; Hopf bifurcation

1673-2103(2016)02-0008-05

2015-11-05

2015年度安徽省高等学校省级自然科学研究项目(KJ2015A144)

张子振(1982-)，男，山东聊城人，讲师，博士.研究方向：计算机网络安全，动力系统.

O175.12

A