地面沉降变形监测的回归分析

董咪娜，　谢小平

(曲阜师范大学 地理与旅游学院， 山东 日照 276800)



地面沉降变形监测的回归分析

董咪娜，谢小平

(曲阜师范大学 地理与旅游学院， 山东 日照 276800)

地面沉降是普遍存在的地质灾害，毁坏地面建筑设施，对环境和城市建设造成了深刻的影响。通过分析地面沉降的因素，结合地面沉降的监测方法，建立多元回归模型。通过对变形监测数据的处理和回归显著性的检验，为解决地面沉降与地下水开采的冲突提供理论支持。

变形监测；数据处理； 回归分析

地面沉降是一种全球性的地质灾害，由于深层地下水补给缓慢，被开采后，上覆地层的巨大压力造成含水层体积收缩，在宏观上即表现为地面沉降，具有时间长、分布范围广等特点。20世纪80年代以来，随着我国工农业生产和城乡居民用水量的大幅度增长，灾害面积已超过90 000 km2，涉及17个省市、90多个大中城市[1]。截止2011年12月，中国有多个城市出现了地面沉降，尤其是长三角地区、华北平原和汾渭盆地己成重灾区，沉降面积逾万平方千米，并伴生了地裂缝灾害。华北平原是我国地面沉降面积最大、类型最为复杂的地区，也是地面沉降对资源环境和经济发展影响最严重的地区之一。近年来，国内外地面沉降研究工作稳步发展，取得了大量研究成果。针对不同区域的地面沉降，开展了一系列区域地面沉降监测技术与成因机制模型研究，取得了实用性突出的研究成果，并形成了比较完善的体系。变形监测技术和方法主要向数据处理的现代算法、多时相数据的实时处理、数据挖掘和计算智能技术方面发展，形成了立体交叉的空间模式[2]。目前，地面沉降已经导致一些城市出现了路面积水、排水不畅、井管上拔等现象，严重影响了区域经济建设、社会的可持续发展和生态文明建设。全国地面沉降最为突出的是长江三角洲地区(以上海为代表)、环渤海地区(以天津为代表)和西安等地[1]。在浙江省范围内，地面沉降主要发生在地下水开采量较大、地表建筑较为集中的中心城区和部分县城城区。临安市所在的地面沉降存在发展空间大、地下流体采源深等特点，对城市建设造成了一定的影响，已成为影响区域经济社会可持续发展的重要因素之一。

本文以浙江省临安市为例，通过现场监测、数值分析等手段对地面沉降进行了研究，研究结论可为地面沉降的防治工作提供理论依据。

1　研究区域概况

浙江省临安市的某小区11号楼和12号楼建筑工程占地面积分别为710.58 m2和653.21 m2，建筑高度为97.35 m。地势平坦，主要采用地基土承载力较高的岩质地基和桩基基础的稳定框架结构，建筑周围土质为粘性土和砾土，开挖深度范围6.5～7.7 m，20期的沉降点观测中除最后5期用来检测精准度，其余各期数据都用来计算。

1.1沉降观测方案设计

1.1.1观测仪器及依据

观测仪器：徕卡电子水准仪DNA03和数码水准尺。

观测依据：《JGJ/T 8—97建筑变形测量规程》《CJJ 8—99城市测量规范》《DB21/907—2005建筑地基基础技术规范》。

1.1.2观测方法

布设基准点、工作基点和观测点。基于规范精度要求，依次找准基点布设高程控制网，高程控制网的布设要采用分级布网形式。具体步骤和操作要点如下：

(1)依据《DB21/907—2005建筑地基基础技术规范》的规定以及水文地质特点，水准点的布设应选在施工影响范围以外，即超过建筑物高度两倍的距离，且在地基稳定的现有建筑物上。如图1所示，BM1、BM2、BM3连起来可构成一条闭合水准线路。

(2)在建筑附近先布设3个基准点，顺序标号为Ⅰ、Ⅱ和Ⅲ，如图2所示。

图1　水准点分布　　　　　　　　　　　　　　图2　工作基点分布

(3)观测点布设时应选在建筑物周边、四周柱基上，可以准确反映出建筑物沉降变化位置。依据该布设原则，选择12个布设观测点A1、B1、C1、D1、E1、F1及A2、B2、C2、D2、E2、F2，如图3所示。

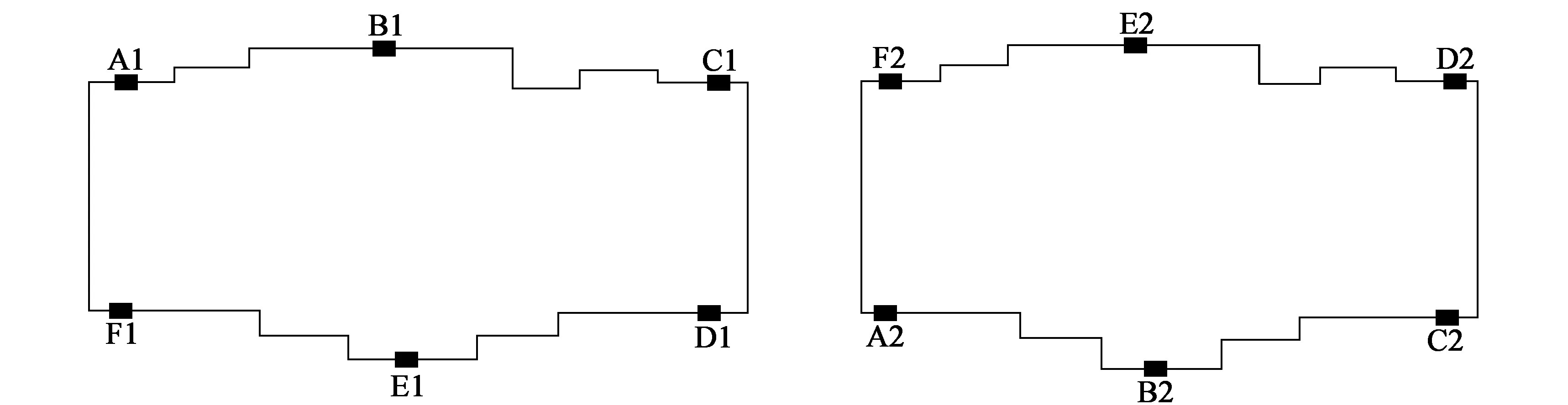
图3　观测点分布

另外，各类水准点的观测也可以采用几何水准测量方法：

(1)首先需要对闭合线路的3个基准点定期进行4次单程双观测，使用自由网平差的方法求得高程，在观测成果中选择较为稳定的起算点，再依据二级水准观测精度对水准点实施观测；

(2)利用基准点定期观测工作基点，并使用自由网平差的方法求得高程，再依据工作基点，定期对观测点实施观测，使其满足三级水准观测精度要求，平差后得出高程值。

2　回归模型的建立

2.1多元线性回归分析

回归分析法就是根据统计方法确立因变量和自变量之间的回归方程[4]。其优点一是适用于分析含有多因素的模型，二是可以得到确定性的结果，三是多用于复杂变化因素较多的情况。多元线性回归分析就是研究多个变化因素和一个确定变量间的不确定关系，找出因素间的联系。

本文依据研究区的建筑物变形程度和各个因素间的相关性，建立数学表达式：

(1)

式中：β0是常数项；t=1,2,…,n；εt是误差项随机变量，表示去除p个自变量后其他自变量对y的影响程度，服从于正态分布εt～N(0,σ2)；β0,β1,…,βp是偏回归系数，是其他变量不变时xtp每增加或减少一个单位时y的平均变化量。

其中理论方程为

(2)

2.2多元线性回归模型

多元线性回归分析是在获得影响因素的前提下，将定性问题定量化，分析确定各因素对主体问题的影响程度。其基本任务包括[5]：根据因变量与多个自变量的实际观测值，建立因变量对多个自变量的多元线性回归方程，从而检验和分析自变量对因自变量的综合线性影响的显著性。由自变量对因变量的单一性的显著性影响，只选择对因变量有显著线性影响的自变量，建立多元线性回归方程，从而评定自变量对因变量影响的相对重要性，以及测定最优多元线性回归方程的偏离度等。由于大部分多元非线性回归问题都可以化为多元线性回归问题，所以这里仅讨论多元线性回归方程。

多元线性回归模型：

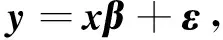
(3)

假设有n个变形量：

(4)

x元素是一般变量的观测值或自变量，有p个影响因子的形式为

(5)

回归系数为

(6)

回归系数的求解估值为

(7)

在以上公式中，y是n维变形量的观测向量；x能作用关于n×(p+1)矩阵的常规变量值；β向量能反应回归方程的系数；ε是n维随机向量，且遵循正态分布ε～N(0,σ2)。

利用数学原理的最小二乘法得出β的估算值：

(8)

以上是基于理论概述，在实际操作中，对当前状态作出假设，建立数学模型是研究问题的基本策略。从数据结构得出多元线性方程，还需进行显著性检验。

2.3多元线性回归方程的显著性检验

一般情况下，并不能明确因变量y与一些自变量x1,x2,…,xp之间是否存在相关关系时，可以先假定建立回归方程。虽然大量测量数据可以作为依据，建立相关回归方程式后，仍然需要对回归方程进行显著性检验。

第一步假设：因变量y与自变量x1,x2,…,xp间不存在线性关系。在假定模型中，β为0，可得出：

(9)

由于上述公式的限制条件，得出统计量：

(10)

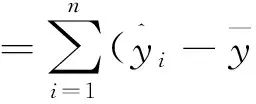
在假定公式成立时，统计量F服从F(p,n-p-1)分布规律，在选择回归拟合度α后，得出y和x1,x2,…,xp间是存在明显线性关系的，更加证实了该回归方程的显著性。

2.4多元线性回归系数的显著性检验

并非所有的自变量x1,x2,…,xp对因变量都有明显的显著作用。在排除无关变量的理想状态下，建立关系简单的线性方程，其中在变量xj和y的作用并不显著时，回归系数也为0，得到假设xj显著性为

(11)

由此可估算求得：

(12)

(13)

式中cjj为矩阵(xTx)-1主对角线上的第j个元素，若假设的结果正确，则统计量为

(14)

(15)

(16)

上述式子组建用来验证假定的统计量：

(17)

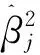
3　验证分析及评价

根据工程施工进度和基础加载情况，每完成一层就需要要观测一次。在主体工程完成后的第十天、一个月、一个季度、半年和一年期间内，如果回填土与地下水位间发生严重错位变化，或者墙体产生裂缝，两侧出现不均沉降等，要采取持续性的观测。结束观测之后，整理和计算采集的数据。以测量误差原理为依据，对每期数据进行平差计算，剔除粗误差，筛选出合格数据，不满足精度设计要求的需要重测，计算结果如表1所示。

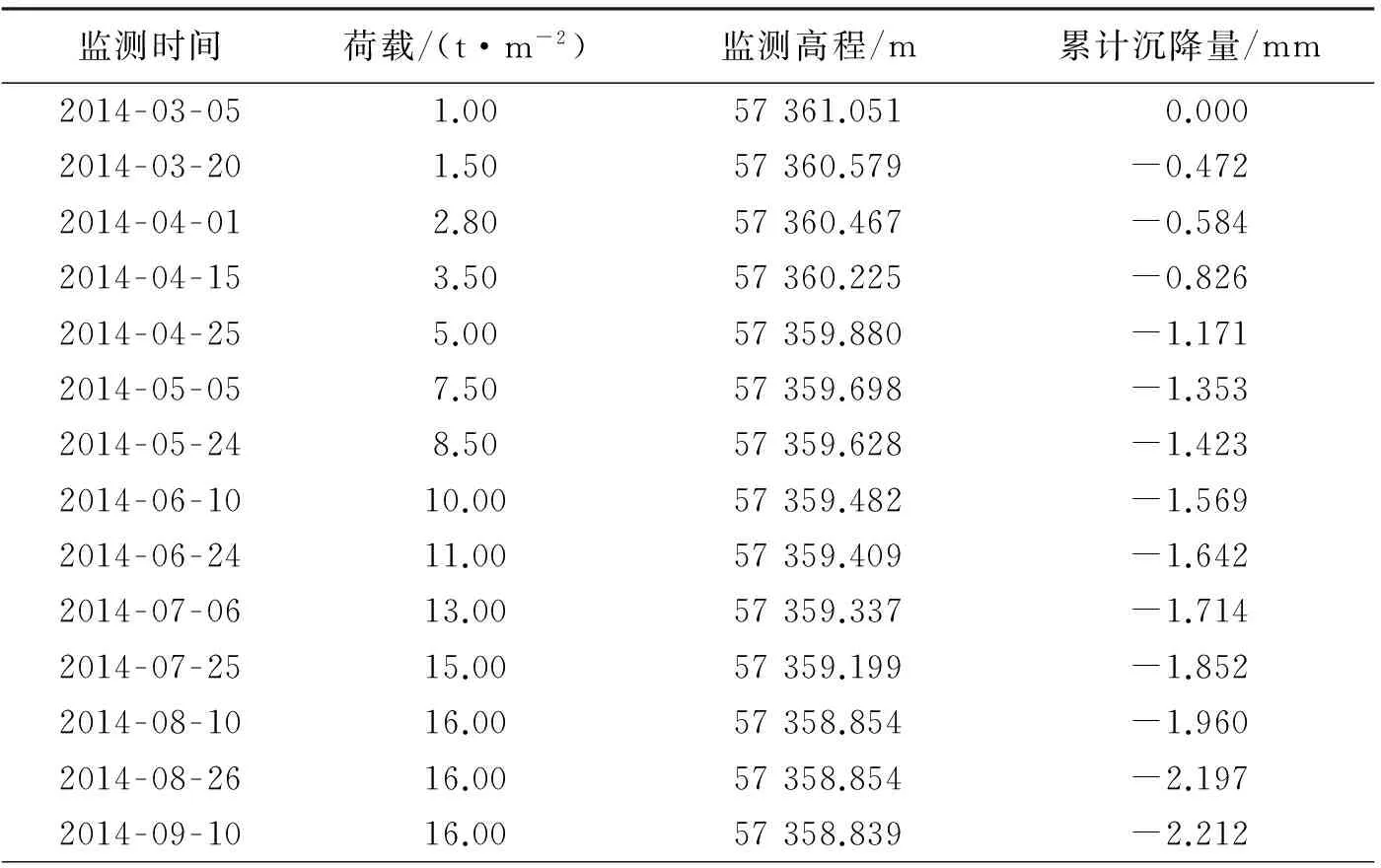
表1　沉降监测点的监测数据

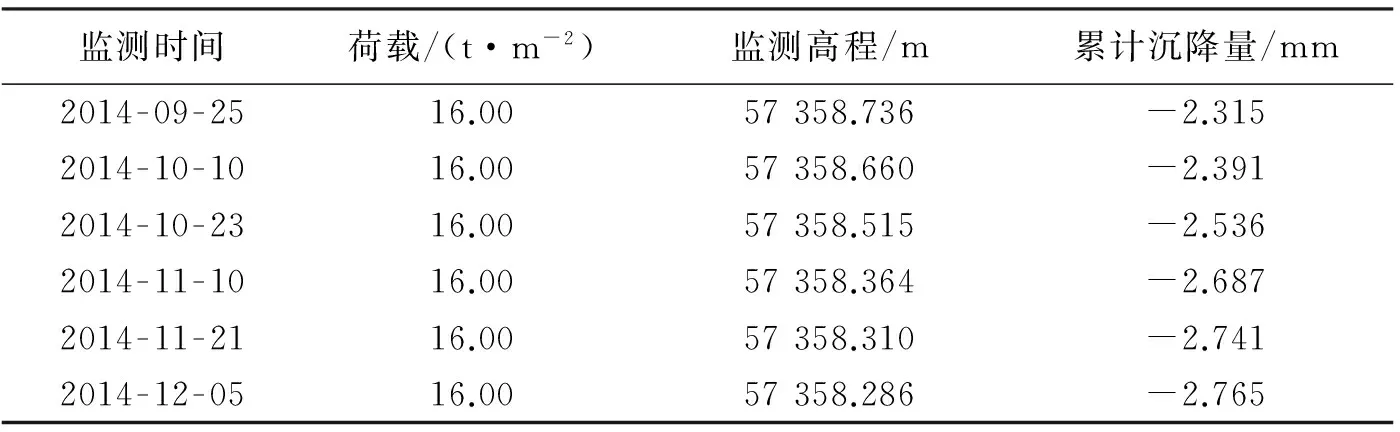
续表

导致建筑物沉降的因素很多，分析表1的数据，可以发现时间间隔与荷载都与沉降有关。

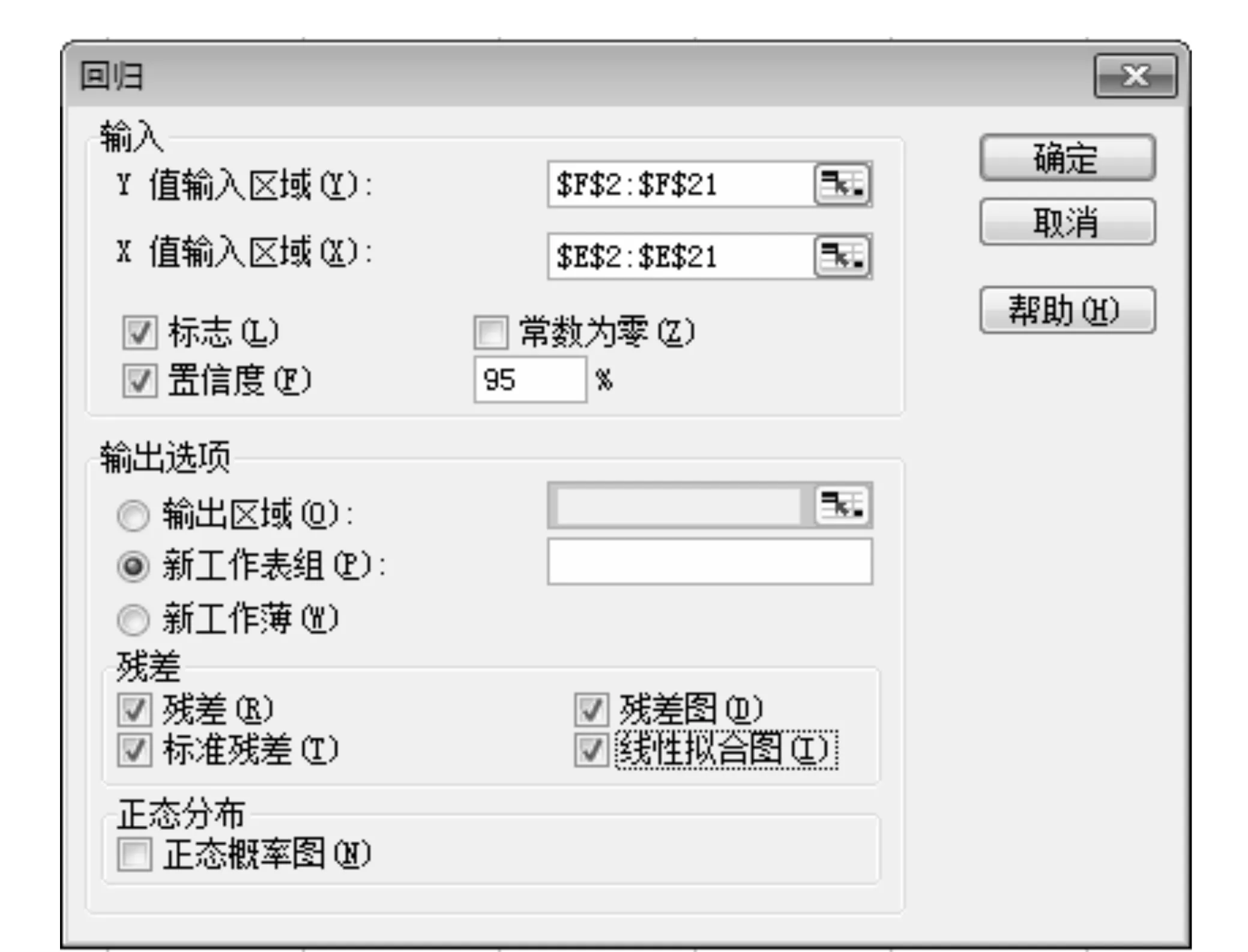
图4　数据输入处理过程

在本文所研究的回归模型中，把影响建筑物沉降的因素(时间间隔和建筑荷载)作为变化因子，带入到多元回归方程中，计算所需要的数据，然后估算沉降量的预测值，得出实际观测和预测值间的残差值。从理论角度为工程建筑的安全和顺利施工提供依据。

本文的工程案例是以某小区的11号楼和12号楼为监测对象，把11号楼的A1点累计沉降量(见表2)作为因变量y，时间间隔和建筑物荷载量作为自变量x1和x2，在Excel工具栏中找数据分析选项(如图4)，选定坐标轴的数据区域范围，进行回归分析得出分析结果(见表3、图5和图6)，最后再进行显著性检验，结合实际测量值得出结论。

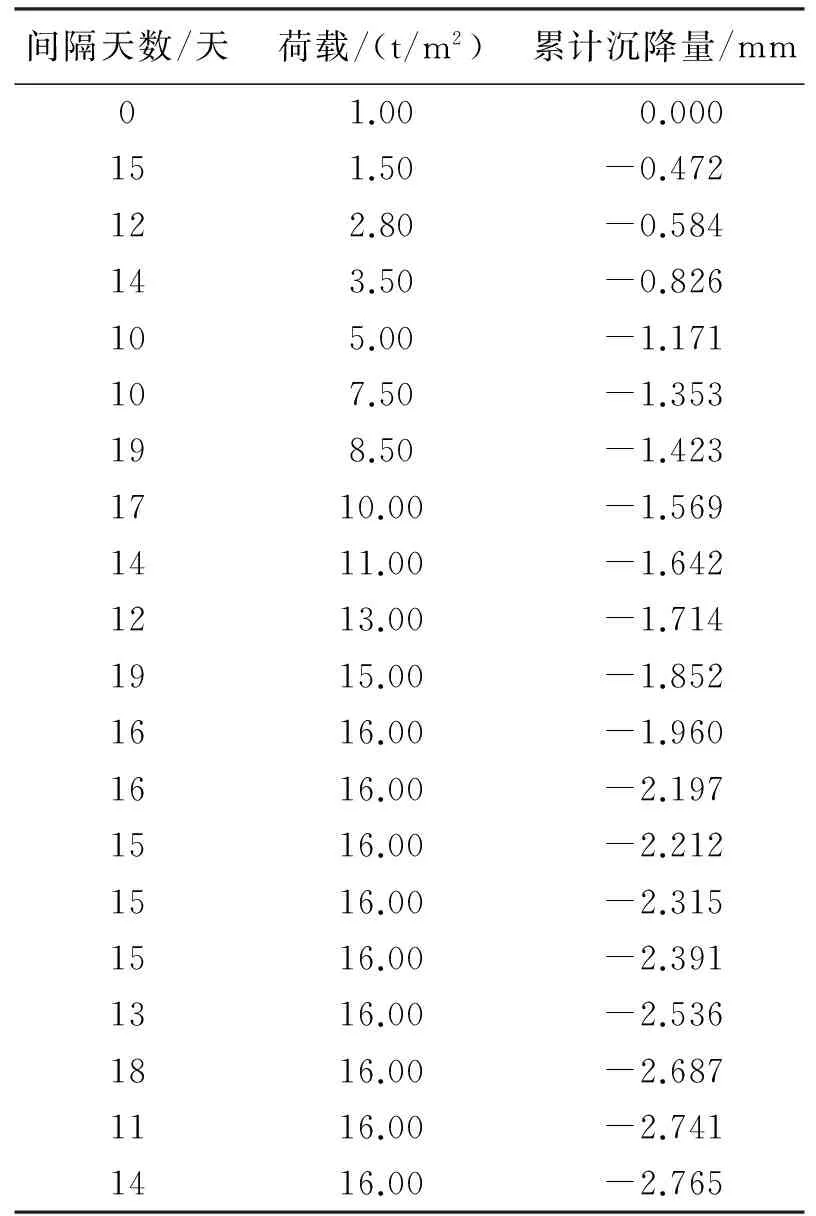
表2　A1点累计下沉量

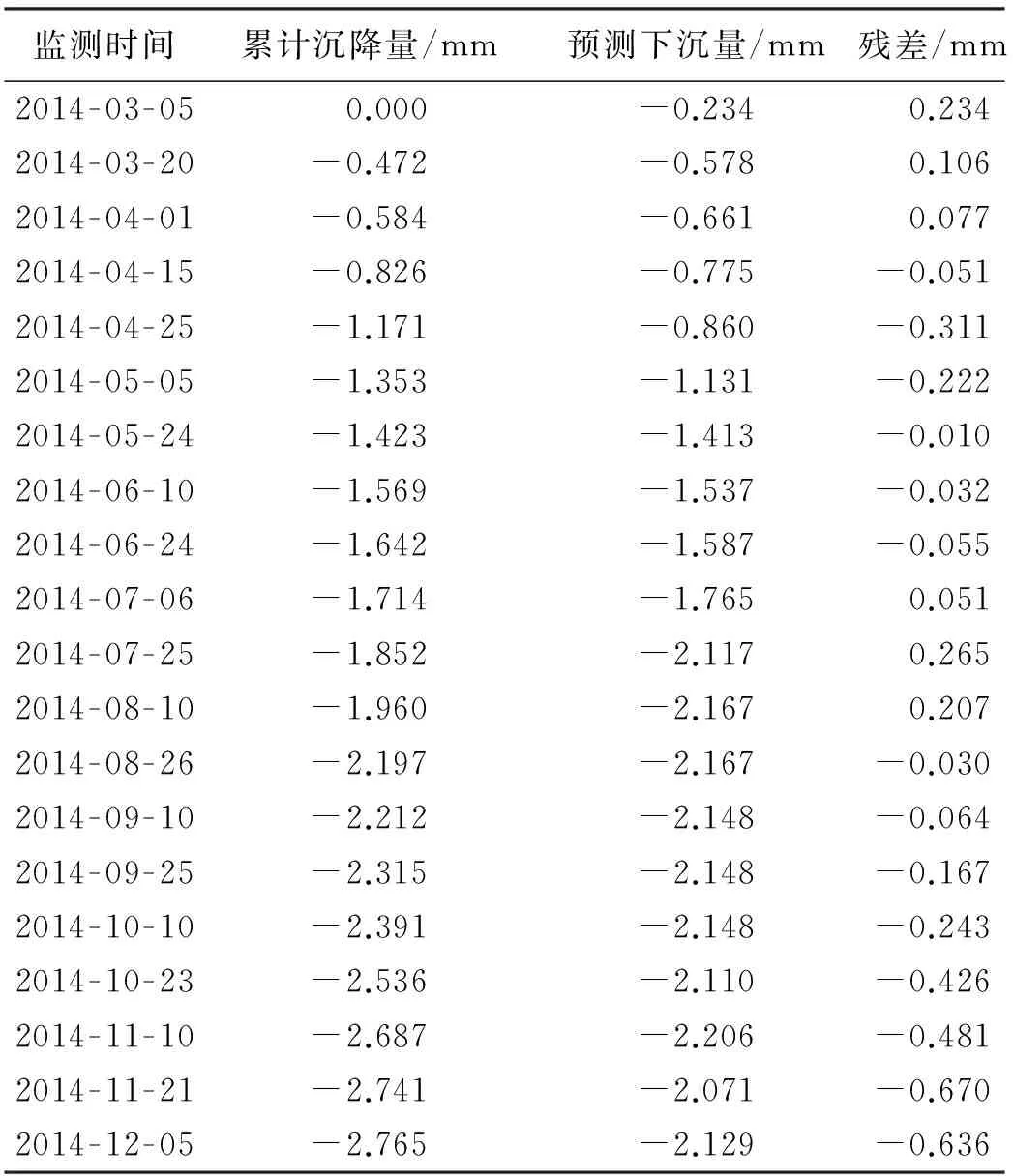
表3　A1点的预测沉降量和残差值

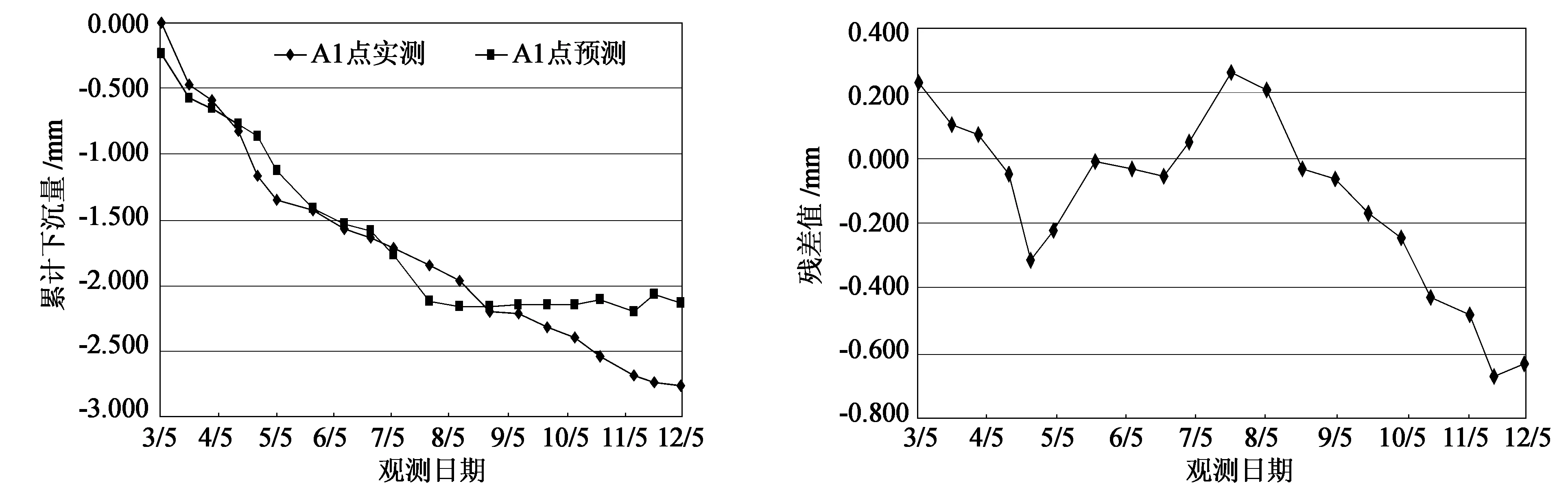
图5　A1点的预测与实测的曲线图　　　　　　　　　　图6　A1点的残差曲线图

4　变形预报与安全分析

观察工程的施工进度，根据沉降量的统计分析规律，实施回归模型的预测和预报，进而整体分析其安全性。由于监测时间和荷载的变化都会导致沉降量值的改变，假设线性关系，从而建立方程：

y=-0.019x1-0.108x2-0.126。

(18)

4.1回归系数的检验(t检验)

解析结果可得出，x1参数所对应的t为-2.585，x2对应的t为-10.918，当α=0.05，由t分布表可得：

(19)

4.2回归方程的检验(F检验)

F统计量101.782，α取值0.05，通过对照F分布表可以得出(k-1)和(n-k)两个不同自由度之间的临界值为

(20)

若临界值小于F的统计量，表明两个自变量都对因变量有着显著性作用。

5　主要结论

回归分析是普遍应用的统计分析与预测技术，本文采取变形数据处理中较为常见的方法，在实验观测数据基础上，借助于建筑物变形要素间的关系，模拟合适的数学模型，再依据模型的数据结果对建筑物进行变形监测预报。通过实例研究处理，得出以下结论：

(1)实现了多元回归分析在变形监测领域的应用，用实例验证了方法的可行性，并且Excel软件的使用使计算结果清晰明了；

(2)应用回归分析可以预测累计变化量，降低事故的发生率，确保建筑物的安全；

(3)回归模型处理数据可以得到良好的拟合度，从而提高结果预测的准确率。

使用回归线性方程对监测对象的累计沉降量进行预测，并与实际沉降量相比较，说明了回归分析法有利于保证建筑物的安全实施，随着安全预报系统、资料分析系统和数据处理系统不断完善，变形监测也需要选取更优化的指标，找出更合理的方案。例如：监测对象类型不同会形成不同的建筑物荷载，采用不同的分析方法建立数学模型是否可以提高预测建筑物沉降的精度等，仍需要更为深入地探索。

[1]颜景生.山东省地面沉降防治研究工作进展及典型区地面沉降规律分析[J].中国人口·资源与境,2014,24(11):194-198.

[2]王世杰,杨国林.工程建筑物变形监测技术研究综述[J].矿山测量,2009(6):74-77.

[3]中华人民共和国建设部.JGJ 8—2007建筑变形测量规范[S].北京:中国建筑工业出版社,2013.

[4]郑箫,金青.回归模型与时间序列在大坝变形监测中的应用[J].湖北师范学院学报:自然科学版,2010,30(1):83-88.

[5]熊成喜.水库移民安置区土地流转规模研究[D].武汉:华中农业大学,2010.

[6]汤少云.大型建筑物沉降变形监测与数据处理[J].科技信息,2013(1):376-377.

[7]赵仲荣,袁树才,张立群.建筑物差异沉降的时间序列与预报[J].工程勘察,2010(1):73-76.

[8]田青.地下水开采造成的地面沉降研究[J].价值工程,2014(33):78-79.

[9]岳建平,方露,黎昵.用时间序列分析法进行建筑物沉降观测数据处理的研究[J].测绘科学,2004,29(6):77-78.

[10]张俊中,宋蕾,张健雄.多元回归分析模型在变形监测中应用[J].河南工程学院学报:自然科学版,2009,21(3):23-25.

[11]杨勇超,李东辉.回归分析模型在大坝变形监测中应用[J].地理空间信息,2011,9(6):137-138.

[12]冯元新.作图法与线性回归法的分析与运用[J].浙江科技学院学报,2004,16(1):5-6.

[责任编辑：魏 强]

Regression analysis of ground subsidence and deformation monitor for buildings

DONG Mi-na,XIE Xiao-ping

(School of Geography and Tourism, Qufu Normal University, Rizhao 276800, China)

Ground subsidence is a common geological hazard, which destroys the ground construction facilities, and it has a profound impact on the environment and urban construction. Through analyzing the factors of land subsidence and the method of monitoring land subsidence and deformation monitoring, a multiple regression model is fomulated. The study hopes to provide theoretical support for the solution to conflict between between land subsidence and groundwater mining by data processing and regression significance test.

deformation monitoring;data processing;regression analysis

1673-2944(2016)04-0086-07

2016-04-08

2016-05-20

董咪娜(1991—)，女，安徽省濉溪县人，曲阜师范大学硕士研究生，主要研究方向为自然地理；[通信作者]谢小平(1966—)，男，甘肃省武山县人，曲阜师范大学教授，硕士生导师，主要研究方向为自然地理、3S技术与应用。

O29:P642.26

A