具有免疫反应的时滞HIV感染模型的稳定性
田海燕, 郭建敏, 郭彩霞
(山西大同大学 数学与计算机科学学院, 山西 大同 037009)
具有免疫反应的时滞HIV感染模型的稳定性
田海燕,郭建敏,郭彩霞
(山西大同大学 数学与计算机科学学院, 山西 大同 037009)
建立了具有免疫反应的时滞HIV感染模型,讨论了系统解的非负性和有界性,得到了确定模型动力学性态的基本再生数。通过构造适当的Lyapunov泛函,利用LaSalle不变原理证明了无病平衡点的全局渐近稳定性,并用数值模拟验证了结果。
病毒感染;全局稳定性;免疫反应;时滞;李雅普诺夫函数
传染病一直是人类身体健康的公敌,传播速度以及对人类生命的威胁程度令人震惊。人类免疫缺陷病毒HIV是一种感染人类免疫系统细胞的慢性病毒,属于反转录病毒的一种。1983年,人类免疫缺陷病毒在美国首次被发现。该病毒破坏人体的免疫能力,导致免疫系统失去抵抗力,从而导致各种疾病得以在人体内生存,发展到最后甚至会导致艾滋病。艾滋病严重地威胁人类的生存,已引起世界卫生组织和各国政府的高度重视,各国在艾滋病的预防、控制及在科学研究上都投入了巨大的人力、物力、财力。艾滋病在世界范围内的传播日渐迅猛,严重威胁了人类的健康和社会的发展,已成为威胁人类健康的第四大杀手。HIV主要攻击人体的辅助T淋巴细胞系统,一旦侵入机体细胞,病毒将会和细胞整合在一起,终生难以消除。因此,建立传染病的动力学模型,研究其发病原因和流行规律,尤其是找寻相应的防治措施和预防策略,已成为当今世界迫切解决的一个重大问题。
国内外诸多学者[1-8]在这方面做了大量的研究。为了描述易感染细胞、感染细胞以及病毒颗粒之间的关系,早在1996年,NOWAK M A等[4]就建立了如下基本的病毒动力学模型:
(1)
其中:x,y,z分别表示易感染细胞的浓度、已感染细胞的浓度以及病毒颗粒的浓度;参数λ表示新的靶细胞的产生率;a表示易感染细胞的死亡率;β是描述感染率的常数;b表示已感染细胞的死亡率;c表示病毒颗粒的产生率;d表示病毒被清除的速率;所有系数为正。
然而要为病毒感染提供更精确的模型,考虑免疫反应必不可少[9-10]。人体内存在多种不同的免疫反应,然而许多研究资料表明,在多种免疫反应中,HIV特异的CTL反应对疾病的发展进程最大,是控制HIV复制和扩散的主要机制。当病毒进入易被感染的细胞后,机体中的巨唾细胞等会首先起作用杀死病毒,然后是CTL免疫细胞和抗体的作用。也就是说CTL免疫细胞的作用至关重要。因此,越来越多的学者开始关注具有CTL免疫应答的HIV感染的群体动力学研究,其中包含CTL免疫应答的最基本的模型如下:
这里z(t)表示CTL的浓度,p表示CTL对已感染细胞的清除强度,k是CTL的死亡率,函数f(x,y,z)描述了感染细胞刺激下CTL产生的速率。假设CTL的产生不仅依赖已感染细胞的浓度,还依赖CTL自身的浓度,于是可取f(x,y,z)=qyz,具体模型为
(2)
模型(2)中,细胞的感染率是以双线性函数βxv的形式给出。
文献[6]建立了如下的时滞动力学模型:
(3)
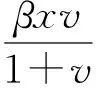
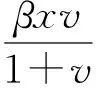
(4)
这里τ表示健康细胞被感染到新病毒产生并释放出来所需要的时间,所有系数均为正数,其他参数与模型(2)有相同的含义。
1 基本性质
模型(4)是一个时滞微分方程系统。设X=C([-τ,0];R4),根据时滞微分方程基本理论,系统(4)在初始条件
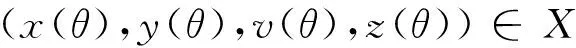
(5)
下存在唯一解(x(t),y(t),v(t),z(t))。
从生物学意义出发,假设初始函数x(θ),y(θ),v(θ),z(θ)均非负,即

(6)
根据泛函微分方程的基本理论,在初始条件(5)、(6)下可得如下结论:
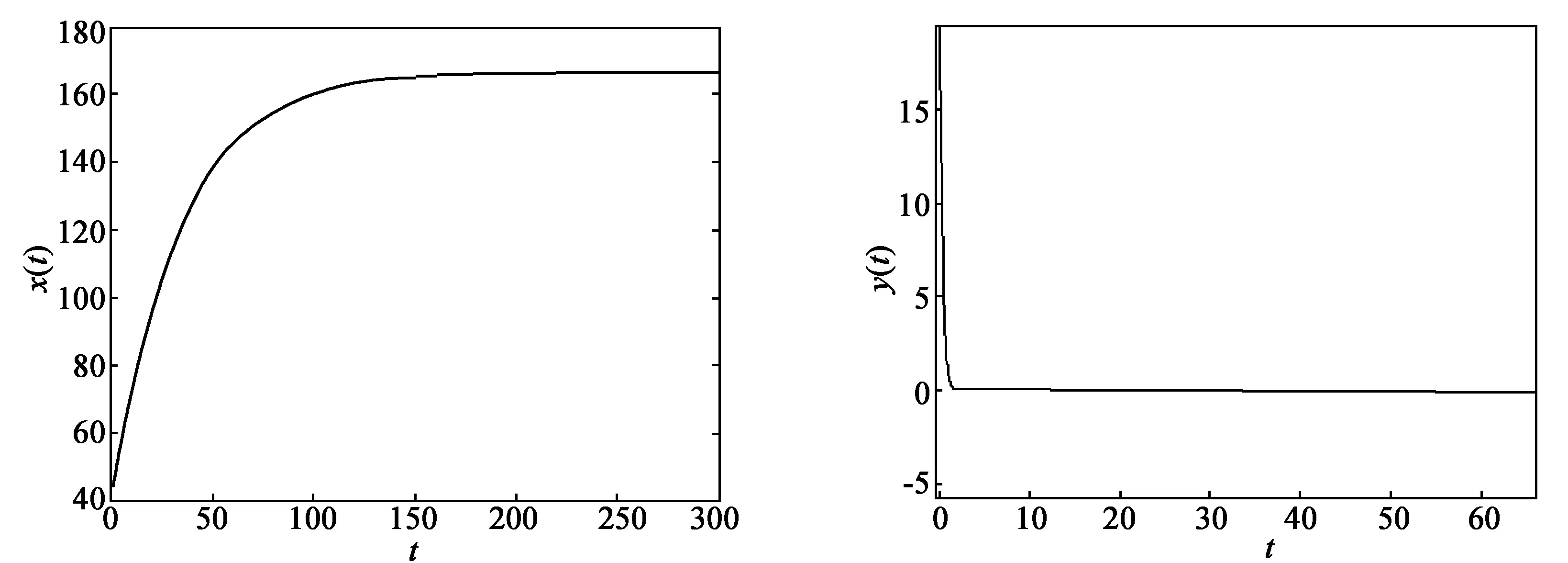
定理1在初始条件(5)、(6)下,系统(4)的所有解都是非负的,并且一致有界,即存在M>0使得x(t) 即 两边从0到t1积分,有 即 同理可解出 若t1∈[0,τ],显然x(t1)>0,y(t1)>0,z(t1)≥0。 定理2当R0<1时,系统(4)的无病平衡点E0=(s/a,0,0,0)是全局渐近稳定的。当R0>1时,无病平衡点E0=(s/a,0,0,0)不稳定。 证明构造Lyapunov泛函: 结合系统(4)有: 下面证明当R0>1时,无病平衡点E0=(s/a,0,0,0)不稳定。系统(4)对应的线性系统在E0=(s/a,0,0,0)处的特征方程为 整理可得 因此无病平衡点的稳定性取决于方程 (7) 记f(λ)=λ2+(b+μ)λ+bμ-cβx0e-(μ1+λ)τ,则当R0>1时, 且 从而方程(7)至少存在一个正根。因此无病平衡点E0=(s/a,0,0,0)是不稳定的。 为了证实定理2的正确性,我们用数学软件MATLAB进行数值模拟。初始条件由健康细胞、感染细胞、病毒颗粒和CTL细胞组成,记为(x0,y0,v0,z0),即初值函数为常值函数,即∀θ∈[-τ,0],有x(θ)=x0,y(θ)=y0,v(θ)=v0,z(θ)=z0。 (a) 未感染细胞x(t)的图形 (b) 已感染细胞y(t)的图形 (c) 病毒颗粒v(t)的图形 (d) CTL的浓度z(t)的图形图1 模拟结果 从图1可以看出模拟结果与定理2的理论结果一致。我们观察到,该系统的轨迹倾向于无病平衡点E0=(166.7,0,0,0),也就是说在这种情况下,没有病毒感染,同时免疫反应和时滞不影响系统的稳定性。 本文讨论了一类具有免疫反应的时滞HIV动力学模型,给出了在给定的初始条件下,模型解的非负性和有界性。最后利用Lyapunov函数方法,应用LaSalle不变原理,证明了当基本再生数R0<1时,无病平衡点全局渐近稳定,并通过数值模拟验证了理论结果的正确性。 [1]李益群,李建全,李琳.一类具有CTL作用的HIV感染模型的全局稳定性[J].生物数学学报,2013,28(3):467-472. [2]LYU Cui-fang,HUANG Li-hong,YUAN Zhao-hui.Global stability for an HIV-1 infection model with Beddington-DeAngelis incidence rate and CTL immune response[J].Communications in Nonlinear Science and Numerical Simulation,2014,19(1):121-127. [3]HUANG Dong-wei,ZHANG Xiao,GUO Yong-feng,et al.Analysis of an HIV infection model with treatments and delayed immune response[J].Applied Mathematical Modelling,2016,40(4):3081-3089. [4] NOWAK M A,BONHOEFFER S,HILL A M,et al.Viral Dynamics in hepatitis B virus infection[J].Proceedings of the National Academy of Sciences,1996(9):398-402. [5]眭鑫,刘贤宁,周林.具有潜伏细胞和CTL免疫反应的HIV模型的稳定性分析[J].西南大学学报:自然科学版,2012,34(5):23-27. [6]郑重武,张凤琴.一类具有感染时滞的HIV模型的稳定性分析[J].数学的实践与认识,2010,40(13):247-252. [7]常侠,袁朝晖.一类具免疫应答和非线性感染函数的时滞HIV-1感染模型的全局稳定性[J].经济数学,2011,28(4):1-5. [8]TIAN Xiao-hong,XU Rui.Global stability and Hopf bifurcation of an HIV-1 infection model with saturation incidence and delayed CTL immune response[J].Applied Mathematics and Computation,2014,237(7):146-154. [9]陈美玲.具免疫应答的时滞HIV感染模型动力学性质研究[D].衡阳:南华大学,2010. [10]曹艳红.具有免疫应答和细胞内部时滞的HIV感染模型的稳定性分析[D].衡阳:南华大学,2011. [责任编辑:魏 强] Stability of a delay HIV infection model with immune response TIAN Hai-yan,GUO Jian-min,GUO Cai-xia (School of Mathematics and Computer Science, Datong University, Datong 037009, China) In this paper, we built a delay infection model with immune response and discussed the nonnegativity and boundedness of the solution. The basic reproduction number is obtained, which determines the dynamical behaviors of the infection model. By constructing suitable Lyapunov functions and applying LaSalle’s invariance principle we have proven that the infection-free equilibrium is globally asymptotically stable. Then numerical simulations are carried out to support the result. virus infection;global stability;immune response;delay;Lyapunov function 1673-2944(2016)04-0080-06 2016-04-09 2016-06-12 国家自然科学基金资助项目(11301312);山西大同大学青年科学基金资助项目(2014Q10);山西大同大学科学基金资助项目(2015K5) 田海燕(1984—),女,山西省朔州市人,山西大同大学助教,硕士,主要研究方向为微分方程;郭建敏(1971—),女,山西省大同市人,山西大同大学教授,硕士,主要研究方向为微分方程;郭彩霞(1981—),女,山西省大同市人,山西大同大学讲师,硕士,主要研究方向为泛函分析。 O175.13 A
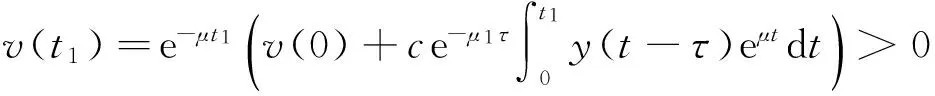
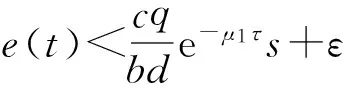
2 无病平衡点的稳定性分析
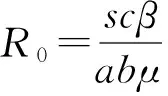
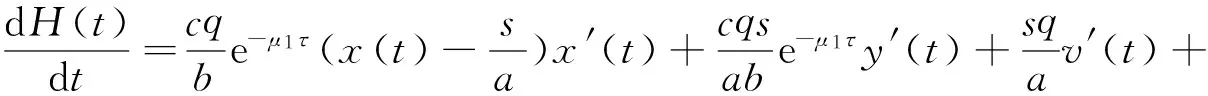


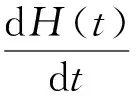

3 数值模拟


4 结 论

