山区河流微弯河段平面二维数值模拟应用研究

陈杏文，　颜雪丽

(1.重庆交通大学 河海学院， 重庆 400074；2.夹江县水利水产服务中心， 四川 夹江 614100)



山区河流微弯河段平面二维数值模拟应用研究

陈杏文1，颜雪丽2

(1.重庆交通大学 河海学院， 重庆 400074；2.夹江县水利水产服务中心， 四川 夹江 614100)

数值模拟技术在河道整治中的应用越来越广泛，利用通用商业软件以及自编程序进行计算是目前主要的两种数值模拟方法。针对长江上游微弯河段河道特性，对丰都刀鞘溪河段进行数值模拟，复演河段的水位与流动情况。通过对比发现计算水位与实测水位偏差很小，河道流动情况与实测流动情况大致相同，达到了较高的计算精度，能够满足工程应用的需求，较好地模拟了复杂的河道流动情况。计算成果可用于长江上游通航、行洪论证以及航道整治等方面研究。

数值模拟；河道整治；Fortran程序

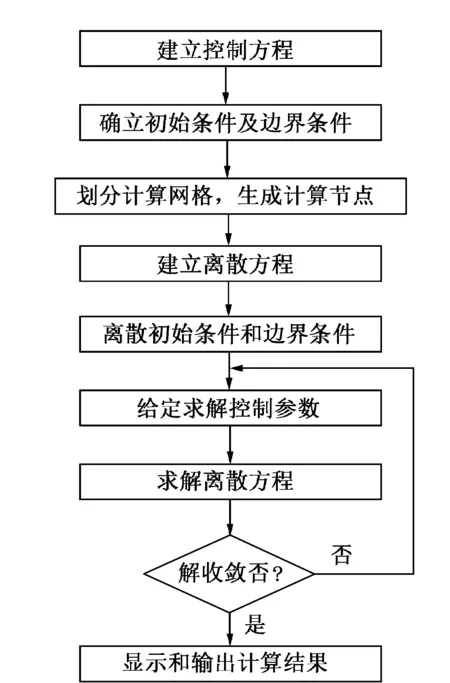
图1　CFD计算流程图

数值模拟技术已广泛应用于航道的工程整治技术中，并发挥着越来越大的作用。二维水流数学模型克服一维水流数学模型无法模拟水流沿横向(河宽方向)、垂向(水深方向)变化的不足，较好地模拟了平面流场，因此在工程上应用较为广泛。同时，物理模拟为数值模拟提供边界条件以及验证数据，数值模拟为更加准确地进行物理模拟提供了前提条件[1]，二者一起使用相互补充、相互验证。

在我国，吴修广等[2]采用Laplace方程坐标变换方法生成正交曲线网格，并对浅水流动的控制方程进行坐标变换，采用B型交错网格，用SIMPLEC算法解非正交曲线坐标下的k-ε双方程紊流模型，修正了由网格的非正交性引起的误差。沈永明[3]对浅水流动的控制方程进行坐标变换，导出了非正交曲线坐标下平面二维水流计算的代数应力模型公式，建立了非正交曲线坐标下平面二维水流计算的代数应力湍流模型。李大鸣[4]采用有限体积法建立了适应河道、滞洪区复杂情况的洪水演进一、二维衔接数学模型，可以较好地模拟复杂流域的洪水演进过程。窦亚军[5]则利用Fortran语言编制程序建立了数学模型模拟溃坝。

二维数值模拟的基本思路如图1所示[6]。本文针对长江上游微弯河段的水流流动特性，结合具体实例利用Fortran语言编制计算程序，探讨长江上游河段二维平面数值模拟的应用，为后续数值模拟研究与工程技术应用提供更多的思路与方法。

1　数学模型的建立

1.1控制方程

为了复演长江上游河段水流流动情况，需求解二维完全圣维南方程组，进而求出计算时间内整个研究区域的水位、流量及二维X、Y方向的水流速度。考虑到长江上游微弯河道的流动情况，这里并不考虑热交换以及湍流附加方程，仅选择连续方程与动量方程作为基本控制方程，具体见公式[7]：

水流连续方程

(1)

X方向动量方程

(2)

Y方向动量方程

(3)

以上各式中，t为时间；u，v分别为沿X，Y方向的流速；h为水深；a为床面高程；g是重力加速度；f为科氏参数；εxx，εyy，εxy是紊动粘性系数，取为αu*h，α=3～5，h为水深，u*为摩阻流速。

1.2网格生成

采用数值方法求解控制方程时，必须将控制方程在空间区域进行离散，然后求解得到离散方程组。要想在空间域上离散控制方程，必须确定网格形式。而对于不同的问题采用不同的数值解法时，采用的网格也是不同的，一般计算网格可划分为结构网格与非结构网格两大类，而网格划分的质量也决定了计算的精确性，同时考虑到山区河流边界地形条件非常复杂，致使坐标系的选取及网格划分难度增加[8]。本文采用贴体正交坐标系下的平面二维水流数学模型，其离散网格如图2所示，该二维水流数学模型能较好地模拟复杂的河道边界条件[9-10]。

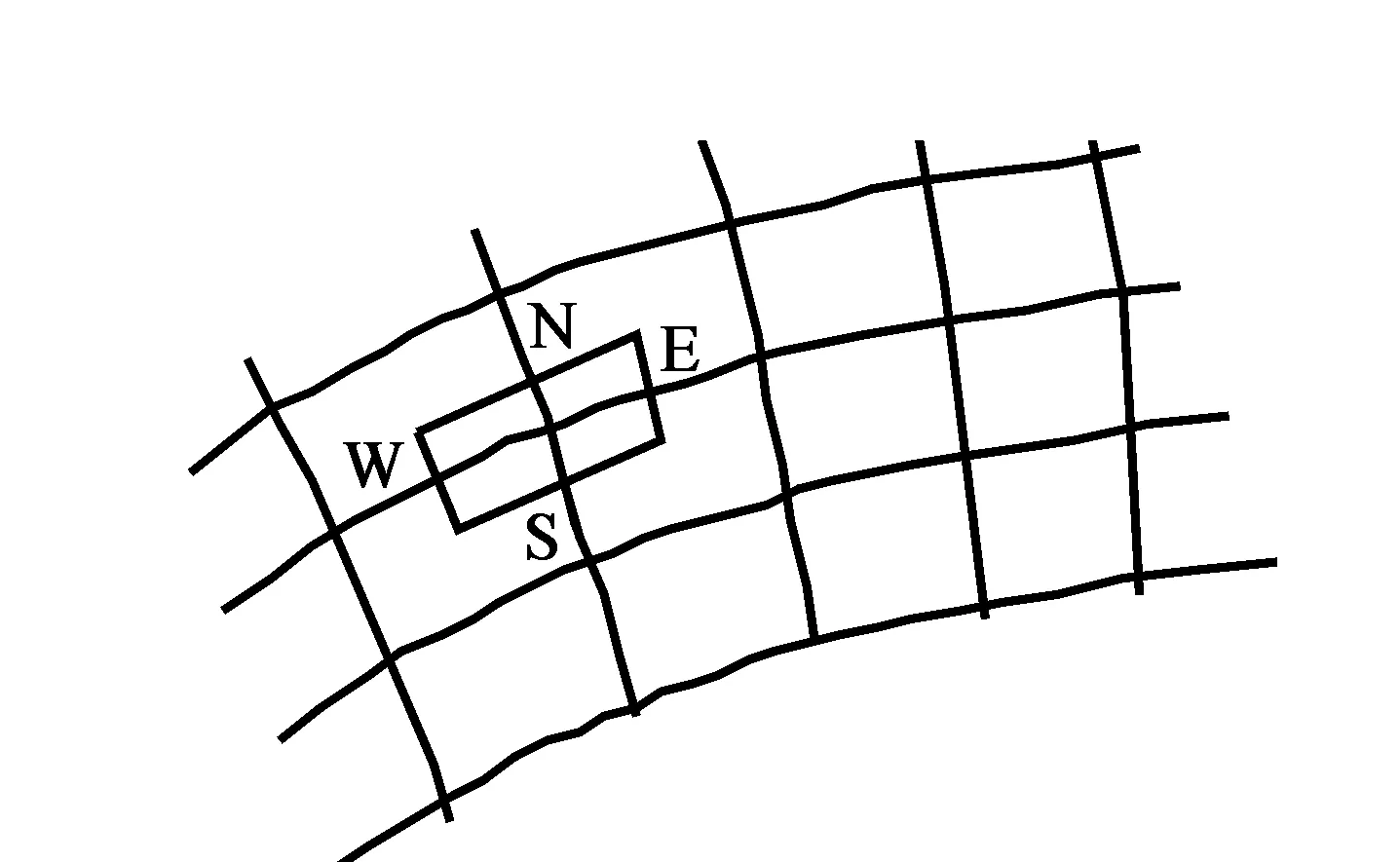
图2　数模网格示意图

1.3边界条件与控制参数

给定的边界条件包括：入口边界的流量，出口边界的水位或水位流量特征曲线。另外还应根据研究区域的实际情况对抽排水、风场及风暴等边界条件进行定义。模型中的主要参数包括:糙率、紊流交换系数、干湿单元及风场等。河床糙率反应了河床的摩擦阻力，具体边界条件如下[11]：

(1)初始条件

对于给定的研究域，在时间t=0时有

(4)

(5)

(6)

其中h0为初始时刻的水深,r0,s0为初始时刻的流量分量。

(2)边界条件

岸边界：该边界为非滑移边界，即u=0，v=0。

进口边界：进口边界位于计算河段的进口断面，其ξ方向给定入流单宽流量沿断面的横向分布，即u(η)·h(η)=f(η)，并给定∂v/∂ξ=0。进口、出口断面一般布置在顺直、单一、无回流等特殊流态的河段。

出口边界：计算河段的出口断面给定水位沿河宽的分布，同时给定流速边界条件

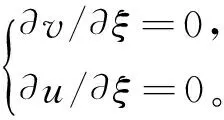
动边界：根据网格节点处河底高程和水位，可以判断该网格单元是否出露水面，若不出露，糙率值采用正常值；若出露，则出露网格点做不参与计算的处理。

2　计算实例

2.1工程概况

计算河段位于丰都县城区丰都长江大桥上游3.2 km湛普镇白水村一组朱家嘴河段，下距龙河与长江交汇口约10.4 km，水路上距重庆约168 km，顺长江岸线的航道里程为492 km左右，河段河势如图3所示。该河段位于三峡水库常年库区内，计算河段下游设有白沙沱水位站，上游的涪陵清溪场水文站为国家一类水文站，因此，工程河段的水文泥沙情况受三峡水库调度及长江清溪场水文站和白沙沱水位站控制。本文所做验证的计算资料如下：

(1)工程河段河床地形图(2007年11月测图，比例：1∶2 000)；

(2)工程河段实测水面线及流速流向(2008年8月13日施测，Q=32 600 m3/s)；

(3)尾水位设置为151.6 m(吴淞高程)。

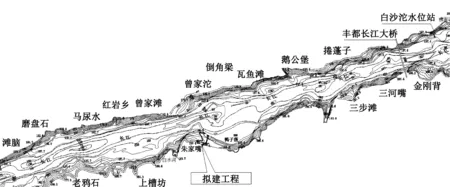
图3　工程河段河势图

2.2计算网格的生成

根据工程所处位置并考虑计算需要的进出口长度、实测验证资料位置，选取计算河段长度约11 km。在计算域内共布置500×60个网格点，经正交计算后得到正交网格图，网格线的交角除岸边个别节点以外均为88°～92°，基本保持正交。正交曲线网格沿河流方向间距为20～30 m，沿河宽方向间距为20～30 m。

2.3边界参数

为了使研究成果更加可靠，本实例同时采用商业软件进行计算比对，根据试算与率定，模型关键参数设置如表1所示。

3　结果与讨论

利用所编制的程序，可以计算出在限定情况下各点的水位、流速。河道水位模拟情况见表2。

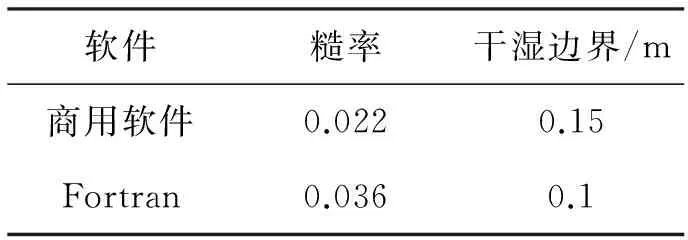
表1　二维模型关键参数比对

根据表1和表2中计算值与实测值的差值可以看出，无论商业软件计算还是Fortran自编程序计算值与实测值的差值均在-0.1～0.1之间，较好地模拟了该河段的水位情况。

两种数值模拟方法下流速值的偏差可见表3。

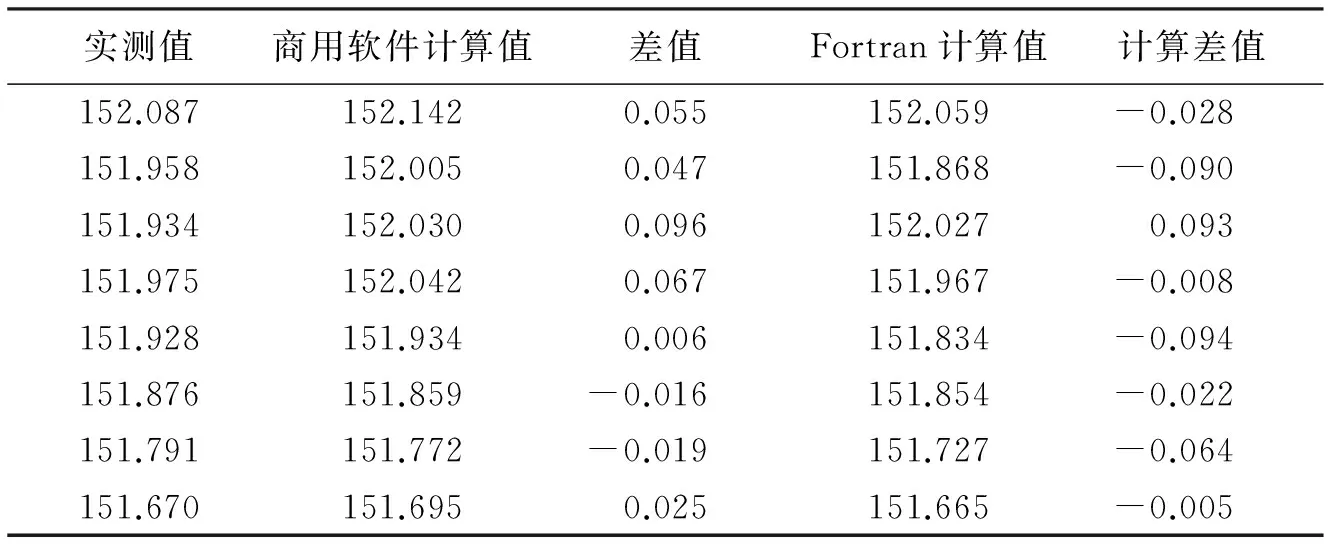
表2　水位差值/m

表3　流速差值

由表3可以看到，选取的实测断面流速与计算流速值整体看偏差不大，商业软件计算偏差在±0.3 m/s之内，自编程序差值在±0.2 m/s以内，数值模拟的精度符合工程建设的需求，同时比对Q=23 200 m3/s和Q=40 640 m3/s两级流量下局部河段的流场图(见图4)可以发现，计算得出的河道流动情况与实测流动情况大致相同。可以利用该程序对长江上游河段进行流场模拟，为长江上游顺直与微弯河段的航道通航、行洪论证提供技术支持。

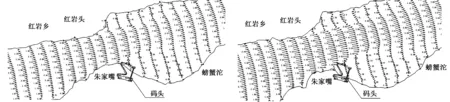
(a) Q=23 200 m3/s　　　　　　　　　　　　　　　　(b) Q=40 640 m3/s　图4　局部河段流场图

4　结　论

(1)针对长江上游微弯河段河道特性，对丰都刀鞘溪河段进行二维平面数值模拟计算，通过商业软件与自编程序均能达到很好地复演河段的水位与流动情况，在达到相同计算精度的情况下，两种方法所设置的关键参数不完全相同。

(2)两种计算方法结果均具有计算精度高、速度快的特点，模拟结果显示河道流动情况与实测流动情况大致相同，可以将该计算成果用于长江上游航道通航安全论证、行洪论证以及航道整治等方面研究工作中。

[1]于曰旻.正交曲线坐标系下复杂边界二维水流数值模拟研究[D].大连：大连理工大学,2006.

[2]吴修广,沈永明,郑永红,等.非正交曲线坐标下二维水流计算的SIMPLEC算法[J].水利学报,2003(2):25-30.

[3]沈永明,吴修广,郑永红.曲线坐标下平面二维水流计算的代数应力湍流模型[J].水利学报,2005(4):383-390.

[4]李大鸣,林毅,徐亚男,等.河道、滞洪区洪水演进数学模型[J].天津大学学报:自然科学与工程技术版,2009,42(1):47-55.

[5]窦亚军.溃坝洪水波数值方法研究[D].重庆：重庆交通大学,2009.

[6]王福军.计算流体动力学分析：CFD软件原理与应用[M].北京：清华大学出版社,2004.

[7]章梓雄.粘性流体力学[M].北京：清华大学出版社,1998.

[8]李艳红,周华君,时钟.山区河流平面二维流场的数值模拟[J].水科学进展,2003，14(4):424-429.

[9]余利仁,许卫新,张书农.正交贴体坐标系的生成[J].河海大学学报,1988,16(5):78-85.

[10]杨胜发,尤田,刘岩.双连通域正交坐标系的生成[J].重庆交通学院学报,2001,20(增刊1):127-130.

[11]陈勇康,胡江,宋丹丹,等.长江铜锣峡河段炸礁整治数学模型计算及验证[J].水运工程,2015(6):131-136.

[责任编辑：李 莉]

Application research of simulation for micro-bend reach of mountain river by using 2D numerical model

CHEN Xing-wen1,YAN Xue-li2

(1.School of River & Ocean Engineering, Chongqing Jiaotong University, Chongqing 400074, China；2.Water Conservancy and Aqriculture Service Center of Jiajiang County, Jiajiang 614100, China)

The application of numerical simulation technology is more and more widely used in the area of river regulation. The use of general commercial software and the self-designed program are the two main kinds of numerical simulation methods now. According to the characteristics of micro bend reach on the upstream of the Changjiang river, the Fengdu Daoqiaoxi reach is simulated by using numerical model to simulate the water level and velocity of that reach. The calculation result shows that the deviation of calculated water level and the measured water level is very small, meanwhile the simulated flow situation and the measured flow situation is almost the same, which achieves great calculation accuracy, and therefore can meet the need for engineering application. The results can be used to do the navigation and flood demonstration, river regulation and other kinds of research work in the upper reaches of Changjiang river.

numerical simulation;river regulation;Fortran

1673-2944(2016)04-0029-05

2016-02-26

2016-04-25

陈杏文(1990—)，男，广东省梅州市人，重庆交通大学硕士研究生，主要研究方向为航道整治及河道治理。

U611

A