广义确定性均匀递归树网络的拉普拉斯谱

赵虎

（青海师范大学 计算机学院，青海 西宁　810008）

广义确定性均匀递归树网络的拉普拉斯谱

赵虎

（青海师范大学 计算机学院，青海 西宁810008）

在复杂网络的模型构建与性质研究领域中，确定性均匀递归树网络模型DURT（Deterministic Uniform Recursive Tree）得到了广泛应用。在DURT网络模型的基础上提出一种适用范围更广的广义确定性均匀递归树演化模型GDURT（Generalized Deterministic Uniform Recursive Tree），通过设计一种能够真实反映网络增长演变特点的最优节点分层编号方法，结合代数化简，找出了能够快速计算GDURT网络的拉普拉斯特征值和特征向量递推关系式，并对GDURT网络的拉普拉斯谱性质做了分析。

复杂网络；演化模型；确定性均匀递归树；广义；节点分层；拉普拉斯谱

复杂系统在现实世界中普遍存在，受制于其庞大的系统规模和各项系统要素之间的复杂关系，人们对复杂系统的结构、性质以及二者之间的相互作用机理的了解十分有限［1］。而确定性模型的建模和性质研究在复杂系统研究领域中充当着十分重要的角色。

在复杂系统建模研究中，确定性模型的主要优势在于它们的拓扑属性可以用分析的方法进行精确计算，其邻接矩阵和拉普拉斯（Laplacian）矩阵的谱性质可以对网络的全局结构进行全面而准确的度量，任何局部性质的改变都能通过谱的变化体现出来。在确定性模型建模研究中，均匀递归树（URT）模型在流行病传播、中世纪家族宗谱树、链锁信、金字塔营销网等领域的研究中得到了成功的运用［2-3］，并逐步延伸到经济学领域中［4］。2008年，章忠志等人在复杂网络的视角下对确定性均匀递归树模型（DURT）作了详尽的分析，准确计算得出了确定性均匀递归树的度分布、平均路径长度、介数分布、度相关性，等拓扑属性，并且得出了其Laplacian矩阵的特征值和特征向量的递推关系［5］。2012年，陆哲明等人在DURT模型的基础上构造出一个小世界网络two-tree network［6］，并对其主要的几个拓扑属性作了深入研究。

在以上研究结果的基础上，对文献［5］中的确定性均匀递归树网络模型作了推广，提出了一种推广的确定性均匀递归树网络模型GDURT（Generalized Deterministic Uniform Recursive Tree），赋予该模型一种更加复杂的演化模式，以期使其具有与现实复杂系统更为接近的特征。通过对GDURT模型在不同时步下的拉普拉斯矩阵结构变化规律分析的角度入手，运用代数方法，寻找一种最优的分层节点编号规则，大大简化矩阵的运算，从而给出了其拉普拉斯特征值和特征向量的递推关系，并对其谱性质作了分析。其中所提出的最优分层节点编号方法不但适用于传统均匀递归树网络模型，对确定性类树复杂超网络的拉普拉斯谱分析也同样适用。

1　GDURT演化模型及其拓扑性质

推广的确定性均匀递归树（GDURT）是通过一个逐次迭代的过程建立的。用t表示网络构建的时步数，用ut表示经过个t时步后建立的GDURT网络，则网络的构建过程为：当t=0时，U0由一个孤立点构成；当t≥1时，Ut通过在Ut-1网络中的每个节点上粘接一条长为l（l≥1）的路构成；这一过程不断重复进行。GDURT网络模型的构建过程由图1所示。

图1　GDURT网络模型构建过程Fig.1　Construction process of GDURT network model

令Ut表示t（t≥0）时步得到的GDURT网络，Nt表示t（t≥0）时步网络Ut的节点总数，并且令ne（t）和nv（t）分别表示在t时步新加入的节点数和边数。已知nv（0）=N0=1，根据模型迭代过程可知：

度分布是研究网络拓扑特性的一项重要参数。网络节点i的度是指节点i的邻居节点的个数。网络的累积度分布Pcum（k）则是指在网络中任意选取一个节点，其度均大于或等于k的概率［3］。网络的平均路径长度d¯t是指网络在t时步时所有节点对之间最短路径长度的平均值。在作者前期研究中得到了GDURT网络的累积度分布和平均路径长度如式（3）、（4）所示。

这意味着GDURT网络的累积度分布随着节点度k呈指数规模递减，是一个指数类型的网络。当网络规模无限增大时，其平均路径长度是按照网络规模Nt的对数关系递增的。网络节点数急剧增多时其平均路径长度增速平缓，具有明显的小世界网络特点［7］。

GDURT网络演化过程中的度相关性knn（k）近似为关于k的线性关系，说明该网络模型是协调的［8］，在每一个时步，新加入到网络中的节点优先与度较大或具有相同度的节点连接。

2　GDURT网络的拉普拉斯特征值和特征向量

令表Vt示网络Ut的节点集合，即：Vt=｛v1，v2，…v（1+l）t｝。网络Ut的邻接矩阵定义为一个（1+l）t×（1+l）t矩阵At=（aij），其中当vi和vj相邻时aij=1；否则aij=0。令dvi表示点vi的度，令Dt=diag（dv1，dv2，…dv（1+l）t）为网络Ut的度对角矩阵。则网络Ut的拉普拉斯矩阵定义为：Ut的特征多项式Pt（ut，λ）定义为：

由定义可知Lt是一个实对称矩阵，所以（1+l）t其个特征值均为实数，假定它们按升序排列：

λ1≤λ2≤L λ（1+l）t。由于Ut是树，所以λi=-λ（1+l）t-i+1。对于一般网络，计算其拉普拉斯特征值及关于特征值的特征向量是NP-困难的［8］，但对于结构较为特殊的网络，只要给节点施以合理的编号，并适当地运用代数化简，便可大大简化矩阵运算，准确求出其特征值和特征向量的分布情况。

2.1拉普拉斯特征值

为了便于矩阵和行列式化简及计算，通过对GDURT模型演化过程的分析，可设计一种针对网络中各个节点的分层编号方法，使得编号顺序按照网络增长过程中节点增加的先后次序排列，并使结构特点相似的节点位于同一分层中。假设当l=2时，分别对t=2和t=3时步的网络实施节点分层编号的过程如图2所示。

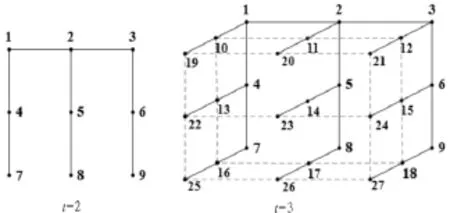
图2　当l=2时，对t=2，t=3时步网络中的节点实施分层编号Fig.2　Hierarchical numbering to nodes of the network wherel=2 and t=2，t=3 respectively

为便于讨论，可将演化过程中t-1时步得到的网络中的节点称作“旧节点”，将t时步得到的网络中新加入的节点称作“新节点”，采用分层编号方法可以使得t时步网络中的Nt-1个旧节点只与个Nt-1新增节点相邻，且这些相邻的新增节点都位于同一层中；对于新增加的Nt-Nt-1=（1+l）t-（1+l）t-1个节点，其最外层节点的度均为1，中间各层的节点度均为2，由此可知，按照分层编号后得到的网络Ut的邻接矩阵具有如下结构特点：

式（7）中，At-1为网络Ut-1的邻接矩阵，It-1为（1+l）t-1阶单位矩阵。由于采用节点分层编号，网络Ut的旧节点只与（1+l）t-1个新节点相邻，新增最外层节点也只与（1+l）t-1个其他新节点相邻，故式（7）中第一行、第一列、最后一行和最后一列中分别只有一个分块矩阵It-1；此外，其余新增中间层节点的度均为2，使得式（7）中除第一行、第一列、最后一行和最后一列的其余各行、各列均含有两个分块矩阵It-1，其余位置上均为0。

对网络Ut的度对角矩阵Dt，需同样遵守上述节点编号规则，不难看出GDURT网络在t时步的拉普拉斯矩阵Lt为：

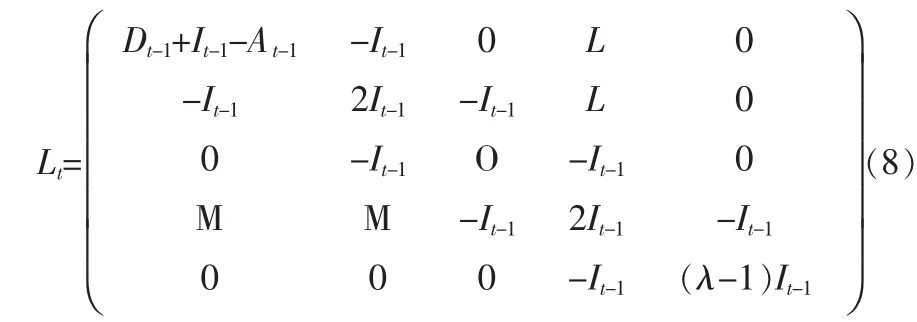
进而可得出GDURT网络在t时步的拉普拉斯特征多项式Pt（Ut，λ）：

式（9）中S=det（λ-1）It-1-Dt-1+At-1，也即t-1时步的网络Ut-1的特征多项式。

运用拉普拉斯展开定理［9］对式（9）进行化简。先由式（9）的第l+1列乘以-1/（λ-1），加到第l列上，再按照第l+1行展开，再以第l列乘以-（λ-2）-1/（λ-1），加到第l-1列上，并按照第l行展开……，依此进行，直到行列式化为最简形式，可得：

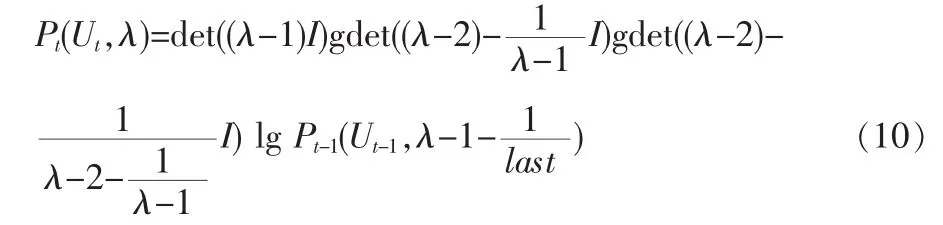
式（10）等式的系数为l个（1+l）t-1阶行列式的乘积，其中符号last表示系数中第l个系数行列式的值。若令α=（1+l）t-1，并作如下符号定义：

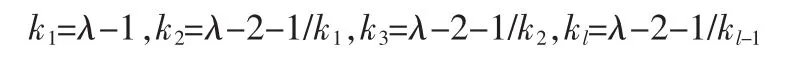
已知对于t-1时步的网络有（1+l）t-1个特征值，而t时步有（1+l）t=（1+l）t-1g（1+l）个特征值；假设网络在t-1时步的特征值用集合△t-1=，，L，｝表示，并假定这些特征值按照升序排列：则（10）式可写为：

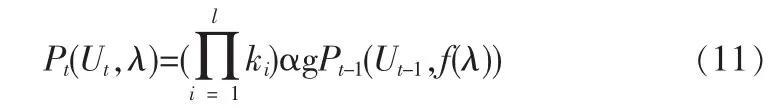
由式（11）可看出：对于t-1时步网络Ut-1的任意一个特征值，方程λ-1-=的解恰好为t时步网络中与特征值对应的1+l个新特征值。由之前关于符号kl的定义以及式（11）可知，方程λ-1-=的实数解恰好为1+l个。为便于讨论，不妨假设l-1，在这种情形下，式（11）变形为式（12）：

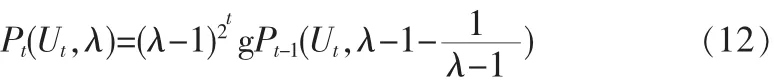
已知t-1时步网络的拉普拉斯特征多项式具有如下形式：

其中qi代表多项式系数。将带入式（13），可以看出形如的项只能出现在项中，且该项系数为1。即，1是多项式Pt（Ut，λ）的常数项，且拉普拉斯特征值中不包含1。

已知树的拉普拉斯特征值均大于或等于0，很容易观察出式（14）、（15）均为单调递增函数，且式（14）总是小于1的，而式（15）总是大于或等于2的，因此，对于t-1时步的任意一个特征值，<永远成立。

当t=1，2，3时的特征值如图3所示。

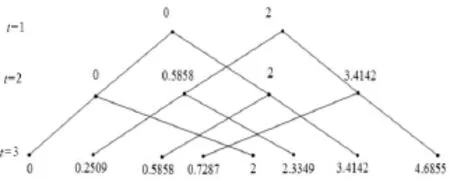
图3　当l=1，t=1，2，3时网络的拉普拉斯特征值分布Fig.3　Laplacian eigenvalue distribution of network where l=1 andt=1，2，t=3 respectively

当l取较大的值时，其f（λ）的表达式将更加复杂，但仍为一个最高次为1+l次的多项式，通过其拉普拉斯特征值的递推关系计算任意时步的特征值均可在关于1+l的多项式时间内完成。

2.2拉普拉斯特征向量

与特征值的计算类似，推广的确定性均匀递归树网络的拉普拉斯特征向量之间也存在着递推关系。假设l=1、λti为t时步网络Ut的任意一个特征值，并假设与特征值λti对应的特征向量为vti，则有如下关系式成立：

其中v1和v2为向量vti的两个2t-1阶分量，均为阶单位矩阵。将式（16）中的向量v1和v2看作未知数展开线性方程组，可得如下关系式：

由式（12），（14），（16）和（18）可知，若将特征值λti代入方程中，则有

已知网络在时t=1，l=1GDURT网络的特征向量为（1，1）T和（1，-1）T，根据式（19）便可递推出任意时步网络的拉普拉斯特征向量，其结果与文献［5］中的特例结论完全一致。

当l取不同值时，其拉普拉斯特征向量的递推关系与此类似。由式（19）可知，任一时步下关于网络的某一个拉普拉斯特征向量，其第一分量总是由上一时步网络中的对应特征向量组成，利用这一现象可进一步减少特征向量的计算时间。

3　结　论

传统的递归树（URT）和均匀递归树（DURT）网络演化模型的提出，为复杂网络确定性演化模型的构建及其相关性质研究研究奠定了坚实的基础，但是相对过于简单的演化过程得该模型的应用受到了一定的局限［3］。文中所讨论的推广确定性均匀递归树模型（GDURT）可应用于与URT网络类似的仿真模拟实验或实际模型的研究中，并具有更强的灵活度和适应性。

通过设计一种能够真实反映网络增长演变特点的最优分层节点编号方法，可有效减少原本NP-难的拉普拉斯特征值计算过程的复杂度；通过找出不同时步网络的拉普拉斯特征值的递推关系公式，以网络初始状态为起点，可计算出所有不同增长模式下，GDURT网络的拉普拉斯特征值，其计算复杂度为关于网络规模Nt的多项式时间；根据递推关系可以发现GDURT网络的拉普拉斯特征值分布存在如下规律性：对于t时步的网络Ut，其特征值共有个（1+l）t，且特征值中不包含1，其中的（1+l）t-1个特征值与t-1时步的网络Ut-1的特征值完全相同，无需迭代计算。由某一时步的任意一个特征值均可递推计算出下一时步的1+l个特征值，且特征值的排序关系可以保持，所有的特征值都是互不相同的。

在此基础上进一步得出了GDURT网络的拉普拉斯特征向量的递推关系，准确找到了其特征向量分量与前一时步特征向量之间的关系，从而可以计算出所有不同增长模式下GDURT网络的拉普拉斯特征向量；并且发现了每一时步下，均存在任一特征向量的第一分量均恰好来自于前一时步对应的特征向量的特殊性质，利用这些性质可进一步缩减特征向量的计算时间。

［1］戴汝为.开展“系统复杂性”研究任重而道远［J］．复杂系统与复杂性科学，2004，1（3）：l-3．

［2］Borner K，Sanyal S，Vespignani A.Network science［J］.Annual Review of Information Science and Technology，2007，41：537-607.

［3］方锦清，汪小帆，郑志刚，等.一门崭新的交叉科学：网络科学（上）［J］.物理学进展，2007，27（3）：239-443.

［4］白勇，陆一南.复杂网络在传统经济系统上的模型研究［J］.计算机科学，2013，40（6）：265-267.

［5］Zhang Z Z，Zhou S G，Qi Y.Topologies and Laplacian spectra of a deterministic uniform recursive tree［J］.The European Physical Journal B，2008，63：507-513.

［6］Lu Z M，Guo S Z.A small-world network derived from the deterministic uniform recursive tree［J］.Physica A：Statis-tical Mechanics and Its Applications，2012，391，87-92.

［7］Lancaster P，Tismenetsky M.The Theory of Matrices with Applications［M］.Academic Press，New York，1985.

［8］章忠志.复杂网络的演化模型研究［D］.大连：大连理工大学，2006.

［9］Comellas F，Ozon J，Peters J G.Deterministic small-world communication networks［J］.Information Processing Letters，2000（76）：83-90.

Laplacian spectra of the generalized deterministic uniform recursive tree networks

ZHAO Hu
（The Computer College of Qinghai Normal University，Xining 810008，China）

The DURT（Deterministic Uniform Recursive Tree）networks model got a wide range of applications in the field of modeling and properties researching of complex networks.The GDURT（Generalized Deterministic Uniform Recursive Tree）evolution model is put forward on the basis of DURT network model.The complete recursive relations of Laplacian spectra （eigenvalues）and their corresponding eigenvectors are determined by the algebraic reduction and a special optimal layered method for nodes which can rapidly reflect the evolution characteristics of the networks.Some analysis is made to reveal the main characteristics of Laplacian spectra of GDURT networks.

complex networks；evolving model；uniform recursive tree；generalized；nodes layered；laplacian spectra

TP393.0

A

1674－6236（2016）03-0121-04

2015-06-17稿件编号：201506176

国家自然科学基金（61164005）。

赵 虎（1972—），男，青海西宁人，硕士，副教授。研究方向：复杂超网络模型构建与性质研究。