广义sinh-Gordon方程的新相互作用解

赵云梅

(红河学院数学学院，云南蒙自　661199)



广义sinh-Gordon方程的新相互作用解

赵云梅

(红河学院数学学院，云南蒙自661199)

利用两个Jacobi椭圆方程作为辅助方程，借助数学软件Maple，获得了广义sinh-Gordon方程的新相互作用解，这些解由反双曲正弦函数、Jacobi椭圆函数、双曲函数和三角函数组成.

广义sinh-Gordon方程;辅助方程;相互作用解;Jacobi椭圆函数

0　引言

2006年,Wazwaz[1]提出了广义sinh-Gordon方程

(1)

其中n是一个正整数，a,b是两个常数.sinh-Gordon方程的行波解被广泛应用于数学和物理等领域，由于它有着广泛的应用前景,所以许多作者已对它进行了大量研究，并获得了丰富的成果.Wazwaz[1]利用双曲正切函数方法得到了方程(1)的一些精确解.2008年,唐亚宁等[2]在三种函数变换的基础上研究了方程(1)的分支现象并得到了若干孤立波解、周期波解和Compacton解.2014年，何斌等[3]利用双F-展开法获得了方程(1)的若干双周期波解.

求解非线性偏微分方程的传统方法有F-展开法[4]、试探函数法[5]、Hirota双线性算子法[6]、Backlund变换法[7]、指数函数展开法[8]、辅助函数法[9]、Jacobi椭圆函数展开法[10]、双曲函数法[11]、(G/G)展开法[12],等等.这些方法都已成功地运用于多种非线性发展方程的求解过程中，并得到了一系列与它们相对应的孤立解、有理解、周期解、双周期解等多种类型的具有重要物理意义的精确解.

一直以来，人们在求解非线性发展方程时，常常得到的是单孤子解、双周期解或单周期解之间的多孤子解，却很少求得同时包含有理函数、三角函数、双曲函数或Jacobi椭圆函数的相互作用解，这些解可以反映不同类型非线性波之间的相互作用.

非线性偏微分方程的相互作用解最早是由马文秀教授提出的，文献[13]利用Wronskian行列式技巧和双线性形式求得了KdV方程的由三角函数与双曲函数相互作用(周期解与孤立波解之间)的相互作用解，Chen[14],Sun[15]和Meng[16]利用两个Jacobi椭圆方程作为辅助方程分别研究了(n+1)维sinh-Gordon方程、(2+1)维破裂孤子方程和(n+1)维sine-Gordon方程,获得了诸多几类函数之间的相互作用解.

本文利用两个Jacobi椭圆方程作为辅助方程，获得了方程(1)的许多新相互作用解.

1　广义sinh-Gordon方程的精确解

假设方程(1)的解可以表示成如下形式：

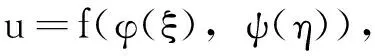
(2)

其中

则方程(1)可化为下列方程：

(3)

假设

(4)

这里φ(ξ),ψ(η)分别满足下列两个辅助方程:

(5)

(6)

其中P,Q,R是常数.把(4)式代入(3)式，并结合(5)和(6)式可知,(3)式的左边可化为一个关于φiψj的多项式，令此多项式的系数全为零，便得到一组关于A1,A2,A3,λ和c的代数方程组，利用Maple求解该代数方程组得到下列解：

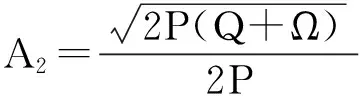
a=-c2,

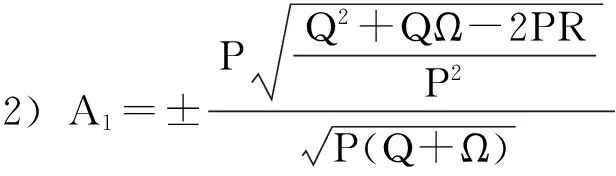
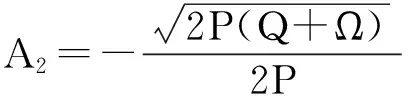
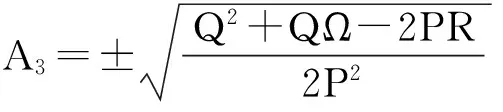
a=-c2,

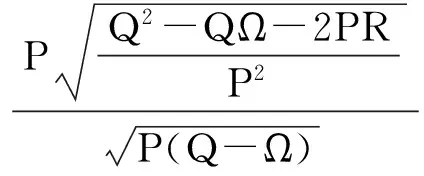
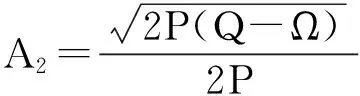
a=-c2,

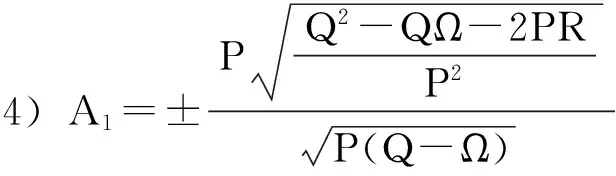
a=-c2,

把上述解代入(4)式,当P,Q,R取不同值时，就得到φ(ξ),ψ(η)的表达式,进而得到方程(1)用φ(ξ),ψ(η)表示的相互作用解.

下面列举P,Q,R的10种取值情形及获得的广义sinh-Gordon方程的相互作用解，其中ξ=λ(x+ct),η=λ(x-ct)，为了书写方便，记

情形1取P=1,Q=-(1+m2),R=m2，则φ(ξ)=sn(ξ,m),ψ(η)=sn(η,m)(或φ(ξ)=cd(ξ,m),ψ(η)=cd(η,m))，则方程(1)的相互作用解为

(7)

(8)

其中b=b1.当模m→1时，由(7)式可得

其中b=b4.

情形2取P=1-m2,Q=2m2-1,R=-m2，则φ(ξ)=cn(ξ,m),ψ(η)=cn(η,m)，于是方程(1)的相互作用解为

其中b=b2.

情形3取P=m2-1,Q=2-m2,R=-1，则φ(ξ)=dn(ξ,m),ψ(η)=dn(η,m)，于是方程(1)的相互作用解为

其中b=b3.

情形4取P=m2,Q=-(1+m2),R=1，则φ(ξ)=ns(ξ,m),ψ(η)=ns(η,m)(或φ(ξ)=dc(ξ,m),ψ(η)=dc(η,m))，于是方程(1)的相互作用解为

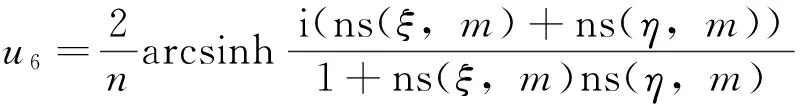
(9)

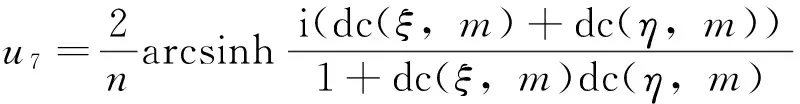
(10)

其中b=b1.当模m→1时，由(9)式可得

其中b=b4.当模m→0时，由(9)式可得

其中b=b5.当模m→0时，由(10)式可得

其中b=b5.

情形5取P=-m2,Q=2m2-1,R=1-m2，则φ(ξ)=nc(ξ,m),ψ(η)=nc(η,m)，于是方程(1)的相互作用解为

其中b=b2.当模m→0时，由(11)式可得

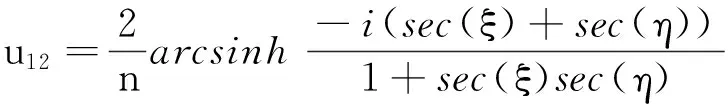
其中b=b5.当模m→1时，由(11)式可得

其中b=-b5.

情形6取P=-1,Q=2-m2,R=m2-1，则φ(ξ)=nd(ξ,m),ψ(η)=nd(η,m)，于是方程(1)的相互作用解为

其中b=b3.

情形7取P=1,Q=2-m2,R=1-m2，则φ(ξ)=sc(ξ,m),ψ(η)=sc(η,m),于是方程(1)的相互作用解为

(12)

其中b=b3.当模m→0时，由(12)式可得

其中b=-b4.当模m→1时，由(12)式可得

其中b=-b5.

情形8取P=1,Q=2m2-1,R=-m2(1-m2)，则φ(ξ)=sd(ξ,m),ψ(η)=sd(η,m)，于是方程(1)的相互作用解为

其中b=b2.

情形9取P=1-m2,Q=2-m2,R=1，则φ(ξ)=cs(ξ,m),ψ(η)=cs(η,m)，于是方程(1)的相互作用解为

其中b=b3.当模m→0时，由上式可得

其中b=-b4.

情形10取P=-m2(1-m2),Q=2m2-1,R=1，则φ(ξ)=ds(ξ,m),ψ(η)=ds(η,m)，于是方程(1)的相互作用解为

其中b=b2.当模m→0时，由上式可得

其中b=b5.

2　部分精确解的三维图形

下列图1～3是方程(1)部分精确解的三维图形.

n=4,λ=1,c=2,m=0.6 图1　u4的三维波形图Fig 13-D wave-form figure of solution u4

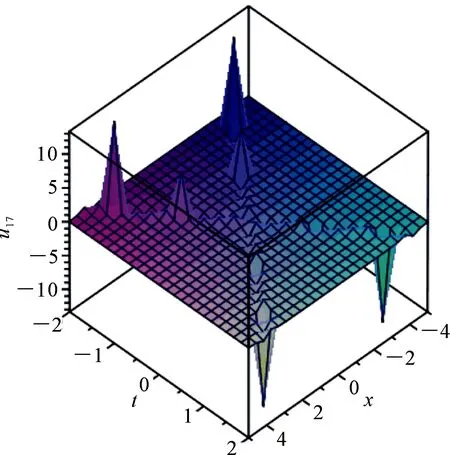
n=4,λ=4,c=2 图2　u17的三维波形图Fig 23-D wave-form figure of solution u17

n=4,λ=0.5,c=2,m=0.5 图3　u18的三维波形图Fig 33-D wave-form figure of solution u18

3　结束语

本文利用两个Jacobi椭圆函数作为辅助方程,研究了广义sinh-Gordon方程，获得了诸多包含反双曲正弦函数、Jacobi椭圆函数、双曲函数和三角函数的相互作用解，和文献[3]相比,本文所得到的相互作用解都为新解，更具普遍性.

[1]WAZWAZ A.Exact solutions for the generalized sine-Gordon and the generalized sinh-Gordon equations[J].ChaosSolitonsFractals,2006,28(1):127.

[2]TANG Yan-ning,XU Wei,SHEN Jian-wei,et al.Bifurcations of traveling wave solutions for a generalized sinh-Gordon equation[J].CommunNonlinearScienceNumericalSimulation,2008,13(6):1048.

[3]HE Bin,RUI Wei-Guo,LONG Yao.New exact double periodic wave and complex wave solutions for a generalized sinh-Gordon equation[J].ApplMatheComput,2014,229:159.

[4]傅海明，戴正德.耦合Klein-Gordon-Schrödinger方程的新精确解[J].西北师范大学学报(自然科学版)，2009，45(6):32.

[5]赵云梅.利用试探函数法求Drinfeld-Sokolov-Wilson方程组的精确解[J].西北师范大学学报(自然科学版)，2013，49(2):36.

[6]石玉仁，周志刚，张娟，等.(3+1)维ZK方程的孤立波解[J].西北师范大学学报(自然科学版)，2012，48(1):41.

[7]石玉仁，杨红娟，吕克璞，等.(3+1)维KP方程Backlund变换及其精确解[J].西北师范大学学报(自然科学版)，2006，42(4):34.

[8]赵云梅，芮伟国.用EXP-函数法求EqualWidth波方程的精确解[J].河南科技大学学报(自然科学版)，2008，29(2):94.

[9]套格图桑，斯仁道尔吉.新的辅助方程与非线性发展方程的孤立波解[J].内蒙古师范大学学报(自然科学汉文版)，2003，32(4):316.

[10]刘式适,傅遵涛,刘式达，等.Jacobi椭圆函数展开法及其在求解非线性波动方程中的应用[J].物理学报，2001,50(11):2068.

[11]石玉仁，段文山，吕克璞，等.变系数非线性Schrödinger方程的精确解[J].西北师范大学学报(自然科学版)，2004，40(2):27.

[12]刘文健,刘希强，桑波.非线性发展方程的新精确解[J].西北师范大学学报(自然科学版)，2012，48(2):31.

[13]MAWei-xiu.ComplexitonsolutionstotheKorteweg-deVriesequation[J].Phys LettA,2002,301:35.

[14]CHENHuai-tang,YINHui-chen.Doubleellipticequationmethodandnewexactsolutionsofthe(n+1)-dimensionalsinh-Gordonequation[J].J Math Phys,2007,48(1):013504-1-013504-7.

[15]SUNWei-kun,CAONan-bin，SHENYa-liang.Doubleellipticequationexpansionapproachandnovelsolutionsof(2+1)-dimensionalbreaksolitonequation[J].Commun Theor Phys,2008,49(2):281.

[16]MENGQing,HEBin,RUIWei-guo,etal.Newexactsolutionsofthe(n+1)-dimensionalsine-Gordonequationusingdoubleellipticequationmethod[J].Interna J Comput Math,2010,87(3):591.

(责任编辑马宇鸿)

New interaction solutions of the generalized sinh-Gordon equation

ZHAOYun-mei

(DepartmentofMathematics,HongheUniversity,Mengzi661199,Yunnan,China)

UsingtwoJacobiellipticequationsasauxiliaryequations,thegeneralizedsinh-Gordonequationisstudiedinthispaper.WiththeaidofmathematicalsoftwareMaple,manynewinteractionexactsolutionsofthegeneralizedsinh-Gordonequationareobtained.Thesesolutionsinvolvecombinationsofthearcsinhfunction,Jacobiellipticfunctions,hyperbolicfunctionsandtrigonometricfunctions.

generalizedsinh-Gordonequation;auxiliaryequation;interactionsolution;Jacobiellipticfunction

10.16783/j.cnki.nwnuz.2016.03.005

2015-06-06;修改稿收到日期:2015-09-18

国家自然科学基金资助项目(11161020,11361023)；云南省科技厅科研资助项目(2011FZ193,2013FZ117)；红河学院校级科研项目(XJ15SX07)

赵云梅(1972—)，女，云南泸西人，副教授，硕士.主要研究方向为偏微分方程.

E-mail:zhaoyunmei2000@126.com

O175.2

A

1001-988Ⅹ(2016)03-0018-04