NLOS环境下的高斯-粒子滤波无线跟踪技术

毛永毅, 燕琳凯

(1.西安邮电大学 电子工程学院， 陕西 西安 710121；　2.西安邮电大学 通信与信息工程学院， 陕西 西安 710121)



NLOS环境下的高斯-粒子滤波无线跟踪技术

毛永毅1, 燕琳凯2

(1.西安邮电大学 电子工程学院， 陕西 西安 710121；2.西安邮电大学 通信与信息工程学院， 陕西 西安 710121)

在非视距环境下，提出一种基于高斯变换的粒子滤波跟踪算法。该算法将高斯滤波和粒子滤波相结合，利用高斯滤波产生重要密度函数，考虑最新时刻的观测数据，使采样粒子更加接近于系统状态的后验概率分布。仿真结果表明，该算法在非视距环境下具有较高的估计精度，相比于粒子滤波算法，能够减少非视距误差的影响。

无线定位；非视距误差；粒子滤波；高斯变换；到达时间差

随着移动通信技术的快速发展，无线定位跟踪技术已经广泛应用在目标跟踪[1]、图像处理[2]和地图导航[3]等场合中。无线跟踪的方法主要包括基于信号强度(Signal Strength, SS)的方法、基于到达角度(Angle of Arrival, AOA)的方法和基于到达时间差(Time Difference of Arrival, TDOA)的方法等。其中，基于到达时间差的方法因简单实用且估计精度高，已成为最常使用的方法。文献[4-5]在TDOA算法的基础上提出了包括CHAN算法、Taylor序列展开法;文献[6]将CHAN算法和Taylor序列展开法进行了结合，提出了一种融合算法，但上述算法仅在视距(Line of Sight，LOS)环境下具有较高的精度。

在非视距(Non-line of Sight，NLOS)环境下，由于噪声的复杂和多径干扰，导致跟踪精度出现严重下降，故非视距误差是导致移动台估计精度下降的主要原因。文献[7]采用了一种基于无迹卡尔曼滤波的算法，该方法通过对非线性模型进行逼近来提高精度，但不适合非高斯环境中。文献[8]采用无迹粒子滤波对目标进行跟踪，在非线性非高斯环境下取得了一定的效果，但跟踪精度仍然有待提高。文献[9]提出一种高斯和的滤波新方法，该方法用高斯和的形式表示初始状态、系统噪声和观测噪声，但是仅适用于非高斯噪声的线性系统。

本文提出高斯粒子滤波跟踪算法，是在TDOA定位的基础上采用基于高斯变换的粒子滤波方法，在考虑最新观测值的同时，采用高斯分布近似系统后验概率分布，使采样粒子的分布更加接近系统状态分布。

1　粒子滤波跟踪算法

粒子滤波的基本思想是在状态空间中寻找一组随机样本(粒子)，来表示系统后验概率分布，以样本均值代替积分运算，从而获得最优贝叶斯估计[10]。蜂窝网无线跟踪系统属于非线性动态系统，将粒子滤波应用于TDOA定位方法中，利用3个基站的TDOA测量信息建立方程组。状态方程和测量方程可表示为

xk=f(xk-1)+ek-1=

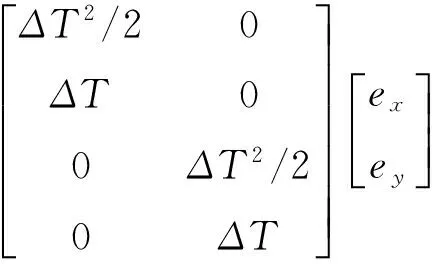
(1)

yk=h(xk)+nk=

(2)

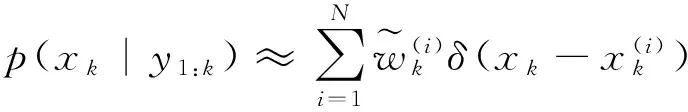
(3)

(4)

权值递推公式可表示为[11]

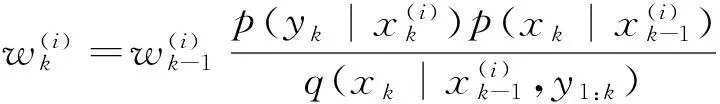
(5)

选择合适的重要密度函数是粒子滤波算法的关键步骤，最常用的方法是将先验密度函数作为重要密度函数进行采样[11-12]，即

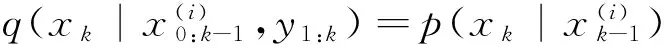
(6)

基于粒子滤波的跟踪算法步骤描述如下。

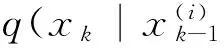
步骤3重采样：判断粒子退化情况，并进行重新采样。定义有效粒子数为[13-14]

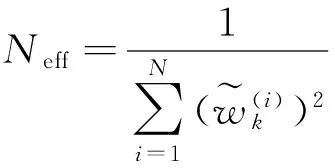
(7)

步骤4状态估计：k时刻的估计值

返回步骤2，计算下一时刻的状态值。

在粒子滤波无线跟踪算法中，将先验密度函数作为重要密度函数进行采样，没有考虑到最新的测量值，采样粒子的方差比从后验概率函数采样产生的方差大，滤波性能不理想，移动台跟踪误差也较大，故需要选择合适的重要密度函数来提高滤波精度。

2　高斯滤波

高斯积分公式[15]是一种高斯型积分公式，可以通过选取高斯点来提高代数精度，对任意一维函数g(x)，有积分公式

(8)

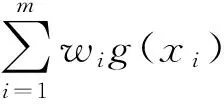
(9)

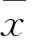
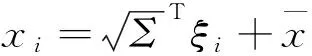
高斯滤波可以将系统状态的后验概率用高斯分布来近似，通过选取高斯点和相应的权值来提高滤波精度[17-18]。

假设k-1时刻系统状态及其方差分别为xk-1|k-1和Pk-1|k-1，由高斯点变换公式

和系统的状态转移方程得出系统状态及方差的一步预测分别为

xk|k-1][f(xi)-xk|k-1]Twi，

在已有的系统状态及其方差预测的基础上，由新的高斯点变换

与观测模型，系统状态及其方差的更新为

xk|k=xk|k-1+Kk(yk-yk|k-1),

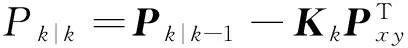
式中，Kk表示卡尔曼增益，yk|k-1表示观测值的预测，Pxy表示互相关协方差，Pyy表示预测的误差协方差，其中

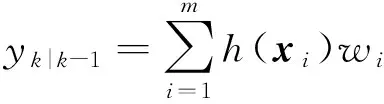
Kk=Pxy(R+Pyy)-1。

3　高斯-粒子滤波跟踪算法

将高斯滤波和粒子滤波结合并将其应用于蜂窝网无线跟踪中，以粒子滤波为基础，融合高斯滤波和最新的测量信息，从而使采样粒子的后验分布更接近系统实际的后验概率分布。高斯-粒子滤波无线跟踪算法的步骤如下。

利用式(5)计算粒子的重要性权值并进行归一化。

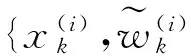
步骤5状态估计：k时刻的估计值

返回到步骤2，根据最新的观测值递归计算下一时刻的状态估计值。

4　仿真分析

将粒子滤波算法(PF)和高斯-粒子滤波算法(Gauss-PF)应用于TDOA蜂窝网跟踪中，并进行仿真分析。设置蜂窝网中基站的位置为

B1=(0,0)，B2=(0,200),

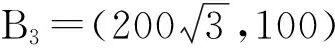
移动台初始位置为(10,10)，初始移动速度为(2,4)，过程噪声ek-1～N(0，1)，观测噪声nk～N(0,1)，测量时间间隔ΔT=1 s，粒子数N=100，采样时间为40 s，初始估计方差

P0=diag(2,0.5,2,0.5)，

新算法的高斯点数取m=3。对PF和Gauss-PF进行100次独立实验，两种算法的跟踪结果和误差对比分别如图1和图2所示。

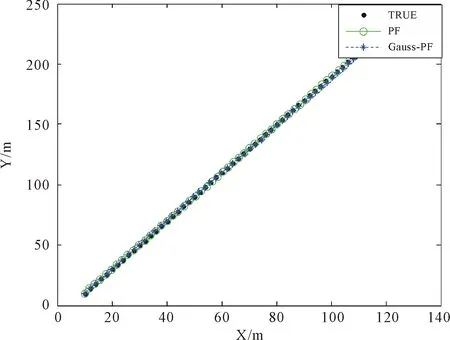
图1　两种算法的移动台跟踪效果

图2　两种算法的移动台跟踪误差对比

图1为基于PF算法和Gauss-PF算法的移动台跟踪结果。从图1中可以看出，PF和Gauss-PF均有比较好的跟踪效果，但是Gauss-PF的跟踪效果相比PF的跟踪效果相对精度更高一点，从跟踪轨迹可以看出，Gauss-PF的估计精度高于PF的估计精度。由于高斯粒子滤波跟踪算法减小了粒子退化现象，提高了滤波器性能，使高斯粒子滤波算法的跟踪精度高于粒子滤波算法。

图2为PF算法和Gauss-PF算法的移动台跟踪误差对比，从图2中可以看出，PF算法的均方根误差相对较大，Gauss-PF的均方根误差较小。由于Gauss-PF算法使用高斯滤波产生重要密度函数，考虑了最新时刻的观测数据，因此Gauss-PF算法能够减小误差。通过PF算法和Gauss-PF算法的对比，说明非视距环境中Gauss-PF算法的性能要优于PF算法。

5　结语

基于高斯-粒子滤波的无线跟踪算法，结合了高斯滤波和粒子滤波的优点，利用高精度的高斯积分公式得到较好的重要性密度函数，考虑了最新观测数据，采样后的粒子分布更加接近于系统状态的后验概率分布，在降低粒子退化的同时，提高了移动台估计精度。仿真结果表明，高斯-粒子滤波算法在非高斯噪声中有较好的估计精度，相比于粒子滤波算法，能够提高移动台估计精度，减少NLOS误差的影响。

[1]陈宝全,毛永毅.小波分析法解决无线定位跟踪问题[J/OL].电信科学, 2013, 29(10): 98-102[2015-12-25].http://d.wanfangdata.com.cn/Periodical/dxkx201310017.DOI:10.3969/j.issn.1000-0801.2013.10.017.

[2]ARAFA A, JIN X, BERGEN M H, et al. Characterization of image receivers for optical wireless location technology[J/OL]. IEEE Photonics Technology Letters, 2015, 27(18): 1923-1926[2015-12-25].http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=7150343.DOI:10.1109/LPT.2015.2446892.

[3]ZHOU J P, LIU L W, LIAO G F, et al. Predictive and fault-tolerant location service in mobile Ad Hoc networks[J]. Wireless Personal Communication, 2013, 71(4): 3115-3130.

[4]ZHANG J W, YU C L, JI Y Y. The performance analysis of Chan location algorithm in cellular network[J/OL]. Computer Science and Information Engineering, 2009, 416: 339-343[2015-12-25].http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=5171188.DOI:10.1109/CSIE.2009. 416.

[5]周康磊, 毛永毅. 基于残差加权的Taylor级数展开TDOA无线定位算法[J/OL]. 西安邮电大学学报, 2010, 15(3):10-13[2015-12-25]. http://d.wanfangdata.com.cn/Periodical/xaydxyxb201003003.DOI:10.3969/j.issn.1007-3264.2010.03.003.

[6]刘林,邓平,范平志.基于Chan氏算法和Taylor级数展开法的协同定位方法[J/OL].电子与信息学报,2004,26(1):41-46[2015-12-25]. http://jeit.ie.ac.cn/CN/Y2004/V26/I1/41.

[7]ZUO J Y, JIA Y N, GAO Q X. Simplified unscented particle filter for nonlinear/ non-Gaussian Bayesian estimation[J/OL]. Systems Engineering and Electronics. 2013, 24(3):537-544[2015-12-25].http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=6550965.DOI:10.1109/ JSEE.2013.00062.

[8]PEI F, WU M, ZHANG S. Advanced distributed unscented particle filter for simultaneous localization and mapping[J]. Future Computer & Information Technology, 2013, 11(12):953-962.

[9]林青,尹建君,张建秋,等. 非线性非高斯模型的高斯和滤波算法[J/OL]. 系统工程与电子技术, 2010,32(12):2493-2499[2015-12-25].http://www.sys-ele.com/CN/10.3969/j.issn.1001-506X.2010.12.01.

[10] 王法胜, 鲁明羽, 赵清杰,等. 粒子滤波算法[J/OL]. 计算机学报, 2014, 37(8):1679-1694[2015-12-25].http://cjc.ict.ac.cn/qwjs/view.asp?id=4318. DOI: 10.3724/SP.J.1016.2014.01679.

[11] FA S W, YUE J L. Improving particle filter with a new sampling strategy[J/OL]. Computer Science & Technology, 2009, 140(2): 107-113[2015-12-25].http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=5228418.DOI:10.1109/ICCSE.2009.5228418.

[12] SAIKAT S, FREDRIK G. Particle filtering with dependent noise processes [J/OL]. IEEE Trans on Signal Processing. 2012, 60(9):4479-4508[2015-12-25].http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=6212404.DOI:10.1109/TSP.2012.2202653.

[13] 左军毅,张怡哲,梁彦. 自适应不完全重采样粒子滤波器[J/OL]．自动化学报，2012, 38(4): 647-652[2015-12-25].http://d.wanfangdata.com.cn/Periodical/zdhxb201204017.DOI:10.3724/SP.J.1004.2012.00647.

[14] GONZALES C, DUBUISSON S. Combinatorial resampling particle filter: an effective and efficient method for articulated object tracking[J/OL]. International Journal of Computer Vision, 2014, 112(3): 255-284[2015-12-25].http://link.springer.com/article/10.1007%2Fs11263-014-0763-z.DOI:10.1007/s11263-014-0763-z.

[15] KAZUFUMI I, XIONG K Q. Gaussian filter for nonlinear filtering problems [J/OL]. IEEE Trans on Automatic Control. 2000, 45(5):910-927[2015-12-25].http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=912021.DOI:10.1109/CDC.2000.912021.

[16] 袁泽剑,郑南宁,贾新春. 高斯-厄米特粒子滤波器[J/OL]. 电子学报， 2003, 31(7): 970-973[2015-12-25].http://www.ejournal.org.cn/CN/Y2003/V31/I7/970.DOI:10.3321/j.issn:0372-2112.2003.07.003.

[17] JAECHAN L, DAEHYOUNG H. Gaussian particle filtering approach for carrier frequency offset estimation in OFDM systems[J/OL]. IEEE Signal Processing Letters, 2013, 20(4): 367-370[2015-12-25].http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=6468071.DOI:10.1109/LSP.2013.2248148.

[18] YANG J L, JI H B, LIU J M. Gauss-Hermite particle PHD filter for bearings-only multi-target tracking[J/OL]. Systems Engineering & Electronics, 2013, 35(3): 457-462[2015-12-25].http://www.sys-ele.com/EN/10.3969/j.issn.1001-506X.2013.03.01.

[责任编辑:祝剑]

Wireless location technology of Gauss particle filter under NLOS environment

MAO Yongyi1，YAN Linkai2

(1. School of Electronic Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China；2.School of Communication and Information Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

In nonlinear non-Gaussian environment, a novel particle filter localization algorithm based on the Gauss transform is proposed. The novel algorithm combines Gaussian filtering with particle filter, and the important density function is obtained by Gaussian filtering. The algorithm also takes into account the latest observations, and therefore the particle distribution is closer to posterior probability density function of the system state. Simulation results show that the novel algorithm has higher location accuracy in non-line of sight environment. Compared with the classical particle filter algorithm, the novel algorithm can reduce the NLOS error.

wireless location, non line of sight, particle filter, Gauss transform, time difference of arrive

10.13682/j.issn.2095-6533.2016.04.002

2015-12-25

陕西省自然科学基金资助项目(2014JM2-6088)

毛永毅(1969-)，男，教授，博士，从事导航与定位方向研究。E-mail：maoyongyi@263.net

燕琳凯(1989-)，男，硕士研究生，研究方向为宽带无线通信。E-mail：694062184@qq.com

TP393

A

2095-6533(2016)04-0009-05