中砂动力学参数的共振柱试验研究

曹文冉，许　浩，罗小桥，张月超1.中国石油集团工程技术研究院，天津 3004512.中国石油天然气集团公司海洋工程重点实验室，天津 300451

中砂动力学参数的共振柱试验研究

曹文冉1，2，许浩1，2，罗小桥1，2，张月超1，2
1.中国石油集团工程技术研究院，天津 300451
2.中国石油天然气集团公司海洋工程重点实验室，天津 300451

海底管道建设必须考虑地震的影响。动剪切模量和阻尼比是表征土体在地震作用下力学性能的重要指标，对海底管道的抗震设计和安全评价均有不可忽视的影响。以国内某海底管道工程为依托，以中砂为研究对象，采用NGZ型自由振动式共振柱试验系统，探讨了共振柱试验基本原理和土动力学参数计算方法，研究了不同围压下动剪切模量和阻尼比随剪应变的变化规律。试验结果表明：随着剪应变的增大，中砂的动剪切模量逐渐减小，阻尼比则逐渐增大，具有非线性与滞后性的变化规律。

中砂；动力学参数；共振柱；围压

随着海洋油气资源的不断开发，海底管道在我国得到了广泛应用，发挥着越来越重要的作用。由于我国是一个多地震国家，蕴藏丰富油气资源的渤海、黄海、东海又濒临环太平洋地震带［1］，因此海底管道建设必须考虑地震的影响。在海底管道抗震分析中，动剪切模量和阻尼比是表征土体在地震作用下力学性能的重要指标，前者用于反映土体动剪应力与动剪应变之间的关系，后者用于反映土体应力-应变关系的滞后性［2］。这两个参数取值合理与否对海底管道的抗震设计和安全评价均有不可忽视的影响。

共振柱试验是通过改变振动频率使圆柱形试样产生共振并借以测求试样的动剪切模量、阻尼比等参数的试验［3］。这种方法始于20世纪30年代，首先由日本学者阪田在砂性土动力特性研究中应用；20世纪60年代后，经过Wilson等学者的努力，共振柱试验才取得较大范围的应用和发展［4］。近十多年来，国内外学者利用共振柱对砂性土动力学参数开展了大量的试验研究［5-7］，得到了很多有价值的结论，主要集中于小应变幅值条件下动剪切模量和阻尼比变化规律的研究。

本文以国内某海底管道工程为依托，以中砂为研究对象，采用NGZ型自由振动式共振柱试验系统，探讨共振柱试验基本原理和土动力学参数计算方法，通过给定不同的围压，研究动剪切模量和阻尼比随剪应变的变化规律，为地震作用下海底管道的动力反应分析和地震模拟振动台试验提供参数依据。

1　共振柱试验基本原理［3-4］

共振柱试验是在一定湿度、密度和应力条件下的圆柱形土样（空心或实心）上施加纵向振动或扭转振动，并逐级改变驱动频率，测出土样的共振频率，再切断动力，记录振动衰减曲线，然后根据这个共振频率以及试样的几何尺寸和端部限制条件，计算出试样的动弹性模量Ed或动剪切模量Gd，根据衰减曲线计算出阻尼比λ。

在共振柱试验中，试样的端部限制条件是个关键性的问题，通常以底端固定、顶端自由较为适宜。但由于共振柱试验必须既激振试样又测量振动运动，因此试样上部必须安装驱动装置和测量仪器，从而使试样顶端的边界条件发生改变。设试样的高度为L，底端固定，顶端附加一个集中质量块m，并通过该质量块对试样施加垂直轴向或水平扭转振动，这样共振柱试验可简化成如图1所示的模型。

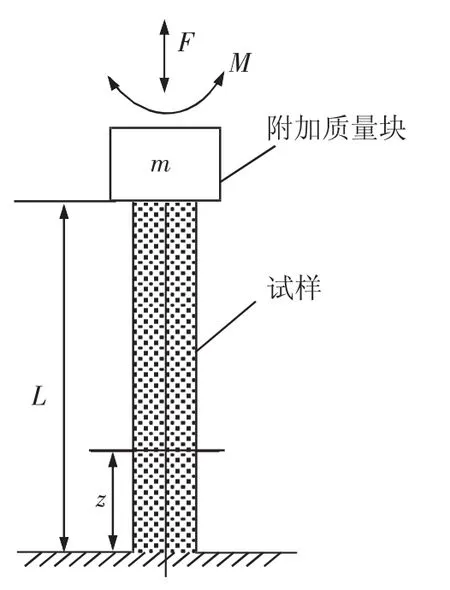
图1　共振柱试验模型

当试样的顶端受到驱动器所施加的周期荷载而处于强迫振动时，这种振动将由柱体顶端以波动形式沿柱体向下传播，使整个柱体处于振动状态。把试样视为弹性体，忽略试样横向尺寸的影响，那么振动所引起的位移（u或θ）将是位置坐标z和时间t的函数。以扭转振动为例，引入一维波动方程，可得：

式中：cs为剪切波速，G为试样的剪切模量，Pa；ρ为试样的密度，kg/m3。

上式的解可写为：

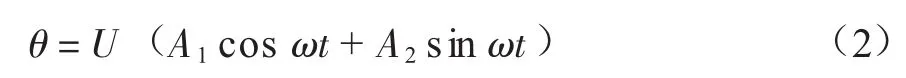
式中：U为位移幅值，m；ω为试样的固有频率，Hz；A1、A2为常数。

将式（2）代入式（1）并解之，得：

式中：A3、A4为常数。

考虑试样的边界条件，当z=0时，U=0；当z =L时，根据胡克定律有：

式中：I为试样的惯性矩，m4；Jm为附加质量块的极惯性矩，m4。

上式为扭转振动时的频率方程，可见只要有试样与附加质量块的极惯性矩的任意比值就可得到βs，进而得到：

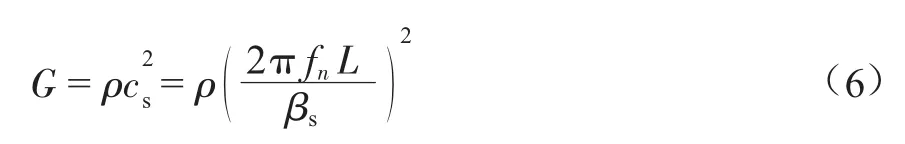
式中：fn为通过共振柱试验测得的试样振动固有频率，Hz。

阻尼比可通过自由振动法测得，即当试样发生共振时切断动力，使试样在无干扰力的条件下自由振动，测定其衰减曲线并给出振动次数和相对振幅之间的关系曲线，再按下式计算：

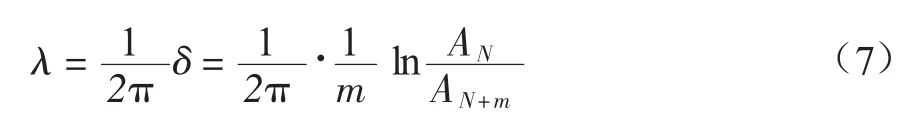
式中：δ为对数衰减率；AN为第N次的振幅，m；AN+m为第N+m次的振幅，m。

在实际应用中，由于试样激振端压板系统的质量影响，利用上述公式处理数据较为复杂。当激振端具有弹簧-阻尼器时，试验数据的处理通过专用的计算机程序才能完成。

2　重塑中砂共振柱试验

2.1试验仪器

试验仪器采用NGZ型共振柱试验机，主要由三轴压力室、扭轴激振组件、控制系统、采集系统等组成，如图2所示。

图2　NGZ型共振柱试验机

这是一台完全由计算机控制，集控制、采集、分析和显示于一体的土动力试验测试设备，可在试样未破损的小应变范围内（10-6～10-4）用自由振动法确定土的动剪切模量和阻尼比。

共振柱试验机的主要技术指标如下：加振方式为电磁力激发自由振动，最大均等静压力为450 kPa，最大扭矩为100 N·cm，频率范围为0～100 Hz，试样尺寸有φ39.1 mm×80 mm、φ50 mm×80 mm两种，剪应变范围为5×10-6～5×10-4。

2.2试验土样

由于客观原因，本文难以直接获取所述海底管道工程的场地砂样。考虑到振动台试验主要对模型管道进行定性研究，因此试验土样取自黑龙江省哈尔滨市松花江江心岛周边，为非饱和、欠固结土。为了解土样的工程特性，在共振柱试样制备前进行了含水率、土粒相对密度、密度、颗粒分析、干密度等物理性质试验。试验结果见表1和表2。

表1　基本物理指标

表2　　颗粒分析试验结果

从表2可以看出，试验土样粒径≤0.075 mm的细粒质量分数为5.41%，在5%～15%之间，属于含细粒土砂；粒径大于0.25 mm的颗粒质量超过了总质量的50%，可判定为中砂。

根据标准［8-9］要求制备试验砂样，步骤如下：

（1）称取试验要求的砂样质量，分成3份，煮沸后冷却备用。

（2）在压力室底座上依次放透水板、橡皮膜和对开圆模，将橡皮膜从对开模两端翻出，通过抽气的方法使两者紧贴。

（3）在橡皮膜内注入纯水至试样高度的1/3，将每份砂样填入膜内，填至该层要求的高度，依次第二层、第三层，直至膜内填满为止。

（4）整平砂面，放上透水板和试样帽，扎紧橡皮膜。

（5）对试样内部施加负压力使试样站立，拆除对开圆模。

（6）用游标卡尺分别测量试样3个不同位置的直径和高度，取其平均值，以保证试样形状为直径39.1 mm、高度80 mm的实心圆柱体，如图3所示。同时复核试样干密度，以确保各试样的干密度差值小于0.03 g/cm3。

图3　实心圆柱体试样

2.3试验方法

待试样安装完毕后，按照图4所示的试验流程开展重塑砂样的共振柱试验。

图4　试验流程

测试时，首先使试样在静力作用下固结稳定，然后再在不排水条件下施加扭转振动。同时监控饱和试样在围压下的孔隙水压力系数，确保其不小于0.98。

试验围压分别取100、150、200 kPa。试验过程如下：首先对试样施加瞬时扭矩后立即卸除，使试样自由振动；然后在上一级应变幅值的激振试验结束后，继续增大激振力，得到试样在下一级应变幅值下的剪切模量和阻尼比，直至应变幅值增大到10-2为止；最后增大试样的侧向压力和轴向压力，排水固结后重新进行试验。

3　试验结果及分析

3.1动力变形特性

为了降低仪器精度误差，同时考察本试验的可重复操作性，在相同试验条件下反复试验3次，采用重复试验的平均值来分析模量比（G/Gmax）与阻尼比（λ）随剪应变的变化关系，见表3。

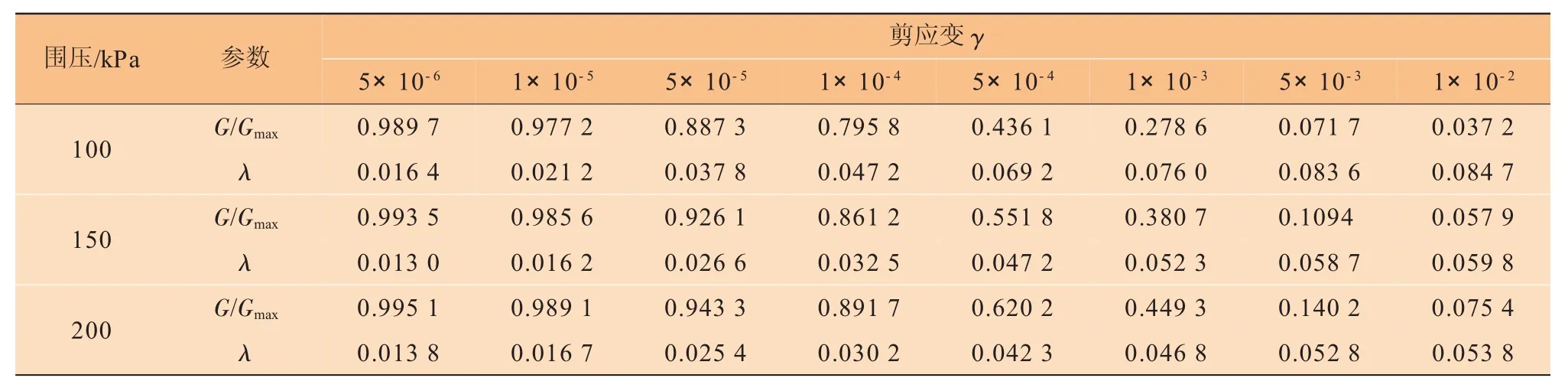
表3　　不同围压条件下动力学参数试验结果

一般情况下，当应变小于10-4时，采用共振柱仪来测定砂土的动力参数，当应变大于10-4时，需要改用振动三轴仪。在文献［7］中，张亚军等采用修正过的模型拟合了应变大于10-4时的共振柱试验数据，并与振动三轴试验结果进行了比较，结果发现G/Gmax-γ和λ-γ曲线拟合较好。由于本文中剪应变达到了10-2，因此直接采用共振柱试验结果来研究中砂的动力特性。各组试样的动力变形特性曲线见图5。

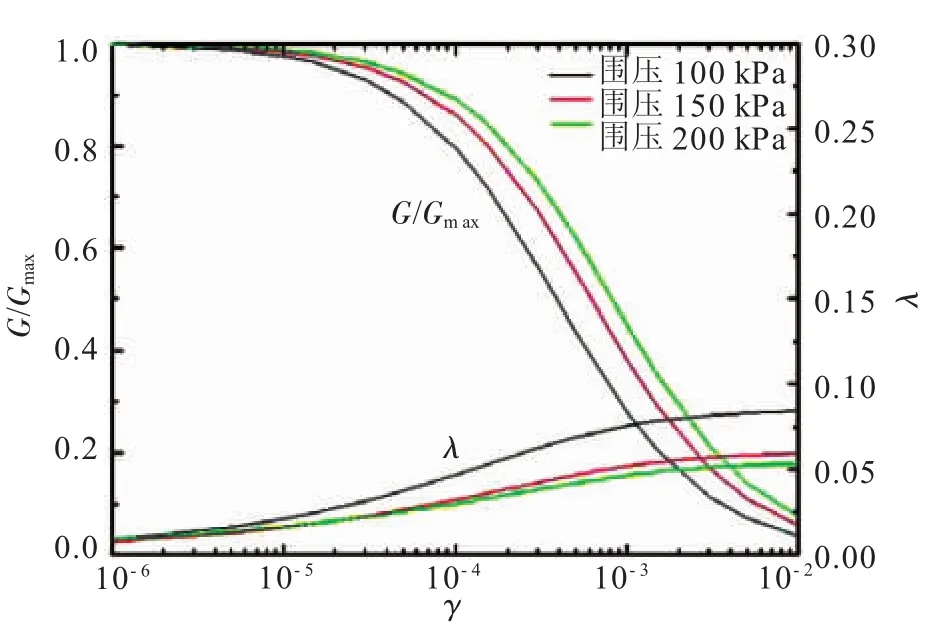
图5　　不同围压下模量比和阻尼比随剪应变的变化

3.2动剪切模量

从图5可知，在扭转激振条件下，不论围压的大小如何，动剪切模量G都随剪应变γ的逐渐增大而衰减。当γ在10-6～10-4时，G变化缓慢；当γ大于10-4时，G衰减梯度迅速变大，至γ=10-2时减至最大动剪切模量Gmax的10%左右。由此判断，当剪应变在10-5～10-4时，试样已经进入弹塑性，土体的非线性、滞后性和不可恢复变形都开始显现。随着剪应变的进一步增加，试样的动剪切模量变化越来越明显，逐渐接近了极限值，此时土体已进入塑性破坏状态。因此，中砂的动剪切模量随剪应变的变化具有非线性与滞后性。

图6给出了动剪切模量归一化曲线线性拟合及系数a、b的取值。

图6　　动剪切模量归一化曲线线性拟合

从图5和图6均可以看出，在同一剪应变幅值下，围压越大，动剪切模量越大。分析其原因在于，围压增大，试样的孔隙比就会减小，颗粒之间的接触点随之增多，那么应力波在土体中的传播就会更快，从而导致了动剪切模量变大。但是，如果剪应变持续增大，那么围压和孔隙比对土体动力参数的影响则会逐渐减弱。

3.3阻尼比

一般情况下，土体振动时存在逸散阻尼和材料阻尼，前者由波的扩散引起，后者由土体特性引起［7］。本文分析以材料阻尼为主。

从图5可以看出，试样的阻尼比比较小，在小剪应变幅值（γ＜10-4）时变化不明显，但是随着剪应变的增大，阻尼比的非线性快速增加。在同一剪应变幅值下，围压越大，阻尼比越小。但是，当围压进一步增大时，阻尼比渐渐趋于一致。

4　结论

本文采用NGZ型自由振动式共振柱试验系统研究了不同围压下中砂动剪切模量和阻尼比随剪应变的变化规律。通过分析共振柱试验成果，得到了如下主要结论：

（1）不论围压大小如何，中砂的动剪切模量都随着剪应变的增大而衰减，阻尼比都随着剪应变的增大而增大。在小剪应变（＜10-4）条件下，两者的变化比较缓慢；随着剪应变的增大，动剪切模量的衰减梯度迅速变大，阻尼比非线性迅速增加。

（2）在相同剪应变条件下，随着围压增大，中砂的动剪切模量提高，阻尼比降低。当剪应变足够大（接近10-2）时，动剪切模量接近最大动剪切模量的10%，阻尼比开始趋于稳定。此时，通过提高围压来影响动剪切模量和阻尼比变得不再明显。

（3） 当剪应变在10-5～10-4时，中砂处于弹塑性阶段，但不可恢复变形开始显现。随着剪应变的进一步增加，中砂快速进入了塑性破坏状态。

由此可见，中砂动力学参数随剪应变的变化具有非线性与滞后性，为所述海底管道工程的地震响应分析提供了参数依据。

［1］许东禹，刘锡清.中国近海地质［M］.北京：地震出版社，1997.

［2］李剑，陈善雄，姜领发，等.重塑红黏土动剪切模量与阻尼比的共振柱试验［J］.四川大学学报（工程科学版），2013，45（4）：62-68.

［3］吴世明.土动力学［M］.北京：中国建筑工业出版社，2000.

［4］张克绪.土动力学［M］.北京：地震出版社，1989.

［5］王炳辉，陈志强，张婷.南京细砂动剪切模量和阻尼比的试验研究［J］.世界地震工程，2010，26（3）：8-15.

［6］ESTELLE D，IRINI D M，RICHARD C，et al.Shear Modulus and Damping Ratio of Grouted Sand［J］.Soil Dynamics and Earthquake Engineering，2004，（24）：461-471.

［7］张亚军，兰宏亮，崔永高.上海地区土动剪切模量比和阻尼比的统计研究［J］.世界地震工程，2010，26（3）：171-175.

［8］GB/T50269-97，地基动力特性测试规范［S］.

［9］SL237-1999，土工试验规程［S］.

中国石油天然气集团公司科学研究与技术开发项目（BK-14 -05-H2）。

Resonant Column Test on Dynamic Parameters ofMedium Sand

CAO Wenran1，2，XU Hao1，2，LUO Xiaoqiao1，2，ZHANG Yuechao1，2
1.CNPC Research Institute of Engineering Technology，Tianjin 300451，China
2.CNPC Key Laboratory of Offshore Engineering，Tianjin 300451，China

The seismic action shall be taken into account in the construction of submarine pipeline.Dynamic shear modulus and damping ratio are important parameters to characterize the soilmechanicalproperties during earthquake，which have a significant influence on aseismic design and safety elevation of submarine pipeline.Using the medium sand as the research object on the basis of a submarine pipeline project in China，the basic principle of resonant column test as well as the calculation method of soil dynamic parameters are discussed and the variation of dynamic shear modulus and damping ratio with shear strain under different confining pressures is studied by using the free vibration column test system named NGZ Type.The test results show that the dynamic shear modulus of the medium sand decreases and the damping ratio increases with the increase of shear strain，which presents the law of nonlinear and hysteresis.

medium sand；dynamic parameter；resonant column；confining pressure

10.3969/j.issn.1001-2206.2016.01.007

曹文冉（1984-），男，山东滨州人，工程师，2009年毕业于哈尔滨工业大学防灾减灾及防护工程专业，硕士，现从事海洋平台和海底管道研究工作。Email：caowenran@cnpc.com.cn

2015-04-10；

2015-11-08