题后反思是学好数学的助力剂

☉江苏省东台中学 周冬波

题后反思是学好数学的助力剂

☉江苏省东台中学 周冬波

波利亚在《怎样解题》中将解题分为四步——理解题目，拟定计划，执行计划和回顾.由此可看出，解题后的反思是解题的重要组成部分.通过回顾完整的答案，重新审查解答，可巩固知识，培养解题能力.波利亚认为“没有任何一个题目是彻底完成的，总还会有事情可做，在充分的研究和洞察后，我们可以将任何解法加以改进，无论如何，总可以深化我们对答案的理解”.解题后反思可以将不同的问题相互联系，不同知识相互联系，也可以将已获得的解题方法或结果利用到其他问题的求解.养成反思的习惯可获得一些条理分明，随时可用的知识，将会提高你的解题能力.

一、引导学生对解题过程进行反思

引导学生对解题过程进行反思，看看有没有思维回路，以培养思维的合理性、条理性、敏捷性.反思解题过程是否合理，公式的运用是否考虑公式的适用范围，可提高我们思维的完整性；反思解题思路是否严谨，有无逻辑漏洞，可提高我们思维的严谨性；反思解题方法能否优化，能不能“一题多解”，能否从不同角度思考同一问题，这样不但增加知识间的联系，将知识系统化、知识网，还能锻炼我们思维的灵活性.对解题规律进行反思的目的在于能够让学生更加清楚地理解知识、掌握知识，在反思中进行自我完善，提高解题能力.

例1 求过点P（3，2），并且与两坐标轴的正半轴所围成的三角形的面积最小时直线l的方程.

ab≥24，故S△AOB=，当且仅当时等号成立，此时a=6，b=4.

解法二（点斜式法）：设所求直线l的方程为y-2=k（x-3）（k＜0），它与两坐标轴的正半轴的交点为AB（0，2-3k），则

解法三（面积分割法）：如图1，作PM，PN分别垂直x轴、y轴于M、N.设直线l与x轴，y轴的交点分别为A，B，且|AM|=m，|BN|= n，则S=6.又△BNP∽△PMA，所以可得，即mn=6.

图1

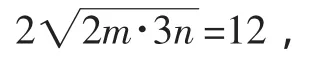
当且仅当2m=3n时，S△AOB=12，此时A（6，0），B（0，4），因此所求直线l的方程为，即2x+3y-12=0.

解决此类题型的通性通法是用截距式和点斜式，但解法三（面积分割法）不落俗套，将△AOB的面积分割为矩形面积（定值）和两个三角形面积之和，从变中觅不变，解法比较巧妙.

二、引导学生对解题规律进行反思

高中数学复习中的学生每天都耗在题海中，题做了不少，但收效甚微，究其原因，最重要的是缺乏对解题规律的反思、总结，难于形成一般性的结论.解题的基本目的使学生更加牢固掌握所学的知识，并能够灵活的应用，同时形成一定的解题的技能，实现思维的迁移.因此，教师在解题后应注重引导学生对问题的实质剖析、反思：所求问题转化成什么数学问题？涉及哪些知识？它们之间是否存在某种联系和规律，解题的技巧是什么？能否总结成一般性的结论？如果能够持之以恒，久而久之，便能做到举一反三、逐类旁通、事半功倍的效果.

例2 设集合I=｛1，2，3，4，5｝，选择I的两个非空子集A和B，要使B中的最小数大于A中的最大数，则不同的选择方法共_______种.

简解：学生分A为｛1｝，B为｛2，3，4，5｝；A为｛2｝，则B为｛3，4，5｝；A为｛3｝，则B为｛4，5｝……等等八种情况列举，再逐个算出来再求和，共49个选择方法.

那本题能否进行更一般的推广？引导学生推广到更一般的问题：

设集合I=｛1，2，3，...，n｝，选择I的两个非空子集A和B，要使B中的最小数大于A中的最大数，则不同的选择方法共_______种.

解：（1）A中最大元素为1，这样的A共1个，对应的B 有2n-1-1个，这样的（A，B）对2n-1-1个；

（2）A中最大元素为2，这样的A共21个，对应的B有（2n-2-1）个，这样的（A，B）对21（2n-2-1）个；

（3）A中最大元素为3，这样的A共22个，对应的B有（2n-3-1）个，这样的（A，B）对22（2n-3-1）个；

（n-1）A中最大元素为n-1，这样的A共2n-2个，对应的B有（21-1）个，这样的（A，B）对2n-2（21-1）个.

共计（n-2）2n-1+1种选择方法.

此题就是先优化解题过程，从特殊到一般，从简单的问题挖掘出更一般的方法，再用之解决一般性问题.当然不同的问题，反思的角度不是固定的.通过这种反思使学生认识到类比思想，特殊到一般的思想是数学中重要解题方法，起到做一题，得一法，明一类的效果，更重要的是促进学生思维能力的迁移.

三、引导学生在解题的错误处反思

解数学题，出现错误在所难免，出现错误的因素多种多样，有的因为审题不清，有的因为概念模糊，有的因为解题策略有误，有的因为运算量大、计算马虎等，解题出现错误并不可怕，关键是要重视错误，反思错误，找出错误的地方，是由于什么原因导致的，如何改正，给学生一个对基础知识重新理解的机会，使学生在纠错的过程牢牢掌握基础知识，在反思中不断得到提高.

例3 已知圆的方程x2+y2+2x+ky+k2=0和某一定点P（1，1），要使过点P所作圆的切线有两条，求k的取值范围.

因为过P点要作圆的两条切线，

所以P点在圆外，

反思本例的解题错误，是由于对圆的一般方程这一概念不够清楚，因为方程x2+y2+Dx+Ey+F=0表示的曲线不一定是圆，也可能是一个点或没有图形，只有化成标准形式：，且D2+E2-4F＞ 0时，此方程才表示圆，

此题正是由于忽视这个条件出错，因此，必须同时

通过对此错解题的反思，可以帮助我们及时发现解题过程出现的错误，剖析错误的原因，并及时地加以纠正，这样，既加深对基本概念的理解，又为以后正确、灵活应用奠定坚实的基础，更重要的是通过这种反思可极大培养学生思维的批判性.

四、引导学生对题中的知识点进行反思

解一道数学题，所涉及到的知识往往不止一个，而是需要众多知识点加以综合解决，这就要求我们的思维以一定的顺序有机的把这些知识结合起来，按照数学的符号、逻辑，有条理地写出解题过程.然而我们头脑中的数学基础知识如概念、定理、公理是比较零乱形式存在，并没有建立起有效的实质的联系，这种较低水平的认知，往往会妨碍我们对问题的解决，导致所学的知识不能有效的发挥，此时，如果教师能够在解题后引导学生对所涉的知识点及它们之间的联系进行反思，不但可以加深对数学知识的理解，更重要的是强化了各知识点间紧密性，为以后灵活、综合地应用所学知识奠定了坚实的基础.

例4 判断直线l：ax+by+b-a=0与⊙C：x2+y2-x-2=0的位置关系.

反思：本题的几何对象是：直线l及⊙C；几何特征：动直线、定圆、判断两者位置关系.

策略1：代数化：直线与⊙C方程联立的方程组有两组解，转化成一元二次方程根的判别式问题.

策略2：代数化：转化成圆心到直线的距离与半径比较大小，圆心到直线的距离有点到直线的距离公式可以代数化.

策略3：深入揭示几何对象的特征：由动直线l：ax+by+b-a=0的方程进一步揭示直线l过定点（1，-1）.由圆的方程可以发现其几何特征为圆心为，半径为将点（1，-1）横纵坐标代入圆的方程左边，计算其结果小于0，从而可以判断直线所过定点在圆内，即可得到直线与圆相交.

反思题目所涉及的知识点，比较获取思路的方法及其各种方法优劣：策略1、2思路获取简单，但是运算复杂且技巧性较大，运算费时且不易从中走出，而深入地揭示几何对象的几何特征明显简便的多.解题不单单是一种知识的体现，它是学生对所学知识的一种综合检验，如果学生不能对所涉及的知识进行反思，就不能得出新的知识.

总之，解出一道数学题并不是解题思路的结束，而是更深入探究的开始，为发挥一道题的功效，教师必须从不同的角度，不同的侧面去启发学生思考和探索解决问题的策略方法.在日常的教学中，我们要强化学生在解题后反思的意识，要指导学生进行有方向的反思，要让学生有反思的经历.只有这样，学生才能跳出“题海”，才能“以一题挡百题”，才能将知识巩固，能力提高，思维深化.如果解题后不进行反思，很容易因为忽视某些因素导致解题的不完整或错误，因此，我们必须从平时的每一节课、每道习题开始养成解题后反思的习惯，及时发现遗漏，弥补遗漏，完善过程，最大限度减少错误，避免错误，从而更深刻、更准确、更全面对概念、定理、公理进行理解，这对培养学生思维的深刻性也大有裨益.