一道阶段考试题解法探究及教学反思

☉河北省任丘市第一中学 邓满囤

一道阶段考试题解法探究及教学反思

☉河北省任丘市第一中学 邓满囤

前期本校阶段考试的最后一道选择题，答对率很低，引起了笔者的深入思考.学生在数学解题活动中，或者一头雾水没有思路，或者思路受阻时不知如何调整到正确的轨道上来.关键是学生对题目信息不知如何整合与转换，教师在解题教学中，如何引导学生“思维辨析”，由点及面，由面及体的良性循环.下面就本校一道考试题为例，简要分析，与各位同仁分享.

一、题目展示

二、思维视角

视角1：估算思想，特殊化方法

估算是以正确的算理和对所研究的问题的特征已深刻理解为前提，通过大致估值、合理猜测或特值引路等手段，进行粗略、近似的计算而得到正确结果的解题手段.在数学解题中渗透估算意识，能有效地避开以往“小题大作、费时费力”的逻辑推理过程，达到了简捷、快速、合理、准确的解题目的，恰到好处地符合了近年高考命题提倡的“多考一点想，少考一点算”的精神.更确切地说，估算是一种数学思维方法，也是一种求简策略.

高考数学选择题主要考查学生对基本知识的理解程度、基本技能的掌握情况、基本运算的合理性.学生考虑问题要全面、迅速获得问题结论，注重在知识网络的交汇点处设计问题，体现各种数学思想和方法.所以，求解选择题的常用方法是：敏锐地观察用题目的条件和选项方面的特征，提取有效信息，综合、判定，利用特殊化与一般化思想、正向思维与逆向思维辩证处理，或从问题成立的必要条件出发，排除不可能的选项，先排除后再求解，获得简捷有效的解题途径.

思考1：（2000年高考题）过抛物线y=ax（2a＞0）的焦点F，作一直线交抛物线于P、Q两点，若PF=p，QF=q，则+=（）.

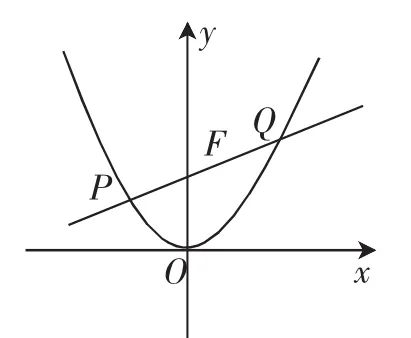
图1

图2

解析：由选项特征，结果是与直线斜率无关的定值，不管直线如何运动，+是定值，于是取斜率为0的直线，由抛物线的定义，知p=q=，易得答案D.

还可以从极限原理出发，思考直线的极限位置，当直线的倾斜角无限接近直角时，y轴是它的极限位置，所以=4a，=0.

视角2：构造思想，不等式法

当从问题的条件得到结论的一般性方法直接推导遇到困难，甚至不能可解决时，通过观察、联想、整合、重组、变换等构建一个熟悉的关系，使抽象的问题显性化，使复杂的问题简单化，从而把问题解决，这种方法称为构造性解题方法.利用平均值不等式求最值是最干脆利索而且应用十分广泛的一种方法，但许多最值问题并不能直接地使用基本不等式，必须合理折项、添项或配凑变形，创造应用平均值不等式的环境.其中有些最值问题是变量较多的多元最值问题.通常先用平均值基本不等式进行合理放缩减元，最后得到定值，然后检验等号能否取得.本题属于二元最值问题.

A.a2+b2≤1 B.a2+b2≥1

解析：由M（cosθ，sinθ）的特征，构造圆x2+y2=1，由题意圆心（0，0）到直线bx+ay-ab=0的距离不大于半径1，即≤1，平方得，故选D.

视角3：降维思想，消元法

在解决数学问题的过程中，经常碰到多元问题，利用已知条件通过消元方法，降低为一元问题，达到把多元复杂问题转化为简单问题的目的.它是实施化归思想的重要方式和手段，在帮助学生解决函数与方程、最值与范围等问题时有着广泛的应用.本题属于将二维问题转化为一维问题.

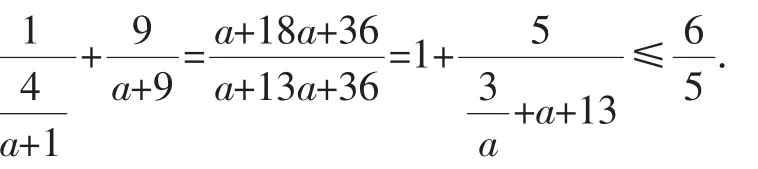
思考3：已知a2+8b2=kb（a+b）对所有实数a，b总成立，求实数k的取值范围.

解析：除参数k外，仍有两个变元，考虑到等式是关于a，b的齐次结构，变为一元问题处理，当b=0时，显然不是恒等式，于是）2+8=k+1），令=t，问题就转化为关于t的一元二次方程t2-kt+8-k=0有解的问题，由Δ= k2-4（8-k）≥0，解得-8≤k≤4.

视角4：转化思想，换元法

换元法在解高考试题中有非常广泛的应用，根据题设条件，进行合理的代换，可以使字母之间的关系更清楚，还可以改变研究式的结构特征，为综合运用其他方法和有关知识创造条件.因此，常能起到化繁为简、化难为易的作用.

思考4：（2013年高考题）已知函数f（x）=（1-x2）（x2+ax+b）的图像关于直线x=-2对称，求f（x）的最大值.

解析：利用对称，f（-1）=f（-3），f（1）=f（-5），得到a= 8，b=15，f（x）=（1-x）（1+x）（x+3）（x+5），f（x）=［（x+2）2-1］· ［9-（x+2）2］，以x+2为基本量换元，令（x+2）2=t，则y=（t-1）· （9-t）=16-（t-5）2，故最大值为16.

视角5：对称思想，变换法

对称是普遍的自然现象，它代表了简单、和谐，给人以美的享受.对称问题在数学中大量存在，如图像的对称性、代数式结构的对称性、思维方式的对称等.对称是人们思考问题的一种方式，给人以思想的启迪，给人以美的享受.

美国著名数学家波利亚曾说：“从一般意义上讲，对称对于我们探索怎样解题是很重要的，如果题目具有某方面的对称性，我们常常能得益于注意到可以互换的部分，而且，常常值得我们用同样的方式来处理那些起相同作用的部分.”可见，对称是一种思考问题的方式与策略.

A.90度 B.60度 C.45度 D.30度

分析：由题设，a，b互换，同时A，B互换，等式不变，利用对称美，必有A=B，原等式转化为，即sinC=1，A=B=，可以迅速获取答案C.

三、问题推广

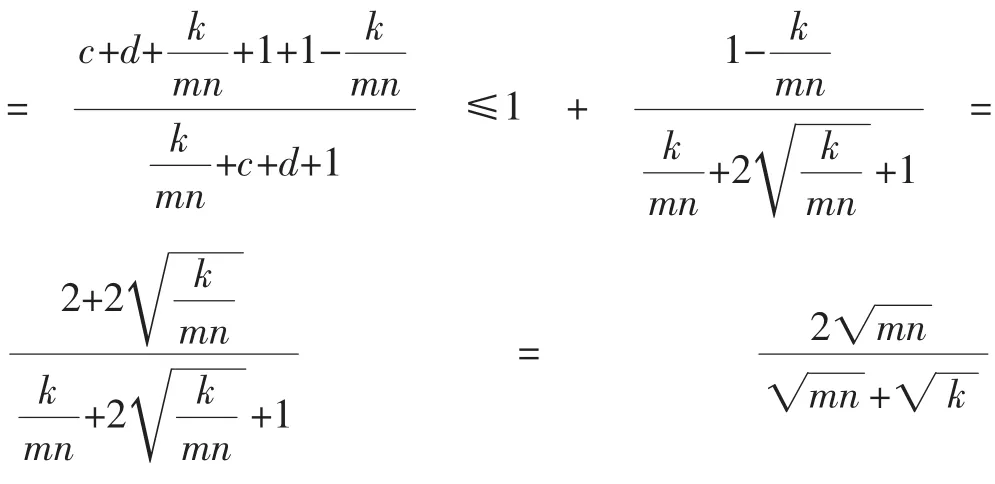
四、教学反思

1.揭示数学本质，注重基本方法的落实

数学学习强调探究，探究解决问题的基本方法，就本题而言，复杂问题简单化，由已知条件，化二元为一元化，就是通法.利用不等式求最值，也是最常见的方法之一，巧妙使用不等式能使问题的解决干脆利索.小题小做是智慧的象征，是辩证法的胜利.换元法是最基本的数学方法之一，在百思不解时，可能是一剂灵丹妙药，让你有柳暗花明又一村之感.如1993年数学竞赛题：已知x，y是实数，4x2-5xy+4y2=5，S=x2+y2，求S最大值与最小值的倒数之和，可以考虑换元法，令，转化为一个三角函数式的最值问题.

2.精选习题，提炼方法

教师在平时教学中，注重习题的典型性、可探究性和可创造性.在习题分析过程中，教师要学会“示弱”，给学生充分的时空思考，发表自己的见解，允许他们犯错误，同时也要发挥教师的“主导作用”，不愤不启，不悱不发，达成解决问题的方法后，教师要加以总结，提炼解决问题中蕴含的数学思想方法，以深化理性认识，比如，消元法、换元法等.在解题教学中，常重视技巧的训练，缺失思想的引领，如何沟通已知与未知之间的联系，其本质是利用一切手段，转化为一个简单问题.如2011年江苏卷理第13题：设1=a1≤a2≤…≤a7，其中a1，a3，a5，a7成公比为q的等比数列，a2，a4，a6成公差为1的等差数列，则q的最小值是________.本题叙述简单，内容繁杂，若陷入微观思考，不易解决.抓住必要条件a6≤a7，由题意，a6=a2+2， a7=q3，且a2≥1，所以q3≥a2+2≥3，即q≥，此时1≤适合题意，所以q的最小值是

在教学中要重视对思维过程的分析，特别是考试过程中学生暴露出的问题，应结合课堂教学深入分析，分析问题形成的原因，分析教学中存在的问题，不要只是追求题量，更重要的是对所做习题的深入思考，渗透习题求解过程中蕴含的数学思想.要知道，慢下来才会有“风景”.

3.渗透美学教育，引入哲学思考

数学家们把欧拉公式eiπ+1=0视为最优美的公式，美在哪里？我们知道数学中有五个最有代表性的数1，0，i，π，e，其中，1”、“0”代表算术，i代表代数，π代表几何，e代表分析.这五个数被欧拉用两个数学符号统一在一个等式中，确实美妙之至.在推导椭圆方程的过程中，为了美化方程，令a2-c2=b2，使方程更加整齐、对称与和谐.观察等式ab=4与式子的特点，等式中a，b对称，但“和式”不对称，利用转化思想，作一变换，令a=9c，可得，使变形后的式子美观且对称.追求美是人类的天性.追求自然、和谐、对称、简捷、奇异等是学生价值取向，感悟到数学学习中所蕴含的美学意义、美学情趣与美学精神，一定会使他们在对数学美的赏析中，享受数学学习的快乐.

1.陆贤彬，朱占奎.联系 拓展 创新——高考模拟试卷评讲的一种尝试［J］.中学数学教学参考（上），2012（5）.

2.赵善华.高中数学复习中的探究与创新［J］.数学通讯（下），2013（11）.

3.王新宏.探究特殊与一般思想在高考中的应用［J］.中学数学（上），2016（2）.