列车振动荷载作用下交叉盾构隧道动力响应与损伤分析

黄　希，晏启祥，陈　诚，李彬嘉（.西南交通大学 交通隧道工程教育部重点实验室，四川 成都　6003；.中国电建集团成都勘测设计研究院有限公司，四川 成都　6007）

列车振动荷载作用下交叉盾构隧道动力响应与损伤分析

黄希1，晏启祥1，陈诚2，李彬嘉1
（1.西南交通大学 交通隧道工程教育部重点实验室，四川 成都610031；2.中国电建集团成都勘测设计研究院有限公司，四川 成都610072）

针对交叉盾构隧道，考虑混凝土非线性特性，采用混凝土塑性损伤本构模型，在列车轮轨上施加随时间变化的现场实测振动荷载，模拟了列车在隧道中行驶的全过程，分析了速度350 km/h高速列车作用下交叉盾构隧道动力响应与损伤特性。研究表明：列车高速行驶过程中结构的应力与损伤主要集中在隧道中部区域；列车高速行驶于上部隧道时下部隧道受到的应力较小；隧道结构的拉致损伤大小和范围明显大于压致损伤；隧道的压致损伤和拉致损伤主要分布在隧道底部约130°的区域，且拱底位置损伤较大。

交叉隧道；列车振动；动力响应；损伤特性

随着我国立体现代化交通体系的快速发展，交叉隧道结构大量出现。这种交叉结构在高速列车荷载长期作用下极易出现应力集中，衬砌混凝土不断劣化，最终造成结构的破坏失效。因此研究交叉隧道结构的动力响应与损伤特性尤为重要。

目前，已有一些国内外专家针对交叉隧道结构进行了动力分析。VROUWENVELDER［1］采用二维隧道模型，对高速列车振动下的道床、隧道侧墙以及地表的动力学响应进行了仿真计算；张玉娥等［2］在现场试验的基础上，利用频谱分析获得了地铁列车引起的轨道振动加速度的数定表达式；陈卫军等［3］对上海明珠线二期盾构隧道上、下行近距离交叠隧道进行了三维弹塑性列车振动响应分析；高峰等［4］以深圳地铁近距离重叠隧道为背景，研究地铁运营期间列车振动荷载对隧道结构的影响；白冰等［5］研究了列车振动荷载作用下，由左右平行隧道逐渐过渡到上下平行隧道的复杂地铁结构的三维弹性动力响应；贾颖绚等［6］以宣武门地段复杂的空间三线交叠隧道为背景，研究了列车振动荷载作用下隧道结构的动力响应；凌昊等［7］在对深圳地铁重叠隧道各典型断面现场振动加速度测试的基础上，分析了隧道结构各典型断面的动力特性；丁祖德等［8］以有限差分法为理论基础，建立了隧道-围岩相互作用的动力计算模型；黎杰等［9］以交叠隧道为背景，研究了双向列车的行驶效应。

从以上研究可以发现，国内外学者对交叉隧道的研究主要采用弹塑性模型；列车振动荷载主要通过荷载数定法来确定。因此，本文考虑混凝土非线性力学特性，采用混凝土塑性损伤本构模型和实测的列车振动荷载，对交叉盾构隧道的动力响应与损伤特性进行分析，以便为交叉隧道结构的设计提供指导。

1　损伤分析理论

塑性流动、微裂缝和微孔洞是混凝土材料呈现非线性的根本原因，宏观上表现为混凝土抗拉强度和抗压强度的明显差异、混凝土的残余变形等［10］。为了更好地模拟混凝土受到外荷载作用后材料的非线性特性，本文采用基于连续介质的混凝土塑性损伤本构模型（CDP模型）。该模型采用各向同性弹性损伤理论结合各向同性拉伸和压缩塑性理论表征混凝土的非弹性行为，可以较好地模拟混凝土在动态加载作用下的力学响应［11］。依据《混凝土结构设计规范》（GB 50010—2010）［12］，可得到混凝土受拉损伤因子dt和受压损伤因子dc。

混凝土受拉时

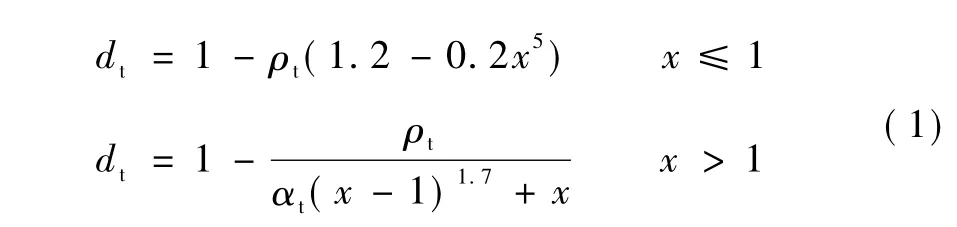
其中：

式中：ε为应变；ft为峰值拉应力；εt为与峰值拉应力对应的峰值拉应变；Ec为混凝土弹性模量。

混凝土受压时

其中：

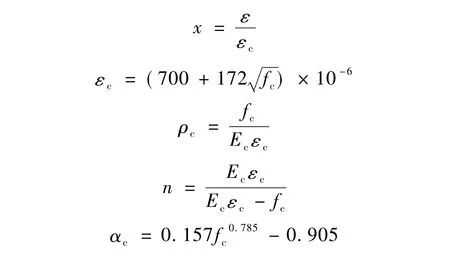
式中：fc为峰值压应力；εc为与峰值压应力对应的峰值压应变。

式中，σt为混凝土受拉应力。

式中，σc为混凝土受压应力。

2　交叉盾构隧道分析模型

以某铁路水下隧道为依托工程，计算模型中设置上下2条隧道。上部隧道沿模型长度方向设置，总长度1 500 m，其中进口段和出口段长度均为250 m，洞身段长度为1 000 m，隧道埋深70 m；下部隧道总长度100 m，与上部隧道呈空间交叉垂直关系，垂直间距14.4 m。交叉盾构隧道模型见图1。为更好地展现交叉结构相互作用关系将隧道的进出口段弱化。上下两条隧道设计时速 350 km/h，外直径 10.8 m，内直径9.8 m，管片厚度0.5 m，采用C50混凝土材料，抗渗等级S15。计算模型总长度为1 500 m，其中进口段和出口段尺寸均为250 m（长）×100 m（宽）×72 m（高），洞身段尺寸为1 000 m（长）×100 m（宽）×150 m（高），如图2所示。

图1　交叉盾构隧道模型

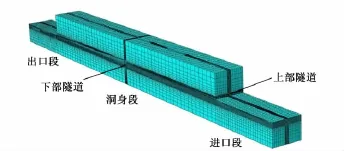
图2　有限元计算模型

该交叉隧道结构处于Ⅴ级弱风化泥质粉砂岩中，隧道衬砌采用C50高强混凝土。围岩、轨道与衬砌的物理力学参数见表1。隧道支护结构采用混凝土塑性损伤本构模型（包含压致损伤和拉致损伤），根据上述公式（1）～公式（4），可获得ABAQUS塑性损伤模型中应力与非弹性应变的关系以及损伤因子与非弹性应变的关系。轨道和列车采用线弹性模型；围岩则采用带阻尼的摩尔-库伦弹塑性本构模型。模型底部、四周设置人工粘弹性边界，较好地解决了土体-结构动力相互作用中的近场波动问题。

表1　物理力学参数

列车振动荷载受到车轮偏心、车轮擦伤、车轮踏面几何不圆顺、轨道几何不平顺等因素的综合作用，具有不确定性。因此为了更为准确地描述列车实际振动效应，通过现场实测，得到了列车以350 km/h速度行驶时的振动荷载。列车振动荷载曲线如图3所示。

图3　列车以350 km/h速度行驶时振动荷载曲线

本文模拟了高速列车在上部隧道行驶的全过程，模型中编组列车共10节车厢，每节车厢长度为25 m。为了反映列车行驶过程中的空间位置变化、振动荷载时程变化，本文对编组列车施加350 km/h的行驶速度，并在列车轮轨上施加随时间变化的现场实测振动荷载，如图4所示。

图4　列车振动荷载施加示意

3　交叉隧道动力响应与损伤分析

模型中列车以350 km/h的速度行驶在上部隧道中，因此本文着重分析上部隧道的动力响应与损伤特性。

3.1交叉隧道结构的应力时程分析

在上部隧道拱底设置3个分析点A1，A2和A3，（A2位于上部隧道中间截面的底部，A1与A3分别位于距中间截面250 m处截面的底部），在下部隧道中间截面拱顶设置B1分析点，如图5所示。

图5　分析点布置示意

分别提取交叉隧道结构4个分析点（A1，A2，A3 和B1）的竖向应力，并绘制竖向应力时程曲线，见图6。其中第3.0 s约为列车即将驶入隧道的时刻；第6.5 s为列车中间车厢刚好行驶至隧道中间截面的时刻，第10.0 s为列车即将驶离隧道的时刻。

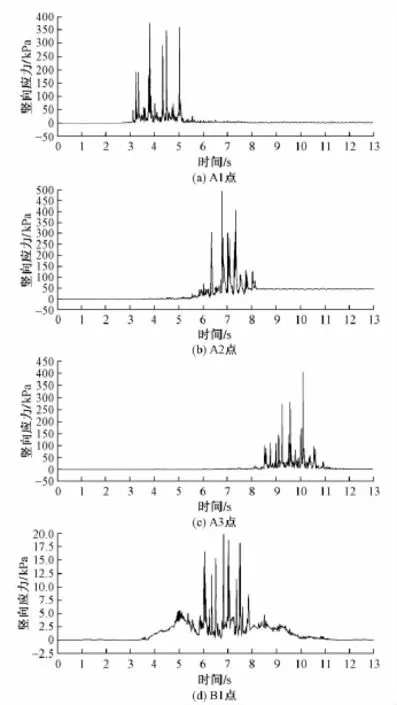
图6　分析点竖向应力时程曲线

从图6可以看出：A1为上部隧道的第1个四分点，在约3.1 s开始振动，应力峰值约为0.350 MPa，在约5.1 s振动逐渐减弱；A3点为上部隧道的第2个四分点，在约8.5 s开始振动，应力峰值约0.413 MPa，并于10.7 s左右逐渐减弱；A2点位于隧道内中间截面，在约5.5 s开始振动，应力峰值约0.498 MPa，在8.2 s左右逐渐减弱，在一定应力水平上小幅波动，并保持一个振动基准值（残余应力），约为0.049 MPa；B1位于下部隧道中间截面，在约4.0 s开始振动，并于9.4 s左右振动逐渐减弱，应力峰值约为0.020 MPa。

对比A1～A3应力时程曲线，A2点竖向应力峰值最大，A3次之，A1最小，说明应力主要集中在隧道的中部区域，且隧道出口位置的峰值应力较进口位置有一定程度的增加。对比4个分析点的应力时程曲线可知，无列车行驶的下部隧道中间截面拱顶位置竖向应力峰值仅为0.020 MPa左右，约为A2应力峰值的4%。

3.2上部隧道结构的损伤分析

对计算结果进行初步分析，可知列车高速驶过隧道的整个时间段内，所产生的损伤效应主要集中在有列车行驶的上部隧道，而与其近距离垂直交叉的下部隧道未产生塑性损伤。因此，在列车行驶的上部隧道布设3个分析截面（截面b为中间截面，截面a、截面c距离中间截面250 m）。此外为了分析方便，对分析截面进行单元标号（非有限元编号），如图7所示。列车高速行驶过上部隧道后，提取分析截面各个单元中心处的塑性损伤值，绘制出不同截面的塑性损伤雷达图（包括压致损伤雷达图、拉致损伤雷达图），如图8、图9所示。

图7　分析截面及其单元位置示意

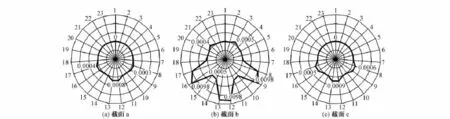
图8　分析截面压致损伤雷达图

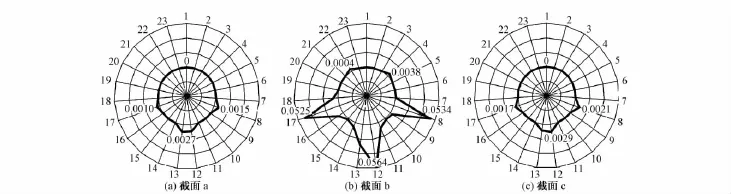
图9　分析截面拉致损伤雷达图

由图8可知：压致损伤主要分布在隧道底部约130°的区域（8～17号单元）。截面a、截面c顶部均未出现损伤，在隧道拱腰损伤开始出现，在拱底处达到最大值，分别为8.0×10-4，9.0×10-4，其中靠近出口的截面c损伤值有一定程度的增加；上部隧道的中间截面b受到下部隧道的影响损伤值明显增大，在拱腰和拱底处损伤值最大，达到9.8×10-3，约为截面a的12倍。此外，隧道拱顶也出现了一定程度的损伤。

由图9可知，截面a、截面b、截面c产生的拉致损伤分布范围与压致损伤相似，主要分布在隧道截面的中下部区域。截面a、截面 c的拉致损伤分布较为一致，损伤在拱腰附近8号、17号单元处产生，在拱底达到最大，截面 a、截面 c的最大损伤值分别为2.7× 10-3，2.9×10-3，靠近出口的截面c损伤值相对截面a有一定程度的增加；上部隧道的中间截面b受到下部隧道的影响损伤值明显增大，拱底处损伤值最大，约为5.64×10-2。此外，截面 b拱顶也出现了一定程度的损伤。

对比图8和图9可知，隧道的拉致损伤分布规律与压致损伤较为一致，但隧道的拉致损伤值约为压致损伤值的6倍，这也证明了混凝土的受拉敏感性。

4　结论

1）混凝土塑性损伤模型能更好地模拟混凝土受拉、受压时的不同表现以及混凝土的不可恢复变形等特性。

2）对于盾构隧道结构，列车行驶过程中隧道的应力、拉致损伤和拉致损伤主要集中在有列车行驶隧道的中部区域。

3）从应力角度来看，在上部隧道中行驶的列车对下部隧道的影响很小。

4）隧道的拉致损伤大小和范围均明显大于压致损伤，证明了混凝土的受拉敏感性。

5）隧道的压致损伤和拉致损伤分布规律较为一致，主要分布在隧道底部约130°的区域，且隧道拱底的损伤值较大，这是隧道设计中需要重视的。

［1］VROUWENVELDERT.TheFundamentalsofStructural Building Codes［C］//Proceedings of the International Conference on Structural Engineering.South Africa：Mechanics and Computation，2001：183-193.

［2］张玉娥，白宝鸿.地铁列车振动对隧道结构激振荷载的模拟［J］.振动与冲击，2000，19（3）：68-70.

［3］陈卫军，张璞.列车动载作用下交叠隧道动力响应数值模拟［J］.岩土力学，2002，23（6）：770-774.

［4］高峰，关宝树，仇文革，等.列车荷载作用下地铁重叠隧道的响应分析［J］.西南交通大学学报，2003，38（1）：38-42.

［5］白冰，李春峰.地铁列车振动作用下交叠隧道的三维动力响应［J］.岩土力学，2007（增）：715-718.

［6］贾颖绚，刘维宁，孙晓静，等.三维交叠隧道列车运营对环境的振动影响［J］.铁道学报，2009，31（2）：104-109.

［7］凌昊，郑余朝，仇文革，等.深圳地铁重叠隧道列车振动响应测试与数值分析［J］.城市轨道交通研究，2010，13（8）：49-53.

［8］丁祖德，彭立敏，雷明锋，等.高速铁路隧道列车振动响应影响因素分析［J］.铁道科学与工程学报，2011，8（4）：1-6.

［9］黎杰，李欢，霍飞.列车振动荷载作用下交叠隧道衬砌结构响应特性分析［J］.公路工程，2012，37（1）：40-42.

［10］李杰，吴建营.混凝土弹塑性损伤本构模型研究Ⅰ：基本公式［J］.土木工程学报，2005，38（9）：14-20.

［11］晏启祥，李彬，张蒙，等.200 km·h-1列车脱轨撞击作用下盾构隧道二次衬砌对管片衬砌的防护效果［J］.中国铁道科学，2014，35（6）：70-78.

［12］中华人民共和国建设部.GB 50010—2010混凝土结构设计规范［S］.北京：中国建筑工业出版社，2010.

［13］张战廷，刘宇锋.ABAQUS中的混凝土塑性损伤模型［J］.建筑结构，2011（增）：229-231.

（责任审编葛全红）

Dynamic Response and Damage Analysis of Spatial Intersecting Shield Tunnels Under Vibration Load of Train

HUANG Xi1，YAN Qixiang1，CHEN Cheng2，LI Binjia1
（1.Key Laboratory of Transportation Tunnel Engineering of Ministry of Education，Southwest Jiaotong University，Chengdu Sichuan 610031，China；2.Powerchina Chengdu Engineering Corporation Limited，Chengdu Sichuan 610072，China）

For spatial intersecting shield tunnel，the field measured vibration load changing with the time was applied on the wheel and rail of the train by considering the nonlinear characteristics of concrete and adopting the plastic damage model of concrete，the train running process in the tunnel was simulated and the dynamic characteristics and damage properties of the intersecting shield tunnel were analyzed under the action of high speed train with 350 km/h.Research results show that stress and damage of the structure are mainly concentrated in the middle area of the tunnel during the high speed train traveling，the lower tunnel has less stress when the train is running in the upper tunnel，the tension-induced damage degree and extent of tunnel structure is significantly larger than the compression-induced damage，both damages are mainly distributed at 130°region of the tunnel bottom，and the damage at the arch bottom is relatively large.

Spatial intersecting tunnel；T rain vibration；Dynamic response；Damage property

TU93；U451+.3

A

10.3969/j.issn.1003-1995.2016.08.15

1003-1995（2016）08-0060-05

2016-03-10；

2016-06-05

国家自然科学基金（51278425，51178400）；中国铁路总公司科技研究开发计划（2014G004-H）

黄希（1991— ），男，硕士研究生。