连续梁桥平转施工称重试验方法优化研究

苏巨峰，李　磊，黄　健，任　翔（.长安大学 桥梁结构安全技术国家工程实验室，陕西 西安　70064；.中铁十局集团有限公司，山东 济南　500；.西安科技大学 建筑与土木工程学院，陕西 西安　70054）

连续梁桥平转施工称重试验方法优化研究

苏巨峰1，李磊2，黄健2，任翔3
（1.长安大学 桥梁结构安全技术国家工程实验室，陕西 西安710064；2.中铁十局集团有限公司，山东 济南250101；3.西安科技大学 建筑与土木工程学院，陕西 西安710054）

基于张（家口）呼（和浩特）客运专线兴和特大桥平转施工前称重试验，对连续梁称重试验过程中的测点布置、数据处理、配重方案等相关问题进行研究，提出对既有称重试验方法的优化建议，以提高称重试验的效率和精度。研究结果表明：将位移传感器布置在球铰侧面测量水平位移优于布置在撑脚附近测量竖直位移；称重试验时可通过顶升力时程曲线快速得到称重试验的临界力；转动球铰法称重试验对于球铰具有润滑作用，试验时顶升次数不宜太少，建议每侧至少进行3次；对于球铰转动摩阻较小的连续梁，建议采用撑脚落地接触滑道的转动姿态进行转体，并根据该方案配重。

连续梁；平转施工；称重试验；摩阻力矩；配重方案

在桥梁转体施工中，转体系统必须具备易转动和安全稳定这2个基本条件。通常在桥梁转体前进行结构称重试验，对转体结构及转动系统转体前的实际状态进行测试，得到结构的不平衡力矩、重心偏心距、球铰的静摩阻力矩等，据此对结构进行配重以及预测启动牵引力的大小，保证桥梁结构按照预定的目标平顺、可靠地转体到位［1-2］。

魏峰等［3］结合北京五环路转体重万吨以上的斜拉桥转动体施工，在转体前对转动体进行了部分称重试验，对称重试验的原理和一般方法进行了介绍，给出了该工程称重试验的结果和最后配重方案。张雪松等［4］结合石家庄西柏坡高速公路2×67 m曲线T构转体称重试验，介绍了称重试验中数据处理的方法，提出了该工程的平衡配重方案。鲁建生、尚高科等［5-6］结合工程实践介绍了相应工程称重试验的方法和结果。由于工程实践需要，既有文献大多结合具体工程介绍称重试验的一般步骤和相应的试验结果，涉及到的试验方法基本相似或相同，对于称重试验方法以及试验过程优化的研究相对较少。

目前，测试转动体不平衡重的主要方法有墩柱不平衡应力（应变）法、梁端挠度法、转动球铰法等［7］。墩柱不平衡应力（应变）法只能测不平衡力矩而无法求得球铰的静摩阻力矩，配重时无法考虑静摩阻力矩的影响，当静摩阻力矩较大时，转体配重结果会产生较大误差。而且不平衡力矩测试依赖于墩底截面处应力测试结果，对应力测试精度要求较高，实际应用有待进一步研究。梁端挠度法只适用于支架现浇施工的桥梁，对于悬浇法施工的桥梁则无法应用，实际应用有限。转动球铰法是目前工程实践中采用最多的称重试验方法。

本文以转动球铰法称重试验方法为研究对象，首先分析了转动球铰法称重试验的原理和既有试验方法，然后结合现场测试结果，对称重试验过程中的相关因素进行研究，最后给出针对既有称重试验方法的优化建议。

1　称重试验原理及方法

转动球铰法将整个转动体视作刚体，通过施加转动力矩，转动体将绕球铰做刚体转动，当转动体从静止状态进入动摩擦状态，即发生转动位移突变时，转动体在施加的转动力矩、不平衡力矩及静摩阻力矩3者作用下刚好处于力矩平衡的临界状态［8］，根据静力平衡方程即可求得转动体不平衡力矩。

称重试验原理示意见图1，分别在转动体的2个相对方向施加顶升力，并同时监测梁体的竖向位移，当梁体竖向位移发生突变时，表明转体已经发生转动，试验停止。根据试验结果绘制位移-力曲线，曲线斜率的突变点所对应的力即为临界力 P1，P2，顶升力作用点距球铰中心距离分别为 L1，L2，根据式（1）～式（3），计算不平衡力矩、静摩阻力矩及静摩阻系数［9］。

式中：MG为不平衡力矩；MZ为静摩阻力矩；μZ为球铰静摩阻系数；R为球铰中心转盘球面半径；N为转体重量。

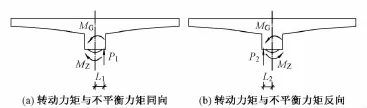
图1　称重试验原理示意

2　工程背景及试验方法

2.1工程背景

新建张呼客运专线兴和特大桥主桥跨张集铁路，为（48+80+48）m的预应力混凝土连续梁结构，施工方法为先在铁路两侧悬臂浇筑施工，然后通过平面转体合龙，设计平面转体32°。兴和特大桥主桥转体系统（见图2）分别设置在19#和20#桥墩墩顶，由下转盘、球铰、上转盘、转体牵引系统等组成。单个转动体设计总重量为36 750 kN，球铰采用钢球铰，转动半径3.05 m。为了减小球铰摩阻，在下球铰面内镶嵌MPG滑片并涂抹黄油。在上转盘距离球铰中心2.2 m处环向对称设置4组钢撑脚，下转盘对应位置设置滑道。

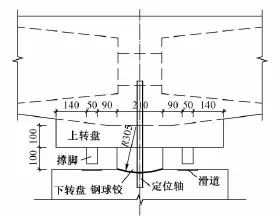
图2　兴和特大桥转体系统（单位：cm）

2.2试验测点布置

试验采用机电百分表测试位移，在球铰两侧各对称布置2个，其中1#和2#按照常规做法布置在撑脚上，测试球铰转动时撑脚的竖直位移，增设的3#和4#传感器布置在球铰侧面，测试球铰转动时球铰侧面的水平位移。通过油压千斤顶施加顶升力，百分表及千斤顶布置示意见图3。

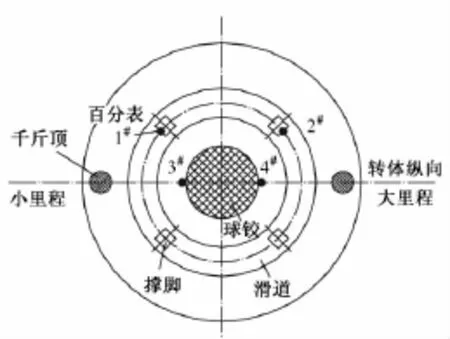
图3　称重试验仪器布置示意

顶升力的精确测试依靠千斤顶上布置的压力传感器实时测量，测量结果与标定过的油压表读数进行对比，相互校核。

2.3试验方法

试验开始前，清理撑脚及滑道，逐步对称解除支座处的临时支撑，注意观察撑脚是否随临时支撑的解除连续向一侧下沉，据此判断转动体系的平衡状态。按照上述的测点安装仪器后，先施加一个较小的顶升力进行试顶，观察仪器及测试系统是否正常工作，检查各项工作指标正常后，卸载至零，进行位移和力的初读，随后试验正式开始。试验过程中连续记录各测点位移时程曲线，根据位移时程曲线判断球铰开始转动时刻，随即停止顶升并卸载，一次顶升结束。解除临时支撑后，当所有撑脚均未落地时，两侧来回顶升，每侧各顶升4次，如果一侧撑脚落地则只在撑脚落地一侧顶升8次。试验结束后，根据测试数据整理试验结果并计算配重。

3　试验结果及讨论

兴和特大桥主桥有19#和20#墩2个转动体，试验时每个转动体在纵横2个方向都进行了多次顶升测试，本文旨在讨论连续梁称重试验的一般规律，以下讨论均以20#墩转动体顶升的试验结果为例。

20#墩转动体拆除沙箱等临时约束时，未见撑脚向一侧倾斜，4个撑脚离滑道距离约20～25 mm，判断球铰静摩阻力矩大于梁体的不平衡力矩。为了得到球铰转动时的临界力，常规做法是根据测得的位移和对应时刻的力做出力-位移曲线，并进行线性拟合。由于结构从静摩擦状态进入动摩擦状态时，力-位移曲线会产生突变，突变点对应的力即为临界力。20#墩在小里程侧顶升试验结果经处理后得到的力-位移曲线见图4。由图4可知，位移传感器布置在撑脚上与布置在球铰侧面拟合出的力-位移曲线求得的临界力比较接近，均为650 kN左右。

上述数据处理方法是称重试验常见的处理方法。本文将根据测试数据，从位移传感器布置位置、临界力的判定方法、试验次序、配重方案等方面对称重试验方法进行讨论。

图4　小里程侧顶升力-位移曲线

3.1位移传感器布置位置

假设球铰处于理想的静摩擦状态，当顶升力较小时，转动力矩不足以克服球铰的静摩阻力矩，理论上整个结构不应该产生任何位移。但从图4中可以看出，顶升刚一开始，布置在撑脚处及球铰侧面的位移传感器均测试到了位移。文献［8］分析认为产生这一现象的原因是球铰之间的润滑层压缩及转动体的顶升作用。实际上，在本工程中这部分位移还应包括球铰滑动面上的构造（如MPG滑片）等引起的部分非滑动位移。由图4可知，布置在球铰侧面的4#测点，在球铰转动前几乎无位移，直到球铰转动时才产生比较明显的位移，这与理想的球铰摩擦受力状态最接近，说明该位置受非滑动位移的影响较小。与传统布置在撑脚处的2#测点相比，利用布置在球铰侧面的4#测点获得的力-位移曲线判断顶升临界力点更加容易和准确。

20#墩在两侧顶升时的位移时程曲线见图5。从图5可以看出，布置在球铰侧面的传感器得到的位移时程曲线在顶升刚开始时位移基本在0附近，直到临界点时，曲线才发生明显突变，位移从0快速偏向一侧。相对于1#，2#曲线通过斜率的变化点来判断转动时刻，显然通过3#，4#曲线的突变来捕捉转动临界点更加容易，这与图4反映的规律是一致的。所以，称重试验时为了获得准确的球铰转动时刻，将位移传感器布置在球铰侧面测量球铰转动引起的水平位移要明显优于将位移传感器布置在撑脚处测量撑脚的竖向位移。

3.2临界力的判定方法

从称重试验的原理可知，试验数据处理的核心是求得球铰转动时的顶升临界力。试验过程中同时采集了位移时程曲线和顶升力时程曲线，见图6。

结合图5和图6可知，试验开始时，球铰处于静摩擦状态，随着油压泵加压，顶升力不断增大，位移测点也发生较小的非滑动位移。在55 s左右，顶升力突然减小，而位移突然增大，二者发生突变的时刻是相同的。此后球铰进入动摩擦状态，顶升力的大小基本维持不变，而位移则持续增加，直到停止顶升。

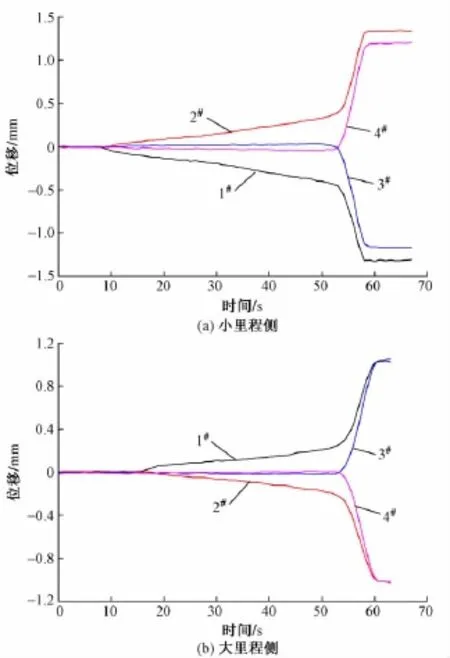
图5　位移时程曲线

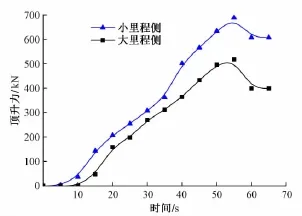
图6　顶升力时程曲线

以上分析结果表明，通过顶升力时程曲线也可以判断球铰转动的临界状态，且与位移时程曲线判断得到的临界点是一致的。一般在称重试验时，为了满足一定的测试精度，要求同一侧前后2次顶升试验所得临界力差值不能过大，否则需要重新测试。通过顶升力时程曲线可以在现场判断临界力的大小，而传统方法则需要数据拟合处理后才能算出临界力的大小，在现场无法快速判断2次测试之间的差值，故在现场较难判断称重试验的精度。

试验过程中还发现，当球铰转动时，油压表指针回落现象明显，此后继续进油，油压表几乎维持在固定的位置不再变化。因此，可以根据油压表变化控制试验进程，而位移测试作为相互校核的依据，此种方法可以提高试验的安全性。试验过程中，如果油压表读数较大而无位移发生时，应及时停止试验并检查，以排除各种干扰因素，防止试验出现危险。

3.3试验次序

为了观察试验次序对临界力的影响，20#墩试验时在纵向共进行了8次顶升试验。第1次从小里程侧顶升，球铰转动后停止试验，然后在大里程侧顶升，依次循环，每侧各4次，共8次。顶升力与测试次序关系见图7。从图7中可以看出，小里程侧第1次顶升时的临界力显著大于以后几次该侧顶升的临界力，几乎是后面几次的2倍。而第1次过后，小里程侧其他几次顶升的临界力数值都比较接近。大里程侧第1次顶升的临界力稍大于以后几次的测试结果，但差值不明显。

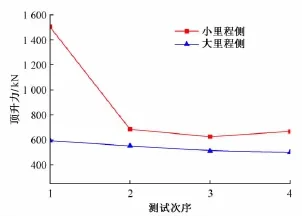
图7　顶升力与测试次序关系

试验结果表明，结构第1次转动时的摩阻力矩明显大于以后再次转动的摩阻力矩。引起这种现象的原因可能是球铰经过了长期的静置，在重压下还未得到充分润滑，加之该球铰的滑片构造在首次滑动时位置会有微小调整，导致其数值明显大于以后再次测试时的结果。试验数据处理时，建议舍去两侧第1次试验结果，取两侧各自最后2次试验结果的平均值作为最终试验结果。

由图7可知，称重试验时，来回顶升对于球铰具有润滑作用，能够减小球铰的摩阻力矩，对于转体牵引是有利的，这是采用转动球铰法相较于其他方法进行称重试验的一个优点。

3.4配重方案的确定

称重试验的最终目的是根据测试结果进行配重，以保证结构平顺、安全地转体到位［10-11］。转体时的转动姿态是影响配重方案的重要因素之一。连续梁平转施工中有2种转体姿态可供选择：一种是撑脚落地，形成撑脚与中心球铰一起受力的多点支撑转动体；另一种是经过精确配重，使转动体不平衡力矩小于球铰摩阻力矩，从而实现转体过程中撑脚全部离地只起保护作用，球铰单点支撑转动体。显然，第1种状态由于撑脚落地，将增加转动体的牵引力，但在转体过程中多点支撑，稳定性更好。第2种状态能够减小转动体的牵引力，但在转体过程中单点支撑，结构平衡主要依靠球铰的摩阻力矩，当球铰摩阻力矩较小时，这种状态的稳定性较难保证［12］。

兴和特大桥采用了下滑动面镶嵌MPG滑片的构造，有效降低了球铰的转动摩阻。经实测，球铰转动静摩阻系数为0.021，滑动摩阻系数更小。较小的球铰摩阻，使得球铰转动更加容易，但对桥梁转体过程中的稳定性带来了一些新的问题。

根据称重试验的结果，发现20#墩球铰的摩阻力矩较小，单点支撑的平衡转体难度较大，而根据实测摩阻系数测算的牵引力与原设计的牵引系统能够提供的牵引力相比，设计富余度较大。所以，该桥决定采用重心偏向一侧且撑脚落地接触滑道的转体方案。最终通过在远离张集铁路一侧配重，使重心纵向偏离球铰中心8 cm，此时，不平衡弯矩大于球铰静摩阻力矩，远离张集铁路一侧的2个撑脚自然落地，2个撑脚和球铰形成了3点支撑，有效保证了转体过程中的稳定性。另外，此方案还能够有效抵抗横向的偶然不平衡力矩，防止转动过程中的“大翻身”。按照该方案配重后，梁体实际转动时姿态未发生变化，平稳可靠地转体到设计位置。

4　结论

1）通过测量球铰转动位移判断球铰转动状态时，将位移传感器布置在球铰侧面测量水平位移优于布置在撑脚附近测量竖直位移。

2）连续梁平转施工法的称重试验，建议采集顶升力时程曲线。

3）通过观察油压表指针可以判断梁体的转动状态，建议试验过程中根据油压表的变化控制试验进程，可以提高试验过程的安全性。

4）转动球铰法称重试验对于球铰具有润滑作用，测试时建议每侧至少进行3次顶升。

5）对于球铰转动摩阻较小的转体结构，在牵引力足够的情况下，建议优先采用撑脚落地接触滑道的转体方案。

［1］张联燕，程懋方，谭邦明，等.桥梁转体施工［M］.北京：人民交通出版社，2003.

［2］涂杨志.跨武广特大桥转体连续梁设计［J］.铁道工程学报，2012（11）：43-48.

［3］魏峰，陈强，马林.北京市五环路斜拉桥转动体不平衡重称重试验分析［J］.铁道建筑，2005（4）：4-6.

［4］张雪松，王慧东.西柏坡高速2×67 m同步转体曲线T构称重试验研究［J］.石家庄铁道大学学报（自然科学版），2013，26（3）：23-26.

［5］鲁建生，杨永宏，刘继龙.保阜高速公路跨京广铁路转体桥称重试验研究［J］.铁道建筑技术，2009（5）：106-109.

［6］尚高科.连续梁桥平转施工称重试验研究［J］.国防交通工程与技术，2013（增1）：30-31，8.

［7］郭子仪，陈小佳，郑舒月，等.转体施工转动体系不平衡力矩测试方法研究［J］.公路工程，2014，39（3）：73-76，82.

［8］陈顺超，黄平明，王吉磊.桥梁平转施工称重试验及启动牵引力计算探讨［J］.铁道建筑，2011（11）：20-22.

［9］赵勇为.转体施工中连续刚构梁桥力学特性分析［D］.兰州：兰州交通大学，2013.

［10］铁道部经济规划研究院.TZ 324—2010铁路预应力混凝土连续梁（刚构）悬臂浇筑施工技术指南［S］.北京：中国铁道出版社，2010.

［11］中华人民共和国铁道部.铁建设［2010］241号高速铁路桥涵工程施工技术指南［S］.北京：中国铁道出版社，2010.

［12］董琴亮.跨既有铁路线大跨连续梁桥转体施工与控制技术［J］.中外公路，2014，34（4）：143-147.

（责任审编郑冰）

Study on Optimization of Weighing Test Method for Continuous Girder Bridge Constructed by Horizontal Rotation Approach

SU Jufeng1，LI Lei2，HUANG Jian2，REN Xiang3
（1.National Engineering Laboratory for Bridge Structure Safety Technology，Chang'an University，Xi'an Shaanxi 710064，China；2.China Railway No.10 Engineering Group Co.，Ltd.，Jinan Shandong 250101，China；3.School of Architecture and Civil Engineering，Xi'an University of Science and Technology，Xi'an Shaanxi 710054，China）

Based on the weighing test of Xinghe super-large bridge on Zhangjiakou-Huhehaote high speed railway，the test method of measuring points arrangement，data processing and the principle of counterweight scheme were examined.T he results show that arranging displacement sensor for measuring horizontal displacement on the side of the ball joint is better than that of vertical displacement measured near the balance brace.It is suggested that the critical load of weighing test can be acquired directly from the force-time curve.T he weighing test method of rotating ball joint has an effect of lubrication to the ball joint，therefore，the number of test should not be too little，every side do the test three times at least is suggested.For the ball joint of continuous beam with low friction，the rotation posture of balance brace landing on the circular track is recommended，and the counterweigh scheme should be calculated according to the requirement of this posture.

Continuous girder；Horizontal rotation construction；W eighing test；Frictional torque；Counterweight scheme

U448.21+5

A

10.3969/j.issn.1003-1995.2016.08.03

1003-1995（2016）08-0014-05

2016-03-01；

2016-05-20

中国铁建大桥工程局集团有限公司基金（Cr13gk-2013-19）；国家自然科学基金（51408484）；陕西省教育厅科研计划（14JK1488）

苏巨峰（1984— ），男，博士研究生。

任翔（1979— ），男，副教授，博士。