引导经历过程 丰富“直接经验”
赵斌
史宁中校长在《课标修改后小学数学教学的变化》的讲话明确指出:“中国未来小学数学教育将转入更加注重内涵的改革深化阶段:其一,注重思考力的培养;其二,注重过程性经验的积累;其三,注重真正意义上的‘理解’。”第二点中对“过程性经验”的注重,一方面凸显了“过程”对于经验积累、思考力培养和意义理解的价值,另一方面也强调了“直接经验”的积累。由此可见,现行课程标准更强调让学生经历数学活动的全过程,强调直接经验对于学生全面发展的重要性。
那么,什么是“直接经验”呢?所谓直接经验,是指通过亲身参与实践活动而获得的知识。在数学学习中,直接经验则是指学习者通过自身主动的观察、操作、比较、抽象、分析、概括等数学活动而获得的数学知识、数学方法、数学思想以及数学活动经验。直接经验更强调学习者亲力亲为的活动过程,在活动过程中习得知识、建构方法。但这还不够,学生在活动中获得的经验还要予以提升、丰富,以从中感悟数学思想方法,形成积极的情感态度与价值观,最终提升学生的数学素养。
在数学课堂教学中,我们又该如何帮助学生积累“直接经验”,并对其进行提升和丰富呢?笔者认为,需要注重以下几方面:
一、经历知识发生、发展过程,积累自主建构知识的经验
数学知识是沿着一定的内在逻辑顺序延伸,形成了严密的知识体系,这一知识体系是在前人不断摸索、优化、创新的过程得以不断完善和丰富的。《义务教育数学课程标准》(2011年版)强调:“数学学习要让学生能体会数学知识之间的联系,了解数学的价值,提高数学学习的兴趣,增强学好数学的信心,养成良好的学习习惯,具有初步的创新意识和科学态度。”这就要求我们的教学要设计、组织好数学活动,引导学生积极参与数学活动,经历知识体系的完善和延伸过程,在此过程中感受知识的价值,体会数学知识之间的联系,主动构建、内化数学知识,积累数学优化和创新的经验,培养创新意识。
【案例1】复式统计表
(教师将学生分成6组,组织学生自主统计各组男、女生人数,并分组制作成6张单式统计表)
教师请学生展示6张单式统计表。
师:你能向大家介绍一下你填每张统计表中的人数时的顺序吗?
生:每张统计表我都是先填男生人数,再填女生人数,最后将男生与女生的人数加起来算出合计人数。
师:请大家仔细观察你填的统计表,我们班哪组男生人数多?哪组女生人数多?从6个统计表中能很清楚地看出来吗?
学生自觉活动:有的学生一张张翻看6张统计表,还有的学生将6统计表纵向排列对比。
生:第2组的男生最多,第5组的女生最多。
师:怎么比较出来的?
生:我将这几张表的男生人数、女生人数对齐排好,很快就比出来了。
师:这6张统计表每张都反映了每组同学的人数情况,这是我们以前学习的单式统计表,但如果要将不同组的人数情况进行对比或了解一些总体人数情况就比较麻烦,怎么办呢?
生:可以把6个单式统计表合起来编成一个统计表。
师:是的,把几张单式统计表合编而成的统计表我们把它叫作复式统计表,这也就是今天我们要一起研究的内容。(板书课题)下面,我们一起根据刚才的统计,来制作一张复式统计表。
师:通常,制作一张统计表先要有哪些部分呢?如果让你合成一张统计表,竖的你会划分成哪些栏目?横的呢?(结合学生回答板书)
师:谁愿意来指导一下老师,该怎样进行填写?(请一生上台指导,教师板书)
师:现在从这张统计表中能清楚地看出每组男女生人数和各组总人数了吗?
生:能!
师:能清楚地看出我班男生一共多少人吗?
生:不能!
师:那怎么办呢?
生:可再添上一行合计栏。
师:你的想法很好!我们可以在表中加入一栏,但为了避免重复和混淆,这一横栏叫作总计栏。(板书)现在男生总人数怎么算呢?女生呢?
生:……
师(小结):所以复式统计表不光要横着看,还要竖着看。
师:这张统计表完成了吗?你知道这个空格(合计栏)里是什么人数吗?
生:这里填全班的总人数。
师:全班总人数可以怎么算呢?
生1:全班人数就是将第1、2、3、4、5、6组的合计人数全加起来。
生2:我觉得也可以将男生合计人数和女生合计人数加起来。
师:猜一猜,两种算法结果相同吗?
生(齐答):相同!
请学生用两种方法口算出结果,并验证。
师:如果两种算法结果不同呢?
生:那就说明肯定有什么地方算错了,就要重新算一下。
师:所以算好后就可以用另一种方法进行验算。
引导学生观察统计表有没有完成,认识“表头”。
……
一般认为,复式统计表结构是规定的,但这种规定从其内部分析有着一定的规则,这些规则产生于人们对单式统计表在一些特定情境下所体现出的劣势的弥补和优化,体现了人类为适应社会生产和日常生活所作出的创新,这也是复式统计表的内在价值。学生能通过活动产生对单式统计表不足的内在需求,并积累从单式统计表逐步创造出复式统计表的直接经验,一方面能充分感受学习这一知识的价值,另一方面也能对复式统计表的结构有更深入的认识,从而提高对其应用能力。
因此在教学中,通过一组富有挑战性和引导性的问题:我们班哪组男生人数多?哪组女生人数多?从6张统计表中能很清楚地看出来吗?激发学生产生进一步整理数据的内需,这时就有学生将6张统计表纵向排列后进行比较,复式统计表的雏形由学生自己创造了出来,在这一过程中,单式统计表的局限性得以显现,复式统计表的价值由此凸显。然后,教师再引导学生结合自己的需要和理解,“指导”教师整合统计表,复式统计表在学生自觉的活动中进一步成型。本课虽不要求学生制作复式统计表,但整个统计表的制作都是学生在自主活动过程中逐步设计并“指导”教师完成的,学生在活动中积累了较为丰富的直接经验,提升了学生的创新意识和实践能力,并对数据分析观念的提升有一定促进作用。
二、经历数学思维的过程,积累数学化的经验
小学生的数学思维活动,是学习数学所特有的思维活动。数学教学是数学思维活动的教学,发展学生的数学思维是数学教学的核心问题。数学教学不仅要让学生在活动过程中积累行为操作经验,更应注重数学思维经验的积累,在此过程中提升学生抽象、推理、几何直观等能力,发展学生的数学思考。
【案例2】《“多边形面积的计算”单元整理和复习》
(教师引导学生通过回顾与整理,梳理出多边形的面积计算公式及各自推导过程)
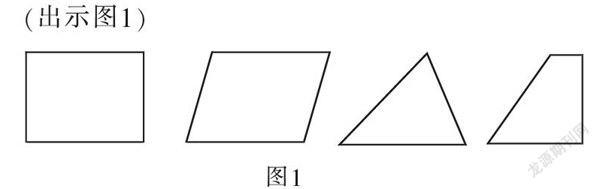
图1
师:这里4个图形的面积有怎样的关系呢?你能先看图估计一下吗?
生1:我估计长方形和平行四边形的面积相等,三角形和梯形的面积相等。
生2:我的估计和他差不多,我再补充一点:三角形和梯形的面积大概是长方形面积的一半,也大概是平行四边形面积的一半。
师:要准确比较出这些图形面积的大小,你准备怎么办?
生:要准确比较它们的大小,就要量出长度,算出它们的面积,再比较。
师:(出示点子图,如图2)现在,你能看出决定它们面积大小的长度吗?
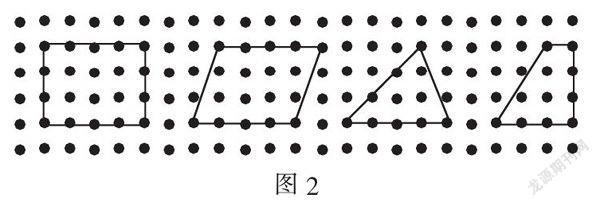
学生回答出各图形相关边的长度是几格,分步出示图3:
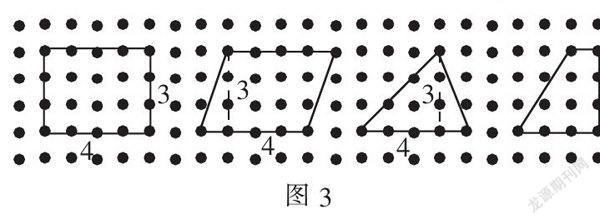
师:到这一步,如果让大家计算,我相信大家都能比较出这四个图形面积的大小,但你能不用计算,很快看出它们面积之间的关系吗?先看这两个图形。(出示长方形、平行四边形)
生:长方形和平行四边形面积相等。
师:能介绍你的想法吗?
生:因为长方形的长和平行四边形的底相等,宽和平行四边形的高相等,长方形的面积计算公式是长乘宽,平行四边形的面积计算公式是底乘高,乘起来面积肯定相等。
师:真聪明!能根据它们的面积计算公式很快看出它们的面积是相等的。你们行吗?人人都有机会。
教师分别出示平行四边形和三角形、三角形和梯形、梯形和平行四边形,引导学生比较出每组图形面积之间的关系,并说说想法。(学生回答略,逐步板书出图4)
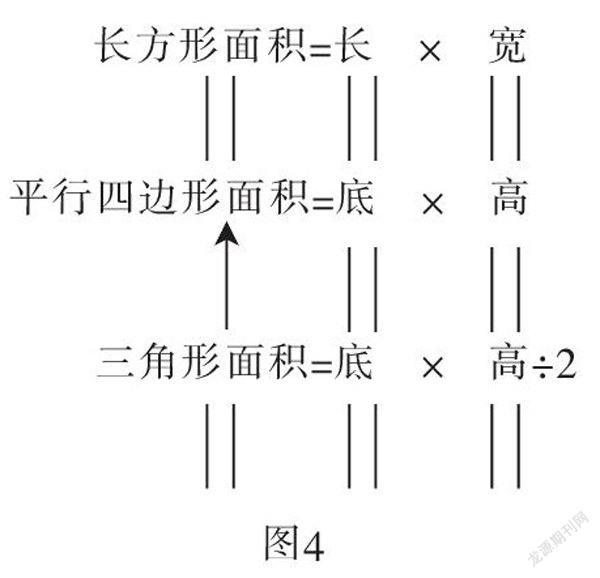
出示所有图形。提问:现在你能完整地说说它们面积之间的关系吗?和我们刚才的估计一样吗?
生:略。
比较四个多边形面积的关系,教师没有依赖行为操作或计算,而是注重引导学生通过符号化操作来实现,这一操作虽然不如行为操作或表象操作那样直观,但对于一单元结束后的复习课来说,学生在此之前已经积累了较为丰富的图形表象和相关知识储备。通过这一层次的操作活动,学生对多边形面积计算公式有了更深的理解和记忆,积累了丰富的数学活动经验,促使了学生在抽象能力、推理能力、操作能力、空间观念等多方面得到发展和提升。
三、经历反思的过程,提升、丰富数学活动经验
数学活动经验的积累不是一蹴而就的,是一个循序渐进、不断提升的过程。在课堂教学中,教师要注重引导学生经历积极思考、动手实践、自主探索等活动过程,通过这些方式获取丰富的直接经验,还要善于引导学生“反思过程”,反思自己是怎样发现问题、提出问题、分析问题并解决问题的;反思自己运用了哪些策略、方法;反思自己经历过的活动,看看有哪些收获及新的思考……通过反思,能让学生在活动中获得的经验得以提升,同时,反思本身就是活动过程的一部分,通过经历“反思”过程,能让学生数学学习的直接经验得以丰富和拓展。
【案例3】《用“数对”确定位置》
(简略描述之前的活动环节)
1.组织活动,“画”直角坐标
组织活动:先请这一横排的同学起立(班级座位的第一行),后面同学向前看齐。请这一横排同学从左往右依次报数,报完在纸上记下你报的数,后面同学在纸上帮你正前方的同学记下所报的数字。
2.在已有知识经验的基础上确定平面内一点的位置
指名一名学生,引导学生用诸如第几排第几个、第几组第几个等已有方式描述其位置。
3.用第几列第几行确定班级中的座位
结合教室座位介绍“第几列第几行”的描述规则,再将教室座位抽象为圆点图,引导学生在图中确定第几列和第几行,并介绍用“第几列第几行”确定位置的方法和规则。
4.用数对确定位置
引导学生自主尝试用最简洁、最精确的方式表示“第几列第几行”,并在交流的过程中引导学生注意数对中两数的顺序不可颠倒,再介绍“数对”的写法及表示的意义。
引导学生用数对表示班内多人及自己在教室中所在座位之后小结。
师:同学们,刚才我们已经学会了用第几列第几行确定自己的位置,并能更简洁地用一组数对来表示。其实回头看看,对照一下用数对表示的自己的位置和我们课堂开始时记下的两个数,你发现了什么?
生:我发现数对中的两个数就是我们在一开始记录下的两个数。
师:是的!其实,刚才我们在不经意间就创造出了数对的雏形,所以说,数学有时就这么简单,数对就是那样产生的!那我们再一起回顾一下你写那两个数的过程,说说我们如何用数对确定你的位置。
生:略。
课堂中学生不仅在操作中理解了“列”和“行”的概念,能用“第几列第几行”确定平面上的位置,还经历了自主“符号化”的过程,积累了数学活动经验。虽然多数学生都在尝试中出现了诸多问题,但这一过程的经历及其后教师的引导,让学生收获到知识层面的内容是对数对结构和特点的深刻、理性认识,而更重要的是在人心智的其他方面得到启迪与唤醒,感悟了数学的思想方法,体验到数学学习的乐趣,享受创造的喜悦。之后,教师引导学生经历反思的过程,学生回头再看前面经历的过程和积累的经验,感受到数学的产生并不神秘,而是在实际生活中对客观现象的抽象。在此过程中更深地感受到数学的简洁、准确及与生活的密切联系,并对自己尝试创造数对这一活动中获得的直接经验予以提升,为今后有效进行“符号化”的活动积累了科学的经验。

