让数学灵动起来
颜荣林 田海琪
【摘 要】“九宫图”是一个简易的数学模型,却蕴含着大量的数学规律。教师要想在探究“九宫图”的各种内在数学规律的基础上,充分开发“九宫图”的教育价值,就要对九宫图的文化背景、九宫图的不同填法、“九宫图”的数字规律等进行深入的分析,从而提出教学设想。
【关键词】九宫图 教学价值
“越是简单的知识,越能体现数学的本源。”九宫图就是这样的一个例子。在3×3的九个方格中,分别填入1至9这九个数。这是一个十分简单的数学问题,简单到只要以“20以内的加法”作为基础,就可以解决这个数学问题(如右图)。但是,却赋予它神话的色彩,下面让我们慢慢走进“九宫图”的世界。
一、九宫图的文化背景分析
相传,在夏禹时代,洛水中曾出现过一只大的神龟,它的背壳上有个图(如左下图),人们把这个图称作“洛书”。据说,这个图中蕴含了世间万物的变化规律, “洛书”为当时的首领大禹所得,他从中悟出了治理天下的道理。
“洛书”比较形象的称法是“九宫图”或“纵横图”,它的神奇特点吸引了无数人对它痴迷。从我国古代的“河出图,洛出书,圣人则之”的传说起,系统研究九宫图的第一人,是我国古代数学家——杨辉。

在国外,公元1300年被希腊数学家莫斯切普罗所推广,成为许多数学家倾注精力进行研究的一个数学题材。
九宫图中的原理连小学生都很容易理解,但它的内涵却是十分丰富的,它通过数字间的周转变化,数与形的和谐统一,局部与整体的全息对应,描绘出一个生动的宇宙演化的数学模型。它蕴含着大量的数学规律,“线线诸数合幻和、纵横巧合联四方、和差积方都巧等、三角方圆均有律”,它与算术、数论、幻方、代数几何、矩阵、趣味数学等都有联系。古今中外,不知多少学者著书立说,对九宫图进行深入的探索。
从上面的阐述中,感受到了“九宫图”所特有的文化内涵,从它“现世”的那一刻起,就注定成为一个融数理与神话为一体的数理哲学的化身。因此,在引入“九宫图”时,如果我们能创设情境,恰当地阐述“九宫图”的文化背景,可以激发学生对“九宫图”进行深入研究的兴趣。为后面研究或了解“九宫图”的各种不同的填法积累情感的基础。

二、九宫图的填写方法分析
九宫图的填法,如果用算术法凑数,可以用“罗列数组,对号入座”的方法很快地填出。但是,人们在此基础上,还创造出了许多口诀,根据口诀,可以按部就班地填出九宫图,增强填写“九宫图”的趣味性。下面我们列举几种适合小学生填写与了解的方法,并简要说明大致的教学设想。
(一)罗列数组,对号入座
这是最常用的构造九宫图的方法。
我们知道,把1至9这九个数填入“九宫图”,由于9个数的总和为45,每横行、每竖列、每横行和每斜行的三个数的和均相等,所以这样的每三个数的和都应该是15,也就是说从1至9中选出三个数,至少需要组成8组不完全相同的和为15的数组。经过试验有且只有8组,分别是(1,5,9,)(2,5,8)(3,5,7)(4,5,6)(2,4,9)(2,6,7)(3,4,8) (1,6,8)。
再观察右边的九宫图,写出以上8组和时,中间e的位置上的数被用到了4次,角上a,c,g,i的位置上的数被用到了3次,而边上b,d,f,h的位置上的数只被用到了2次。
按上面的规律,把8组数中各个数出现的次数做一个统计,可以发现“5”被用了4次,“2,4,6,8”各被用了3次,“1,3,5,7”各被用了2次。经过试验自然就可以把各个数“对号入座”了。
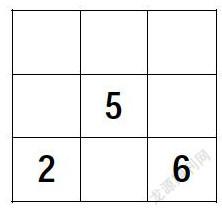
从上面的叙述中,可以设想到,如果只给出要求,学生按要求把1至9这九个数填入九个方格中,学生首先会进行尝试,当出现错误时,会不断地调整,这是最原始的尝试法。之后,再引导学生反思填写要求,逐步发现上面叙述的有序的填写思路。这就是数学思考的力量。这样的一个过程适合三年级时组织学生填写。而对于一、二年级的学生则可以先填其中部分数,让学生根据规则,填写出满足要求的其他位置上的数。如请补全右面的“九宫图”。

(二)归纳口诀,记忆填数
用上面的填法,固然可以填写九宫图,但是需要一个较长的过程。因此,还可以编写出填写的口诀。这些口诀又可以分为两类,一类是直接填数法,一类是表述过程法。
1.直接填数法

直接填数法就是依据口诀,可以依次直接填写出各个位置上的数。最有名的是:
戴九履一,左三右七,二四为肩,六八是足。
上面的口诀,分明就是一只乌龟的造型,如右图。
下面的口诀则是根据奇数与偶数不同位置特点编写而成的。
九数从小排到大,中间数字中间填,四角填上偶数项,余下四数再补全。
根据上面的口诀,可以按如下的图示填写。

这给我们提供了很好的教学思路:在学生按“罗列数组,对号入座”的方法填写出“九宫图”后,请学生阅读上面的两句口诀,说一说这两句口诀的意思及编写的思路。然后请学生再独立找一找“九宫图”中各个数的其他特征,自己来创作一句填数口诀。
2.表述过程法
用直接填数的口诀虽然形象生动,但是如果把它作为真正的填数方法,可能要增加学生的记忆负担。所以人们又创作出了另一种口诀,描述的是如何从最简单的数的排列,通过最简便的数的位置移动,实现填写九宫图的目的。
下面介绍的就是杨辉创造的一种填数口诀:
九数斜排,上下对易,左右互换。
读完上面的口诀,再看下面的两个图示,是否学会了“九宫图”的快速填法了?
在国外也有类似的口诀, “罗伯”口诀是其中有名的。
一填首行正中央,依次斜上莫要忘,
上出下填右出左,若是重了填下方。

右边的图示反映了按上面的口诀填数的过程。
根据口诀,只要找到“1”的位置,然后按规则从小到大填入其余各数的位置。
上面的这些填法,如何成为教学资源?我们设计了两种方案。
第一种方案是逐步渗透法。在一年级的教学中,根据学生的计算能力,做一些填数游戏,二年级再请学生按“罗列数组,对号入座”的方法填数,到了三年级,再请学生欣赏与研究口诀填数。
第二种方案是主题教学法。在三年级或者四年级时,组织一堂数学活动课,把以上一、二、三年级的教学内容串联成一堂活动课,让学生整体感受“九宫图”填写的内在魅力。
三、九宫图的内在规律分析

从上面的填写法的分析中,我们感受到了数学家对于“九宫图”的喜欢,他们不满足于常规的填法,创造出了许多口诀,体现了数学家的创造精神。但是,“九宫图”真正吸引人们,尤其是数学家的研究兴趣的,并不仅仅是它的数学文化背景或它的填法创造,更为重要的是“九宫图”——这个只有9个数构建而成的数学模型中所蕴含着的数学规律。笔者收集了其中一些浅显易懂的规律,力图让它们成为教学资源。
(一)“田—口=15”
“九宫图”中的任何一个“田”格中的4数之和,减去与此“田”格不同行不同列的另一格之数,必等于15。如(2+9+7+5)-8=15,(7+5+6+1)-4=15。
(二)相等数对
把“九宫图”的中心格5抹去(如左图)以后,经过中心格的任一条线上的两数和均是10。其实这种相等的数对处处可见:我们随意压住“九宫图”中的一格,那么与这格相交的各线,所剩的两数的和全相等。就如我们提起一个正方形网片一样,无论我们从哪个角上提起,从这个角向三个方向看去,所看到每条线上的两数之和都相等。
(三)递增和
“九宫图”中对称的两行或两列,将每行(列)各数依次乘一个等差数列的各项,各项积之和必相等。例如
2×1+9×2+4×3=6×1+1×2+8×3=32。
2×5+9×8+4×11=6×5+1×8+8×11=126。
4×11+3×21+8×31=2×11+7×21+6×31=355。
(四)平方和相等性
“九宫图”的第一、三行或者第一、三列所含的数的平方和相等,即42+92+22=82+12+62=101,42+32+82=22+72+62=89。
此外过中心4线上各数的平方和也有规律,请看:(22+52+82)+(42+52+62)+10=(72+52+32)+(92+52+12)-10=180。
(五)循环积和
“九宫图”中第一、三行或第一、三列,顺次两数相乘,其和必相等,即
2×9+9×4+4×2=6×1+1×8+6×8。
4×3+3×8+8×4=2×7+7×6+6×2。
(六)对称积和
在对称的两行或两列中,一条线上,两端两数之积的2倍,与中间一数的平方之和相等,例如
(2×4)×2+92=(6×8)×2+12=97。
(6×2)×2+72=(8×4)×2+32=73。
以上只是笔者收集到的关于“九宫图”规律的一小部分。显然,要把它们转化成课程资源,需要教师进行创造性的开发。
首先,把这些规律按发现的难度进行分类。如上面的六个规律,由易到难,最简单的是“相等数对”的规律,最难的当数“对称积和”。
对于这些规律,在教师的引导下进行自主发现。在这个过程中,如果学生有其他的新发现,同样给予肯定。如要求学生找“相等数对”时,有一位学生说,他还发现了“角上的数是相对的两个肩上数的和的一半”,并举例子:8=(7+9)÷2。同时,在找到“相等数对”后,教师也可以进一步追问与引导,让学生从中发现新的规律,如可以从“相等数对”中衍生出:角上四个数的和等于边上四个数的和。
其次,把这些规律按与教材知识的匹配程度分,具体安排在各个不同的年级,引导学生有不同的发现。
如在学习了多位数加法之后,教师请学生按下面的要求计算:计算顺写的三个三位数的和与逆写的三个三位数的和,进而总结出:顺写的三个三位数的和等于逆写的三个三位数的和。如 816+357+492=618+753+294。
进而追问:为什么会有这样的规律?知道了为什么后,再请学生计算竖着的顺写与逆写的情况下三个数的和是否相等。
上面的活动,利用学生新近学习的计算方法来探究“九宫图”中的新规律。既有利于提高学生的计算技能,同时又丰富了对“九宫图”规律的新认识,激发了学生的学习兴趣。
总之,对作为教学资源的“九宫图”规律的探究,并不是只为了探究规律而组织活动,它完全可以融合到我们平时的计算教学中,为计算教学平添了一道人文风景。
(浙江省杭州市萧山区所前二小 311200浙江省杭州市萧山区北干小学 311200)

