基于两级拓扑优化的振动台扩展台面设计与试验验证

刘 磊，马爱军*， 董 睿，刘洪英，石 蒙，冯雪梅，赵亚雄（中国航天员科研训练中心，北京 100094）

基于两级拓扑优化的振动台扩展台面设计与试验验证

刘 磊，马爱军*， 董 睿，刘洪英，石 蒙，冯雪梅，赵亚雄
（中国航天员科研训练中心，北京 100094）

根据拓扑优化基本原理，利用OptiStruct进行振动台扩展台面的结构最优化设计，通过两级拓扑优化完成结构的拓扑寻优。首先利用整体级拓扑优化，找到结构的整体最佳构造。然后利用局部级拓扑优化，对局部结构进行拓扑寻优，最终完成产品的结构设计。试验结果与仿真结果对比表明，误差在5 %以内，表明方法的有效性和实用性。

振动台扩展台面；拓扑优化；OptiStruct；结构设计；试验验证

前言

随着我国载人航天的蓬勃发展，越来越多的航天产品需要自主研发与设计。火箭在发射过程中要经历复杂的振动环境，据报道，40 %的航天事故是由振动引起的[1]，因而在航天产品研制过程中振动是重要的考虑因素[2]。为了验证产品的动力学特性是否满足要求，一般通过地面试验模拟发射过程中的振动环境[3]，即进行地面振动试验。

在进行振动试验时，产品一般通过夹具安装在振动台面上，由于振动台动圈台面尺寸有限，且与夹具的连接是固定位置的连接螺栓，因此尺寸和安装位置都受限。振动台扩展台面是进行振动试验时的通用夹具，使用扩展台面，可扩展原振动台动圈台面尺寸，扩展台面上的“米”字型安装槽增加了安装位置的灵活性。扩展台面的设计有以下两方面考虑：第一是基频足够大，尽可能远离产品试验频率；第二是质量尽可能轻，振动台的推力一定，运动部件越轻，就可以获得越大的加速度。

结构基频与质量存在着相互制约的关系，如何在满足基频要求的情况下，设计最轻的振动台扩展台面，是本设计追求的目标。传统手段依据经验进行的结构设计具有盲目性，得到的方案往往仅是可行方案，并非最优。本文选择利用拓扑优化技术[4-5]，通过计算机数值迭代以寻找结构的最佳传力路径，进行振动台扩展台面结构构造形式的最优化设计。

1 拓扑优化的原理

结构拓扑优化的基本思想是将寻求结构的最优拓扑问题转化为在给定的设计区域内寻求材料最优分布的问题，通过拓扑优化分析，设计人员可以全面了解产品结构和功能特征，可以有针对总体结构和具体结构进行设计[6]，结构拓扑优化示意图如图1所示。拓扑优化可以应用于结构设计的概念设计阶段，利用拓扑优化进行结构的最优化设计可以有效的避免依据经验进行结构设计的盲目性[7]。

目前常用的拓扑优化求解方法包括均匀化方法，变密度法，水平集法，ICM法，渐进结构法[8-9]。其中以变密度法应用最为广泛，优化软件OptiStruct，内部集成拓扑优化采用变密度法[10]。其中以质量最小为目标，以某阶自然频率为约束的拓扑优化可以表示为式（1）。

为了使拓扑优化结果更清晰的材料孔洞结构，对设计变量进行幂指数形式的惩罚，若采用SIMP插值函数，惩罚后结构整体质量和刚度矩阵为

其中M、K分别是质量阵、刚度阵。一般惩罚因子取值为q=1，p=3。

而结构的自振的有限元方程为

利用式（2）、（3）、（4）推导可得其第j阶本征值的灵敏度方程为

而质量与设计变量之间为简单的线性关系，灵敏度易求得。然后选择合适的迭代算法，比如移动渐近线法，即可进行结构的拓扑寻优。目前大型有限元软件包括NASTRAN，ANSYS，OptiStruct等都包含拓扑优化模块，本文主要利用OptiStruct对振动台扩展台面进行拓扑最优化设计。

2 振动台扩展台面的设计

2.1 问题描述

振动台扩展台面要求台面尺寸1 000 mm * 1 000 mm * 40 mm，通过底部32个安装孔与动圈相连，安装孔位置固定。安装孔直径26 mm，出于制造方面考虑，设置安装孔附近最低厚度40 mm。因此可以定义其非设计区域为如图2（a）所示。为了寻找结构的最佳承载方式，将其余部分设定为设计域，以对整体结构进行拓扑寻优，寻找最需要材料的地方，如图2（b）。

为了对结构整体情况做初步了解，分别对图2（a）非设计域和图2（b）整体结构进行有限元建模，然后分别进行模态分析，表1为两种结构的质量与基频。其中非设计域基频仅为307 Hz，远小于目标值850 Hz，故有必要对设计域进行结构整体拓扑寻优。

图1 结构拓扑优化示意图

图2 振动台扩展台面非设计域与整体结构

2.2 一级拓扑优化：整体级拓扑寻优

利用OptiStruct进行结构的拓扑优化，约束设定基频最小为850 Hz，目标为质量最小。为保证满足制造要求，分别设置最小尺寸约束20 mm和两个对称约束。经过65次迭代结果收敛。图3分别为保留相对密度值为0.8、0.6、0.4、0.2时的结构构造形式。

由图3可知，整体拓扑寻优结果表明，材料密度最大的位置为非设计域八个尖端延伸位置处，因此在八个尖端延伸处添加材料。其次，材料密度较大处为连接尖端的位置，但材料具体如何布置最为合理仍不清晰，因此需要进行二级局部拓扑寻优，将连接尖端的位置重新设定为设计域，寻找局部结构材料的最佳布置，如图4所示。二级拓扑优化中，当设计域为0时，可简化为图3（a）模型，此时结构基频为822 Hz，仍小于目标值850 Hz。而随着设计域材料的增加，同样可简化为图3其他几个模型。

2.3 二级拓扑优化：局部级拓扑寻优

在局部级拓扑优化中，同样利用OptiStruct进行迭代以寻找局部结构材料的最优分布，以使细节部位的结构布局更加合理。经过13轮迭代，结果收敛，得到最终拓扑优化结果如图5所示，其中取iµ>0.5。

表1 非设计域与整体结构的质量与基频

图3 一级拓扑优化结果

2.4 最终模型与产品实物

二级拓扑优化结果显示，可以对图4设计域中间进行挖孔操作，而圆孔尺寸可以根据加工制造要求进行合理设计，最终振动台扩展台面设计模型如图6（a）所示，对最终模型进行模态分析可以得到结构的基频为881 Hz，满足目标要求。根据最终模型图加工制造得到振动台扩展台面实际产品如图6（b）所示。

3 实验验证

对振动台扩展台面产品进行振动实验，以测试其实际固有频率。其振动试验及驱动曲线如图7所示。由驱动曲线图可知结构基频为900 Hz，仿真结果与实测结果数据如表2所示。

结果表明，通过试验与仿真得到的质量与基频虽存在一定误差，但都在5 %以内。下面对误差进行分析：对于质量误差，主要为加工制造过程带来的误差以及实验测量误差。而对于频率误差，有限元建模过程的误差，其中主要是螺栓连接的处理方式，会直接影响结构的基频，另外还存在实验测量误差等。

4 结论

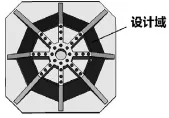
图4 局部结构拓扑寻优设计域

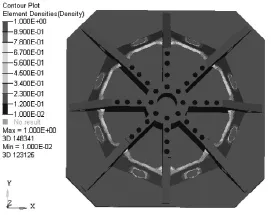
图5 二级拓扑优化结果

图6 振动台扩展台面最终模型与产品实物图

图7 振动台扩展台面振动试验及驱动曲线图

表2 实测结果与仿真结果的比较

1）传统手段依据经验进行的产品结构设计具有一定的盲目性，而通过拓扑寻优可以找到结构最佳的承载方式，避免材料的浪费。在结构整体设计以及局部设计中都可以拓扑优化进行结构寻优，通过多级拓扑优化会得到更为清晰的结构构造形式。

2）针对振动台扩展台面，利用OptiStruct通过整体与局部两级拓扑优化完成对振动台面的结构设计。试验结果与仿真结果对比表明，利用计算机进行结构拓扑寻优的有效性和实用性，可以为类似产品设计提供参考。

［1］ 顾松年， 徐斌， 荣见华， 等.结构动力学设计优化方法的新进展［J］.机械强度， 2005， 27（2）：156-162.

［2］ 马兴瑞， 于登云， 韩增尧， 等.星箭力学环境分析与试验技术研究进展［J］.宇航学报， 2006， 27（3）： 323-331.

［3］ 邱吉宝， 王建民， 谭志勇， 等.航天器结构动态优化设计仿真技术［J］.强度与环境， 2003， 30（2）： 6-16.

［4］ Bendsoe M P， Sigmund O.Topology optimization： theory，methods and applications ［M］.New York： Springer Press， 2003.

［5］ 邓扬晨， 陈华， 马明亮， 等.基于拓扑优化技术的飞机普通框设计方法研究［J］.强度与环境， 2005， 32（2）： 39-45.

［6］ Cheng G D.Introduction to structural optimization： theory，methods and solutions ［M］.Technical University of Denmark， 1992.

［7］ 郭永辉， 范新中， 路志峰， 等.基于结构拓扑优化的惯组基座轻量化设计［J］.强度与环境， 2010， 37（1）： 16-21.

［8］ 罗震， 陈立平， 黄玉盈， 等.连续体结构的拓扑优化设计［J］.力学进展， 2004， 34（4）： 463-476.

［9］ 郭中泽， 张卫红， 陈裕泽， 等.结构拓扑优化设计综述［J］.机械设计，2007， 24（8）： 1-6.

［10］ 张胜兰.基于HyperWorks的结构优化设计技术［M］.北京： 机械工业出版社， 2007.

Design of Vibration Expander Uniformity Based on Two-level Topology Optimization and Experimental Verification

LIU Lei， MA Ai-jun， DONG Rui， LIU Hong-ying， SHI Meng， FENG Xue-mei， ZHAO Ya-xiong
（China Astronaut Research and Training Center， Beijing 100094）

Based on the fundamental principles of topology optimization， the optimum design of expander vibration uniformity was finished by two-level topology optimization by using OptiStruct software.Firstly， the whole optimum structure was found by integral topology optimization， then local optimum structure was found by local topology optimization， and the final structure design could be achieved.The comparison of experimental results and simulation results showed that the error existed but was less than 5 %.It proved effectiveness and practicability of the method.

vibration expander uniformity； topology optimization； OptiStruct； structure design；experimental verification

TH122

A

1004-7204（2016）03-0005-05

中国载人航天工程基金项目资助

刘磊（1991-），男，硕士，研究方向：振动、冲击环境下结构优化设计。

马爱军（1969-），男，研究员，博士。研究方向：机械结构设计、振动冲击环境试验。