PSO算法在马斯京根法参数率定中的应用

李　匡，胡宇丰，梁犁丽，徐海卿

PSO算法在马斯京根法参数率定中的应用

李匡，胡宇丰，梁犁丽，徐海卿

（北京中水科水电科技开发有限公司，北京 100038）

将PSO算法用于马斯京根法参数的自动率定，开发了基于PSO算法的马斯京根法参数自动率定系统，该系统可以对马斯京根法参数进行快速的率定和检验；是分析率定结果稳定性的一种新方法；此系统具有较高的实用性，已在多个流域中得到了应用。

马斯京根法；参数率定；PSO算法；参数自动率定系统；数据稳定性

1　引言

马斯京根法是一种广泛应用于河道洪水流量演算的方法，是美国工程师G.T.Mccarthy于1938年提出的流量演算法，此法最早在美国马斯京根河流域上使用，因而称为马斯京根法。该法建立马斯京根槽蓄曲线，并与水量平衡方程联解，进行河段洪水演算[1]。该方法在实际应用中的一个重要问题是模型的参数估计。在传统方法中利用试算法对参数K、x进行率定，再计算出决策变量C0、C1、C2，但是试算法具有盲目性、不确定性、不易程序化且精度不高等缺陷[1-2]。因此有学者选择了直接优化决策变量C0、C1、C2，得到较好的效果，主要方法有最小二乘法[3]，遗传算法[4-5]，粒子群算法[6]等。

粒子群优化算法（ParticleSwarmOptimization Algorithm，PSO）是进化算法的一种，系统初始化为一组随机解，通过迭代搜寻最优值。传统PSO算法在应用中和其它全局优化算法一样可能会陷入局部最优，导致收敛精度不高，后期收敛速度较慢，经过学者的研究对粒子群算法进行了改进，使得粒子群算法的效率得到了较大的提高[7-8]。另外，同其它的进化算法，如遗传算法相比，PSO模型具有参数较少，原理简单，易于实现，计算效率高等优点。鉴于以上优点，本文选择PSO算法率定马斯京根法参数。

马斯京根法参数率定是一个非线性优化问题，利用PSO算法进行率定是合适的。在应用PSO算法进行马斯京根法参数率定时，需要给出马斯京根法各参数的取值范围，然而在已有的研究文献中，作者并没有明确给出各参数的取值范围。本文根据严格的数学证明给出了马斯京根法参数的取值范围，为广大学者在应用各类优化算法进行马斯京根法参数率定提供参考。

作者开发了基于PSO算法的马斯京根法参数自动率定系统，按照给定的数据库表结构输入资料（流量，断面信息），系统可以对流域中各河道的马斯京根法参数进行自动率定，并对率定出的马斯京根法参数进行检验。

2　马斯京根法简介

马斯京根法基本原理如下：对水量平衡方程（1）和马斯京根槽蓄方程（2）进行求解：

式中：I上断面的流量；I1，I2时段始末上断面的流量；Q下断面的流量；Q1，Q2时段始末下断面的流量；△t计算时段长；S河段蓄水量；S1，S2时段始末河段蓄水量；K稳定流情况下的河段洪水传播时间；x槽蓄系数。C0，C1，C2是 K，△t，x的函数，并且C0+C1+C2=1

3　粒子群（PSO）算法及其计算流程

PSO算法是Kennedy和Eberhart于1995年提出的一种基于对鸟群捕食行为模拟的智能群集优化算法。其基本思想可以简单地表述为：在一个优化问题的解空间中，每一个可行解被看做一个“粒子”，这些粒子在解空间内不停地飞行，在飞行的过程中根据自身和种群中其他粒子积累的经验不断调整自己的飞行策略，最终这些粒子都趋于解空间中的最优区域，也即所谓的“食物”[10]。

PSO算法的数学描述如下：在一个n维的搜索空间中，由m个粒子组成一个种群，即X={x1，x2，x3，…，xi，…xm}T，第i个粒子的位置为xi=（xi1，xi2，xi3，…，xin），其速度为Vi=（Vi1，Vi2，Vi3，…，Vin），粒子的个体极值为：Pi=（Pi1，Pi2，Pi3，…，Pin），种群的全局极值为：Pg=（Pg1，Pg2，Pg3，…，Pgn），基本PSO算法的粒子在搜索过程中通过式（3）和式（4）不断地进行位置和飞行速度的更新：

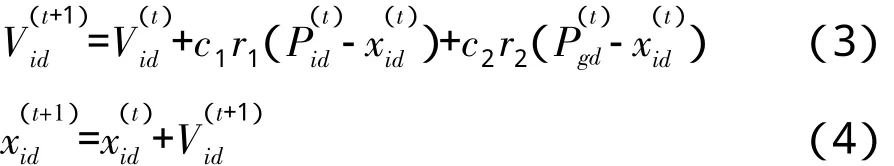
其中：d=1，2，3，…，n；i=1，2，3，…，m。

式中：n为粒子的维数；m为种群的规模；t为当前的迭代步数；r1，r2分别为0和1之间的随机数，c1，c2为加速度常数。

粒子的维数n与具体的研究问题有关，例如在率定马斯京根法参数时，有三个参数需要率定，则n=3。

种群规模m影响算法的稳定性和效率，m取值越大，PSO算法的稳定性越好，但同时计算量也较大，耗时长，计算效率较低。因此在对精度要求较高时可选择较大的种群规模，对计算效率要求较高时选择较小的种群规模，种群规模m的取值范围一般在[50，100]之间。

从式（3）可以看出，粒子飞行速度更新公式包括三部分：第一部分是粒子的历史飞行速度，说明了粒子目前的状态，起到平衡全局和局部搜索能力的作用；第二部分是粒子自身的认识，表示粒子在飞行过程中自身的思考；第三部分是粒子的社会认识，表示粒子群中各粒子之间信息的交流。三个部分共同作用，决定了粒子的空间搜索能力。

传统的粒子群算法容易陷入局部极小值，影响PSO算法找到全局最优值。为了提高PSO算法的优化性能，平衡算法的全局搜索能力和局部搜索能力，文献[11]对基本PSO算法进行了改进，在基本PSO算法的基础上引进了惯性权重项ω，提出了标准PSO算法。式（3）也相应地修正为：

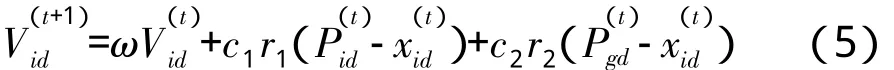
式中ω的取值方式有两种。一种是递减策略，惯性权重ω满足ω（t）=0.9-t×0.5，其中t为当前迭T 代次数，T为最大迭代次数；另外一种是固定策略，通常取惯性权重为[0.4，0.6]中的某一固定值。

根据PSO算法基本思想，可以设计标准PSO算法的流程如下：

（1）将优化的问题数学模型化，选定优化问题的目标函数（即适应度函数），选定粒子的维数；

（2）初始化算法。对粒子群中的粒子位置和速度进行初始化设定，即在一定的范围内随机产生出每一个粒子的位置和速度；

（3）根据优化问题的目标函数计算每个粒子的适应度值；

（4）对每个粒子，将其当前适应度值与其所经历的最优适应度值进行比较，如果该粒子的当前适应度值更优，那么将当前位置记录为该粒子的局部最优位置；

（5）对每个粒子所经历的最优适应度值与全局最优适应度值进行比较，如果个体粒子的最优适应度值较全局最优适应度值为优，则将其作为全局最优位置；

（6）对每个粒子的位置和飞行速度进行更新；

（7）判断是否达到优化的终止条件。如果满足终止条件，结束循环，否则返回第三步。

4　马斯京根法参数率定系统

本文利用Vb.net开发了马斯京根法参数率定系统，该系统利用PSO算法对马斯京根法参数进行率定。将各水文站的测站信息、流量资料等按照系统设计的数据库表结构输入到数据库中，系统即可按照默认设置的PSO算法参数对马斯京根法参数进行率定，并且可以对率定的参数进行检验及分析。

在用PSO算法进行马斯京根法参数率定时，还需要解决以下几个问题：

4.1目标函数

采用PSO算法率定模型参数时必须构建目标函数，一方面用以评价模拟效果的优劣，另一方面作为粒子飞行策略调整的标准。在对马斯京根法参数进行率定时，一般有河槽蓄量误差最小和流量误差最小两种目标函数，经学者研究表明，选用流量误差最小作为目标函数率定的马斯京根法参数效果更好[12]。

本系统将计算流量和实测流量的误差平方和最小作为判断马斯京根法参数寻优的目标函数：

式中：Qi为第i时段计算出流量，QiC为第i时段实测出流量，n为总时段数。

4.2参数率定结果的稳定性分析

在利用PSO算法率定马斯京根法参数时，由于PSO算法的初始解是随机给定的，因此可能会造成率定的参数不稳定。该问题可以通过多次计算，得到率定参数结果序列，然后检验参数结果序列是否稳定，如果稳定，则取参数结果的平均值作为最终率定参数结果；如果未通过稳定性检验，则调整PSO参数重新率定，直到率定的参数结果稳定为止。

可以通过以下算法检验率定的参数结果是否稳定：

该算法的核心是计算聚集在平均值附近的数值的概率，当该概率大于稳定指标时，则确定该数据序列是稳定的，反之数据不稳定。判断过程可按照以下步骤进行：

（1）分析数据的特点，确定合适的稳定性指标S以及稳定性判别变化幅度Adec；

（2）计算该段数据序列的平均值Vavg；

（3）给定变化幅度A（0≤A≤1）围绕平均值Vavg上、下波动，得到区间[Vavg-Vavg×A，Vavg+Vavg×A]，称此区间为稳定区域F。计算稳定区域内数据出现的概率P，即稳定区域内出现的数据个数与整个时间段内数据的总个数的比值。如果P大于稳定指标F并且abs（P-S）≥ε，则转至（4）继续；如果P小于稳定指标S并且abs（P-S）≥ε，则转至（5）继续；如果abs（P-S）≥ε，则转至（6）；

（4）减小变化幅度A，转至（3）重新计算；

（5）增大变化幅度A，转至（3）重新计算；

（6）如果A≤Adec，则认为数据序列稳定，否则认为数据序列不稳定。

此法的优点是：不仅可以判断数据是否稳定，而且可以判别出数据在多大的范围内稳定。

4.3有支流断面的参数率定问题

对有支流汇入的断面，系统中采用“先合后演”的方法进行参数率定，即将干、支流所有上断面相同时刻的流量相加，作为河段总入流，按无支流河段方法进行演算[2]。

4.4系统中PSO算法默认参数

（1）计算次数：ComputeCount=50；

（2）种群规模：m=70；

（3）粒子维数：n=70；

（5）限制条件C2=1-C0-C1，当C2超出其取值范围，则调整至其取值范围；

（6）加速因子：设定为C1=C2=2.0；

（7）惯性权重：从0.9～0.4递减变化或者取固定值ω=0.5，默认选择后一种；

（8）速度限制系数：k=0.7；

（9）终止条件：最大迭代次数T=200，或者目标函数之差小于给定精度ε=10-8。

表1　率定误差与检验误差比较

在实际应用中用户可以通过对以上参数进行修改，找出率定效果较好的马斯京根法参数。

5　实例

采用雅砻江流域上三个测站的资料进行马斯京根法参数率定和检验。三个测站的地理位置示意图如图1所示：

图1　测站地理位置示意图

将麦地龙站和列瓦站同时刻的资料相加作为入流量，将锦屏站的资料作为出流量。利用2006～2008年的资料进行参数率定，再利用2009年的资料进行检验，我们得到如下结果：

率定结果C0=0.056，C1=0.001，C2=0.942。

资料的率定误差和检验误差分别如表1。

先对每次计算所得的最优目标函数值序列以及参数序列分别进行归一化处理；再计算目标函数值的方差为0.1466，率定参数的方差分别为0.0396，0.0218，0.0849，证明PSO算法具有较高的稳定性。

每次计算当目标函数达到终止条件所需的平均迭代次数为27.66次，最大次数为54次，最小次数为13次，因此PSO算法也有较高的效率。

由于在参数率定时，选用的资料序列较长，计算量较大（因为计算50次需要的时间较长）。鉴于PSO算法的稳定性和效率，在实际应用中可以不用计算50次，只需计算5次左右即可，以期节省计算时间。另外，如果对精度要求不高，可以将终止条件中的目标函数之差设为ε=10-5，此举也可节省计算时间。

6　结束语

本文将PSO算法用于马斯京根法参数的自动率定中，开发了基于PSO算法的马斯京根法参数自动率定系统，此系统具有较高的实用价值，适合内嵌入洪水预报系统进行参数率定和检验；该系统在雅砻江流域和丰满流域等的洪水预报过程中均得到了应用，取得了较好的参数率定和检验效果。但是当率定参数采用的资料较长时，需要的时间也较长，下一步我们将再对PSO算法进行改进，以提高系统的运算效率。

[1]詹道江，叶守泽.工程水文学[M].北京:中国水利水电出版社，2000.

[2]包为民.水文预报[M].3版.北京:中国水利水电出版社，2006.

[3]翟国静.马斯京根模型参数估计方法探讨[J].水文，1997，3: 40-43.

[4]鲁帆，蒋云钟，王浩，等.多智能体遗传算法用于马斯京根模型参数估计[J].水利学报，2007，38（3）：289-294.

[5]董纯，康玲，侯国祥.基于遗传模拟退火法的马斯京根方程参数估计[J].华中科技大学学报（自然科学版），2002，30

（10）:20-22.

[6]李明明，李承军，张铭.改进PSO法在马斯京根模型参数估计中的应用[J].人民长江，2008，39（3）：60-62.

[7]李建勇.粒子群优化算法研究[D].杭州:浙江大学，2004.

[8]熊鹰.微粒群算法的若干改进及应用[D].武汉:武汉理工大学，2006.

[9]李匡，付力，胡宇丰，等.马斯京根法参数C0，C1，C2取值范围的确定[J].南水北调与水利科技，2012，10（5）:43-45.

[10]刘苏宁，甘泓，魏国孝.粒子群算法在新安江模型参数率定中的应用[J].水利学报，2010，41（5）:537-544.

[11]ShiY，EberhartRC．EmpiricalStudyofParticleSwarm Optimization[C]//Proceedingofthe1999CongressonEvolutionaryComputation．Piscataway，NJIEEEServiceCenter，1999．

[12]董晓华，刘冀，徐刚，等.目标函数对马斯京根法河道流量演算精度的影响[J].水文，2009，29（6）：9-13.

TV734

B

1672-5387（2016）08-0088-04

10.13599/j.cnki.11-5130.2016.08.027

2016-06-29

李匡（1983-），男，高级工程师，从事洪水预报调度系统开发工作。