A Noise Suppression Scheme with EEMD Based on Angle Cosine and Fuzzy Threshold*

MA Ziji，GUO Shuaifeng，LI Yanfu（School of Electrical and Information Engineering，Hunan University，Changsha 410082，China）



A Noise Suppression Scheme with EEMD Based on Angle Cosine and Fuzzy Threshold*

MA Ziji*，GUO Shuaifeng，LI Yanfu
（School of Electrical and Information Engineering，Hunan University，Changsha 410082，China）

In this paper，a novel noise suppression scheme that exploits the angle cosine and fuzzy threshold，is pro⁃posed to improve the denoising accuracy for nonlinear and non-stationary signals.The proposed scheme combines with the adaptive characteristics of the conventional EEMD as well.Firstly，the similarity between intrinsic mode function（IMF）and observed signal is calculated by the angle cosine method.The IMFs are then divided into noise dominated and signal dominated part by finding the latter location of the first minimal value of cosine similarity curve.The VisuShrink threshold tends to“overkill”the detail coefficient，while the SUREShrink threshold tends to“underkill”the noise coefficient.Employing a fuzzy threshold that is an optimal value within the convergent range of VisuShrink and SUREShrink threshold，we can remove the noise part from the noise dominated IMF well.Finally，all of the remained IMFs are reconstructed to get a noise suppressed signal.Simulation experiments are conducted by us⁃ing both suppositional and actual ECG signal.The simulation results demonstrate that the proposed scheme can effec⁃tively suppress the noise，and has better denoising performance than some conventional schemes，such as the half soft threshold wavelet method，EMD soft threshold（EMD-soft）method and the EMD interval threshold（EMD-IT）method.

signal denoising；ensemble empirical mode decomposition；intrinsic mode function；angle cosine；fuzzy threshold

在仪器仪表和测量领域，信号去噪是一个经典的问题，良好的去噪方法可以降低由于信号的不确定性而造成的去噪效果的差异。由于实际信号大多是非平稳信号，所以传统的分析方法，例如基于维纳滤波的消噪方法已不能满足要求。小波分析由于良好的时频分析特性解决了分析非平稳信号的问题，但是用小波变换进行去噪时需要预先设定小波基和分解层数。研究表明［1］，选用不同的小波基和分解层数对信号的去噪效果影响很大。聚合经验模态分解EEMD（Ensemble Empirical Mode De⁃composition）是一种新的数据分析方法［2］，它无需设定基函数，完全根据信号本身的特征进行分解，将其从高频到低频分解成具有物理意义的几个本征模态函数IMF（Intrinsic Mode Function）和一个余量，适用于非平稳信号的分析。同时也避免了信号经过经验模态分解［3］EMD（Empirical Mode Decomposi⁃tion）过程中可能出现的模态混叠现象，所分解出的IMF更好的反映了信号的特征，去噪性能更具有自适应性，已经被广泛的用于各种领域。

然而EEMD也存在着如何有效的选取模态的问题。文献［4］已经证明信号的重要成分主要集中在含噪低的高阶IMF分量中，即信号主导模态；而在含噪高的低阶IMF分量即噪声主导模态中分布较少。文献［5］提出利用噪声自相关特性并对方差设定合适的阈值，克服了文献［4，6-7］依据连续均方误差法和相关系数法容易受信噪比变化影响的缺点，较好地确定了噪声主导和信号主导分界的IMF分量，但是阈值的确定并没有给出准确的准则。另外仅利用信号主导IMF的局部重构法在去噪的同时会不可避免地丢失一部分有用信号，尤其当信噪比较高的时候更为明显。在文献［5］中将噪声主导IMF使用小波变换法去噪，消噪性能缺乏自适应性。文献［8］中提出将指定的几层IMF经过间隔阈值法处理，然而参数M1和M2以及阈值的确定缺乏足够的理论支撑。

针对以上问题，利用EEMD的抗模态混叠的优点，本文提出一种基于夹角余弦和模糊阈值的去噪方法。利用夹角余弦法计算经EEMD分解得到地IMF与观测信号的相似度得到信号主导模态与噪声主导模态分界的IMF，分层效果更具有鲁棒性；并在噪声主导模态中引入模糊区域，通过隶属度函数对模糊区域内的系数进行缩减，然后将所有的IMF合并得到消噪信号。实验表明，该方法可以在有效消除噪声的同时，较好地保留了信号的细节。

1　EEMD算法

针对EMD分解中的模态混叠现象，Wu等人提出了EEMD方法。该方法是利用高斯白噪声具有频率均匀分布的统计特性。当向信号中加入高斯白噪声后，信号将在不同尺度上具有连续性，保证了每次对信号都能够准确求得上下包络的局部均值，避免了EMD分解的模态混叠现象。

EEMD具体分解过程如下：

在目标数据x（t）上加入白噪声序列n（t），且白噪声序列均值为零、方差为常数，得到一个总体序列X（t），即：

将加入白噪声的信号序列X（t）利用EMD方法分解为一组本征模态函数IMF和残余分量rc（t），可以表示为：

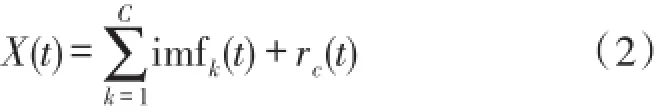
每次加入不同的白噪声，重复上述过程，得到：

把m次分解得到的各个IMF分量求取均值作为目标信号的最终分解结果，

2　基于夹角余弦和模糊阈值的EEMD的去噪方法

2.1夹角余弦法分离噪声主导模态

为了得到噪声主导和信号主导分界的位置Kth，本文采用相似度方法。可以认为信号主导模态与原始信号具有较多的相似特征，而噪声主导模态与输入信号的相似性较少。本文利用夹角余弦方法计算观测信号和每一个IMF的相似程度。假定两个数据序列之间的夹角是处于0到90°的闭区间内，当夹角趋于90°时两个时间序列最不相似，此时的余弦值最小。当夹角趋于0°时两个时间序列最相似，此时的余弦值最大。在机器学习中，余弦相似度（Cosine Similarity）是一种有效的证明数据序列之间相似性的方法。令x和y为N维的列向量，则它的公式可以表示为：

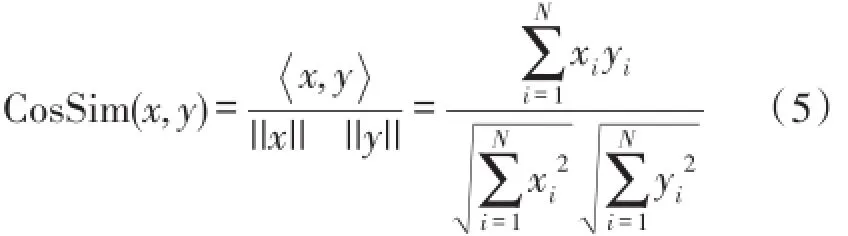
将含噪信号x（t）和imfk（k=1，2...C）之间的相似性定义为：

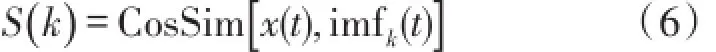
确定Kth的原则是寻找相似度首次发生开始逆向转折的位置，可以认为此时Kth是处于IMF分量与原始信号之间的相似度由逐渐减小转换为逐渐变大的分界点。所以本文将Kth定位在S（k）的首个极小值的后一个位置。如一个仿真信号y（t），添加高斯白噪声n（t），当含噪信号信噪比SNR（Signal To Noise Ratio）为5 dB时可表示为：x（t）=y（t）+n（t）。任意的，令y（t）=cos（2πf1t）+sin（2πf2t），其中f1=0.8 Hz，f2=2Hz。采样频率为0.1 kHz，采样长度为2 048。将噪声标准差设为0.4，添加噪声次数为20。经过EEMD分解之后，它的各个IMF分量及其与含噪信号之间的余弦相似度关系曲线S（k）分别如图1和图2所示。图1可以看出对该仿真信号来说从IMF分量的第四层开始噪声部分明显减少。图2可知经本文提出地确定Kth的原则也是自动确定了Kth= 4，表示imf4～imf11为信号主导的IMF分量，imf1～imf3为噪声主导的IMF分量。同时也可以看出在与观测信号相似性最高IMF之后相似性会出现下降的情况，这是因为在高阶IMF分量中信号的幅度较小，更多体现的是信号的趋势部分。

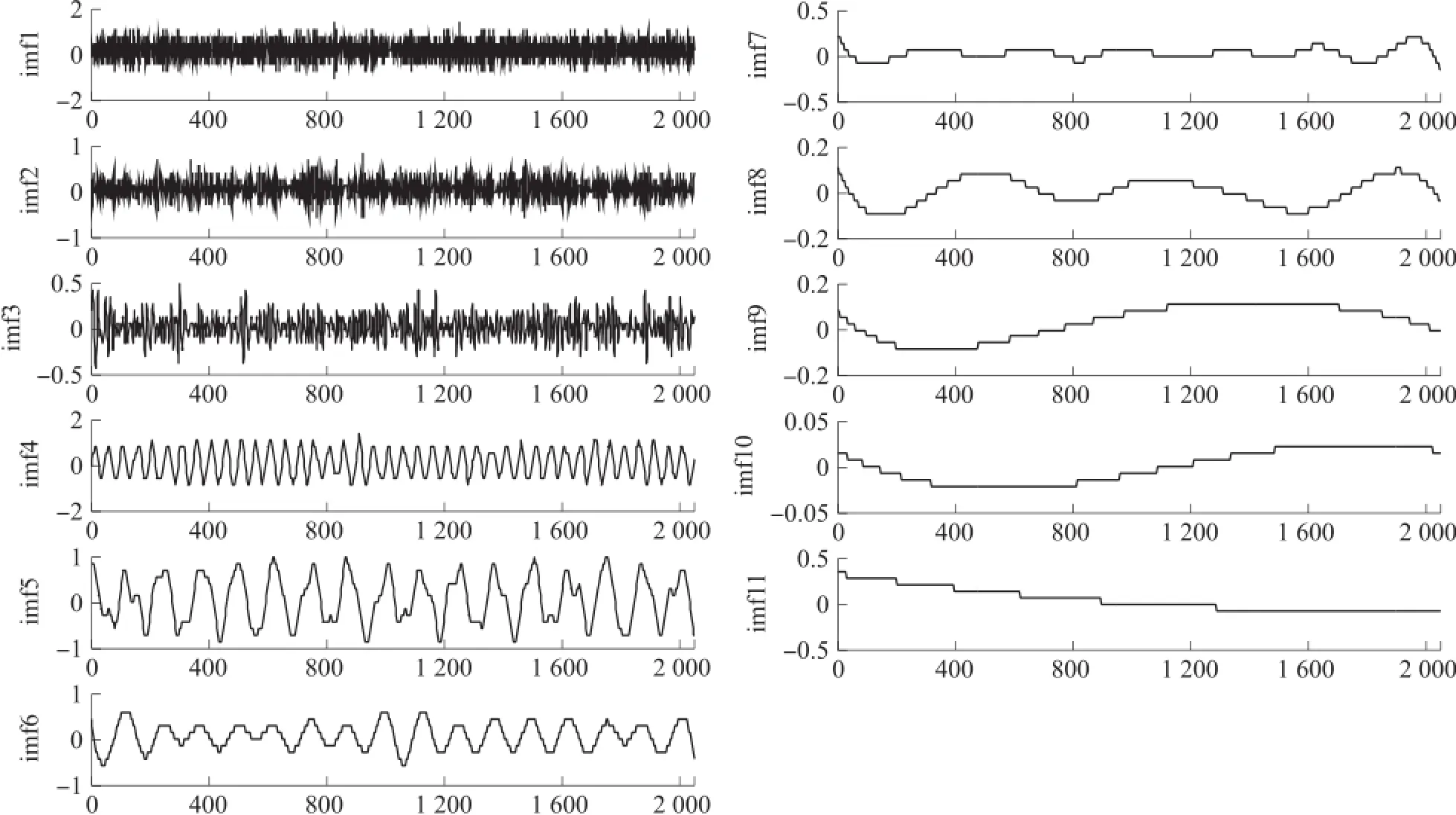
图1　含噪声的测试信号EEMD分解结果

为了进一步确认该方法确定Kth的有效性，从第二层IMF开始以逐层递增方式合并后边几层IMF分量，得到初步的消噪信号如如图3所示。并与原始信号对比，分别计算其信噪比SNR和均方根误差RMSE（Root Mean Square Error），结果表1所示。

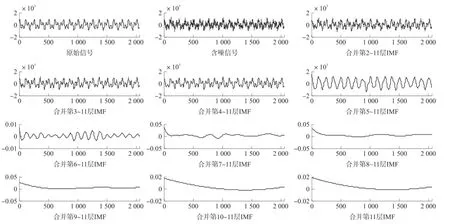
图3　原始信号依次合并后几层的IMF分量

表1　依次合并后几层IMF分量的去噪效果比较

由图3可看出，当合并第4～11层IMF分量时，输出信号在保持信号细节的同时噪声成分明显较少，而且表1中也可以看出此时得到的消噪信号的SNR最大，RMSE最小，此时的信号最接近原始信号y（t），表明使用本文提出的夹角余弦法可以精准的寻找到信号主导IMF和噪声主导IMF的分界位置，确定Kth的值。

2.2模糊阈值处理

阈值消噪方法是目前应用最为广泛和有效的一种方法。其步骤如下：首先将信号分解成多个IMF分量，并选取合适的阈值λk对imfk中的系数进行阈值处理；然后将所有的IMF分量合并即可得到消噪信号。阈值的确定有很多种方法，其中包括：

①VisuShrink阈值，也称为通用阈值，是一种多尺度的统一阈值去噪方法。这种阈值是针对多维独立正态变量联合分布，在维数趋近于无穷时得出的结论，即大于该阈值的系数含有噪声的概率趋近于零［9］，以实现去噪的目的，因此当N变大时容易出现阈值设定过大的问题。对分解出来的每一层信号设定一个阈值，其中当信号长度为N时第k层的阈值可以表示为：

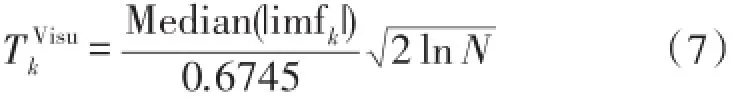
其中，Median表示取中值操作。

②SUREShrink阈值，这种阈值选择方法是一种基于史坦的无偏似然估计（Stein’s Unbiased Estimator of Risk，简记为SURE）准则的自适应阈值选择。该准则是均方差准则的无偏估计，它是专门针对软阈值函数得出的结论，且SUREShrink阈值趋近于理想阈值。与多尺度统一阈值相比，能够更好地保持信号的细节，但是这种阈值选取方法容易过多地保留信号的细节部分，在信噪比提高方面不占优势。在EEMD分解的第k层上，SUREShrink按照如下公式选择阈值：

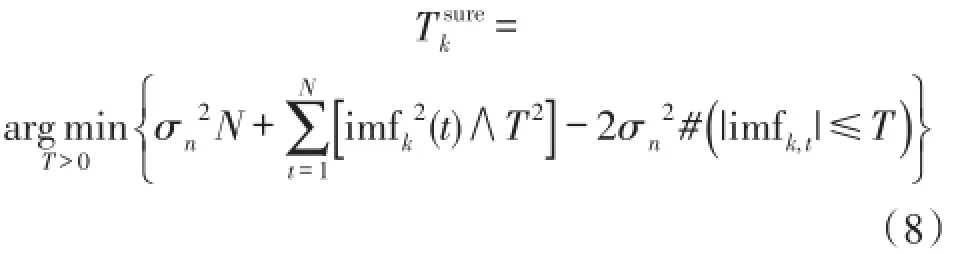
其中，T∈｛0，max［imfk（t）］｝，N为信号的长度，imfk，t表示第k层imf的第t个系数，∧表示两数取小运算，#（|imfk，t|≤T）表示第k层中系数小于T的个数，σn为噪声的标准差，利用EEMD分解之后的第一层IMF分量由经典的Donoho公式得到，可以表示为［10］：

针对VisuShrink阈值的“过扼杀”和SURE⁃Shrink阈值的“过保留”的特点［11］，本文将Shark提出的模糊阈值思想［12］用于噪声主导的IMF分量去噪处理。摒弃了传统方法中固定阈值的方法，而是通过设定一个模糊区域和隶属度函数，将该区域的上界和下界设定为VisuShrink阈值和SUREShrink阈值。将绝对值|imfk，t|大于VisuShrink阈值的系数视为是由信号引起的，小于SUREShrink阈值的系数视为噪声引起，位于模糊区域的系数使用隶属度函数μk（imfk）进行萎缩。考虑到此处的模糊函数是用于噪声主导模态的处理，系数分布满足偏大型的模糊分布，萎缩后的系数及偏大型模糊分布的一般形式如下所示：

其中，a为常数，是模糊隶属度函数曲线与横轴的交点到坐标原点的距离，表示模糊区域的下界SUREShrink阈值；f（imfk，t）为函数值小于1的曲线，可以通过改变它的形式得到不同的偏大型的模糊分布函数，其中包括：梯形，抛物型和正态型等，如图4所示。图中b表示模糊区域的上界VisuSh⁃rink阈值。

因为是对噪声主导模态进行处理，噪声系数含量较大，需要对靠近SUREShrink的系数或者距离VisuShrink阈值较远的系数进行较大比例的萎缩；而对靠近VisuShrink阈值的系数进行萎缩的程度相对较小。图4可以看出抛物型模糊隶属度函数曲线在靠近a也即SUREShrink阈值的时候斜率较小，函数值较小，可以实现对靠近该阈值的系数进行较大比例的萎缩，而在靠近b也即VisuShrink阈值的时候斜率又较大，实现了对靠近该阈值的系数进行小比例的萎缩，函数曲线最符合去噪处理要求，因此选用抛物型模糊分布。

图4　三种不同的偏大型模糊分布

当采用抛物型的隶属函数时，相应的f（imfk，t）可以表示为：

综上所述，基于EEMD和模糊阈值去噪方法的具体步骤可以分为：

Step1对含噪信号经过EEMD分解，表示为（2）；

Step 2通过（6）式得到含噪信号和每一个IMF的余弦相似度S（k），并将Kth定为S（k）的首个极小值的后一个位置；

Step 3对噪声主导模态分量分别利用式（7）和式（8），求得模糊区域的上下边界，然后利用式（10）求得处理后的噪声主导模态分量imfk′（t）；

Step 4将所有的IMF合并得到消噪信号，即：

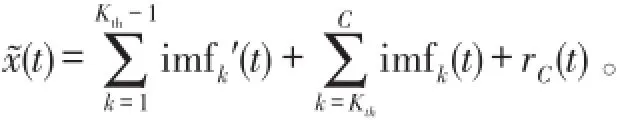
3　实验结果与分析

为了分析所提方法的去噪性能，分别对仿真信号和真实信号进行了去噪实验。利用matlab7.0中的wnoise函数生成三种典型的仿真信号，分别为“Blocks”，“Bumps”，“HeavySine”，真实信号选用MIT-BIH数据库的ECG信号。为了对比去噪效果，分别利用小波半软阈值方法［13］、文献［14］提出的基于EMD的软阈值方法（EMD-Soft）和文献［8］提出的基于EMD的间隔阈值方法（EMD-IT）与本文方法进行比较。在利用小波软阈值法去噪时，小波基选用“sym4”，分解层数为3层；EMDSoft和EMD-IT方法均采用经典的连续均方误差法确定要处理的层数，并且以式（7）得到的通用阈值作为处理阈值；本文方的参数设定为：噪声标准差为0.4，添加噪声的次数为20。另外，本文选取去噪后输出信号的信噪比SNR和均方根误差RMSE作为去噪性能的评价指标：信噪比越大，均方根误差越小，表明去噪效果越好。

3.1含噪仿真信号去噪

在该实验中，利用Matlab中的wnoise函数生成信号长度（即采样点数）N取为2 048的仿真信号“Blocks”信号、“Bumps”信号、“Heavy Sine”信号。使用awgn函数向信号中添加白噪声，分别生成信噪比为-5 dB，0 dB、5 dB、10 dB的含噪信号。再分别用小波半软阈值法，EMD-Soft法，EMD-IT法和本文方法进行去噪处理并计算其SNR和RMSE。重复实验2 000次，分别求得SNR和RMSE的平均值，结果如表2所示。

表2　仿真信号的去噪结果

图5表示在信噪比为10 dB时，四种方法对“Bumps”信号某次进行去噪的效果。从表2中也可以看出当信噪比为10 dB时，Bumps信号经过本文方法去噪之后效果最好，与小波半软阈值法相比SNR高出0.103 2 dB，RMSE降低了0.001 6；与EMD-Soft方法相比SNR高出1.196 7 dB，RMSE降低了0.019 2；与EMD-IT方法相比SNR高出0.339 4 dB，RMSE降低了0.005 2。图6～图8表示当信噪比为-5 dB～10 dB时，四种方法对Blocks信号，Bumps信号和Heavy Sine信号进行去噪时的SNR曲线。图中可以看出本文方法对三种仿真信号进行去噪时，整体上要优于其他三种方法。

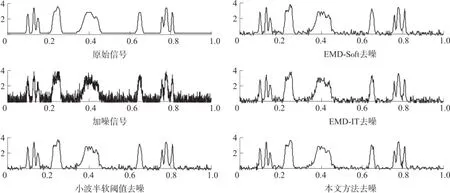
图5　四种方法对Bumps信号的去噪效果

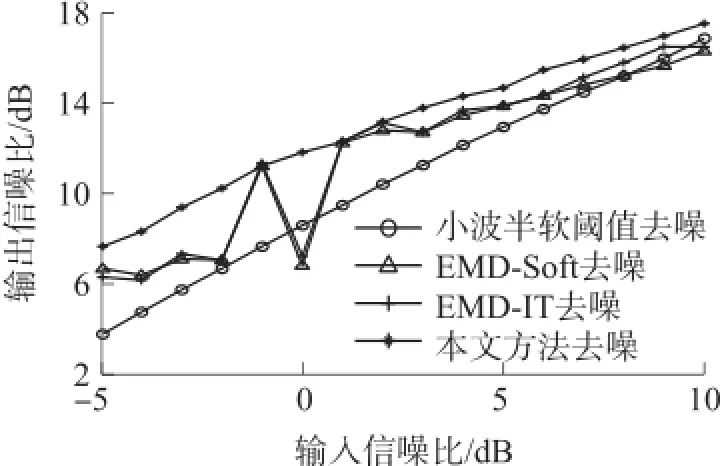
图6　不同信噪比下的Blocks信号去噪后的SNR曲线

图7　不同信噪比下的Bumps信号去噪

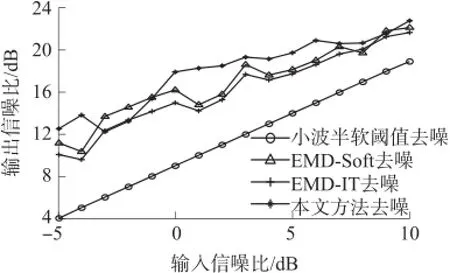
图8　不同信噪比下的Heavy Sine信号

3.2实际信号去噪

为了分析本文所提方法对实际信号的去噪性能，采用MIT-BIH数据库的ECG数据进行实验，截取信号的长度（即采样点数）为2 048。心电信号中含有的噪声大多为工频干扰，基线漂移，肌电干扰等。肌电干扰主要由人体活动肌肉紧张收缩引起，频率范围为0～1 kHz，频谱特性近似于高斯白噪声［15］，可以使用Matlab中的awgn函数向信号中添加高斯白噪声来模拟；以幅度为0.1的50 Hz和60 Hz的正弦波模拟工频干扰；以幅度为0.01的0.15 Hz的正弦信号模拟基线漂移［16］。表3中给出了在三种噪声影响下，用不同强度的高斯白噪声模拟肌电干扰得到原始含噪信号的信噪比分别为-2.27 dB，1.34 dB，5.07 dB，11.45 dB时，分别用四种方法进行去噪得到的SNR和RMSE结果。实验表明当对ECG信号进行去噪时，本文方法要明显优于另外三种方法，去噪效果有所提高。图9表示当含噪信号的信噪比为5.07 dB时，对该含噪信号分别利用四种方法进行去噪的结果。可以看出，本文所提方法去噪后，信号的细节部分和突变部分保持较好，与其他方法去噪的效果相比，信号失真较少。由表3可以知道，当信噪比为5.07 dB时，本文方法的去噪效果最好，与小波半软阈值方法相比，SNR高出1.50 dB，RMSE降低了0.006 2，与EMD-Soft方法相比SNR高出2.64 dB，RMSE降低了0.010 7，与EMD-IT方法相比SNR高出2.64 dB，RMSE降低了0.010 7。

表3　真实信号消噪效果比较

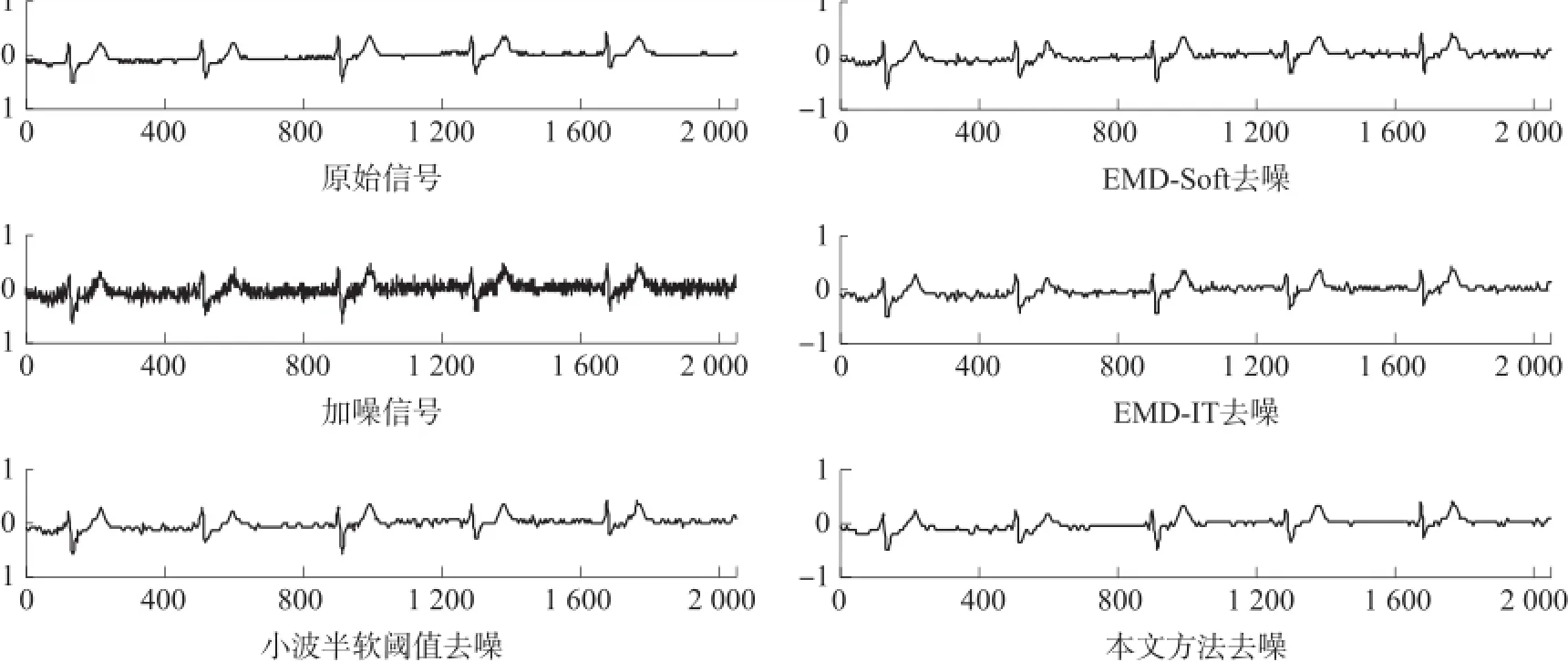
图9　ECG信号消噪效果比较

4　结束语

为了提高实际中非平稳非线性信号的去噪效果，结合EEMD具有自适应的时频分析特性，本文提出了一种基于夹角余弦和模糊阈值的EEMD去噪方法。精准地确定了EEMD分解后的IMF分量中噪声主导模态和信号主导模态的分界位置，并采用模糊阈值法对噪声主导模态进行处理。为了验证该方法的去噪性能，选择了小波半软阈值法、EMD-Soft方法和EMD-IT方法进行比较。实验结果表明，本文方法的去噪性能总体上优于其他三种方法，并且对含噪的ECG信号的去噪实验也进一步证明了本文方法去噪地有效性。

［1］曹京京，胡辽林，赵瑞.一种改进小波阈值函数的光纤光栅传感信号去噪方法［J］.传感技术学报，2015，28（4）：521-525.

［2］胡欢，余永，王慧，等.HHT算法在压电陶瓷驱动器的微纳米位移传感器中的应用［J］.传感技术学报，2014，27（4）：456-462.

［3］Huang N E，Shen Z，Long S R，et al.The Empirical Mode Decom⁃position and the Hilbert Spectrum for Nonlinear and Non-Station⁃ary Time Series Analysis［C］//Proceedings of the Royal Society of London A：Mathematical，Physical and Engineering Sciences.The Royal Society，1998，454（1971）：903-995.

［4］Boudraa A O，Cexus J C.EMD-Based Signal Filtering［J］.IEEE Transactions on Instrumentation and Measurement，2007，56（6）：2196-2202.

［5］席旭刚，武昊，罗志增.基于EMD自相关的表面肌电信号消噪方法［J］.仪器仪表学报，2014，35（11）：2494-2500.

［6］Ayenu-Prah A，Attoh-Okine N.A Criterion for Selecting Relevant Intrinsic Mode Functions in Empirical Mode Decomposition［J］. Advances in Adaptive Data Analysis，2010，2（1）：1-24.

［7］Tang Y W，Tai C C，Su C C，et al.A Correlated Empirical Mode Decomposition Method for Partial Discharge Signal Denoising［J］. Measurement Science and Technology，2010，21（8）：085106.

［8］Kopsinis Y，McLaughlin S.Development of EMD-Based Denois⁃ing Methods Inspired by Wavelet Thresholding［J］.IEEE Transac⁃tions on Signal Processing，2009，57（4）：1351-1362.

［9］马玉良，许明珍，佘青山，等.基于自适应阈值的脑电信号去噪方法［J］.传感技术学报，2014，27（10）：1368-1372.

［10］Yang G，Liu Y，Wang Y，et al.EMD Interval Thresholding Denois⁃ing Based on Similarity Measure to Select Relevant Modes［J］.Sig⁃nal Processing，2015，109：95-109.

［11］关新平，刘冬，唐英干，等.基于局部方差的模糊小波阈值图像去噪［J］.系统工程与电子技术，2006，28（5）：650-653.

［12］ÜstündaǧM，Gökbulut M，Şengür A，et al.Denoising of Weak ECG Signals by Using Wavelet Analysis and Fuzzy Thresholding［J］.Network Modeling Analysis in Health Informatics&Bioinfor⁃matics，2012，1（4）：135-140.

［13］邢国泉，叶华山，张玉霞，等.基于一种新的阈值函数的小波图像去噪方法［J］.生物医学工程学杂志，2013（4）：743-747.

［14］Boudraa A O，Cexus J C，Saidi Z.EMD-Based Signal Noise Re⁃duction［J］.International Journal of Signal Processing，2004，1（1）：33-37.

［15］宋立新，王祁，王玉静.基于Hilbert-Huang变换的ECG信号降噪方法［J］.传感技术学报，2006，19（6）：2578-2581.

［16］Friesen G M，Jannett T C，Jadallah M A，et al.A Comparison of the Noise Sensitivity of Nine QRS Detection Algorithms［J］.IEEE Transactions on Biomedical Engineering，1990，37（1）：85-98.

马子骥（1978-）男，汉族，湖南长沙人，博士，讲师，IEEE会员，IEICE编委。主要研究领域是无线通信技术，数字信号处理，广播系统及传感器技术，zijima@hnu. edu.cn；

郭帅锋（1992-）男，汉族，河南汝州人，硕士研究生，主要从事数字信号去噪处理以及复杂系统建模的研究，hnugsf@ sina.com；

李艳福（1988-），男，汉族，河南偃师人，博士研究生。主要从事轨道交通数字信号处理，数据挖掘，经验模态分解相关研究，837139089@qq.com。

EEACC：722010.3969/j.issn.1004-1699.2016.06.014

基于夹角余弦和模糊阈值的EEMD去噪方法*

马子骥*，郭帅锋，李艳福
（湖南大学电气与信息工程学院，长沙410082）

针对非线性非平稳信号的去噪问题，结合EEMD分解信号的自适应特性，提出一种基于夹角余弦和模糊阈值的去噪方法。首先用夹角余弦法计算各个本征模态函数（IMF）与观测信号之间的相似度，以相似度曲线的首个极小值的后一个位置为分界点将分解出的IMF分为噪声主导模态和信号主导模态；然后根据VisuShrink阈值易“过扼杀”细节系数和SUREShrink阈值易“过保留”噪声系数的特点，利用模糊阈值对噪声主导的IMF进行处理；最后将所有的IMF重构得到消噪信号。分别采用仿真信号和真实ECG信号进行去噪实验。结果表明，所提方法在整体性能上优于小波半软阈值方法、基于EMD的软阈值（EMD-Soft）和间隔阈值（EMD-IT）方法，是一种有效的去噪方法。

信号去噪；聚合经验模态分解；本征模态函数；夹角余弦；模糊阈值

TN911.72

A

1004-1699（2016）06-0872-08

2015-11-30修改日期：2016-02-18

项目来源：中央国有资本经营预算项目（财企［2013］470号）；中央高校基本科研项目（2014-004）；国家自然科学基金项目（61172089）；湖南省科技计划项目（2014WK3001）；中国博士后科研基金项目（2014M562100）；湖南省科技计划重点项目（2015JC3053）；湖南省自然科学基金项目（14JJ4026）