Temperature Compensation Algorithm Based on Least Squares Curve Fitting in Flow Measurement*

SHAO Xianhe，LU Zhicheng，WANG Zhu（Harbin Institute of Technology at Weihai，School of Information and Electrical Engineering，Weihai Shandong 264209，China）



Temperature Compensation Algorithm Based on Least Squares Curve Fitting in Flow Measurement*

SHAO Xianhe*，LU Zhicheng，WANG Zhu
（Harbin Institute of Technology at Weihai，School of Information and Electrical Engineering，Weihai Shandong 264209，China）

There are serious non-linear errors in flow measurement of ultrasonic heat meter utilizing time difference method.This paper gives detailed calculation and analysis to explain that the errors are caused by the changes of flu⁃id temperature.To solve this problem，a temperature compensation algorithm based on least squares curve fitting is proposed.Temperature compensation is realized through establishing a non-linear mapping model between flow rate and fluid temperature.However，each meter has different metrological properties.So this paper puts forward an er⁃ror second-order correction algorithm further.The error of flow rate at current temperature is calculated according to the errors at two adjacent temperature spots and variable weight.The flow measurement global optimization is real⁃ized by second-order correction.Experimental verification showed that flow measurement error was between±2.0%. So this algorithm has definite value to engineering application.

ultrasonic heat meter；flow measurement；temperature compensation；least squares surface fitting；error correction

时差法超声波式热量表是通过测量超声波顺、逆两向的时间差计算流量，然后代入焓差法或K系数法公式计算出热量［1］。流量计量的精确度直接决定着热量计量的精确度［2］。超声波式热量表通常工作在30℃～80℃的环境下。而超声波在水中的传播速度随温度呈非线性变化，从而给流量计量带来非线性误差。因此，在用超声波进行流量计量时，必须要考虑温度对超声波传播速度的影响。同时，温度变化还会对管道内流体的流动形态产生影响。目前，超声波式热量表多采用查表法进行温度补偿。查表法速度快，但是数据量大，对单片机的存储容量要求高，而且只能实现局部最优。文献［3］通过建模仿真和现场实验，提出了基于BP神经网络的温度补偿算法，补偿效果较好，但是选取的样本点（温度和流量）少，而且没有考虑超声波式热量表自身计量特性的差异，不能进行二次修正，因此不适合在实际生产中推广应用。

针对上述问题，通过分析温度对时差法流量计量精确度的影响，提出了基于最小二乘曲面拟合的温度补偿算法和多温度点误差二次修正算法，不仅实现了对流量计量的温度补偿，而且可以对温度补偿后的每块超声波式热量表进行误差二次修正，提高了流量计量的精确度和稳定性，可在工业生产中推广应用。

1　时差法超声波式热量表流量计量误差分析

1.1时差法流量测量原理

U型声道时差法流量测量管道结构如图1所示［4］。

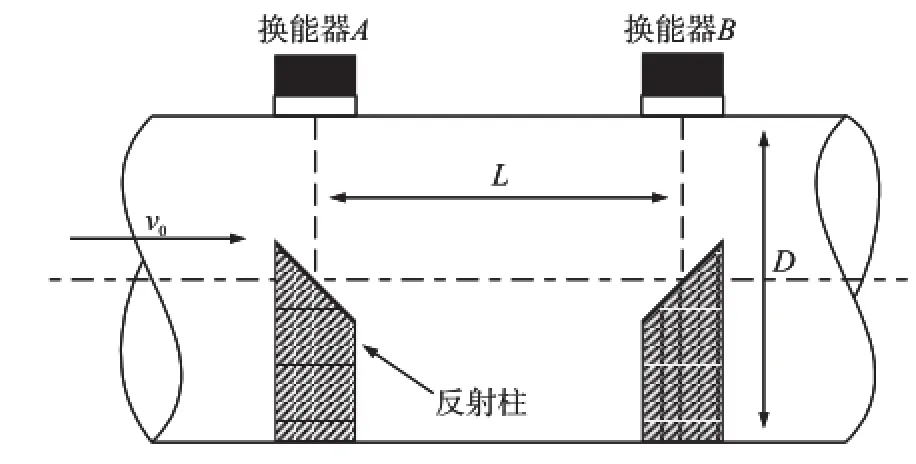
图1　U型声道时差法流量测量原理示意图

换能器A和B分别安装在管道上游和下游，间距为L。A和B交替收发超声波信号实现时间差的测量。假设管道内径为D，流体流速为v0，流体静止时超声波在流体中传播的波速为c。当超声波顺流传播时，超声波从发射端发出经反射柱两次反射到达接收端的时间为t1。逆流传播时，从发射端到达接收端的时间为t2。反射柱为不锈钢材料，会改变原有的流速分布。但是，安装反射柱后的流速分布场是确定的，可以根据其分布进行流速补偿。而且通过反射柱可以增加超声波传播距离、增大传播时间差减小流速测量误差。

由时差法原理可知流体体积流量V为：

式中，K为流速修正系数，可根据流体的流动形态确定。

1.2温度对超声波传播速度的影响

由式（1）可知，流体的体积流量与超声波传播速度的平方呈线性关系。而超声波传播速度随温度呈非线性变化［5］，其变化趋势如图2所示。

若仅考虑超声波传播速度对流体体积计量结果的影响，则式（1）可简化为：

假设在程序中使用超声波在74℃的流体中的传播速度（1 555.47 m/s）计算流体体积，而当流体真实温度为30℃时，超声波在流体中传播的波速为1 509.44 m/s。则流体体积流量计量误差为：

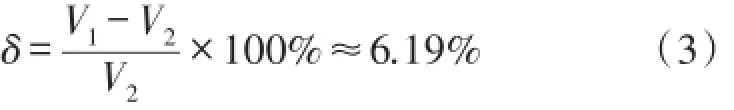
式中，V1为使用超声波在74℃的流体中的传播速度计算得到的流体体积流量，V2为使用超声波在30℃的流体中的传播速度计算得到的流体体积流量。

对于高精确度的流量测量，这个误差是不可忽略的。

图2　超声波传播速度随温度变化图

1.3温度对管道内流体流动形态的影响

管道内流体因粘滞性而具有两种流动形态：层流和紊流。液体质点作有条不紊的运动，彼此不相掺杂的形态称为层流。液体质点作不规则运动、互相混掺、轨迹曲折混乱的形态称为紊流［6］。

图3为层流与紊流流速分布图。两种流动形态下管道轴心线流速与面流速之间的关系分别为：

层流：K=v/v0=0.5

紊流：K=v/v0=0.75～0.9（为简化计算，一般取0.825。由此带来的误差可通过温度补偿消除）

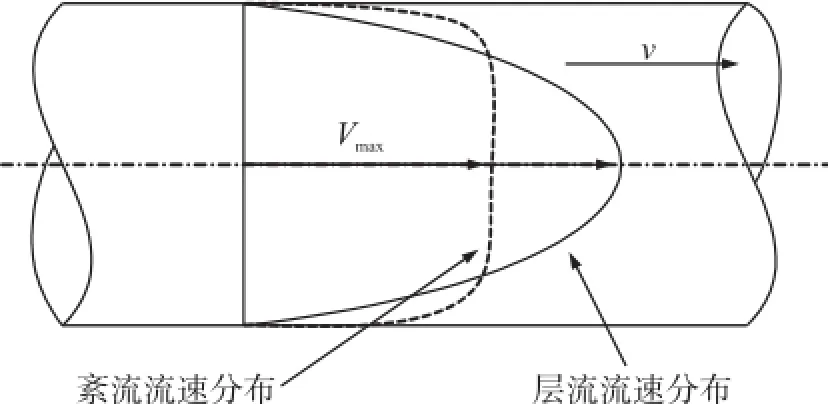
图3　层流与紊流流速分布

流体的流动形态可由雷诺数Re判别。在工程计算中，当Re≤2 000时是层流；当Re＞2 000时是紊流。对于圆形截面管道，雷诺数Re可由下式计算：

式中，v¯为管道内流体的平均流速；d为管道内径；υ为流体的运动粘度。由于流体的运动粘度与温度存在非线性关系。因此，当管道内流体流速和管径恒定时，雷诺数Re的值随温度呈非线性变化［7］。

假设D=20 mm，v¯为0.05 m/s，流体温度为30℃，运动粘度υ为8.009×10-7m2/s［8］。按式（4）计算得Re为1 248.60，流体的流动形态为层流。流速修正系数K取0.5。当温度升高到80℃时，运动粘度υ为3.650×10-7m2/s，计算得Re为2 739.73，流体的流动形态为紊流。流速修正系数K取0.825。则流体体积流量计量误差为：

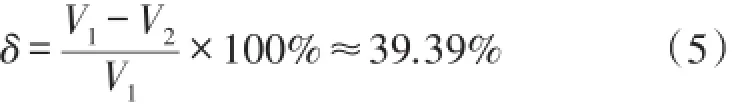
式中，V1为流体温度为80℃时的流体体积流量，V2为流体温度为30℃时的流体体积流量。

管道内流体的分布规律极为复杂。为了计算方便，通常认为超声波式热量表在全量程内始终工作在一种状态，在计算流量时流速修正系数K取固定值。但是，当温度变化时，管道内流体的流动形态可能会改变，给流体体积计量带来较大误差。

由上述分析可知，温度对超声波流量计量的精确度有着不可忽视的影响。在高精确度的流量计量中，必须要进行温度补偿。

2　最小二乘曲面拟合原理

2.1曲面模型的选择

对同一组采样数据，不同的曲面模型拟合效果存在较大差异。我们可以通过以下参数来评价各曲面的拟合效果，从而选择最佳拟合曲面模型。

SSE（误差平方和）：曲面预测值和采样值的误差平方和。

RMSE（均方根误差）：曲面预测值和采样值的误差均方根。

R-square（确定系数）：曲面预测值和采样数据均值之差的平方和与采样值和采样数据均值之差的平方和的比值。

当SSE和RMSE越小，R-square越接近1时，曲面模型的拟合效果越好［9］。

2.2曲面方程的求解

通过比较多项式逼近和指数逼近的拟合效果，最终选择二元二次多项式作为拟合曲面模型，其规范化表达式为：

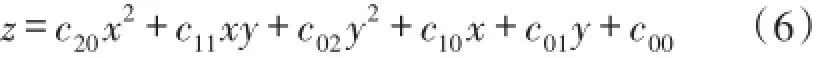
式中，x，y，z是采集的数据，c20，c11，c02，c10，c01，c00是待定系数。

该曲面模型的误差平方和为：

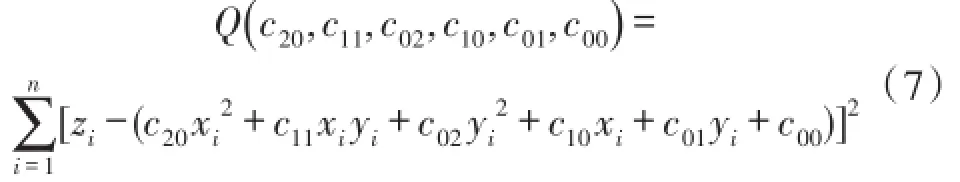
式中，（xi，yi，zi），i=1，2，…，n是采样数据。

求解二元二次多项式待定系数的原则是使曲面模型的误差平方和达到最小［10］。由微积分知识可知，该问题即求解六元函数Q（c20，c11，c02，c10，c01，c00）的极值，联立方程：

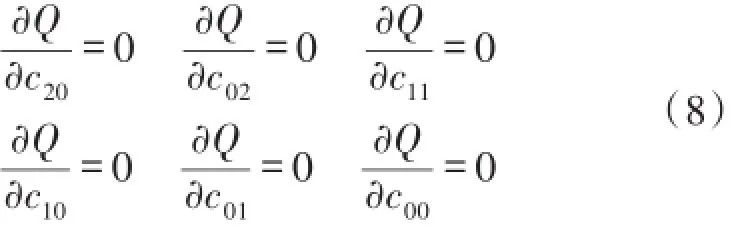
可解得待定系数［11］。

3　流量检定实验及数据分析

3.1实验与测试平台

实验平台为三宇热能表检定装置，可用于检定超声波热量表流量计量的精确度。检测台的流量计量精确度为0.000 1 m3/h，温度测量精确度为0.1℃。实验中选用5块DN20的超声波式热量表，量程为0～5.0 m3/h。

3.2实验方案

3.2.1数据采集

本实验通过建立温度和流量之间的非线性映射模型实现流量计量的温度补偿，因此需要采集检测台和未经温度补偿的超声波式热量表在不同温度、流量下测得的瞬时流量值，为曲面模型建模提供样本数据，同时也验证温度对超声波式热量表流量计量精确度的影响。实验中采样的温度点有（单位：℃）：30、35、40、45、50、55、60、65、70、75，流量点（单位：m3/h）有：0.05、0.1、0.25、0.3、0.4、0.5、0.6、0.75、0.8、0.9、1.0、1.1、1.2、1.3、1.4、1.6、1.8、2.0、2.2、2.4、2.6、2.8、3.0、3.5、4.0、4.5。

在采集数据时，要等到瞬时流量稳定之后再开始记录。对每块超声波热量表在不同温度、流量下测得的瞬时流量值至少采集4次，然后取平均值作为该温度、流量下的测量值。检测台测得的瞬时流量值作为目标值。

从图4可以看出，流量计量的精确度受温度的影响。在同一流量点下，流量计量误差随着温度的升高而减小。流量计量的精确度还与瞬时流量有关。相同温度下，瞬时流量越小，误差越大。当瞬时流量小于0.5 m3/h时，误差随着瞬时流量的增大迅速减小。当瞬时流量大于0.5 m3/h时，误差变化平缓，趋于稳定。因此采取按瞬时流量分段曲面拟合的方法改善拟合效果。

图4　流量计量误差随温度、流量变化曲线图

3.2.2分段建模

根据最小二乘曲面拟合原理，分别求解各拟合曲面模型。通过比较各拟合曲面模型的评价参数，选择拟合效果最好的二元二次多项式曲面模型。其表达式为：

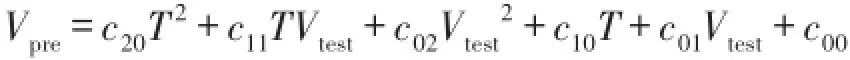
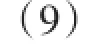
式中，Vpre为预测瞬时流量值，Vtest为超声波式热量表实测的瞬时流量均值，T为流体温度。

以0.1 m3/h、0.6 m3/h、1.2 m3/h为界分段拟合。解得不同瞬时流量区间的拟合曲面模型的待定系数和评价参数如表1和表2所示。

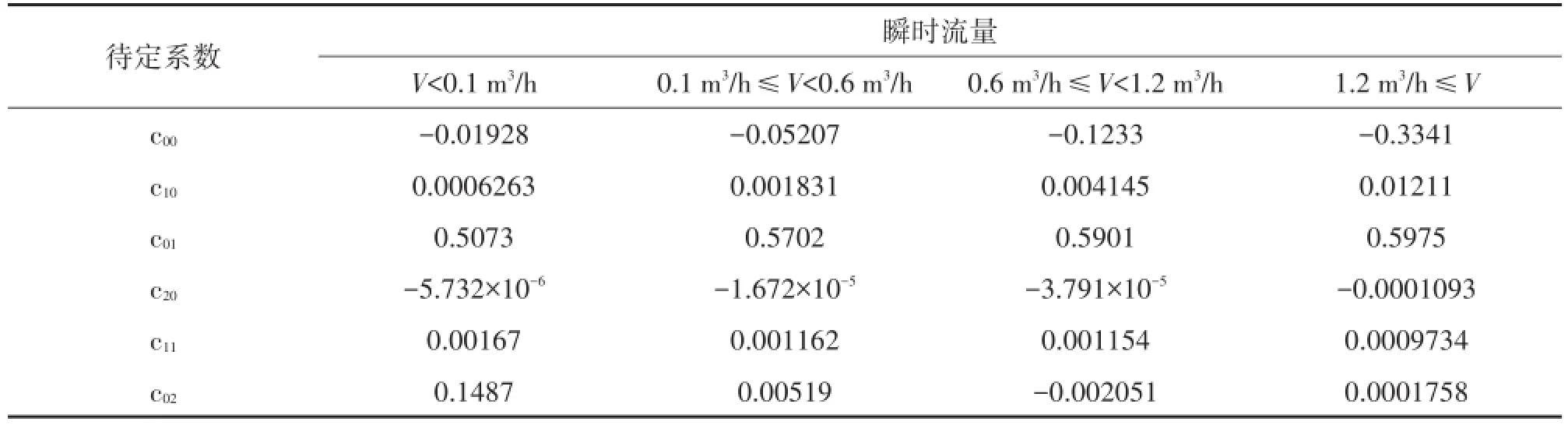
表1　拟合曲面模型待定系数

表2　拟合曲面模型评价指标

（3）仿真验证

建模完成之后，把之前采集的样本数据代入对应的拟合曲面模型。在不同温度、流量下预测值与目标值的误差如图5所示。

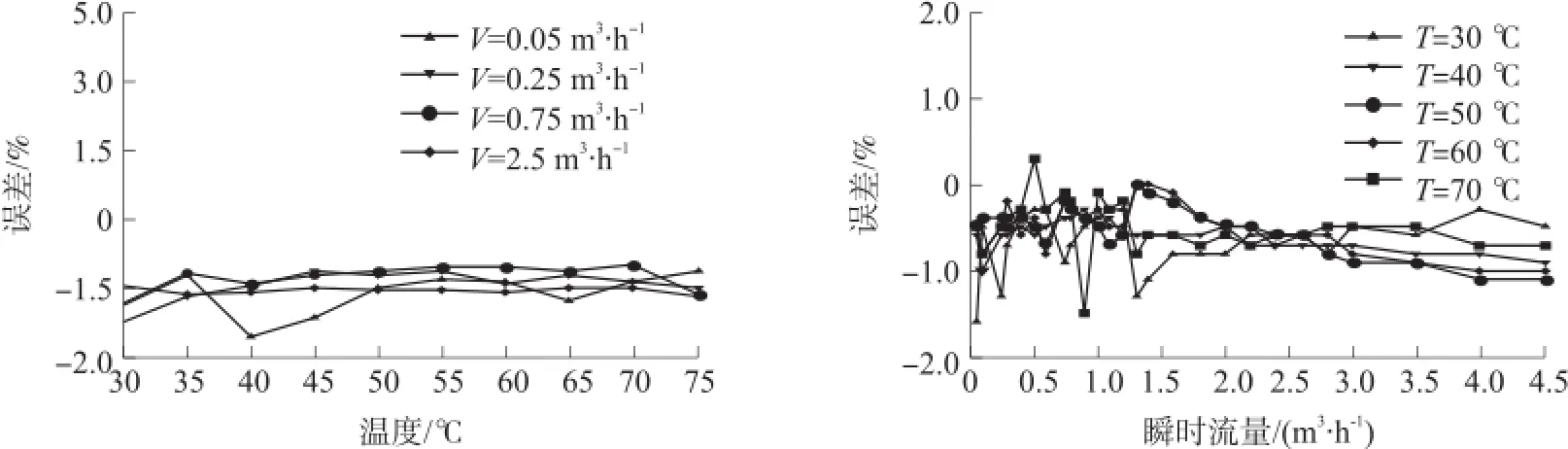
图5　不同温度、流量下预测值和目标值的误差曲线

从图5可以看出，基于最小二乘曲面拟合的温度补偿算法补偿效果显著。不同温度、流量下预测值和目标值的误差在-2%到1%之间波动，达到超声波式热量表二级表的流量计量误差要求。当瞬时流量小于1.2 m3/h时，误差波动较大。当瞬时流量大于1.2 m3/h时，误差趋于稳定。

图6　最小二乘曲面拟合算法温度补偿后流量计量误曲线

4　实验验证及数据分析

4.1算法移植

为了实现实时温度补偿，将拟合曲面模型移植到超声波式热量表程序中。当超声波式热量表测得未经温度补偿的瞬时流量和流体温度时，先根据实测瞬时流量所在区间选择对应的曲面模型，然后把实测瞬时流量和流体温度代入曲面方程计算得到预测流量，实现流量计量实时温度补偿［12］。

4.2实验验证及数据分析

利用检测台对分别使用最小二乘曲面拟合算法和经过二次修正后的查表法进行温度补偿的超声波式热量表进行流量检定实验。根据JJG225检定规程和行业标准，流量检定点（单位：m3/h）选择：0.05、0.25、0.75、2.5。使用两种不同温度补偿方法的超声波式热量表在不同温度的流量计量误差如图5、图6所示。

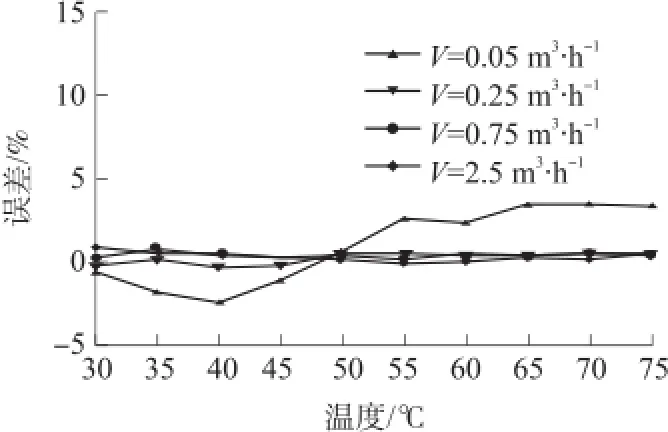
图7　查表法温度补偿后流量计量误差曲线

表4　查表法与最小二乘曲面拟合算法流量计量误差比较

由图6、图7及表4可知：在小流量点时，使用查表法温度补偿的超声波式热量表流量计量误差在±3%以内，误差绝对值均值为2.15%，误差方差为4.80，流量测量值波动大，补偿效果不稳定。使用最小二乘曲面拟合算法温度补偿的超声波式热量表流量计量误差在±2.0%以内，误差绝对值均值为0.72%，误差方差为0.16。相比查表法，最小二乘曲面拟合算法整体误差更小，补偿效果更稳定。在大流量点时，两种方法效果相当。从表3可以看出使用最小二乘曲面拟合算法温度补偿后的超声波式热量表在大流量点可达到1级表水平，在小流量点可达到2级表水平。

4.3多温度点误差二次修正算法

由于硬件原因，不同超声波式热量表在计量特性方面存在差异。在数据采集和实验验证过程中，我们发现个别热量表在小流量点的流量计量误差与其他热量表相比整体偏大。在使用最小二乘曲面拟合算法温度补偿后，该表在小流量点的流量计量误差仍然偏大，甚至超出±3%。因此，有必要对其进行二次修正。

当温度变化较大时，热量表在小流量点的流量计量误差变化较大，比如在低温下流量计量误差为正，在高温下可能为负。如果只根据单个温度点的流量计量误差对整体进行误差修正，可能会导致其他温度点的流量计量误差变大，即只能实现局部最优。因此考虑采取多温度点误差二次修正的方法实现流量计量的全局优化。

当温度变化较小时，热量表的流量计量误差变化几乎可以忽略不计。所以在一定温度范围内可以按照相同流量计量误差进行二次修正。本实验中，选取4个温度点，在相邻两个温度点之间每3℃按照同一个流量计量误差进行修正。假设通过检测台分别测得热量表在33℃和48℃的流量计量误差α和β。在35℃和49℃之间以3℃为步长划分为5小段。本实验中各温度区间的误差权值取值如下：（1，0），（0.8，0.2），（0.6，0.4），（0.4，0.6），（0.2，0.8），（0，1）。小于35℃按误差α修正；在35℃～38℃之间，按0.8α+0.2β修正；在35℃～38℃之间，按0.6α+ 0.4β修正；依此类推，在46℃～49℃之间，按误差β修正。误差权值根据当前温度越接近哪个温度点，对应的误差权值越大的原则来确定。此外，还选择63℃和77℃作为修正点，确保实现全局修正。在其他相邻温度点之间也是根据相邻两个温度点的流量计量误差和误差权值合成修正值。

多温度点误差二次修正前后对比如图8所示。

图8　0.05 m3/h下多温度点误差二次修正前后流量计量误差对比

查表法是对时差法流量计算公式中的各项参数补偿，包括对超声波波速的补偿，对流速修正系数的补偿等。而最小二乘曲面拟合算法和BP神经网络算法都是通过建模直接对不同温度（30℃～80℃）、瞬时流量（0～5.0 m3/h）下的流量计量结果补偿。显然，后者采样数据更大。查表法速度更快，但是精度偏低。BP神经网络算法建模复杂，而且由于模型的特殊性，很难对误差进行二次修正。最小二乘曲面拟合算法简单易行，而且可以对误差进行二次修正，符合生产实际和需求。

5　结论

通过理论分析和实验验证得出，温度对超声波式热量表中流量计量的精确度有着不可忽视的影响。在高精确度的测量中，必须要进行温度补偿。提出了基于最小二乘曲面拟合的温度补偿算法，并通过实验证明最小二乘曲面拟合算法可以实现超声波式热量表中流量计量的温度补偿。在小流量点补偿效果比二次修正后的查表法更稳定、更好。在实现温度补偿的基础上，针对超声波式热量表自身计量特性的差异提出了多温度点误差二次修正算法，提高了算法的通用性，适合在工业生产中推广应用。

［1］Yin-Jing G，Zhi-Wen L，Yuan Z.Design of Transit-Time Differ⁃ence Ultrasonic Heat Meter Based on TDC-GP21［J］.Journal of Measurement Science and Instrnmentation，2012：14-17.

［2］Choi H M，Yoon B R，Kim C G，et al.Evaluation of Flowmeters for Heat Metering［J］.Flow Measurement and Instrumentation，2011，22（5）：475-481.

［3］崔晓志，王翥.超声波热量表流量计量中温度补偿算法研究［J］.传感技术学报，2015，28（8）：1169-1175.

［4］黄侨蔚.带流动调整器U型声道超声波流量计流场特性仿真及优化［D］.华南理工大学，2013.

［5］赵文明，邵仙鹤，王玲，等.超声波流量测量影响因素的研究［J］.自动化仪表，2012，33（9）：80-82.

［6］王翥，崔晓志，侯春雷.超声波传感器接收信号强度非对称性分析及对策［J］.传感技术学报，2015，28（1）：81-85.

［7］李坡，李毅堂，王锡钢，等.温度补偿对超声波热量表流量测量影响的研究［J］.商品与质量：消费研究，2015.

［8］汪大鹏，吴宪平，夏卿坤.雷诺数的温度特性［J］.传动技术，2006，20（3）：11-14.

［9］.Solving Problems in Scientific Computing Using Maple and Mat⁃lab®［M］.Springer Science&Business Media，2011.

［10］Total Least Squares and Errors-in-Variables Modeling：Analysis，Algorithms and Applications［M］.Springer Science&Business Media，2013.

［11］Kumar J，Shunmugam M S.Fitting of Robust Reference Surface Based on least Absolute Deviations［J］.Precision Engineering，2007，31（2）：102-113.

［12］张艳锋，严家明.基于最小二乘法的压力传感器温度补偿算法［J］.计算机测量与控制，2008，15（12）：1870-1871.

邵仙鹤（1971-）女，通信作者，哈工大（威海）副教授，主要研究方向传感器及检测技术、模式识别等，shaoxianhe@ali⁃yun.com；

鲁志成（1991-），男，山东临沂人，哈工大（威海）信电学院研究生。研究方向为传感器及检测技术，18766312596@ 139.com。

EEACC：7320W；782010.3969/j.issn.1004-1699.2016.06.018

基于最小二乘曲面拟合的流量计量温度补偿算法*

邵仙鹤*，鲁志成，王翥
（哈尔滨工业大学（威海）信息与电气工程学院，山东威海264209）

针对时差法超声波式热量表流量计量结果受流体温度影响而存在的非线性误差问题，提出了基于最小二乘曲面拟合的温度补偿算法，通过建立温度和流量之间的非线性映射模型实现温度补偿。在实现温度补偿后，针对超声波式热量表自身计量特性的差异，进一步提出多温度点误差二次修正算法，根据相邻温度点的流量计量误差和可变权值计算当前的流量计量误差，对误差进行二次修正，实现流量计量的全局优化。实验表明，流量计量误差在±2.0%以内，具有较高的工程应用价值。

超声波式热量表；流量计量；温度补偿；最小二乘曲面拟合；误差修正

TB937；TB941

A

1004-1699（2016）06-0897-06

2015-10-07修改日期：2016-02-11

项目来源：山东省科技发展计划项目（2012GGX10110）；山东省科技发展计划项目（2013GGX10129）；山东省自然科学基金项目（ZR2014FM026）