The IMU Calibration Mathematical Modeling and Error Analysis*

ZHAO Guiling，JIANG Yuhan，LI Song（School of Geomatics，Liaoning Technical University，Fuxin Liaoning 123000，China）



The IMU Calibration Mathematical Modeling and Error Analysis*

ZHAO Guiling*，JIANG Yuhan，LI Song
（School of Geomatics，Liaoning Technical University，Fuxin Liaoning 123000，China）

The calibration path design and data processing method for inertial measurement unit（IMU）depend on IMU calibration mathematical model.Installation error is an important factor in determining the IMU calibration model.According to the different installation forms of accelerometers and gyroscopes relative to the carrier，an IMU calibration mathematical modeling method was proposed by coordinate transformation.The affects of IMU calibra⁃tion model error on angular rate and acceleration were derived.It analyzed the influence of IMU calibration model error on inertial navigation system navigation（SINS），and also designed calibration path and data processing meth⁃ods based on the position information provided by turntable.The simulation and turntable experiment results show that IMU calibration model error causes attitude error，velocity error and position error.Also，the expression form of installation error decides the navigation errors caused by IMU calibration model.

inertial measurement unit；calibration；mathematical modeling；installation error；inertial navigation system navigation

惯性测量单元IMU（Inertial Measurement Unit）是捷联惯性导航系统的核心硬件基础，其标定精度直接影响捷联惯性导航系统的工作精度［1-4］。IMU标定精度取决于IMU标定数学模型精度及基于标定模型的标定路径设计和标定数据处理方法［5-8］。而IMU实际输出轴组成的陀螺坐标系和加速度计坐标系与导航解算所在的角速度坐标系和比力坐标系之间的安装误差，决定了IMU标定数学模型的表达形式。国内外对IMU标定技术的研究，主要针对转台的性能指标或载体的机动性开展标定路径设计和参数估计算法的研究［9-11］，鲜有对标定模型本身精确性和适用性的分析与探讨，部分讨论也只是基于固定模型下分析具体参数的影响［12-13］，缺乏对模型严格准确的推导，而标定模型对于标定方法的选择、IMU性能评估以及系统的误差分配具有重要意义［14］。

不同的导航系统对IMU标定模型精度要求有多高？不同精度要求的IMU标定应该采用多高精度的数学模型？简化的IMU标定模型对系统的导航精度有多大的影响？IMU标定亟待解决这些问题。本文针对IMU标定模型的精确性、适用性等实际问题开展研究工作，以三轴一体IMU安装误差角为切入点，基于空间笛卡尔坐标系转换矩阵，建立IMU标定线性数学模型，给出模型中各个参数的物理意义，并对模型进行两种常用形式的简化。基于三轴惯性测试转台设计的IMU标定仿真和实验结果，给出了IMU简化模型误差对捷联惯性导航系统精度的影响，为不同精度的捷联惯性导航系统选择IMU标定模型奠定基础。

1　IMU标定建模

IMU主要由敏感载体角速率的陀螺和敏感载体比力的加速度计组成，其中光纤陀螺和加速度计输出脉冲与角速率和比力之间的转换模型为：

式中：

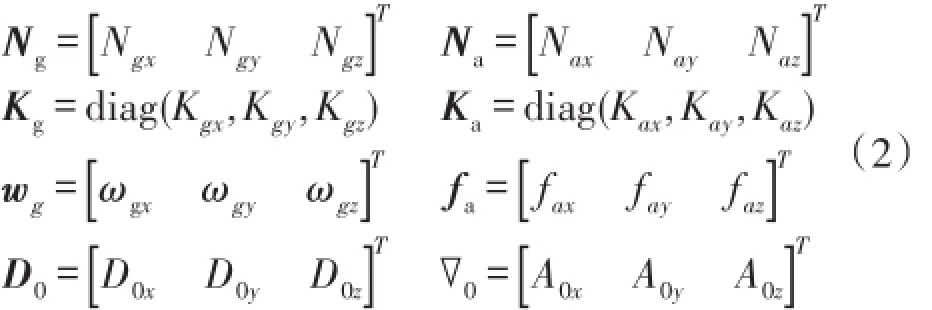
Ng和Na为光纤陀螺和加速度计的脉冲输出；wg和fa为陀螺角速率和加速度计比力；Kg和Ka为光纤陀螺和加速度计标度因数；D0和∇0为光纤陀螺和加速度计零偏。

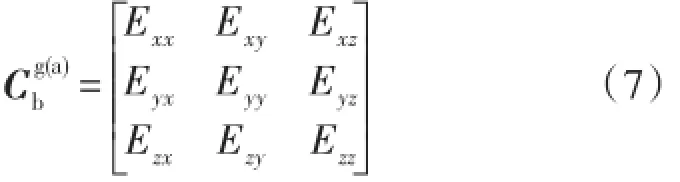
将陀螺元件和加速度计元件安装到IMU基座上时，由于元件的机械安装误差、IMU基座加工的垂直度误差、以及元件真实输入基准轴与理想输入轴之间存在的失准角误差，使得IMU实际输入轴组成的陀螺坐标系（og-xgygzg，g系）和加速度计坐标系（oa-xayaza，a系）与系统解算所在的载体坐标系（ob-xbybzb，b系）不重合。在进行系统解算时，必须将陀螺和加速度计的输出转换到载体坐标系上，因此，IMU标定数学建模问题转化为g系和a系与b系之间的空间笛卡尔坐标系转化问题。假设og和oa与ob重合为一点o，Cg（a）b为b系与g（a）系之间的转换矩阵。i，j，k表示g（a）系轴向的单位矢量，ib，jb，kb表示b系轴向的单位矢量，坐标系之间的关系如图1所示。

根据空间笛卡尔坐标系基变换公式，可得b系到g（a）系的基变换公式：

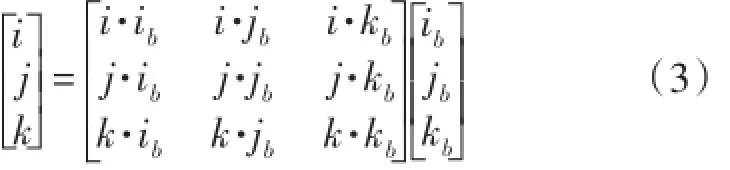
b系到g（a）系的坐标变换矩阵：

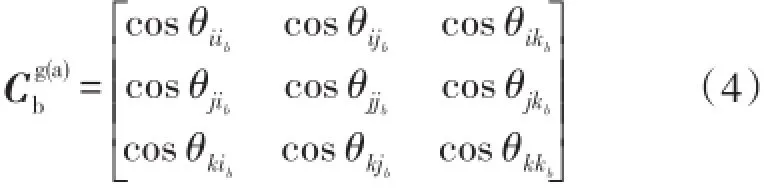
θmnb（m=i，j，k；n=i，j，k）为m与nb之间的夹角。一般为非正交矩阵，它的特点是每个行向量都是单位向量，标定路径设计与参数的求解可以利用此约束条件进行。

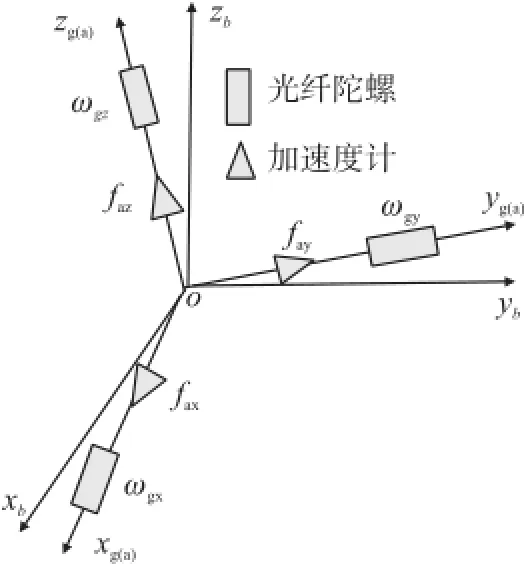
图1　IMU安装示意图

wg和fa是角速率矢量和比力矢量在g系和a系下的投影，惯性导航解算需要的是载体坐标系b系下的投影wb和fb，由于安装误差的存在，wg和fa与wb和fb之间存在如下关系：

将式（5）代入式（1），可得IMU输入输出标定数学模型为：

2　IMU标定模型简化及误差

式（4）是在IMU敏感元件任意安装下求得的坐标变换矩阵，IMU标定常采用以下两种简化形式：①假设g（a）系三个轴与b系对应轴在空间笛卡坐标系内成小角度安装变形为：

②假设g（a）系三个轴正交安装，此时，b系到g系的坐标系变换，可以通过绕不同坐标轴的三次连续转动来实现。首先绕zb轴转动ψ角形成坐标系ob-x1y1z1，再绕y1轴转动θ角形成坐标系ob-x2y2z2，最后绕x2轴转动ϕ角形成坐标系og-xgygzg。将三次转动表述成三个独立的方向余弦阵，b系到g系的变换用三个独立的方向余弦阵乘积表示。

当三次旋转角为小角度旋转时，对（9）式进行化简，并忽略二阶以上小量变形为：

式（8）和式（10）是在IMU敏感元件小角度安装误差角和正交安装下的简化，将其代入IMU标定数学模型并进行角速度和加速度的计算：

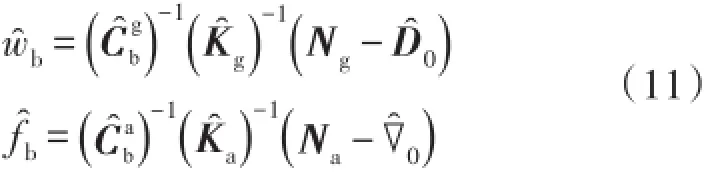
其中，x̂（x=wb，，Kg，D0，fb，Ka，∇0）表示x的计算值。将式（6）代入式（11），可得ŵb，f̂b与wb，fb之间的关系：

式（12）中，δD0=D0-D̂0，δ∇0=∇0-∇̂0。将ŵb和f̂

b代入捷联惯性导航系统误差方程：

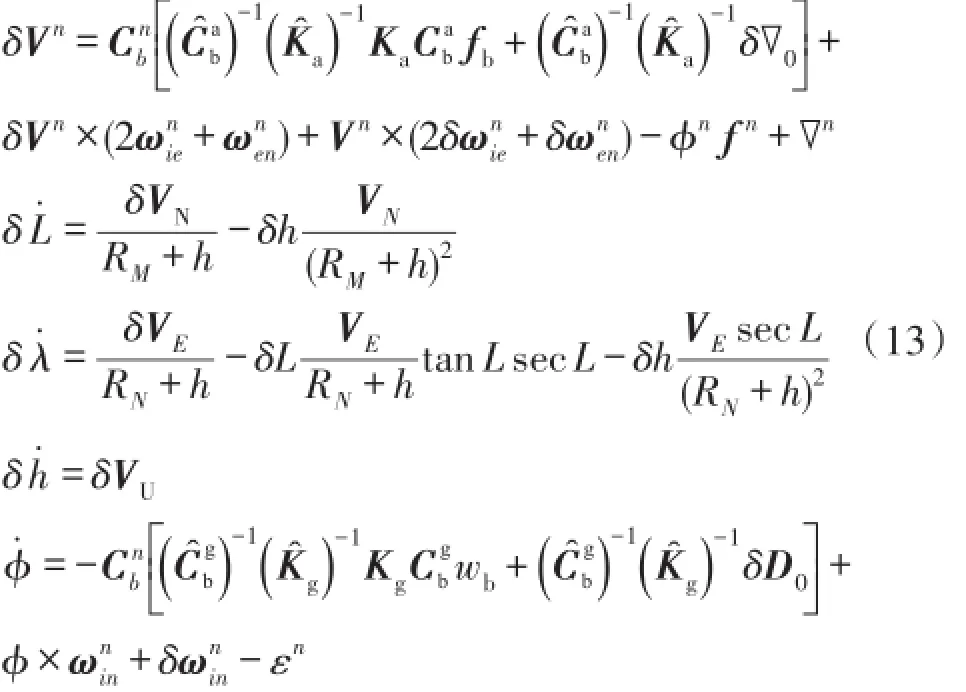
其中：Cbn为捷联转换矩阵；δVE，δVN为东向速度误差和北向速度误差；δλ、δL、δh、ϕ为经度误差、纬度误差、高度误差和姿态误差；为地球自转角速度、导航系相对地球旋转角速度、导航系相对惯性系的旋转角速度分别在导航系的投影；RN、RM为地球极半径和赤道半径；εn、∇n为等效陀螺漂移和加速度计误差。由捷联惯性导航系统误差方程式（13）可以看出，简化的IMU标定数学模型直接引起系统的速度误差、位置误差和姿态误差。

3　仿真与实验

为了分析IMU标定模型误差对捷联惯性导航系统的影响，利用三轴惯性测试转台提供的位置和速率，基于式（8）和式（10）两种简化形式，设计IMU标定路径，对IMU进行标定仿真和实验，并将标定的仿真和实验结果代入捷联惯性导航系统进行导航验证。

3.1IMU标定路径设计

三轴惯性测试转台可以提供精确的位置和速率信息，IMU标定路径设计就是利用转台提供的精确位置，激励出IMU待标定参数Kg、D0和Ka、、∇。分别设计陀螺和加速度计标定路径。矩阵0相乘使得待标定参数耦合在一起，IMU标定路径设计的关键是如何分离各个待标定参数。欲求（或）中的标定参数C，设计思想是使得第i个位置的n（n = x， y， z） 轴输出Ngn（i）（或N>an（i））与第j 个位置的n（n = x， y， z） 轴输出Ngn（j）（或Nan（j））满足如下关系：

欲求陀螺零位D0n（n=x，y，z）和加速度计零位∇0n（n=x，y，z），设计思想是使得第i个位置的n（n = x， y， z） 轴输出Ngn（i）（或Nan（i））与第j 个位置的n（n = x， y， z） 轴输出Ngn（j）（或Nan（j））满足如下关系：

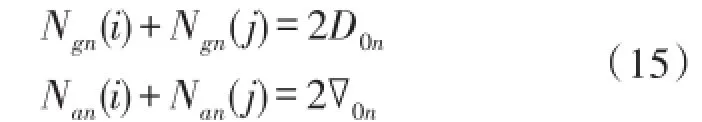
按照以上设计方案，设计的陀螺标定方案输出为：（ωie00）T、（-ωie00）T、（0ωie0）T、（0-ωie0）T、（00ωie）T、（00-ωie）T。设计的加速度计标定方案输出为：（g00）T、（-g00）T、（0g0）T、（0-g0）T、（00g）T、（00-g）T。IMU在每个位置停留5分钟，将上述位置的陀螺输入和加速度计输入分别代入式（6），根据简化形式的不同，IMU在每个位置的脉冲输出形式不同，按照式（14）和式（15）对待标定参数进行计算。

3.2计算机仿真

采用3.1设计的标定路径和计算方法对IMU标定模型误差的影响进行仿真和实验验证，将加速度计标定模型误差和陀螺标定模型误差分开讨论，并忽略转台定位误差、初始对准误差等对系统的影响，仿真条件如下：

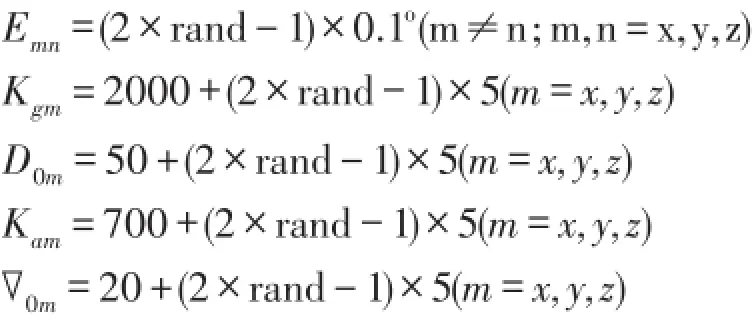
共进行50个样本的标定模型误差影响的仿真，简化的IMU标定数学模型对导航结果的影响如图2～图9所示。

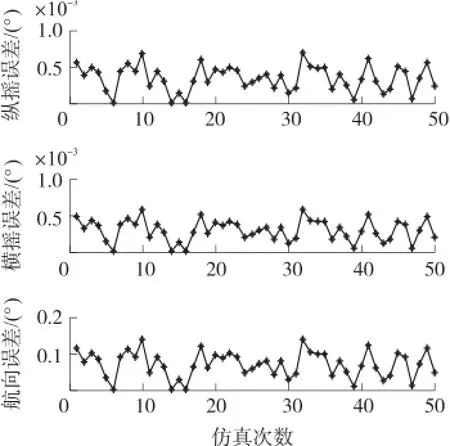
图2　陀螺简化模型一对姿态的影响

图3　陀螺简化模型一对速度和位置的影响

图4　陀螺简化模型二对姿态的影响

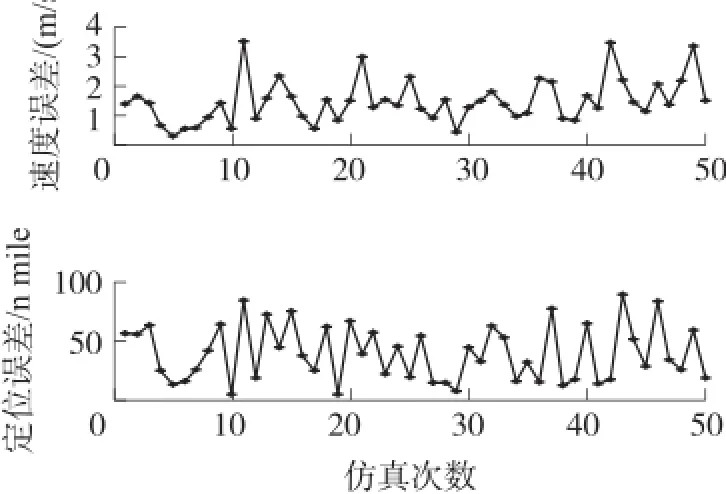
图5　陀螺简化模型二对速度和位置的影响

图6　加速度计简化模型一对姿态的影响

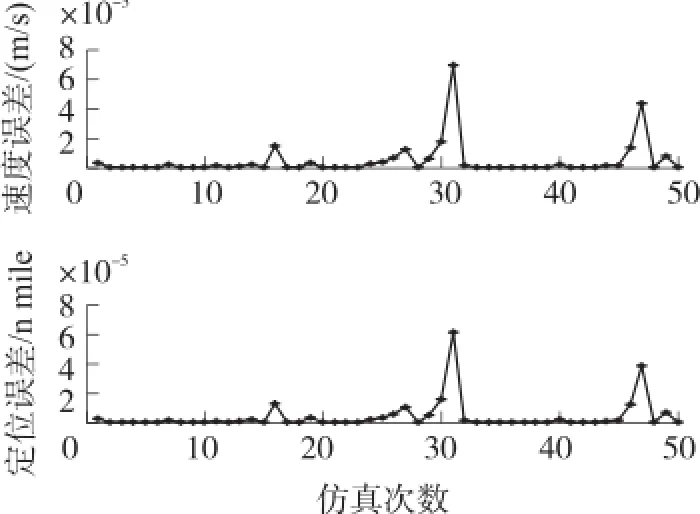
图7　加速度计简化模型一对速度和位置的影响

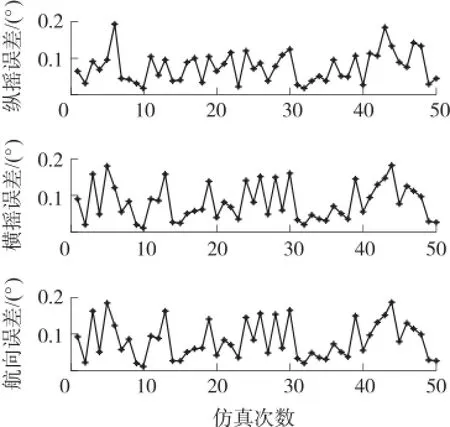
图8　加速度计简化模型二对姿态的影响

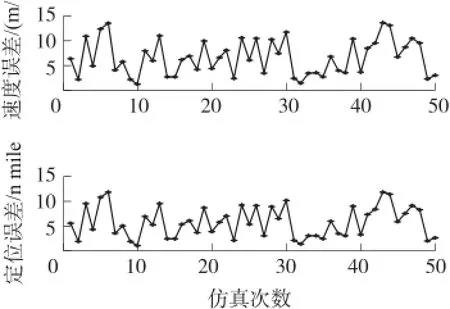
图9　加速度计简化模型二对速度和位置的影响

从仿真图2～图9和表1结果可以看出：在0.1o随机安装误差条件下，采用相同的陀螺简化标定数学模型和加速度计简化标定数学模型，陀螺标定模型引起的捷联惯性导航系统导航误差大于加速度计标定模型引起的系统导航误差。三个安装误差角形式的陀螺和加速度计标定数学模型引起的系统导航误差大于六个安装误差角形式的标定数学模型引起的系统导航误差。

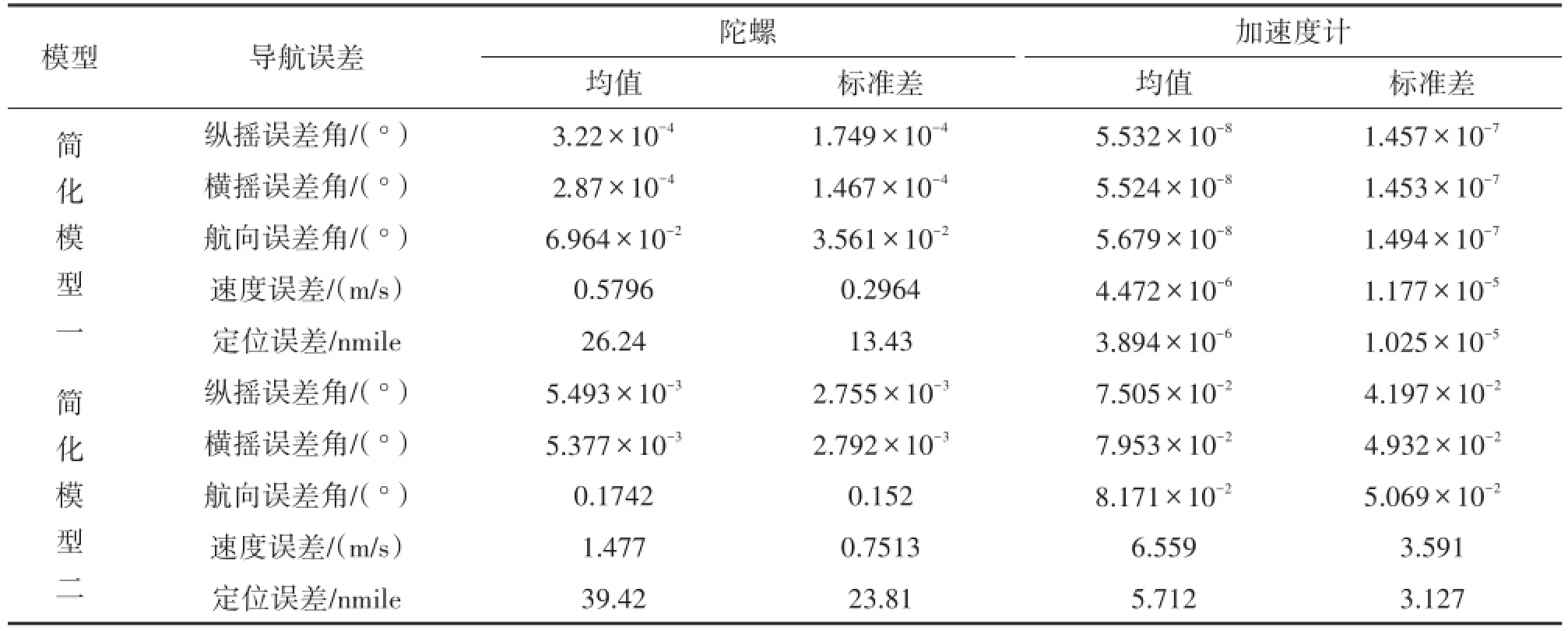
表1　 IMU简化模型对导航的影响

3.3转台实验

将光纤陀螺捷联惯性导航系统置于三轴惯性测试转台，转台角位置精度3″。控制转台按照3.1设计的IMU标定路径进行旋转，采集陀螺和加速度计输出，分别按照式（8）和式（10）两种简化的IMU标定数学模型进行标定参数计算，并将计算结果代入捷联惯性导航系统进行导航，导航结果如图10所示。

图10　导航定位误差

基于简化模型一标定出的陀螺和加速度计参数分别代入捷基于联惯性导航系统，引起的静态导航定位误差为6.10 nmile/40 h和4.16 nmile/40 h；基于简化模型二标定出的陀螺和加速度计参数分别代入捷基于联惯性导航系统，引起的静态导航定位误差为29.37 nmile/40 h和21.55 nmile/40 h。模型二引起的定位误差远大于模型一引起的定位误差，这与仿真得到的结论一样。导航实验中，陀螺简化模型引起的定位误差和加速度计简化模型二引起的定位误差与仿真得到的结论一致，但速度计简化模型一引起的定位误差远大于仿真得到的结果，主要原因是在导航实验中，不可避免的会存在转台定位误差、初始对准误差、算法误差和随机干扰等，这些都会对定位产生一定的影响。

4　结论

本文从IMU安装方式出发，建立IMU标定数学模型并对模型进行了两种简化处理，给出模型中各个参数的物理意义。针对陀螺和加速度计简化模型分别进行标定路径设计，并进行计算机仿真和统计特性分析。仿真及实验结果表明：简化的IMU标定数学模型引起捷联惯性导航系统速度误差、位置误差和姿态误差；在研究IMU标定原理和标定方式的同时，必须考虑IMU模型的精度和IMU模型对导航的影响。不同载体、不同精度、不同用途的IMU，其标定方式和数据处理方式也不尽相同，论文在进行仿真和导航实验时，只采用一种标定路径和数据处理方法进行探讨，对于采用其它标定方法时IMU简化模型对导航结果的影响，论文探讨不足。下一步的工作重点是探讨不同标定方法下IMU对导航系统的影响以及IMU非线性标定数学模型误差及其对导航系统的影响。

［1］Babichenko A V，Shkred V K.Main Errors of Inertial Navigation Systems［J］.Engineering Physics，2011，11（3）：34-53.

［2］魏莉莉，黄军，傅长松，等.带斜置元件的光纤陀螺捷联惯组标定方法［J］.中国惯性技术学报，2015，23（1）：14-19.

［3］朱战辉，汪立新，李灿.动态总方差及其在陀螺振动信号分析中的应用［J］.传感技术学报，2015，28（12）：1789-1794.

［4］林红斌，解静，王妍.基于正弦直线过载的惯组动态误差标定方法［J］.系统工程与电子技术，2013，35（10）：2152-2157.

［5］Syed Z F，Aggarwal P，Goodall C，et al.A New Multi-Position Cali⁃bration Method for MEMS Inertial Navigation Systems［J］.Mea⁃surement Science and Technology，2007，18：1897-1907.

［6］张斌，刘洁瑜，李成，等.抗差卡尔曼滤波在惯组外场自标定中的应用［J］.压电与声光，2013，35（5）：662-665.

［7］严恭敏，李四海，秦永元，等.惯性仪器测试与数据分析［M］.北京：国防工业出版社，2012.

［8］张慧，李杰，秦丽，等.基于GUI的MEMS大量程陀螺仪快速标定设计［J］.传感技术学报，2015，28（12）：1774-1778.

［9］MoonSik Kim，SiBok Yul，KwangSoo Lee.Development of a High-Precision Calibration Method for Inertial Measurement Unit［J］. International Journal of Precision Engineering and Manufacturing，2014，15（3）：567-575.

［10］程骏超，房建成，吴伟仁，等.一种激光陀螺惯性测量单元混合标定方法［J］.中国惯性技术学报，2014，22（4）：445-452.

［11］范建英，李杰，陈文蓉，等.高精度数字陀螺仪安装误差标定与补偿方法［J］.传感技术学报，2013，26（4）：525-529.

［12］赵桂玲，杨启航，李松.光纤陀螺标定误差对捷联惯导系统的影响［J］.辽宁工程技术大学学报，2014，33（12）：1635-1.

［13］赵剡，张少辰，胡涛.惯性测量组件离心机标定及误差分析方法［J］.北京理工大学学报，2015，35（4）：414-420.

［14］张红良，武元新，查亚兵，等.高精度惯测组合标定误差分析［J］.国防科技大学学报，2010，32（1）：142-146.

赵桂玲（1983-），女，博士，硕士生导师，河北吴桥人，主持国家自然科学基金一项，长期从事惯性导航和组合导航技术的研究，zhaoguiling0616@163.com；

姜雨含（1995-），女，辽宁沈阳人，辽宁工程技术大学测绘与地理科学学院学生，主持国家级大学生创新项目一项，长期从事惯性导航系统标定技术的研究，763005534@qq.com；

李松（1983-），男，河北吴桥人，博士研究生。长期从事数据通讯与信号处理研究，lgd_lisong@sina.cn。

EEACC：7230；7320E10.3969/j.issn.1004-1699.2016.06.016

IMU标定数学建模及误差分析*

赵桂玲*，姜雨含，李松
（辽宁工程技术大学测绘与地理科学学院，辽宁阜新123000）

惯性测量单元（IMU）标定路径设计和数据处理方法取决于IMU标定数学模型，安装误差是决定IMU标定模型的重要因素。针对工程中加速度计和陀螺相对载体安装方式的不同，提出一种通过坐标系转换矩阵建立IMU标定数学模型的方法，推导IMU标定模型误差与载体角速度和加速度之间的关系，分析IMU标定模型误差对捷联惯性导航系统导航参数的影响，并利用转台提供的位置信息设计IMU标定路径和数据处理方法。仿真和转台实验结果表明：IMU标定数学模型误差引起捷联惯性导航系统速度误差、位置误差和姿态误差；安装误差的表现形式决定了IMU标定模型误差对系统导航精度的影响。

惯性测量单元；标定；数学建模；安装误差；捷联惯性导航系统

TP212

A

1004-1699（2016）06-0886-06

2015-12-22修改日期：2016-03-01

项目来源：国家自然科学基金项目（41404035）；国家大学生创新训练项目（201510147000046）