Error Analysis and Calibration of MEMS Inertial Components*

YU Ting，SUN Wei，WEN Jian（School of Geomatics，Liaoning Technical University，Fuxin Liaoning 123000，China）



Error Analysis and Calibration of MEMS Inertial Components*

YU Ting，SUN Wei*，WEN Jian
（School of Geomatics，Liaoning Technical University，Fuxin Liaoning 123000，China）

In view of the influence of the working environment and the noise of the inertial sensor，the output signal noise ratio is low and the accuracy of the system is affected.The error analysis and calibration scheme of MEMS in⁃ertial device is proposed.MEMS output is identified by Allan variance method.The error term of data acquisition is obtained by curve fitting of output information.The error coefficients in the model are solved by using MEMS error model and tewnty-four position and speed calibration method.Experimental results of Turntable show that the meth⁃od of combining calibration based on position and rate can be used to extract the error coefficients of MEMS inertial device.The comparison results Verified that the error correction scheme is feasible.

MEMS；calibration；rate experiment；Allan variance；twenty-four position

MEMS惯性导航系统可为载体提供三维位置、速度及姿态信息［1］。但较低的信噪比限制了MEMS导航系统在众多领域中的应用。为降低器件误差对导航精度影响，开展MEMS误差特性分析、建模与误差修正方法研究成为在现有器件精度基础上实现更高精度导航的有效途径之一。Allan方差法由美国国家标准局的David Allan提出，是在时域上对频域稳定性进行分析的一种方法。它被广泛地用于分析产生噪声的随机过程的特性，并从数据中辨识出各种噪声［2-4］。该方法不仅适用于分析惯性器件的误差特性，而且也适用于任何精密仪器的噪声研究。论文基于上述方法对实验室自有MEMS惯性器件噪声误差进行评估，分解得到惯性器件随机误差主要成分；通过建立惯性器件几何数学模型并研究器件在已知条件下的漂移误差、标度因数及安装误差等误差项的标定分离方法，依据实验室三轴惯性测试转台开展位置与速率实验实现误差系数矩阵的求取。

1　MEMS惯性组件Allan方差分析

随机漂移率是衡量惯性器件性能的一项重要指标，但是它反映的是一个随机变化的过程，为开展MEMS惯性器件误差特性分析并实现误差参数的有效分离，通过绘制Allan标准差双对数曲线并进行曲线拟合实现MEMS器件的误差系数求取。

首先，设定系统采样时间为t，连续采样N个数据点并表示为Y（i）（i=1，2，3，…，N）。按照数据规范精度要求，将所采取数据分为K组，每组包含M个采样点（M≤（）N-1/2）。具体划分如图1所示［5-6］。

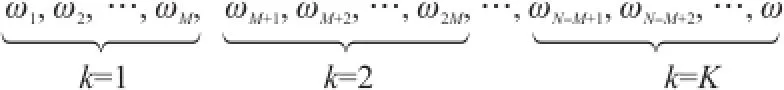
图1　Allan方差数据划分原理图

根据划分原理可知每组采样持续时间为τ=Mt，该时间成为采样过程中的相关事件，得到每组数据平均值可由式（1）获得。

基于上述操作过程，绘制MEMS惯性输出数据的Allan方差曲线，加速度计与陀螺仪对应的Allan方差曲线分别如图2和图3所示。

图2　MEMS加速度计Allan分析标准差与采样时间双对数曲线

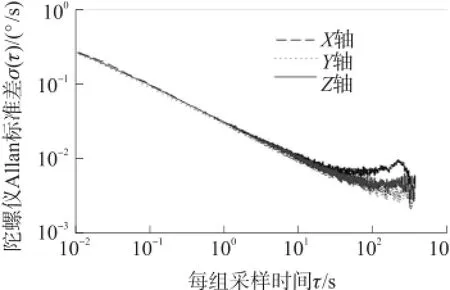
图3　MEMS陀螺仪Allan分析标准差与采样时间双对数曲线

以对Z轴方向陀螺仪的Allan标准差曲线为例进行分段分析。如图4所示，量化噪声对应的Allan标准差双对数曲线中-1斜率部分，角度随机游走对应斜率为-1/2的部分，零偏不稳定性对应于斜率为0的部分，速度随机游走对应斜率为1/2部分，速率斜坡对应斜率为1的部分。

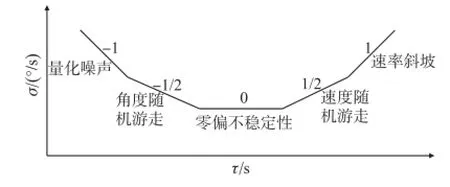
图4　MEMS惯性器件随机误差Allan标准差典型分布示意图

通过将平均时间小于0.5 s的部分数据拟合为斜率为-1的直线，直线与τ=3s处对应直线的交点即是量化噪声系数；将平均时间位于0.5 s至2 s的数据拟合成斜率为-1/2的直线，与τ=1 s处对应的直线交点即为角度随机游走系数；将平均时间大于20 s的平坦部分数据拟合为斜率为0的直线，与纵轴交点即为零偏稳定性系数，如图5所示。

图5　Z方向陀螺仪实测数据Allan方差分析结果

经过如上处理后得到的MEMS陀螺仪和加速度计的各项误差系数分别如表1和表2所示。

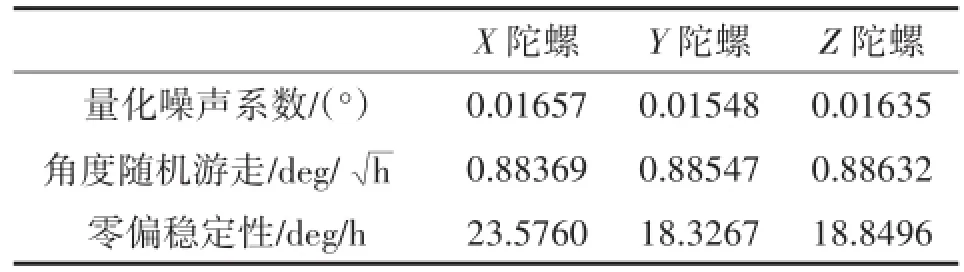
表1　MEMS陀螺仪各项误差分析结果

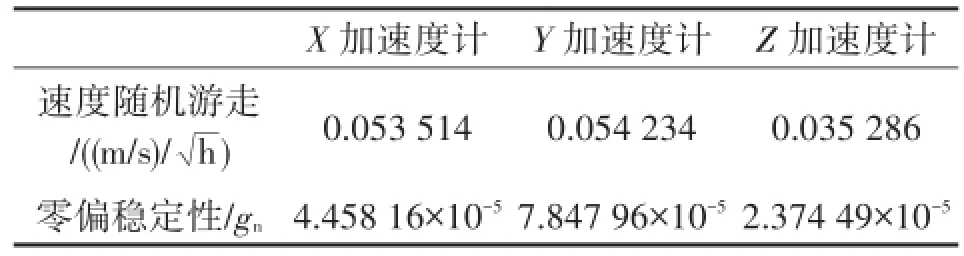
表2　MEMS加速度计各项误差分析结果

MEMS惯性器件的Allan方差符合限差要求，在此基础上根据最小二乘原理拟合误差曲线，获取MEMS惯性器件误差系数，为后续开展器件误差模型建立及误差参数的标定奠定基础。

2　误差建模

引起惯性器件产生误差的原因很多，既有惯性器件自身设计、装配工艺、工作机理等内在因素的影响，也有所附载体运动环境的恶劣和复杂性的影响［7-9］。对于采用三轴一体的惯性测量单元而言，惯性器件零偏、标度因数和安装误差等误差项混叠输出于载体真实运动信息中。因此，建立合理可行的惯性组件误差模型对于后续开展误差补偿尤为重要。

根据加速度计物理特性，建立包含零偏、标度因数及安装误差和二次项误差的加速度计误差数学模型［10-12］，如式（3）所示：

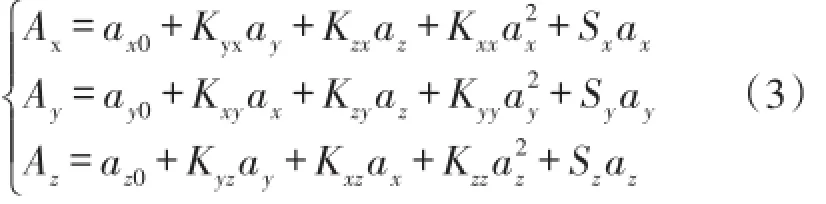
即：

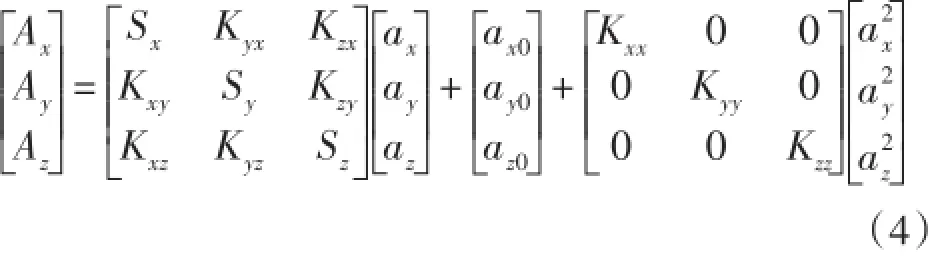
式中，Ai（i=x，y，z）为MEMS加速度计的实际测量值；ai0（i=x，y，z）为MEMS加速度计的零偏；Kij（i，j= x，y，z；i≠j）为MEMS加速度计安装误差系数；Si（i=x，y，z）为MEMS加速度计的刻度因数，Kij（i，j=x，y，z；i=j）表示二次项影响误差系数。

与加速度计模型类似，MEMS陀螺仪数学模型可定义为：

式中：Wi（i=x，y，z）为MEMS陀螺仪输出值；ωi0（i=x，y，z）为MEMS陀螺仪漂移；ωi（i=x，y，z）为MEMS陀螺仪输入值；Ski（i=x，y，z）为MEMS陀螺仪标定因数；Kij（i，j=x，y，z；i≠j）为MEMS陀螺仪安装误差系数。

3　标定方案设计与测试

3.1加速度计24位置标定

位置试验的目的是确定MEMS加速度计的标度因数、零位误差、安装误差、二次耦合项误差。其试验步骤如下：①捷联系统安装在转台的基座上，其X、Y、Z轴加速度计的主轴分别与转台的内、中、外框的自转轴平行；②按照图6所示的方位依次将X、Y、Z轴陀螺的主轴水平朝北；③每次加速度计主轴朝北时，绕该加速度计主轴将捷联系统按逆时针方向依次转动45°，连续转动7次，记录下每次加速度计的输出值。

图6　位置实验MEMS加速度计初始方位

试验中，为了避免转台启动和停止的影响，采样在转台完全静止后进行。每个加速度计主轴朝北时另外2个加速度计有8个不同的位置，整个试验包括24个位置的测试，所以该试验又称为“24位置静态试验”。

当以方位（a）为初始方位进行8个方位旋转时，陀螺和加速度计的输出值如下：

其中，φ1为以45°为间隔绕X轴旋转的角度，φ1=0～315 ，将（6）展开可得：

同理可得在方位（b）、（c）时，陀螺和加速度计的输出为：

由于加速度计误差模型为4项多项式，直接用代数运算比较繁琐，真正解算时需要对每个加速度计建立矩阵方程，现在建立X轴加速度计误差模型的矩阵形式：

式中，Ax（i）为X轴加速度计在上述24位置的输出信号平均值，ax（i）、ay（i）、az（i）为式（7）～（9）求出的基准值，式（10）可以化简为Z=AX+V的形式，根据最小二乘原理，待求量的估计值为=［AtA］-1AtZ，其中，=［SxKyxKzxax0Kxx］T。同理可建立Y、Z轴加速度计误差模型矩阵形式，然后求出误差系数得到如下计算结果：

3.2陀螺仪速率标定

MEMS陀螺标定方法是按照采用的速率标定需求，设置转台转动速度，转台正反两次转动，获取输出数据，对数据进行平均处理，将平均值作为陀螺仪输出，将转台提供的角速度及陀螺仪输出值代入数学模型中，获取数学模型中的误差系数完成陀螺仪误差项的标定。具体步骤如下：①将MEMS组建安装于测试转台几何中心，接通MEMS惯导系统电源并预热15 min；②设定转台工作路径，将转台绕方位轴正转，采集MEMS三轴方向上陀螺仪输出，完成后将转台反转，再次采集的MEMS三轴方向上陀螺仪输出；③设置采样时间以及所需的采样点数，求取特定输入角速率值下MEMS陀螺仪输出的平均值作为对应输入速率下的MEMS陀螺仪输出值；④围绕转台水平轴，重复过程②、过程③开展正反转速率实验，直至所需数据全部采集完毕，按照数学模型完成速率标定。

采集数据时根据实验及标定处理需求，按照速率为±40°、±63°、±100°分别采集X轴、Y轴、Z轴标定数据，选取每组数据平均值作为标定时陀螺仪输出，同时根据建立的标定模型，采用MATLAB编程计算出数学模型中各项系数。实验过程中采集的X、Y、Z轴标定时3个轴上陀螺仪输出数据的平均值分别如表3～表5所示。

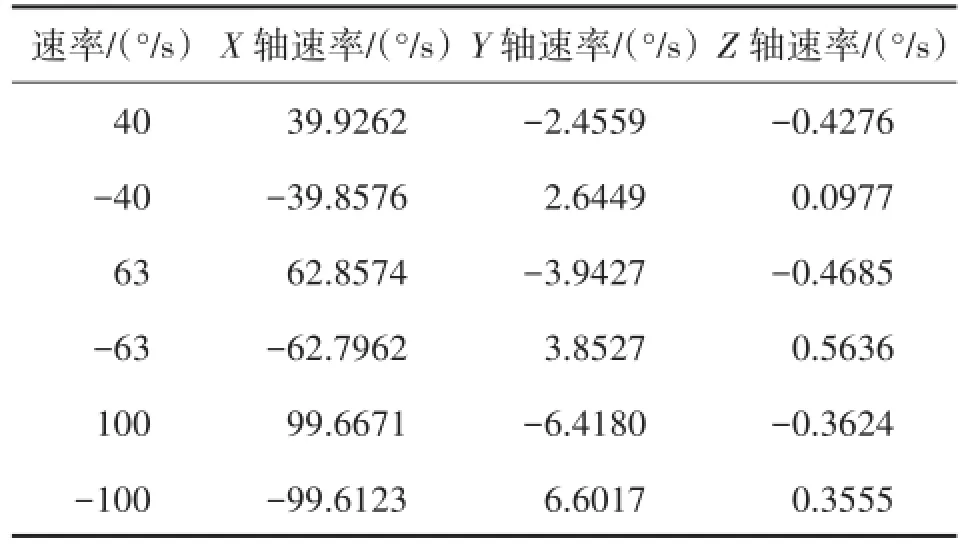
表3　X轴向标定时各轴陀螺仪输出平均值

表4　Y轴向标定时各轴陀螺仪输出平均值

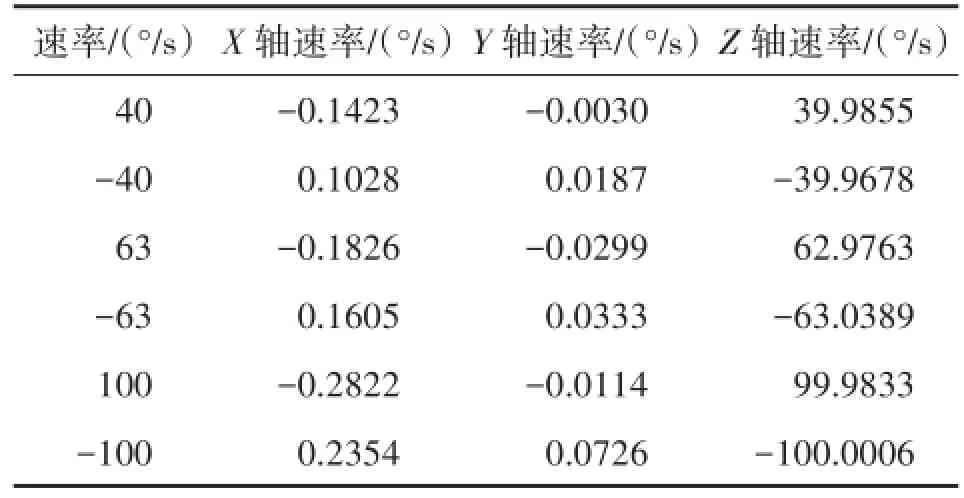
表5　Z轴向标定时各轴陀螺仪输出平均值

根据如上数据展开计算，得到MEMS陀螺仪误差模型如式（7）。

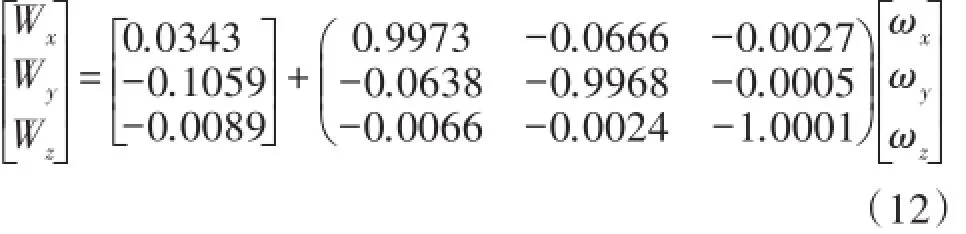
3.3测试结果及分析

利用加速度计和陀螺仪提供的加速度及角速率信息，对惯性组件误差参数进行辨识，将实验室现有MTI型惯性测量单元（如表6）固定于三轴惯性测试转台平面上，转台调平后保证器件坐标系与转台坐标系一致（如图7）。

将标定参数代入补偿模型，对陀螺仪及加速度计输出进行误差补偿。由于实验室转台已经进行过寻北，归零后所处的位置为实验所在位置的东北天导航坐标系。为验标定效果的优劣，分别将补偿前后的惯性器件输出值与转台提供的参考信息做差后观察误差曲线的分布情况。

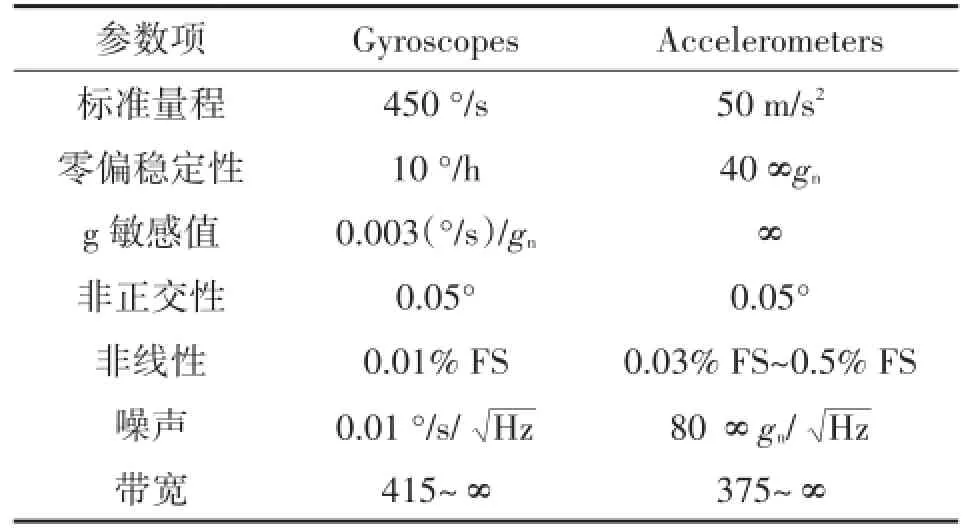
表6　MTI主要性能指标

图7　惯导测试三轴转台

如图8和图9所示，标定后的陀螺仪和加速度计输出值较为标定的原始输出相比，其精度均有提高。其中陀螺仪输出误差由原来的0.05°提升为0.01°；加速度计偏差也由为标定时候的0.5 gn提升到现在的0.01 gn左右，该标定结果可为今后开展惯性导航解算提供参考。

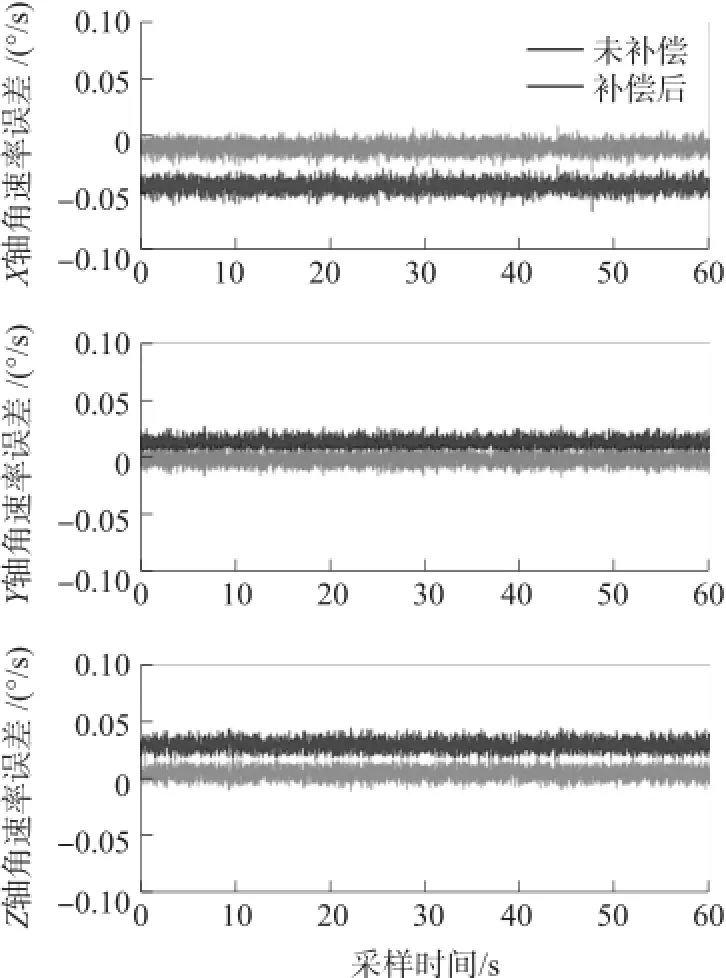
图8　陀螺仪补偿前后输出曲线

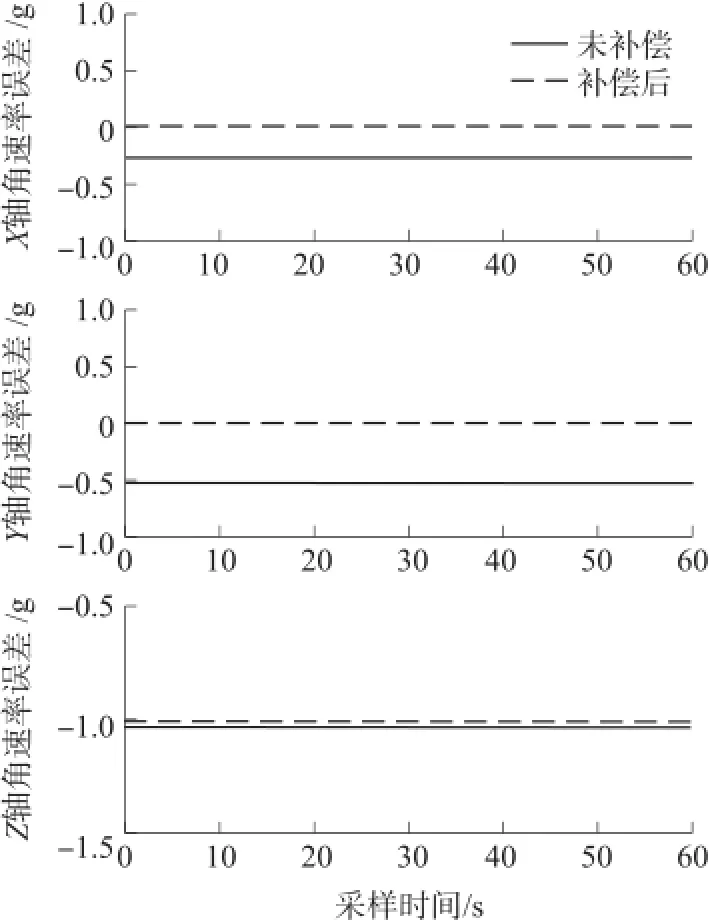
图9　加速度计补偿前后输出曲线

4　结语

惯性器件误差修正是当前在现有器件精度基础上提高导航精度的有效方法之一，论文采用Allan方差分析法对实验室现有MEMS传感器进行误差特性分析后，通过建立MEMS惯性器件误差模型并设计标定路径，设计了24位置的加速度计标定路径并提出速率标定方案实验对陀螺仪误差参数的计算求取。利用实验室现有三轴惯性测试转台搭建实验环境，分别以转台为参考基准，将标定前后的惯性器件输出与参考信息对比，得到标定后数据具有更准确描述载体运动转台的结论，该标定方法可为后续惯导解算提供技术支持。

［1］孙伟，李松，李瑞豹.带有转动机构的捷联惯导初始对准方法分析［J］.传感技术学报，2014，27（8）：1082-1087.

Sun Wei，Li Song，Li Ruibao.Analysis of the Initial Alignment of Rotary Fiber Inertial Navigation System［J］.Chinese Journal of Sensors and Actuators，2014，27（8）：1082-1087.

［2］赵思浩，陆明泉，冯振明.基于一种简化Allan方差法的IMU误差分析［J］.传感器与微系统.2010，29（12）：12-14.

Zhao Sihao，Lu Mingquan，Feng Zhenming.IMU Error Analysis Based on a Simplified Allan Variance Method［J］.Sensor and Mi⁃cro System，2010，29（12）：12-14.

［3］高宗余，方建军，于丽杰.MEMS传感器随机误差Allan方差分析［J］.仪器仪表学报，2011，32（12）：2863-2868.

Gao Zongyu，Fang Jianjun，Yu Lijie.Allan Variance Analysis of Random Error of MEMS Sensor［J］.Chinese Journal of Scientific Instrument，2011，32（12）：2863-2868.

［4］张亚宁，朱涛，傅军.基于Allan方差的MEMS陀螺误差分析［J］.自动化与仪器仪表，2013（3）：157-158.

Zhang Yaning，Zhu Tao，Fu Jun.Error Analysis of MEMS Gyro⁃scope Based on Allan Variance［J］.Automation and Instrumenta⁃tion，2013（3）：157-158.

［5］宋海滨，杨平，徐立波.MEMS传感器随机误差分析与处理［J］.传感技术学报，2013，26（12）：1719-1723.

Song Haibin，Yang Ping，Xu Libo.Random Error Analysis and Processing of MEMS Sensor［J］.Chinese Journal of Sensors and Actuators，2013，26（12）：1719-1723.

［6］孙枫，曹通.基于Kalman滤波的加速度计十位置标定方法［J］.系统工程与电子技术，2011，33（10）：2272-2276.

Sun Feng，Cao Tong.Ten Position Calibration Method of Acceler⁃ometer Based on Kalman Filter［J］.System Engineering and Elec⁃tronic Technology，2011，33（10）：2272-2276.

［7］田晓春，李杰，范玉宝，等.一种微惯性测量单元标定补偿方法［J］.传感技术学报，2012，25（10）：1411-1415.

Tian Xiaochun，Li Jie，Fan Yubao，et al.Calibration Method for Micro Inertial Measurement Unit［J］.Chinese Journal of Sensors and Actuators，2012，25（10）：1411-1415.

［8］宋丽君，秦永元.MEMS陀螺仪的一种实用标定方法［J］.压电与声光，2010，32（3）：372-374.

Song Lijun，Qin Yongyuan.A Practical Calibration Method for MEMS Gyroscope［J］.Piezoelectric and Sound，2010，32（3）：372-374.

［9］宋丽君，秦永元.MEMS加速度计的六位置测试法［J］.测控技术，2009，28（7）：11-13.

Song Lijun，Qin Yongyuan.Six Position Testing Method for MEMS Accelerometer［J］.Measurement and Control Technology，2009， 28（7）：11-13.

［10］Minha Park，Yang Gao.Error Analysis and Stochastic Modeling of Low-Cost MEMS Accelerometer［J］.Journal of Intell Robot Sys⁃tem.2006，46：27-41.

［11］Sun Wei，Gao Yang.Fiber-Based Rotary Strapdown Inertial Navi⁃gation System［J］.Optical Engineering，2013，52（7）：1-12.

［12］Heckman D W，Baretela M.Interferometric Fiber Optic Gyro Technology［J］.IEEE Aerospace and Electronic Systems Maga⁃zine，2000，15（2）：23-28.

于婷（1991-）女，辽宁省葫芦岛人。现为辽宁工程技术大学测绘与地理科学学院硕士研究生。长期从事惯性数据处理方法研究；

孙伟（1984-）男，教授，博士生导师，，黑龙江萝北县人。2007年于哈尔滨工程大学获得学士学位，2011年于哈尔滨工程大学获得博士学位。主持国家级、省部级科研项目7项；发表学术论文四十余篇，其中SCI论文6篇，EI论文20篇。长期从事惯性导航技术研究，sunwei-3775235@163.com。

EEACC：723010.3969/j.issn.1004-1699.2016.06.012

MEMS惯性组件的误差特性分析与标定*

于婷，孙伟*，文剑
（辽宁工程技术大学测绘与地理科学学院，辽宁阜新123000）

针对惯性器件输出受工作环境及器件自身噪声影响，导致惯性组件输出信噪比低进而影响系统定位测姿精度等问题，提出MEMS惯性组件误差分析与标定方案。利用Allan方差对MEMS输出进行辨识，对输出信息曲线拟合并确立MEMS器件误差项的误差取值，建立MEMS几何误差模型并设计分立式标定方案。转台实验结果表明，24位置及速率标定方法可实现惯性组件常值误差系数的有效分离与求取，对比器件误差补偿前后的结果，验证了误差修正方案的可行性。

MEMS；标定；速率实验；艾伦方差；24位置

TP 212

A

1004-1699（2016）06-0859-06

2015-11-04修改日期：2016-02-29

项目来源：国家自然科学基金项目（41304032）；高等学校博士学科专项科研基金（新教师类）项目（20132121120005）；第8批中国博士后科学基金特别项目（2015T80265）；第58批中国博士后科学基金面上项目（2015M581360）；辽宁省高等学校杰出青年学者成长计划项目（LJQ2015044）；辽宁省“百千万人才工程”培养经费项目（辽百千万立项［2015］76号）；辽宁省自然科学基金项目（2015020078）；江西省数字国土重点实验室开放研究基金项目（DLLJ201501）；精密工程与工业测量国家测绘地理信息局重点实验室开放基金项目（PF2015-13）；地球空间环境与大地测量教育部重点实验室开放基金项目（14-01-05）；对地观测技术国家测绘地理信息局重点实验室基金项目（K201401）；海岛（礁）测绘技术国家测绘地理信息局重点实验室项目（2014B05）