Forecasting of MEMS Gyroscope’s Random Drifts Based on LSSVM Optimized by Modified PSO

SUN Tianchuan，LIU Jieyu*，KANG Li，YANG Haotian（.Dept of Control Engineering，The Second Artillery Engineering University，Xi’an 7005，China；.The Second Research Institute of CASIC，Beijing 00039，China）



Forecasting of MEMS Gyroscope’s Random Drifts Based on LSSVM Optimized by Modified PSO

SUN Tianchuan1，LIU Jieyu1*，KANG Li2，YANG Haotian1
（1.Dept of Control Engineering，The Second Artillery Engineering University，Xi’an 710025，China；2.The Second Research Institute of CASIC，Beijing 100039，China）

The predictive-modeling method for the random drift of MEMS gyroscope is proposed，which is based on the least squares support vector machine optimized by modified particle swarm algorithm.Firstly，a forecasting mod⁃el of the random drift of MEMS gyroscope is built with least squares support vector machine，and then，the modified particle swarm algorithm is put forward to optimize the model.Finally，the optimized LSSVM model is used to pre⁃dict the random drift of MEMS gyroscope.The modeling method solves SVM’s disadvantage of slow training speed and requesting more resources.What’s more，the modified PSO have better fitness in capability of global searching or local searching.The experimental result also shows that the new modeling method can effectively predict MEMS gyroscope’s random drifts，and it has better effect than LSSVM optimized by PSO.

mems gyroscope；least squares support vector machine；modified particle swarm algorithm；random drift

MEMS陀螺仪具有成本低、体积小、功耗低、抗冲击能力强等优点，近年来得到了快速的发展［1］，然而由于存在较大的漂移，尤其是具有随机性、非线性、非平稳性和弱时变性的随机漂移，限制了它在很多领域的应用［2-3］。因而，对MEMS陀螺的随机漂移进行预测和补偿一直是研究的重要方向［4］。

最小二乘支持向量机（LS-SVM）是最早是由Suykens J.A.K.在1999年提出的，是标准支持向量机的一种扩展，它把优化问题转化成解线性方程问题而非二次规划问题，这使得它在需要较少的计算资源的同时，还能较快的求解。文献［5］将LSSVM用于加速度计温度建模和补偿，取得了较好的效果，文献［6］将LSSVM和小波结合并用于陀螺仪随机漂移建模中，为随机漂移处理提供了一个新的思路。

然而LSSVM的参数γ和σ2会较大地影响到它的预测精度［7］，通常采用参数空间穷尽搜索法对LSSVM的参数进行优化［8］，但使用这种优化方法，参数范围很难确定。因此，本文采用一种基于改进惯性权值非线性递减策略的粒子群算法优化LSSVM的参数，提高了LSSVM的预测精度，实验结果也表明，该算法预测效果优于基本PSO优化下的LSSVM。

1　最小二乘支持向量机（LSSVM）

LSSVM是标准支持向量机的一种扩展。其选择误差变量ei的二范数为损失函数，并把优化问题转化成解线性方程问题而非二次规划问题，约束条件也变为等式约束而非不等式约束。因为采取了求解线性方程的方式，所以当数据量较大时，需要的计算资源较少，且求解和收敛的速度比较快［9］。LSSVM的算法如下：

①假设已知训练集

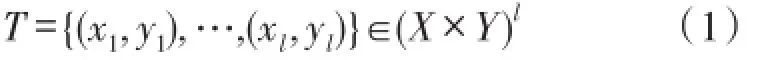
其中，xi∈X=Rn，yi∈R为训练样本输出；

②选择适当的参数和适当的核函数；核函数是支持向量机的重要组成部分，具有不同核函数和参数的支持向量机的性能存在很大差异。所以如何根据数据集来构造核函数，通过构造该函数来提高支持向量机的分类能力，这是目前支持向量机技术发展的一个重要研究方向。

根据泛函的相关理论只要满足Mercer条件的函数都可以作为支持向量机的核函数，这里选用径向基核函数：

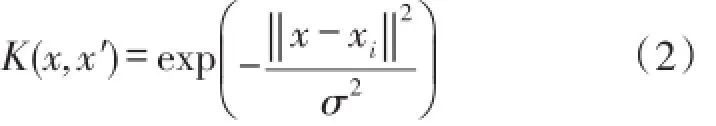
主要考虑到采用径向基核函数的LS-SVM只需要确定参数γ和σ。

③根据统计学习理论，为了使得训练集中的任意数据点向量离超平面最短距离最大的最优超平面，构造函数拟合问题，LS-SVM算法的目标优化函数为：

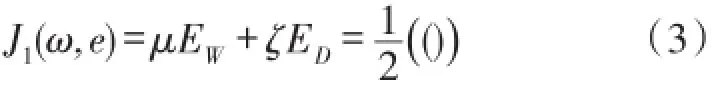
约束条件为：

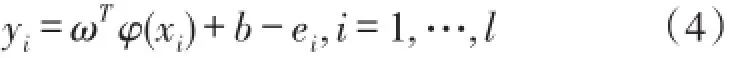
其中，φ（）：Rn→Rnh为核空间映射函数，ω∈Rnh为权向量，e=（e1，…，el）T为误差变量，b为偏差量，J1为损失函数，μ和ζ为可调参数。

为了求解目标优化函数的最小值，将（3）和（4）变换到对偶空间，并构造相应的拉格朗日函数：

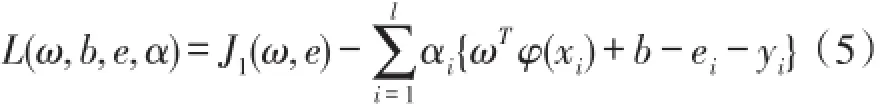
式中，αi∈R为拉格朗日乘子，分别求上式对ei，αi，ω，b的偏导，

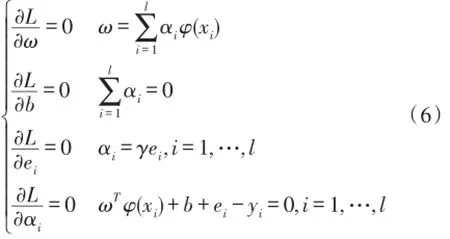
再消去ei，ω，得到方程：

构造LS-SVM模型的预测函数：

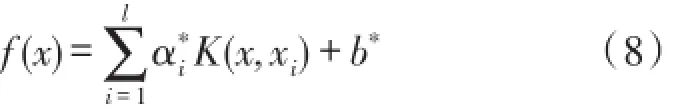
即为超平面判别函数，其中K（x，xi）=ϕ（x）Tϕ（xi）就是核函数部分。

由以上推导过程可以看出，这种把求解的优化问题转化成线性方程的方式，将算法的复杂性大大地降低了。

2　基于改进粒子群优化的的最小二乘支持向量机

在LSSVM的回归模型中，惩罚参数γ和核参数σ2对其性能影响最大。使用粒子群优化算法对这两个参数进行选择可以有效提高最小二乘支持向量机的预测性能［10］，而PSO算法由于采用线性递减权重策略，在局部搜索和全局搜索的侧重上存在缺陷；所以本文提出一种基于新的非线性惯性权值的自适应粒子群算法对这两个参数进行优化，从而提高文中模型的预测精度。

2.1粒子群优化算法及其改进

粒子群算法是一种从鸟类捕食行为衍生出来的群智能寻优算法，它通过对一群随机粒子的初始化和迭代来寻找最优解。Pi是第i个粒子经历过的最优位置，Pg是群体经历的最优位置，在每一次的迭代中，粒子通过寻找个体极值Pi和全局极值Pg来更新自己的速度和位置；假设在d维搜索空间中，有m个粒子组成一个群体，第i个粒子在d维空间中的位置表示为X¯i=（xi1，xi2，…，xid），i=1，2，…，m，第i个粒子经历过的最好位置（有最好适应度）记为P¯i=（pi1，pi2，…，pid），i=1，2，…，m，每个粒子的飞行速度为V¯i=（vi1，vi2，…，vid），i=1，2，…，m。在整个群体中，所有粒子经历过的最好位置为P¯g=（pg1，pg2，…，pgd），每一代粒子根据下面公式更新自己的速度和位置：

其中，w为惯性权重；c1，c2为学习因子，一般取值为2；r1，r2是［0，1］之间的随机数。

参数w是其中最为重要的一个参数，因此选择合适的w可以使算法搜索行为和性能更好。w较大则算法具有较强的全局收敛能力，有利于跳出局部极小点，而w较小，算法则具有较强的局部收敛能力，有利于算法的收敛。所以惯性权重应该随着迭代次数的增加不断减小来使PSO在初期全局收敛能力较强，而晚期局部收敛能力较强［11］。目前主要采用的权值调整策略是线性递减权重（linearly decreasing weight）策略，随着迭代的进行，w的值会线性减少，这种递减策略描述如下：

其中，Tmax是最大允许迭代次数，wini为是初始的惯性权重，而wend则是进化到最大迭代次数时的惯性权重，通常取wini=0.9，wend=0.4［12］。

为了使得算法在迭代初期探索能力更强，在可能最优解周围实施更加精细的搜索。本文提出一种新的非线性递减惯性权值策略。w（t）如下所示：

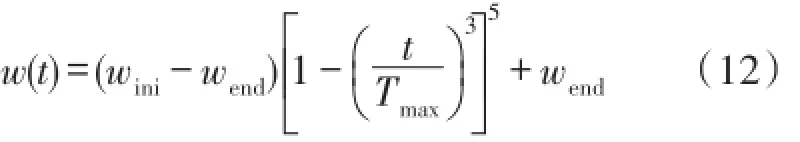
式中，t为当前迭代次数，Tmax为最大允许迭代次数。此种方法和传统方法的惯性权重变化曲线如图1所示（假设Tmax=1 000）。

图1　不同策略惯性权重变化曲线

如图1中所示，点划线描述的曲线为线性递减权重，蓝色实线为本文使用的非线性惯性权重递减变化曲线。这里通过采用本文提出的惯性权重非线性递减策略与线性递减策略对比的方式，可以发现本文的递减策略使得算法在迭代初期具有更强的全局搜索能力来不断搜索新的区域，迭代后期则具有更强的开发能力也就是局部搜索能力，使之在可能最优解周围实施更加精细的搜索。

2.2改进的粒子群算法优化LSSVM过程

通过上述基本知识的描述，改进的粒子群算法优化最小二乘支持向量机的一般步骤如下：

①粒子群算法参数的初始化

首先确定最小二乘支持向量机的惩罚参数γ和核参数σ2范围，文中设定γ∈［0，1 000］，σ2∈［0，100］；其次确定改进粒子群算法的相关参数，这些参数包括：粒子数目40，学习因子c1=c2=2，最大迭代次数tm=1 000。然后在最小二乘支持向量机的惩罚参数γ和核参数σ2范围内随机初始化粒子群。

②根据式（12）计算自适应权重。

③以回归误差平方和最小为适应度，计算并比较适应度。记录各粒子的最佳位置和全局最佳位置。

④根据式（9）、式（10）更新粒子的速度和位置。

⑤判断终止条件，满足条件则输出结果，否则转向步骤②。

3　实验验证

3.1数据来源

采集一组MEMS陀螺仪ADXRS300的静态数据，并经过确定性误差补偿和小波阈值去噪，得到陀螺仪随机漂移的时间序列。取该时间序列中长度为3 600的一段序列作为实验数据，原始随机漂移变化曲线如图2所示。取前2 500个样本点作为训练集训练模型，选择参数。取后500个样本点做测试验证模型预测性能。

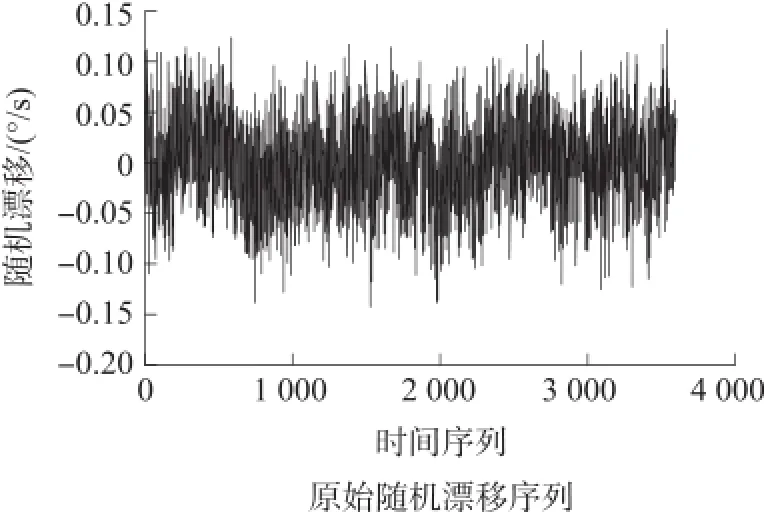
图2　原始随机漂移序列

3.2模型评价指标

为了比较本文预测方法的预测性能，我们采用基本粒子群算法优化LSSVM对数据进行预测，并将它的预测结果和本文方法作为对比。模型评价指标则选择均方根误差（RMSE）和平均绝对百分误差（MAPE）。

3.3模型参数的确定

基于10折交叉验证的最小预测误差准则，采用基本粒子群算法和改进的自适应粒子群算法对LSSVM的参数（γ，σ2）进行优化，参数的具体值如表1所示。

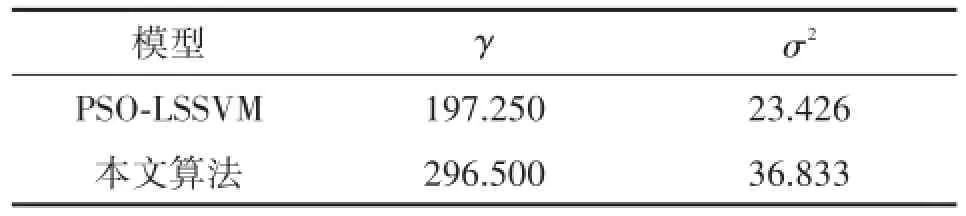
表1　各模型的参数

3.4结果与分析

①拟合性能对比采用表1中的LSSVM参数建立相应的MEMS陀螺随机漂移预测模型，各模型拟合结果及拟合误差如图3、图4所示。计算这两个模型拟合结果的RMSE和MAPE值，结果见表2所示，从表2可知，相对于PSO-LSSVM，本文的基于改进PSO算法优化的LSSVM可以获得更高的拟合精度，拟合误差更小。

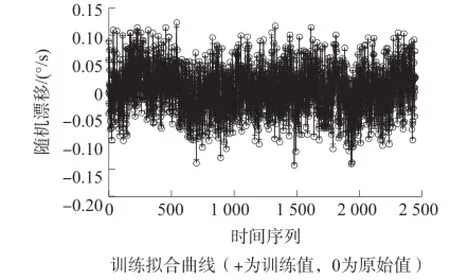
图3　PSO-LSSVM训练拟合效果图

图4　改进PSO-LSSVM训练拟合效果图

表2　各模型拟合性能比较

对比结果表明，改进PSO算法可以找到更优的LSSVM参数，建立了整体性能更优的MEMS陀螺随机漂移预测模型，获得更好的拟合效果。

②预测能力对比

模型的预测结果与预测误差变化曲线如图5和图6所示。预测结果的RMSE和MAPE见表3所示。对结果进行分析，可以得到如下结论：相对于基本PSO-LSSVM，本文的改进PSO优化LSSVM对MEMS陀螺随机漂移的预测结果更加理想，这是由于基本PSO算法优化LSSVM参数时，易陷入局部最优，未能搜索到使模型整体性能最优的参数，而改进的PSO算法由于采用改进的非线性惯性权重递减策略，可以获得更优的模型参数，使随机漂移预测模型的预测能力更强，可以更加准确反映MEMS陀螺随机漂移的变化趋势。

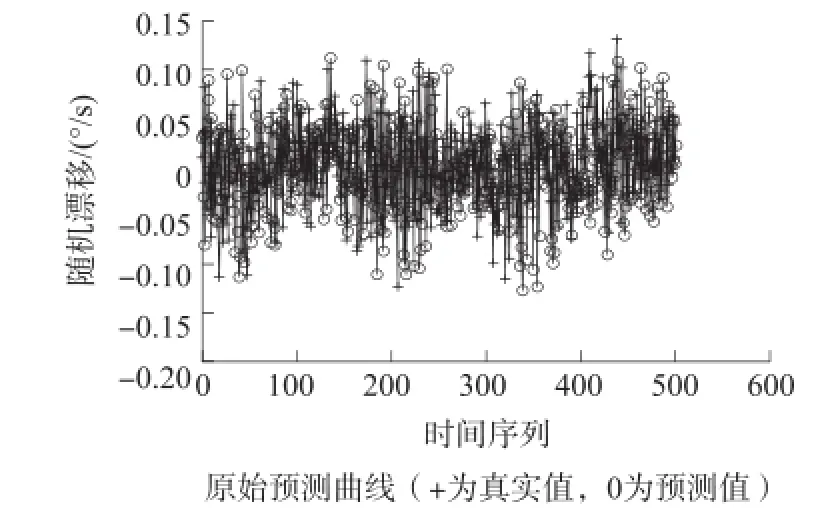
图5　PSO-LSSVM预测效果图

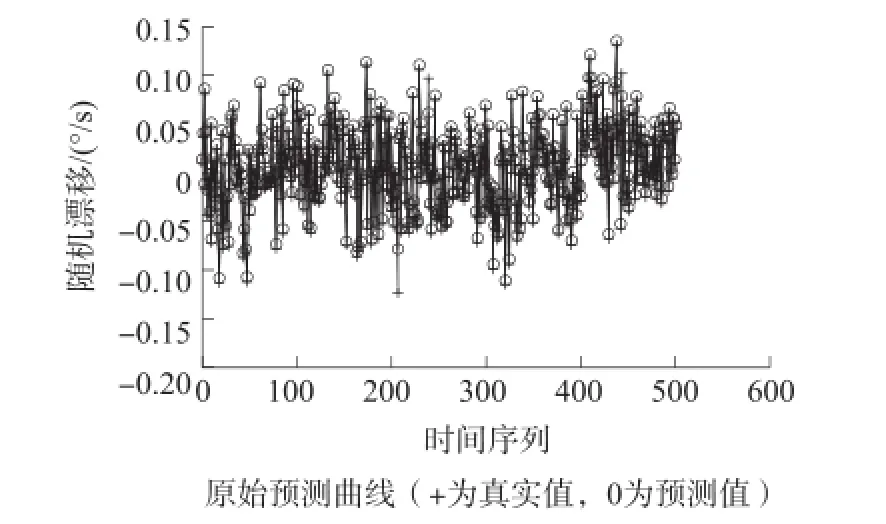
图6　改进PSO-LSSVM预测效果图

表3　各模型预测性能比较

4　结束语

针对LSSVM参数优化问题，提出一种基于改进PSO优化的LSSVM的MEMS陀螺随机漂移预测模型。该模型通过采用改进的惯性权重非线性递减策略，相较于线性递减策略，算法在迭代初期w较大，全局搜索能力较强，可以不断搜索新的区域，迭代后期w较小，局部搜索能力较强，使得算法在可能最优解周围可以实施更加精细的搜索从而选择更合理的模型参数提高模型预测性能。通过对比基本PSO优化LSSVM的预测效果，可以发现此方法预测能力更强。

［1］Barbour N，Connelly J，Gilmore J，et al.Micromechanical Silicon Instrument and System DevelopmentatDraperLaboratory［C］//AIAA Guidance Navigation and Control Conference.San Di⁃ego：AIAA，1996：1-7.

［2］陈旭光，杨平，陈意.MEMS陀螺仪零位误差分析与处理［J］.传感技术学报，2012，25（5）：628-632.

［3］王新龙，李娜.MEMS陀螺仪随机误差的建模与分析［J］.北京航空航天大学学报，2012，38（2）：170-172.

［4］李泽民，段凤阳，马佳智.基于支持向量机的MEMS陀螺仪随机漂移补偿［J］.传感技术学报，2012，25（8）：1085-1087.

［5］于湘涛，张兰.基于小波最小二乘支持向量机的加速度计温度建模和补偿［J］.中国惯性技术学报，2011，19（1）：95-98.

［6］Yang P X，Qin Y Y.Temperature Compensation for RLG Based on Neural Network［C］//Sixth International Symposium on Preci⁃sion Engineering Measurements and Instrumentation，2010，7544：（4J-1-7）.

［7］黄翀鹏，熊伟丽.PSO算法中惯性权值的非线性递减策略研究［C］//中国控制与决策学术年会论文集：481-484.

［8］陈贵敏，贾建援，韩琪.粒子群优化算法的惯性权值递减策略研究［J］.西安交通大学学报，2006，1（40）：53-56.

［9］安凤栓，常俊林.基于改进粒子群优化算法的PID控制器参数优化［J］.工矿自动化，2010（5）：54-57.

［10］Silva C G.Time Series forecasting with a Nonlinear Model and the Scatter Search Meta-Heuristic［J］.Information Sciences，2008，178（16）：3288-3299.

［11］He Jieyue，Hu Haejin，Robert Harrison，et al.Rule Generation for Protein SecondaryStructurePredication withSVMand De⁃cision Tree［J］.IEEE Transactions on Nanobioscience，2006，5（1）：46-53.

［12］田东平，赵天绪.基于Sigmoid惯性权值的自适应粒子群优化算法［J］.计算机应用，2008，28（12）：3058-3060.

孙田川（1993-），男，汉族，湖北人，硕士研究生，仪器科学与技术专业，主要研究方向为MEMS陀螺仪误差补偿技术研究，405528554@qq.com；

刘洁瑜（1970-），女，汉族，陕西西安人，博士学位，教授，硕士生导师，主要研究方向为惯性仪表及导航技术，主持并参与了多项军内重要科研项目，多次获得各级军队科技进步奖，jieyu.liu@gmail.com。

EEACC：2575；722010.3969/j.issn.1004-1699.2016.06.011

基于改进PSO优化LSSVM的MEMS陀螺随机漂移预测

孙田川1，刘洁瑜1*，康莉2，杨浩天1
（1.第二炮兵工程大学控制工程系，西安710025；2.二炮驻699厂军代室，北京100039）

提出一种基于改进粒子群算法（PSO）优化最小二乘支持向量机（LSSVM）的MEMS陀螺随机漂移的预测模型建立方法。该方法首先应用最小二乘支持向量机对MEMS陀螺随机漂移建立预测模型，然后应用改进粒子群算法对该模型进行优化，最后应用参数优化后的LSSVM预测模型对随机漂移进行预测。该方法不仅解决了支持向量机训练速度慢和所需计算资源多的问题，而且文中提出的改进的惯性权值递减策略使PSO算法在全局或局部搜索能力上的侧重具有更好的适应度。实验结果表明，该预测模型可以有效地进行陀螺随机漂移的预测，且预测效果优于基本PSO优化的最小二乘支持向量机。

微机械陀螺仪；最小二乘支持向量机；改进粒子群优化算法；随机漂移

V241.5

A

1004-1699（2016）06-0854-05

2015-12-08修改日期：2016-02-27