A Grating Signal Segmentation Method Based on FPGA*

XU Ding，LI Binhua，YANG Xiaohan（Faculty of Information Engineering and Automation，Kunming University of Science and Technology，Kunming 650500，China）



A Grating Signal Segmentation Method Based on FPGA*

XU Ding，LI Binhua*，YANG Xiaohan
（Faculty of Information Engineering and Automation，Kunming University of Science and Technology，Kunming 650500，China）

A grating signal segmentation and the direction based on FPGA are adopted in the high precision mea⁃surement，in order to improve the accuracy of the grating segmentation.Firstly，Matlab is used for analysis two origi⁃nal signals and filtered and the filtered DC component of the signal characteristics output from the read head.The feasibility of 1024 subdivision algorithm implementation and hardware circuit are verified，according to structure subdivision algorithm，the grating signal is subdivided and identified direction.Tessellation hardware circuit is di⁃vided into 8 sub-division circuit.Which is 8 segmentation in each cycle of one main signal.Mainly，the accurate cir⁃cuit handles the eight cycle of each signal segment.The results of the test show that the subdivision circuit achieve the 1024 subdivision of the grating，and the high-powered subdivision purpose.

FPGA；grating signal；measurement；subdivision；identify the direction

光栅在自动化测量、高档数控机床及精密加工等领域应用十分广泛。不管是增量式光栅还是绝对式光栅，要达到高精度和高分辨率的测量，通常都需要对光栅的原始正交信号进行整形并对其细分。国内外学者对光栅的细分技术进行了大量的研究，涉及的技术面也很广，方法种类很多，比如光学细分法、电子学细分法和微处理器软件细分法等几大类［1］。光学细分法由于受到制造工艺限制，细分倍数很难提高。电子学细分法和微处理器软件细分法有着细分倍数较高、电路简单、跟踪速度快等特点，调节方便，容易实现数字化测量和智能化控制，因而被广泛运用。但由于受到光栅间隙、衍射、光源、温度以及制造工艺等限制，光栅输出信号含有电平漂移、正弦和余弦信号幅度差太大、正交性等现象，这些因素会影响现有细分方法的精度及可靠性［2］。因为现有细分方法的基础是光栅输出为纯净的标准正弦波信号，所以细分前要尽可能消除上述不良因素的影响。

但是，在生产制造过程中，完全消除上述影响的可能性是不大的。因此，为进行高倍细分，还需要对光栅信号进行补偿和修正［3］。对编码器输出的原始信号，在前端读数头及其后端的细分盒中都需要进行修正［4-5］。根据修正之后波形的特点，提出了一些有针对性的细分方法，其中应用最多的是电子学细分法，每种细分方法都有优缺点。刘世峰［6］使用幅值采样的方法，其硬件结构没有对信号滤波处理，且采用单片机（MCU）作为主处理器，其细分速度和精度受到很大影响。喻洪麟等人［7］采用数字信号处理器（DSP）对光栅信号进行数字滤波，采用合成函数细分与幅值相结合的方法，在几微秒的时间内对光栅做到了500细分，但是当细分倍数高时，其所用的存储单元会使细分速度受到很大影响。曹永刚［8］采用纯硬件对编码器进行细分，通过查找地址完成了对光栅信号一个周期256细分，但是其做到高倍细分受到其硬件结构的高位模数转换器（ADC）和大容量存储器限制。

为了节省信号细分的软件处理时间，提高信号处理速度，本文采用纯硬件实现对信号的细分。文中首先分析了雷尼绍读数头输出的光栅信号、滤波后的信号，据此构造了相应的细分算法，然后设计并制作了基于现场可编程门阵列（FPGA）的细分电路，实现了对光栅信号的1024细分和辨向计数。

1　光栅信号的分析与预处理

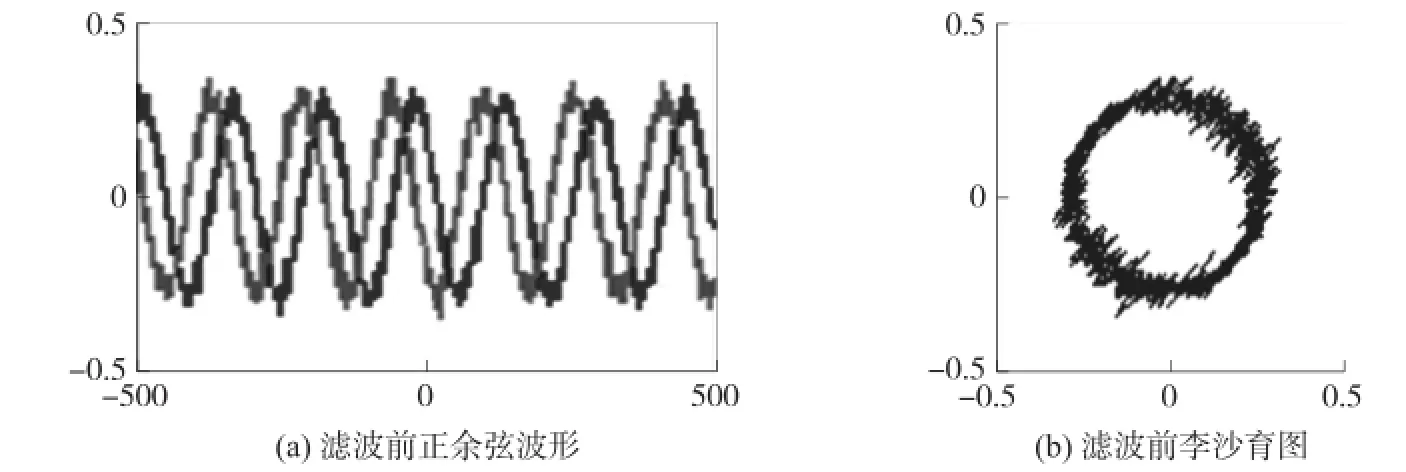
图1　采集到的实际信号

为设计有效的细分算法和实现电路，必须了解光栅信号的特点。为此，我们先对雷尼绍读数头SR050A输出的光栅信号进行采集、分析和预处理。

1.1光栅信号的采集与复现

雷尼绍读数头SR050A输出四路相差90°的正余弦信号，用示波器观察这些信号，发现其中噪声很大。我们使用安捷伦6000系列示波器将光栅信号保存为csv格式的数据。图1（a）为这两个信号滤波前的波形，图1（b）为这两个信号的李沙育图。差分运算的两个输入信号的相位差为180°，经差分运算后输出的信号直流电平和偶次谐波均减小，同时奇次谐波增加了近一倍。从图中可以看出，差分后的信号大致是一个正余弦信号，且含有明显的高频噪声，后续使用时必须滤波处理。从统计分析表明，这两个正余弦信号直流偏量分别为-0.012 7和0.003 9，说明这两个信号中含有少量直流成份。

将差分信号的数据保存为csv格式数据，导入到安捷伦可编程函数信号发生器33250A，就可以将差分后的光栅信号，通过该信号发生器复制并输出。这对后续细分算法的设计、滤波与细分硬件电路的设计、调试是很重要的。

1.2光栅信号正弦属性分析

原始光栅出来的信号是一个类似正弦波的信号，经过读数头输出信号和原始信号可能有所差别。高倍细分要求信号是正余弦信号，为此，需要分析实测的光栅信号是否是正余弦信号。

由于实测光栅差分信号有明显的噪声，根据采集的一段信号的频率是1.3 kHz和采样频率是200 kHz。由于实际运动不是匀速运动，信号的最高频率略大于1.3 kHz，为此我们设计截止频率是4 kHz的FIR滤波器对其滤波，去除高频噪声，获得如图2中实线所示的滤波后并滤除直流分量的光栅信号。然后，用安捷伦6000系列示波器将滤波后的光栅信号的数据进行采集、保存。再以此数据拟合出一个标准的正弦函数，得到波形如图2虚线所示。利用统计学回归分析理论的曲线相关系数R2对所建立的模型进行拟合度检验。曲线相关系数R2定义如下：

式中，YRSS=∑（yi-y̑i）2，是残方差平方和；YTSS=∑（yi-y¯i）2，是总平方和。这里yi为一系列标准数学正弦函数的值，y̑i为一系列采集到的读数头滤波之后数据。R2（0≤R2≤1）反映了在实际采集的数据y的总变异由标准函数之间的比例或百分比［9］。

使用Matlab进行数据处理，拟合度计算结果为99.81%，说明拟合度接近于1，说明实测光栅信号非常接近标准的正弦函数。因此，读数头的光栅信号类似正弦波，可见读数头已经对光栅信号做了初步处理。

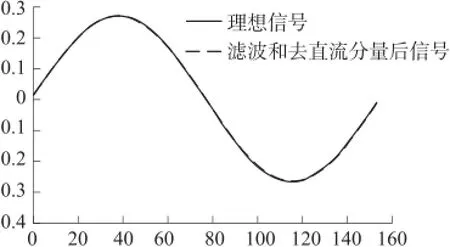
图2　滤波去直流分量数据与理想数据拟合

1.3光栅信号的正交性、幅值和直流分量偏差的分析

FIR低通滤波器对原始光栅信号进行数字滤波之后，然后绘制李沙育图像如图3所示。其中图3（a）为两路光栅正余弦信号，图3（b）中实线是用这两个光栅信号绘制的李沙育图，为了便于比较，用虚线绘制了一个标准圆。该图3与图1比较，显然高频噪声基本被滤除了，说明所涉及的FIR低通滤波器是有效的。

从图3（b）图可以看出，李沙育图基本上是一个正圆，但与标准的圆心有点偏移，这是说明光栅差分信号中仍然存在微小的直流分量，使信号的直流电平偏离预定值，从而造成相位圆偏心。为此，再次计算FIR滤波之后的正弦信号和余弦信号直流分量，分别为-0.009 4和0.002 3。事实上，读数头的四个通道上的光电器件的暗电流各不相同，通道的处理电路不完全对称，虽然经过差分放大器抵消，但还有一部分剩余量，导致直流电平偏离预定值。

我们滤掉其直流分量得到如图4所示，我们从图中可以看出两圆的圆心重合。我们知道，信号相位不正交和信号幅值不相等的李沙育图都会成椭圆形，从图4我们可以看出读数头输出的正余弦信号基本上是严格正交的，他们的幅值也基本上相等。利用波形数据统计求平均值的方法，计算得出相位偏差为周期的0.045 7%，幅度偏差即用正弦函数幅值相比余弦函数幅值得到1.013，这样质量的信号可以满足系统的1024细分［10］。

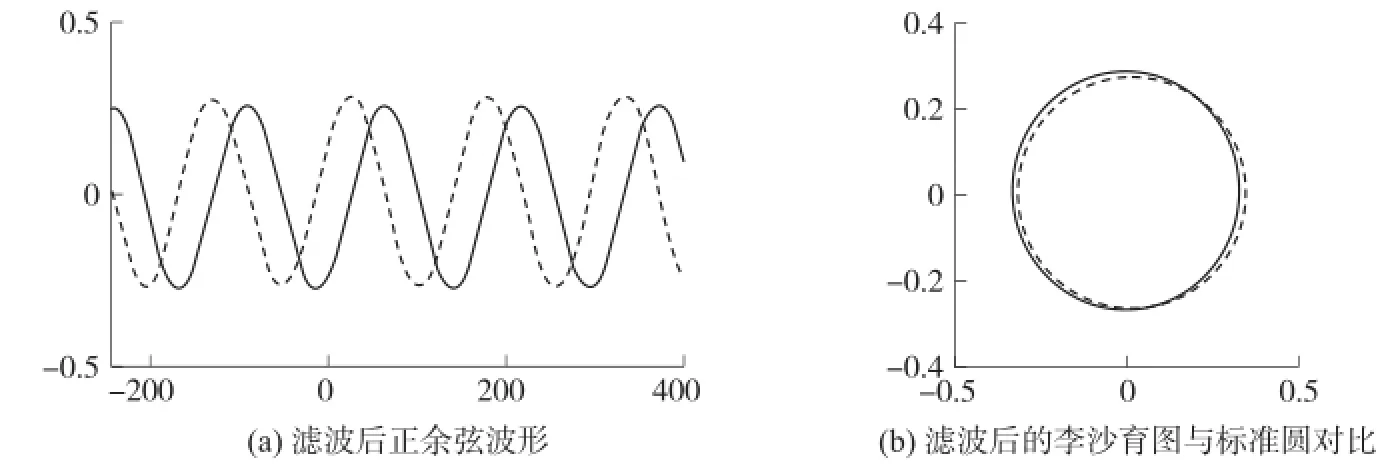
图3　滤波之后的对比图

图4　滤除直流分量后波形

2　细分算法及其误差分析

2.1细分算法

我们的细分算法采用前人提出的粗细分和精细分相结合的方法，但对前人的编码方式与数据处理方式作了一些修改，主要功能框图如图5所示。粗细分主要利用sin（ωt）、cos（ωt）、|sin（ωt）|、|cos（ωt）|这几个信号编码。sin（ωt）和cos（ωt）主要与过零比较器相比较，|sin（ωt）|与|cos（ωt）|相互比较。比较之后得到一个周期电平如表1所示。可以看出，一个周期变成8个不同的电平信号，分别为100、101、111、 110、010、011、001、000。当光栅正向移动的时候，信号电平按100-101-111-110-010-011-001-000-100的顺序循环变化。当光栅反向移动的时候，信号电平按110-111-101-100-000-001-011-010-110变化一次。这种信号电平的变化如图6（a）所示。当光栅每正向移动一次及八分之一栅距加计数，反向移动一次及八分之一栅距减计数，将数值记为count_8。如此就实现了8细分，即粗细分。

精细分主要将输入的正余弦信号离散化（取样）并用某种形式的线性函数进行近似，其主要包括2个步骤：AD采样和构造线性函数。构造线性函数方法主要有两种方法，第一种是将两路信号进行AD采样，再在MCU内部构造线性函数［11］。第二种方法主要利用模拟电路构造线性函数，也就是用模拟电路将正余弦信号转换成线性函数［12］。本文采用第二种方法，这样避免了复杂的算法运算，加快细分运算速度。构造的线性函数也有很多种，本文采用第二种方法，这样避免了复杂的算法运算，加快细分运算速度。构造的线性函数也有很多种，本文采用不太复杂的模拟电路构造正切函数和余切函数。如图6（b）所示。然后对这个线性函数进行AD采样，采样数据记为count_ad。精细分中线性函数的构造方法如下

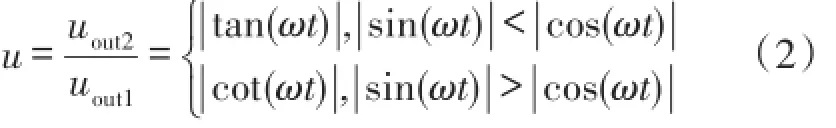
式中，uout表示正余弦信号绝对值较大的函数，uout2表示正余弦信号绝对值较小的函数。

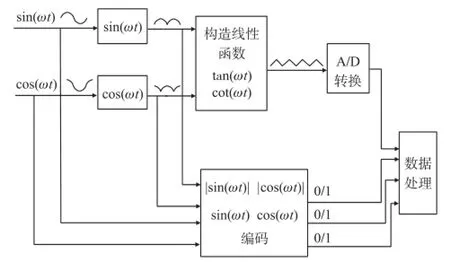
图5　细分算法功能框图

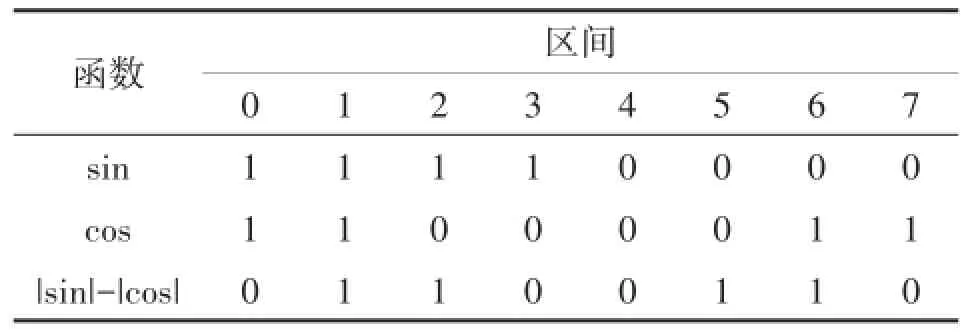
表1　信号极性与绝对值比较

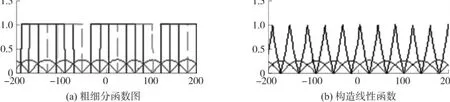
图6　细分算法构造函数

当光栅运动时，采用8 bit AD采样得到的时序关系如图7所示。这样采用8 bit AD，则总的细分数为8×28。根据前面实测正余弦信号的特点，取AD采样数据的高7位数据，则总的细分数为8×27。由图6（a）和图7可知，总的细分数据从上式可以看出，AD采样的误差不会累积。

图7　算法时序图

2.2线性函数构造的细分误差

构造线性函数导致的误差主要来源于函数的线性度导致的，如图8（a）所示。完全线性的函数其纵轴和横轴的刻度对应成正比例，纵轴的均分相当于横轴的均分。AD采样相当于对纵轴进行细分，实际构造的函数不是完全线性的，因此用AD采样的数据代替横轴均分的数据会带来误差。计算利用AD采样的数据代替横轴的时间轴细分的绝对误差最大为0.090 5。一个八分之一栅距计数为127，即绝对误差最大为127×0.090 5=11.493。由于钢带码盘刻了很多栅距，随着栅距数的增加，总的细分数据也将增加，最大的相对误差就会很小，可以忽略不计。

图8　线性函数对比及误差图

3　基于FPGA的高倍细分电路设计

为实现上节所述的细分算法，我们设计并制作了一个高倍细分系统，硬件框图如图9所示。该实验系统的输入信号是雷尼绍读数头SR050 A输出的四路相位各差90°的正弦信号，由于这些信号含有多种误差、噪声，需要首先对其进行处理；信号处理电路是差分放大与低通滤波，其输出为一路正弦信号和一路余弦信号。在此基础上，按照幅值采样的思想，将电路划分为两大主要部分：粗细分及辨向电路和精细分电路。但在具体的电路设计上，与文献［6］又有较大差别。具体来说，我们设计的粗细分及辨向电路由前端模拟电路和基于FPGA的后端逻辑电路构成，精细分电路则由前端模拟电路、8 bit ADC和基于FPGA的逻辑电路构成，只是构造线性函数的电路采用文献［6］介绍的电路。主要的特点是采用了FPGA进行细分逻辑电路的设计与实现，此外还增加了滤波电路。使用FPGA作为系统的数据处理模块，可以大大加快细分数据处理算法的运算速度，克服单片机或DSP导致的运算速度慢的缺点，从而提高了细分倍数。滤波电路的增加是基于前一节对实测读数头输出信号的分析而得出的，同时加耦合电容滤掉直流分量。

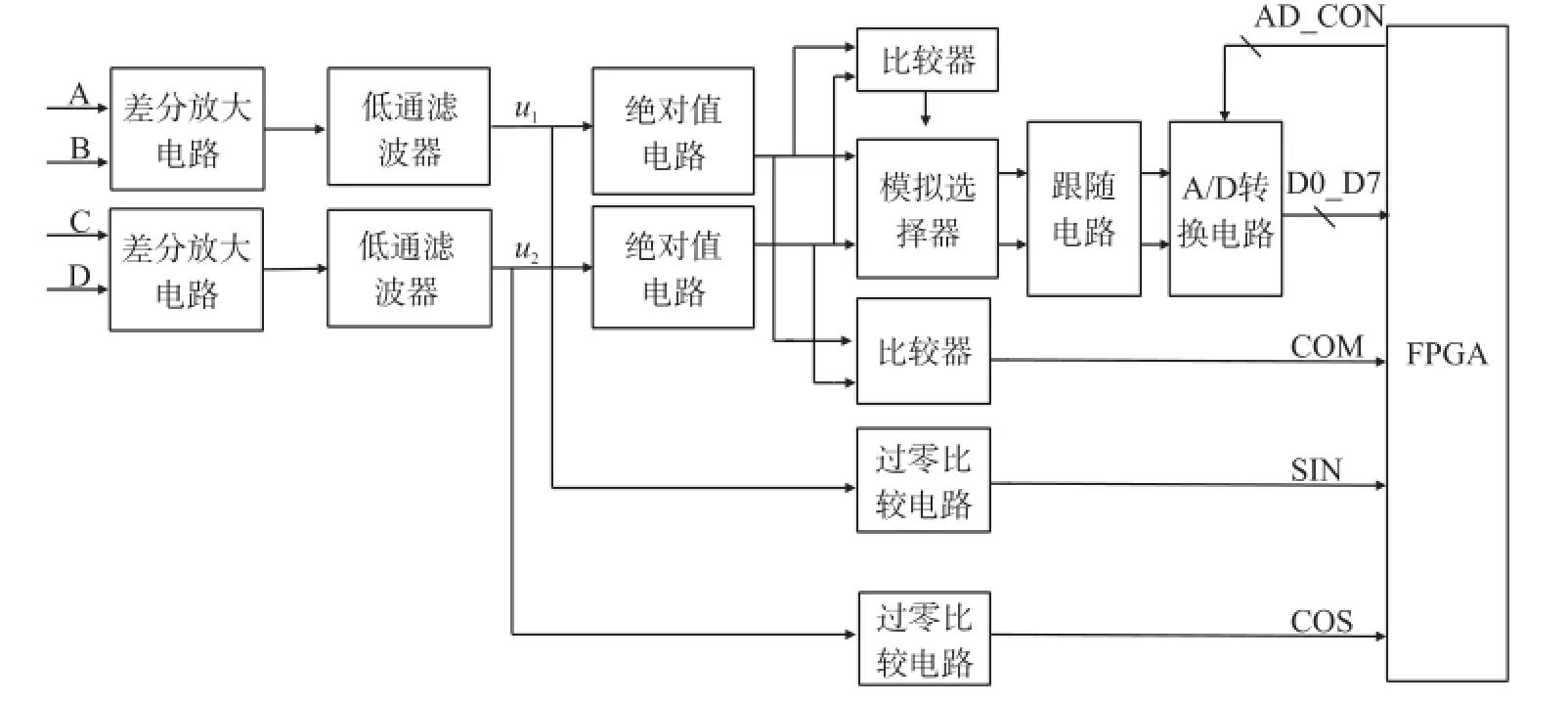
图9　系统硬件结构框图

3.1粗细分及辨向电路模块介绍

按光栅读数原理，光栅每移动一个栅距输出一个正弦波。粗细分就是要将这一个正弦波均分为8段，即八细分。也就是说，光栅每移动八分之一栅距，这部分电路完成一次计数。

粗细分模块电路主要由前端模拟电路和粗细分计数逻辑电路组成。粗细分前端模拟电路由图9中的一个绝对值比较器和两个过零比较器组成。两个结构相同的绝对值电路完成正余弦信号的绝对值运算，获得|sin（ωt）|和|cos（ωt）|，再由比较器对这两个绝对值信号进行比较，输出逻辑信号COM；两个结构相同的过零比较器对正余弦信号直接进行过零比较，输出逻辑信号SIN和COS。COM、 SIN、COS这三个信号的数值参见表1，它们作为FPGA内部粗细分计数逻辑电路的输入信号。

粗细分计数逻辑电路就是按照粗细分算法进行辨向（加或减）计数。当COM、COS、SIN这3路信号的电平按照100-000-001-101-111-011-010-110-100的顺序循环变化，进行加计数。COM、COS、SIN这3路信号的电平状态按照011-111-101-001-000-100-110-010-011的顺序循环变化，进行减计数。仿真如图10所示，同时我们用Quar⁃tus II内置逻辑分析仪Signal Tap II捕捉粗细分信号的数据如图11所示，其中的signal信号即COM、COS、SIN，数据在时序上严格根据信号的变化计数。

图10　仿真实验图

图11　逻辑分析仪数据

3.2精细分模块电路设计

精细分模块电路设计主要是将每个周期的信号构造成8个线性区间，然后逐次采样得到每1/8区间信号的数据。精细分电路包括图9中的两个绝对值电路及其比较、多路选择电路、跟随电路以及AD采样电路。两路正余弦电路经过绝对值电路后，再经过多路选择器及跟随器的信号uout1和uout2输至AD芯片端，uout1为较小的信号，如图12绿色所示，uout2为较大的信号，如图12黄色曲线所示。将信号uout1送入A/D芯片的模拟输入端ANALOG_IN，信号uout2送入A/D芯片的参考输入端REFT。这样A/D芯片的参考电压是变化的模拟信号，对于这种变化的参考信号，A/D采样输出精细分数据。

以上处理实质上是用一块A/D芯片TLC5510，巧妙地完成了对正、余弦信号的正切函数转换和A/D幅值采样，避免了复杂且耗时的除法电路［6］，完成精细分。A/D转换电路最终输出的是对信号采样后的数字信号，以供FPGA处理。

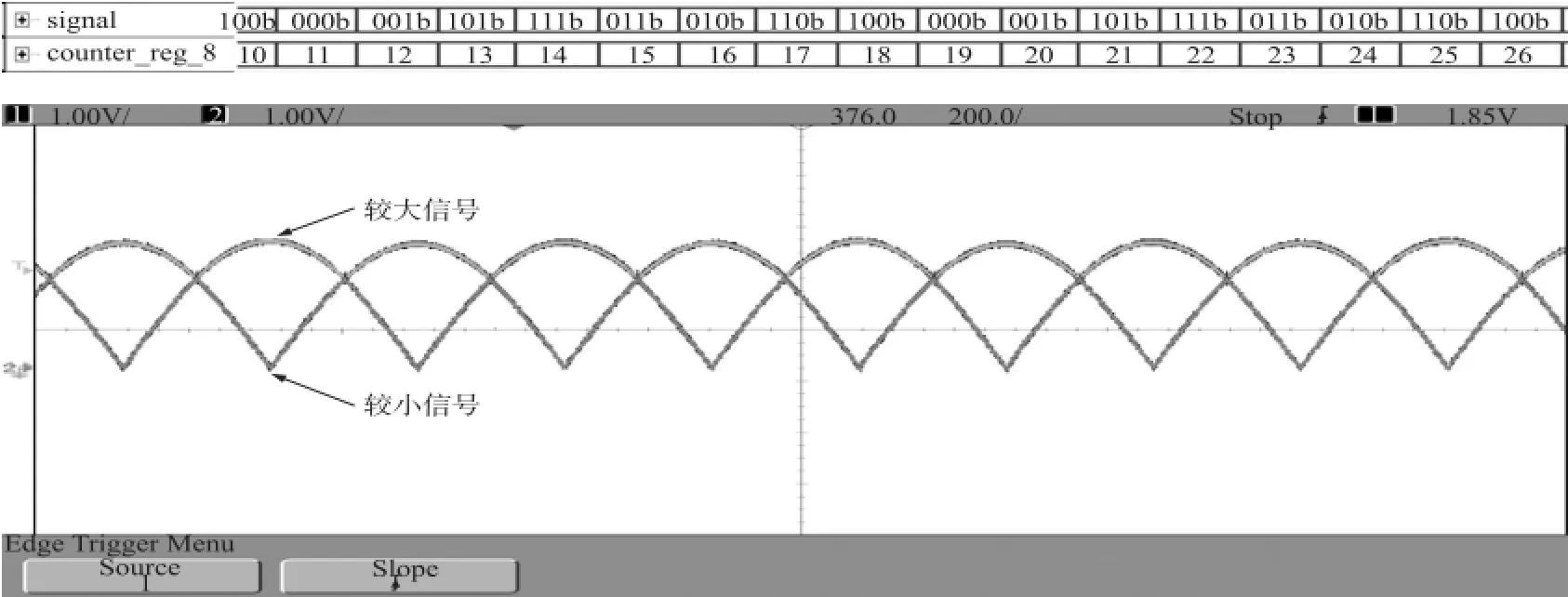
图12　输入至AD芯片模拟输入端波形

3.3FPGA数据处理模块

根据前述细分原理和系统结构图可知，FPGA主要完成ADC控制、数据接口、粗细分和精细分的综合，我们设计了对应的子模块完成相应任务，主要包括A/D控制模块、数据缓冲模块及8细分模块和综合数据处理与输出模块，这些子模块的数据输入输出和互连关系如图13所示。

图13　FPGA内部逻辑电路设计

A/D控制模块主要是连接控制A/D转换芯片TLC5510的时钟输入端。数据缓冲模块主要是为了接受精细分输出数据data_out，8细分模块得到粗细分数据counter_reg_8。综合数据处理模块主要对得到的粗细分数据和精细分数据进行运算得到高倍细分的数据data，计算公式参见式（4）。举例来说，若采用码盘的线数为c，每个周期正弦信号的细分倍数为1 024，则转动角度的计算公式为

4　实验结果及其分析

Altera公司提供了一种加快开发速度的板级调试工具SignalTap II逻辑分析仪。本文主要用Sig⁃nalTap II进行实时采集信号观察。SignalTap II是Quartus II软件中内置的逻辑分析仪软件，使用它可以实时地观察FPGA内部信号波形，方便设计者来查看设计缺陷，相当于一种在线调试工具。

逻辑分析仪的信号端口主要观察三个端口da⁃ta_out、counter_reg_8和sum。data_out为精细分数据，counter_reg_8为粗细分数据，sum为总的细分数据。图14为精细分数据处于最大值的临界状态时，当粗细分数据位于偶数区间，及图中的coun⁃ter_reg_8等于6时可以看出公式（3）提出的偶数计算公式是正确的。当粗细分数据位于奇数区间，及图中counter_reg_8等于7时可以看出上节提出的奇数计算公式是正确的。

图14　逻辑分析仪捕捉最大值临界状态

同理从图15中，可得精细分数据在最小值的临界状态也是正确的。图11已说明8细分数据是正确的，图14和图15再次得到和图7理论分析一样的时序图证明1 024细分是正确的。

图15　逻辑分析仪捕捉最小值临界状态

为了得到整体数据的变化规律，将每一个栅距作为一次循环，及计数到1 023时数据，从头开始。将数据转化成模拟量，可以看到数据的变化规律如图16所示。

图16　数据变化规律

本文实验所采用的数据来源于用安捷伦6000系列示波器采集的雷尼绍读数头SR050 A输出的信号。通过可编程函数信号发生器再将这些实测数据转化成后续实验分析和测试的波形。这为分析、设计和调试高倍细分电路带来了很大的便利。实验过程中使用的都是实际波形数据。对于1 024细分电路的实测结果是可信的。由于采用对光栅信号的预处理后，正余弦信号波形满足高倍细分电路的要求。

搭建的细分电路主由8细分和精细分相结合的方法，可靠性和处理速度得到了提高。粗细分改变电路采用移相电阻链的细分方法，由于电阻不是严格精密电阻，会引入较大误差。因此采用本文的粗细分模块提高了细分精度。精细分中由于构成的线性函数是正切和余切函数，函数并不是严格线性的，会造成一定的线性误差，导致采样的数据位时间不是严格相等，因此，这种方法在目前情况下，只能做到1 024细分。

5　结论

本文通过Matlab分析读数头输出的两路原始信号的特点，对其进行滤波和滤除直流分量，根据处理之后的波形构造细分算法并分析其构造的线性函数误差。首先通过Matlab验证了细分算法实现1 024细分的可行性，也验证硬件电路实现算法的可行性，同时我们通过理论分析得到细分算法的时序图。采用粗细

分和精细分相结合的细分方法，根据Matlab构造的细分算法框图，搭建细分硬件电路。硬件环境下，首先我们通过逻辑分析仪捕捉8细分计数信号，证明8细分是正确的，然后通过SignalTap II捕捉信号时序图，最后得到和我们理论分析一样的时序图，证明本文实现1 024倍细分的正确性。全硬件细分电路使光栅细分速度得到提高，细分倍数主要取决于光栅信号质量，在光栅信号质量很好的情况下，构造线性度更好的函数，调整A/D位数就可以得到更高倍细分。

［1］刘浩，冯济琴，陈自然.基于预测理论的光栅信号精密细分方法研究［J］.传感技术学报，2015，28（4）：469-473.

［2］楚兴春，吕海宝，赵尚弘.大量程纳米级光栅干涉仪位移测量［J］.光电工程，2008，35（1）：55-59.

［3］王显军.光电轴角编码器细分信号误差及精度分析［J］.光学精密工程，2012，2（1）：213-219.

［4］Luis Miguel，Sanchez-Brea，Tomas Morlanes.Metrological Errors in Optical Encoders［J］.Measurement Science And Technology，2008，11（19）：1-9.

［5］熊文卓，孔智勇，张炜.光电轴角编码器光电信号正交性偏差的相量校正方法［J］.光学精密工程，2007，11（15）1746-1748.

［6］刘世峰.基于幅值采样的光栅莫尔条纹信号细分技术的研究［D］.武汉：华中科技大学，2007：41-75.

［7］喻洪麟，黄良明，王远干.莫尔条纹信号的DSP滤波及细分技术研究［J］.光电工程，2004，31（9）：61-65.

［8］曹永刚，赵立荣.光电编码器硬件细分方法［J］.仪器仪表学报，2011，6（32）：372-374.

［9］胡泊，李彬华.低温下EMCCD电子倍增模型［J］.电子学报，2013，9（9）：1826-1830.

［10］马泽龙.正余弦编码信号纠偏与细分技术研究［D］.武汉：华中科技大学，2012：1-57.

［11］罗华，高山，李翔龙.粗光栅信号全数字化处理法实现高倍数细分［J］.光学精密工程，2007，2（15）：283-288.

［12］Design of a Precise and Robust Linearized Converter for Optical Encoders Using a Ratiometric Technique［J］.Measurement Sci⁃ence and Technology，2014，9（25）：1-9.

丁旭（1990-）男，安徽舒城人，硕士研究生，主要研究方向为精密测量，dx409@ qq.com；

李彬华（1963-）男，江西南昌人，博士，教授，硕士生导师，本文通信作者，主要研究方向为电路与系统理论、探测与成像技术、天文技术方法，lbh@bao.ac.cn。

EEACC：723010.3969/j.issn.1004-1699.2016.06.010

一种基于FPGA的光栅信号细分方法*

丁旭，李彬华*，杨晓晗
（昆明理工大学信息工程与自动化学院，昆明650500）

在高精度测量中，为了提高光栅细分精度，采用了一种基于FPGA的光栅信号细分及辨向方法。首先用Matlab分析读数头输出的两路原始信号和经过滤波且滤除直流分量的信号特点，并根据处理后的波形构造细分算法，既验证细分算法实现1024细分的可行性，也验证硬件电路实现细分算法的可行性。然后在Matlab对光栅信号的算法分析基础上，设计了一种基于幅值采样细分方法的电路，实现对光栅信号进行细分和辨向。细分硬件电路主要包括8细分电路和精细分电路，8细分电路主要对每个信号的一个周期进行8细分，精细分电路主要是对每1/8周期的信号进行细分。测试结果表明，该细分电路实现了光栅的1024细分，达到了高倍细分目的。

FPGA；光栅信号；测量；细分；辨向

TP391

A

1004-1699（2016）06-0846-08

2015-11-29修改日期：2016-02-14

项目来源：国家自然科学基金天文联合项目（10978103）