基于信息不对称和预售的采购合同研究
杨 勇
(天津大学 管理与经济学部,天津 300072)
基于信息不对称和预售的采购合同研究
杨勇
(天津大学 管理与经济学部,天津 300072)
以一个由零售商和供应商组成的二级供应链系统为研究对象,考虑到零售商在销售季开始前预售产品,供应商按MTO模式进行生产。构建以零售商为主者、供应商为从者的“委托-代理”模型,研究在供应商生产成本为不对称信息的情况下零售商最优采购合同设计问题,并与完全信息条件下的最优采购合同进行比较。结果表明,信息不对称不仅降低了零售商的收益,同时也降低了供应链整体的收益,但供应商可以从中获利。
合同理论;信息不对称;预售策略;备货时间;委托代理模型
在当前以客户为中心的市场竞争环境中,响应客户需求的时间长短(即响应速度)已经成为新的竞争维度[1]。 在供应链中,上游供应商能否准时供货,直接决定零售商能否准时将产品销售至终端市场,并最终影响零售商的利润。在此过程中,零售商作为主导者,会采取一定的措施激励上游供应商准时供货。在按订单生产的供应链中,供应商在接到零售商订单后才能组织生产,其生产能力是影响最终交货时间的重要因素。一般而言,有优势的供应商拥有更好的基础设施和规模经济效应。但在短期内,其科技水平和社会状况不会发生根本性变化,供应商可支配资源有限。为了在约定时间内完成订单,供应商必然要付出一定努力,包括加大投入成本。由于供应链中存在信息不对称现象,零售商无法观测到供应商的努力程度。因此,零售商需要设计最优激励机制,避免逆向选择问题,促使供应商能够准确汇报自身的真实类型并付出相应的努力,进而实现自身利润最大化。对于下游消费者来说,零售商也会采取一定的策略来吸引消费者,例如预售策略(advance selling,AS),即在产品还未完全上市之前抢占部分消费者市场,并在一定时间内将产品交付给消费者。因此,研究零售商如何激励供应商与零售商的预售策略具有重要意义。
杨文胜等[2]针对准时采购中采购商与供应商之间的动态交互行为,建立以采购商为主方的主从博弈模型。LIU等[3]研究了在供应商和零售商组成的二级供应链中,市场需求受价格和交货时间影响的情况,构建了以供应商为主方的Stackelberg博弈模型,并分析了价格与交货时间的决策问题。但上述文献没有考虑不对称信息的影响。
预售策略是一种协调生产和销售的重要手段。对于零售商来说,预售可以提前获得销售资金,有助于进行需求预测,以降低库存风险。对于消费者来说,提前购买产品除可以享受到一定的价格折扣外,也可以避免销售季的缺货风险[4]。TANG等[5]分析了预售对零售商收益的影响,得出零售商通过折扣预售一种易逝品来匹配供给与需求以减少缺货风险和库存风险的结论。BOYACI等[6]研究了制造商为了从零售商处获得准确的市场需求信息,来制定产能计划以及何时开始与何时结束面向零售商的预售计划。但上述文献没有考虑供应商供货时间对供应链及预售的影响。
研究供应商和零售商之间的最优合同设计问题的文献主要利用了信息经济学中的“委托-代理”理论。在“委托-代理”的文献中,KOSTAMIS等[7]研究了在市场需求信息和代理人成本双重信息不对称情况下,委托人采购合同设计问题。AKAN等[8]研究了信息不对称和规模经济效益下服务合同的设计问题。上述文献并没有考虑供应商的供货时间问题和零售商的预售问题。虽然有大量文献分别研究预售和供货时间,但将两者同时考虑的文献较少。WU等[9]以零售商为主者,预售一种半成品,并根据客户要求进行定制,且在定制完成后交付给消费者,其未考虑半成品采购过程中的等待时间。笔者旨在运用“委托-代理”理论,以零售商为委托人,供应商为代理人,分析预售策略下的最优采购合同设计。
1 问题描述和基本假设

零售商会采取预售和正常销售两种策略销售该产品。如果消费者选择在预售阶段购买该产品,需要支付价格rp且需要等待t时间后才能拿到产品;如果消费者选择在正式销售阶段购买该产品,则需要支付价格p,并且可以立即拿到产品。笔者假设零售商是市场价格的接受者,即预售价格rp和销售价格p为外生变量,且rp (1) 同理,正式销售时购买该产品顾客的比例为: (2) 假设提前销售期间,顾客到达率为M,正式销售期间,顾客到达率为N,销售期的总时长为T,市场总需求D可表示为: (3) 从式(3)可看出,市场需求受供货时间的影响,零售商为了提高产品销量来提高总收益,需要制定最优的供货时间。双方的决策顺序如图1所示。 图1 双方决策顺序 (1)零售商在不知道供应商努力程度的情况下给其提供一个菜单合同{w(·),t(·)},供应商根据自身的类型决定是否接受该合同,如果拒绝合同,供应商只能获得保留收益; (2)如果供应商接受并选择合同{w(c),t(c)},同时,零售商开始以价格rp预售该产品,并告知消费者等待时间t(c); (3)销售季开始,零售商陆续给预定的顾客发货,并开始以价格p销售该产品; (4)销售季结束,供应商、零售商和消费者获得各自的收益。 笔者旨在帮助零售商设计一个最优的采购合同,激励供应商真实地报告生产成本,并确定最终交货时间,使得零售商获得最大的收益,从而避免逆向选择问题。 2.1目标函数 付出成本为c的供应商从零售商提供的合同中选择{w(c),t(c)}的菜单合同,其总收益可表示为: (4) 其中,π(c,c)表示供应商真实的生产成本为c、向零售商汇报的成本为c时的收益。 零售商通过为供应商设计合同来使自身的期望收益最大化,零售商的目标函数为: (5) 2.2约束条件 2.2.1激励相容约束(IC) 激励相容约束保证供应商能够真实地汇报自身类型,并选择相应的合同收益不低于谎报该类型所获的收益。即: (6) 具体可以写成: (7) 2.2.2参与约束(IR) 零售商在自身收益最大化的同时,也要保证供应商能够获得最低收益,以促使供应商参与交易。参与约束保证供应商接受合同所获的收益不低于拒绝合同的收益。为了不失一般性,笔者假设供应商外部选择的收益为0,即使供应商最终的收益等于拒绝合同时的收益,其仍然会接受合同,并给零售商提供同质量的产品。故参与约束可以表示为: (8) 具体可以表示为: (9) 2.3最优采购合同 综上所述,零售商的最优化问题可以表示为: (10) 在对称信息下,零售商和供应商双方在签订合同之前都能观察到供应商的私人信息,因此,在处理问题时可直接忽略激励相容约束,只需要考虑参与约束,即只需要保证供应商获得的收益不低于其保留收益。在最优的情况下,参与约束是紧约束,即零售商支付给供应商的批发价格等于供应商的生产成本,此时,零售商的优化问题可表示为: (11) 定理1对称信息条件下,最优供货时间为: (12) 证明将式(1)~式(3)代入式(11)后所得的目标函数是关于t(c)开口向下的二次函数,即存在最大值,对该式求一阶导数得: (13) 令式(13)等于零,即可求得对称信息下最优的备货时间ts(c)。可看出ts(c)是关于c的减函数,即供应商的供货时间会随着供应商的生产成本增加而降低。 定理2完全信息条件下,零售商支付的批发价格为: (14) 证明完全信息条件下,供应商的生产成本为公共信息,零售商支付的批发价格只要不低于供应商的生产成本,就能确保供应商参与交易。同时,零售商最终目标是使自身收益最大化。因此,零售商最终支付的批发价格即为供应商的生产成本。对于供应商来说,不管付出多少成本,其获得的收益都为零,即: πs(c)=(w(c)-c)D=(c-c)D=0 (15)此时,零售商可以获得供应链的全部收益: (16) 结论1在信息对称条件下,零售商可以通过设计合同获得供应链的全部收益,而供应商的最终收益为零。 由于存在信息不对称,零售商不能准确获取供应商的私人信息,只知道供应商付出成本的分布情况。从而零售商需要向供应商提供一个菜单合同{w(·),t(·)}供其选择,供应商选择{w(c),t(c)},零售商的优化问题就可表示为: (18) 对于其他类型的供应商来说,其目标是要极大化自己的收益。零售商需要解决的问题就是: (19) 式中:c为供应商的实际生产成本;c′为供应商报告给零售商的生产成本。对式(19)积分可推出零售商的实际收益,即: (20) 结合式(4),可知: (21) 将式(21)代入式(17),零售商的利润可表示为: (22) 对式(22)进行分部积分可得: (23) 式(23)关于t(c)的二阶变分为: (24) 其中: (25) 定理3非对称信息情况下,最优的供货时间为: (26) 证明由式(23)的一阶条件即可解出最优的备货时间ta(c)。由于F(c)/f(c)是关于c的单调增函数,因此ta(c)是关于c的单调减函数,即ta(c)会随着供应商努力程度的增加而降低。 定理4非对称信息情况下,零售商支付的批发价格为: (27) 其中: 证明将式(26)代入式(21),并进行变形即可得到式(27)。 结论2信息不对称条件下,供应商的供货时间要小于在完全信息情况下的供货时间。 证明由式(12)和式(26)相减可得: (28) 结论3信息不对称条件下,市场需求要比完全信息条件下市场需求低,零售商有促使供应商共享信息的动机。 证明式(3)可改写为: (29) 可看出市场需求D(c)是t(c)的二次函数,在to(c)处取到最大值,由式(12)、式(26)以及结论2可知ta(c) (30) 结论4信息不对称条件下,供应商获得的批发价格要高于完全信息情况下供应商获得的批发价格,供应商有隐藏信息的动机。 证明由式(27)和式(14)相减可得: (31) 结论5信息不对称条件下,供应商的收益要高于完全信息下供应商的收益,供应商有隐藏信息的动机。 证明完全信息条件下,供应商获得的批发价格ws=c,供应商的收益为0。在信息不对称条件下,由引理1可知wa>ws,因此有πa>πs,其中πa-πs为零售商付给供应商的信息租金。 供应商在不对称条件下可获得一定的信息租金,信息租金的值为供应商在信息不对称条件下和信息对称条件下的收益之差。 结论6信息不对称条件下,零售商的收益要低于完全信息条件下零售商的收益,零售商有促使供应商分享信息的动机。 证明由上述分析可知,由于信息不对称的存在,供应链整体收益会下降。在完全信息条件下,零售商支付给供应商的转移支付为0,零售商的收益等于供应链的整体收益;而在信息不对称的情况下,零售商需要支付给供应商一定的信息租金,从而进一步降低了零售商的收益。可以看出,信息不对称的情况下,零售商的收益要低于完全信息情况下的收益。 结论7信息不对称条件下,供应链的整体收益会下降。 证明供应链的总收益可表示为: (32) 可看出ψ(c)是关于t(c)的二次函数,在te(c)处取到最大值,由式(12)、式(26)以及结论2可知ta(c) (33) 考虑到市场需求随供应商供货时间变化,零售商采取预售策略的情况下,笔者研究了零售商关于供应商的最优合同设计问题,应用“委托-代理”理论,分别给出在完全信息和信息不对称条件下,批发价格和供货时间的最优合同设计并进行了对比。研究表明,当供应链中存在隐藏信息时,隐藏信息会导致供应商的供应时间和市场需求的扭曲,供应商的供应时间会向下偏移,供货时间缩短进而导致需求的下降。此外,由于供应商供货时间随供应商成本增加而缩短,供应商会在选取供货时间时故意选取较短的供应时间来获取较高的收益。同时由于私人信息的存在,会使供应链的整体效益下降,零售商的收益也会下降。 [1]王福寿,马士华,杜旌.价格对时间敏感时的供应链响应时间决策研究[J].物流技术,2005(7):64-67. [2]杨文胜,李莉.基于Stackelberg模型的准时交货激励契约分析[J].系统工程理论与实践,2006,3(12):17-23. [3]LIU L, PARLAR M, ZHU S X.Pricing and lead time decisions in decentralized supply chains[J].Management Science, 2007,53(5):713-725. [4]李勇建,许磊,杨晓丽.产品预售、退货策略和消费者无缺陷退货行为[J].南开管理评论,2012(5):105-113. [5]TANG C S, RAJARAM K, ALPTEKINOGLU A, et al.The benefits of advance booking discount programs: model and analysis[J].Management Science, 2004,50(4):465-478. [6]BOYACI T, ÖZER Ö.Information acquisition for capacity planning via pricing and advance selling: when to stop and act[J].Operations Research, 2010,58(5):1328-1349. [7]KOSTAMIS D, DUENYAS I.Purchasing under asymmetric demand and cost information: when is more private information better[J].Operations Research, 2011,59(4):914-928. [8]AKAN M, ATA B, LARIVIERE M A.Asymmetric information and economies of scale in service contracting[J].Manufacturing & Service Operations Management, 2011,13(1):58-72. [9]WU Z, KAZAZ B, WEBSTER S, et al.Ordering, pricing and lead-time quotation under lead-time and demand uncertainty[J].Production and Operations Management, 2012,21(3):576-589. [10]MENDELSON H, WHANG S.Optimal incentive-compatible priority pricing for the M/M/1 queue[J].Operations research, 1990,38(5):870-883. Procuring under Asymmetric Information and Advance Selling YANG Yong In the customer-centric market environment full of competition, demands are sensitive not only to the price but also the time.A two-tier supply chain consisting of a retailer and a supplier is studied.Supposing the retailer presells products ahead of selling season and the supplier produces under MTO mode.A principal-agent model in which the retailer acts as the game leader and the supplier acts as the game follower is set in order to investigate the optimal procurement contract under the asymmetric information about the producing cost of the supplier and compare it with the contract under symmetric information.The conclusion shows that the asymmetric information hurts both the retailer and the supply chain, but benefits the supplier. contract theory; asymmetric information; advance selling; lead time; principal-agent model YANG Yong:Postgraduate; College of Management and Economics, Tianjin University, Tianjin 300072, China. 2095-3852(2016)04-0474-06 A 2016-02-29. 杨勇(1992-),男,江苏盐城人,天津大学管理与经济学部硕士研究生. 国家自然科学基金项目(71471126). F272.3 10.3963/j.issn.2095-3852.2016.04.017
2 模型建立




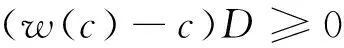
3 对称信息下的预售合同设计
4 非对称信息下的合同设计

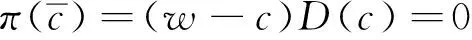

5 结论

