硅烯量子点二聚物的等离激元激发

尹海峰

（1凯里学院物理与电子工程学院，贵州凯里556011；2武汉大学物理科学与技术学院，武汉430072）

硅烯量子点二聚物的等离激元激发

尹海峰1，2，*

（1凯里学院物理与电子工程学院，贵州凯里556011；2武汉大学物理科学与技术学院，武汉430072）

基于含时密度泛函理论，研究了随着间距改变时硅烯量子点二聚物的等离激元激发特性。沿垂直于硅烯所在平面方向激发时，在一定间距范围内，硅烯量子点二聚物中形成了长程电荷转移激发模式。参与长程电荷转移激发的π电子主要在两个量子点之间运动。该等离激元模式随着间隙的减小发生蓝移。此外，在不同间距时，体系中还有两个等离激元共振带，分别位于7和15 eV附近。沿平行于硅烯所在平面方向激发时，由于两个量子点之间的耦合，在低能光谱区，硅烯量子点二聚物吸收光谱的线形以及相应吸收峰的强度都和单个硅烯量子点吸收光谱的一样。

等离激元；硅烯；二聚物；含时密度泛函理论

1　引言

石墨烯是由碳原子构成的蜂窝状结构的单原子层二维材料。在低能区，其色散关系是线性的，由于其特殊的能带结构，石墨烯具有众多的新颖物理现象和应用潜能1，2。在石墨烯成功制备之后，科学家开始探索制备其它的二维材料。最近，单原子层薄膜硅烯已经成功合成3－9。由于硅与碳在元素周期表中均为四主族元素，因此人们预言硅烯的电子性能和石墨烯的相似。此外，相对于石墨烯，硅烯有以下两个优点。首先，硅烯更容易与硅为基础的现代电子工业结合起来。其次，硅烯的稳定结构为低翘曲度结构，形成了sp2和sp3杂化轨道混合的情况。低翘曲度结构会使硅烯中的自旋轨道耦合增强，这可以带来许多有趣的物理现象，比如量子霍尔效应4，5。

等离激元是微纳材料表面的自由电子同入射光子相互耦合形成的非辐射电磁模式，是一种混合激发态10。由于等离激元具有选择性光吸收和散射以及局域电场增强等特点，可以应用于共振传感器、表面增强光谱等方面11－13。对于硅烯，Mohan等14研究发现沿硅烯所在平面方向，在能量共振点2.1和7.6 eV附近，体系中分别存在π和π+σ等离激元激发；而沿垂直于硅烯所在的平面方向，在较低的能量区域，不存在等离激元激发。近来的研究发现硅烯的等离激元激发特性，还取决于温度、外加的电场以及磁场15－17。对于硅烯纳米结构，由于尺寸和量子受限效应，沿纳米结构所在的平面方向，体系中两个等离激元共振带发生了展宽和劈裂；随着硅烯纳米结构尺寸的增加，体系的两个等离激元共振带都会发生红移18。近年来，纳米颗粒聚集体的等离激元研究也一直受到关注，特别是对于纳米颗粒二聚物的研究尤其受到重视。这主要是由于对二聚物的研究有助于理解不同纳米结构之间等离激元的杂化机理。作为一般的特征，随着间隙的改变，金属纳米颗粒二聚物间存在三种截然不同的相互作用区19，20。由于纳米颗粒的等离激元特性依赖于纳米颗粒的形状和材料，人们开始研究了不同形状和材料的纳米颗粒二聚物的表面等离激元特征21。在本文中，我们将系统地研究硅烯量子点二聚物的等离激元激发特性，采用含时密度泛函理论，主要探究随着间隙改变时，硅烯量子点二聚物的等离激元激发的演变规律。

2　计算方法

采用含时密度泛函理论计算硅烯量子点二聚物的吸收光谱。所有的计算都是用实时、实空间的OCTOPUS软件22来完成的。在量子点边界处，硅的悬挂键用氢原子进行了饱和。采用模守恒赝势23描述原子，对基态和激发态的计算，交换关联势使用的都是局域密度近似24。硅烯量子点二聚物位于实空间模拟所用盒子的中心，原子到模拟盒子边界的最近距离为1 nm。在模拟盒子内使用间距为0.032 nm的均匀格点。基于含时密度泛函理论可以采用两种方式计算光吸收谱。一种方式是在外场激发下，含时演化波函数方法；另外一种方式是在频率空间求解Casida方程。本文采用第一种方法18，时间的演化步长为3.3×10－18s，电子波函数的演化总时间为2.6×10－14s。

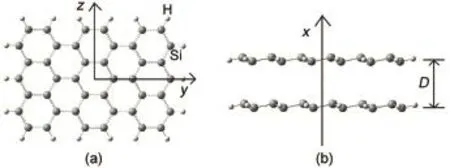
图1　硅烯量子点二聚物的结构示意图Fig.1　Schematic diagrams of silicene quantum dot dimer For Fig.1　（a），the silicene quantum dot plane is parallel to the y-z plane. Fig.1　（b）shows the side view of silicene quantum dot dimer. The x-axis is perpendicular to the silicene quantum dot plane. D represents the spacing between the two silicene quantum dot.

3　结果与讨论

图1是硅烯量子点二聚物的结构示意图。我们主要考虑的是矩形硅烯量子点。图中深色球和浅色球分别表示硅原子和氢原子。采用笛卡尔直角坐标系，坐标系原点位于立方体模拟盒子的中心，硅烯量子点所在的平面平行于y-z平面。选取的硅烯量子点，都是基于第一性原理优化后的稳定结构18。主要讨论随着二聚物之间的间距D改变时，硅烯量子点二聚物等离激元激发的演变特性。

图2给出了沿垂直于硅烯所在平面方向激发，随着二聚物之间的间距D改变时，硅烯量子点二聚物的吸收光谱。其中，图2（a）是沿垂直于硅烯所在平面方向激发时，单个矩形硅烯量子点的吸收光谱。硅烯量子点中有两个主要的等离激元共振带。与沿单个硅烯量子点所在平面方向激发时所不同的是18，这两个等离激元共振带都位于能量较高的光谱区。其中，位于7 eV附近的等离激元共振带较窄、吸收强度较弱，而位于15 eV附近的等离激元共振带较宽、吸收强度较大。当二聚物之间的间距D较大、即间隙处的势垒较大时，两个硅烯量子点间的相互作用是电容性的。两个硅烯量子点靠近时，7 eV附近的等离激元共振带随着间距的减小发生了红移。这主要是由于该等离激元激发模式中有部分离域化的π电子参与。离域化的π电子和金属中的自由电子特性相近，对于金属纳米二聚物，在经典相互作用区，随着间距的减小，二聚物的等离激元共振带也发生红移19。比较有意思的是，随着间距D的进一步减小时，在近红外光谱区0.6 eV附近，长程电荷转移激发模式逐渐形成。随着间距的减小，该激发模式逐渐蓝移。这种演化规律与金属纳米二聚物长程电荷转移激发模式的演化规律相同19。不过与金属纳米二聚物不同的是，随着间距D再进一步减小时，由于二聚物中两个量子点之间的耦合加强，长程电荷转移激发模式逐渐消失。此外，随着二聚物之间的间距D由0.7 nm减小到0.3 nm时，高能共振区15 eV附近的等离激元共振带几乎不发生移动。这主要是由于参与该能量区域共振激发的是形成sp3轨道的σ电子。σ电子的离域性较弱，其聚集激发时电子主要在原子实附近振动。因此，随着间隙改变，尽管二聚物间相互作用的形式发生改变时，其共振带也几乎不发生移动。

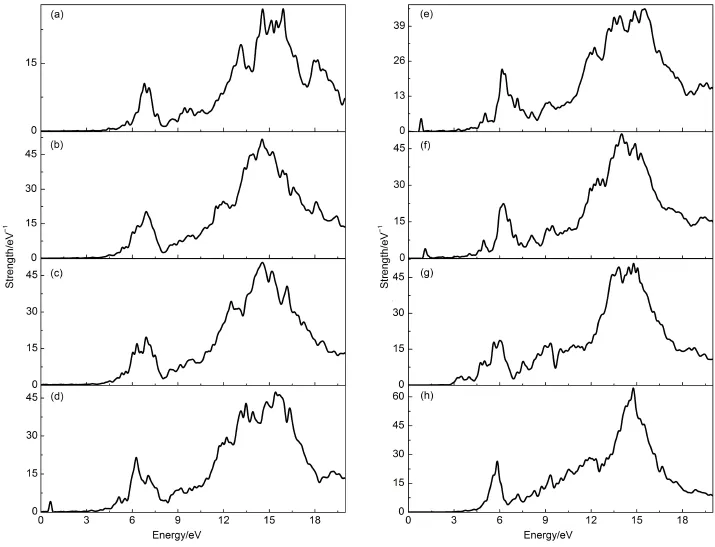
图2　沿x轴方向激发时，随着二聚物之间的间距（D）改变硅烯量子点二聚物的吸收光谱Fig.2Optical absorption spectra of silicene quantum dot dimers，with variable number of the gap distance（D），to an impulse excitation polarized along x-axis direction（a）the optical absorption of single silicene quantum dot.（b－h）Corresponding gap distances are 0.3，0.35，0.45，0.5，0.55，0.65，and 0.7 nm.

为了进一步说明硅烯量子点二聚物等离激元共振的物理机制，我们计算了依赖于共振频率的电流和不同共振频率所对应的诱导电荷密度分布。通过硅烯量子点二聚物间隙中间处的电流公式为I（t）=∫Sj（r，t）∙dS。其中，S为间隙处电流通过的一个面，该面垂直于x轴，与硅烯量子点所在平面平行。电流密度为：

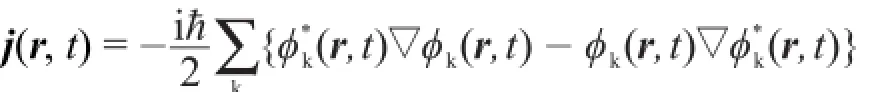
图4分别给出了沿如图1所示的x轴激发，间距为0.5 nm时，在等离激元能量共振点0.84、6.15和14.86 eV处的傅里叶变换诱导电荷密度分布，以及间距为0.3 nm时，在能量共振点5.84和14.77 eV处的傅里叶变换诱导电荷密度分布。傅里叶变换诱导电荷密度计算公式为其中，T为电子波函数的演化总时间，ω为振动频率。图4给出的诱导电荷密度平面是经过坐标原点的x-y平面，图中箭头所指的方向为硅烯量子点中原子实所在的位置。图4（a）所示的是近红外光谱区0.84 eV处长程电荷转移激发的诱导电荷密度。图4（a）表明，参与该模式等离激元共振的π电子主要集中在两个量子点中间处运动。因此，当间距D较小时，两个硅烯量子点之间的强耦合促使该等离激元共振模式消失。由于σ电子和π电子共同参与了6.15 eV的等离激元共振，图4（b）的结果表明，沿着激发方向，一个硅烯量子点附近主要是负的诱导电荷；在量子点中原子实所在的位置，由于σ电子的参与以及原子势的局域束缚，呈现正的诱导电荷；而另一个硅烯量子点附近主要是正的诱导电荷，在量子点中原子实所在的位置呈现负的诱导电荷；在量子点之间诱导电荷密度呈现振荡行为。对于14.86 eV能量较高的等离激元共振，图4（c）的结果表明，其诱导电荷密度类似于两个偶极子，参与该模式共振的大部分是σ电子，σ电子在硅原子实附近运动。当间距D为0.3 nm时，通过对比图4（d）与（b），以及图4（e）与（c），结果表明由于两个硅烯量子点之间的强耦合，能量共振点5.84 eV的诱导电荷密度类似一个大的偶极子，离域化的π电子可以在整个体系中来回运动，在量子点中原子实所在的位置，同样是由于σ电子的参与以及原子势的局域束缚，呈现相反的诱导电荷。由于量子点之间的强耦合，能量共振点14.77 eV的诱导电荷密度虽然也类似于两个偶极子，但是较多的诱导电荷分布在二聚物的两端。

图3　硅烯量子点二聚物间隙处依赖于共振频率的电流随着间距的演化过程Fig.3Current of silicene quantum dot dimers as a function of excitation energy and the gap distances

图5给出了沿平行于硅烯所在平面方向激发，不同间距D时，硅烯量子点二聚物的吸收光谱。其中，图5（a）和（b）中还分别给出了沿平行于硅烯所在平面方向激发时，单个矩形硅烯量子点的吸收光谱。沿如图1所示的扶手椅边界方向激发时，在5.5 eV以下，硅烯量子点二聚物的吸收光谱不但和单个硅烯量子点的吸收光谱线形一样，而且相应吸收峰的强度也基本一样。不过与单个硅烯量子点所不同的是，硅烯量子点二聚物相应吸收峰的位置发生了蓝移。这种结果和H型分子聚集体的相同。相对于单个分子，由于分子之间的偶极相互作用，H型分子聚集体的吸收光谱发生了蓝移25。在大于5.5 eV时，硅烯量子点二聚物的吸收光谱虽然和单个硅烯量子点的吸收光谱线形还基本一样，但是相应吸收峰的强度比单个硅烯量子点的大许多；同样，沿如图1所示的Z字形边界方向激发时，在6.1 eV以下，硅烯量子点二聚物吸收光谱的线形以及强度几乎都和单个硅烯量子点吸收光谱的一样。与单个硅烯量子点相比，硅烯量子点二聚物主要相应吸收峰的位置也发生了蓝移。在大于6.1 eV时，尽管线形还基本一样，但是硅烯量子点二聚物吸收光谱的强度也比较大。这是由于参与低能等离激元激发的主要是离域化的π电子18，沿平行于硅烯所在平面方向激发时，π电子在量子点平面两侧空间较大的范围内运动，对于一定的间距D，当两个硅烯量子点有一定耦合时，由于硅烯的低翘曲度结构，在间隙处沿平行于平面方向π电子的运动容易受到抑制；参与高能等离激元激发的主要是σ电子，由于σ电子在硅原子实附近运动，运动空间较小，所以在间隙处σ电子的运动几乎不受间距的影响。这种沿平行于硅烯所在平面方向激发的特性，与沿垂直于硅烯所在平面方向激发时的不同。在不同间距D，沿垂直于硅烯所在平面方向激发时，图2的结果表明，硅烯量子点二聚物各吸收峰的强度，分别约为单个矩形硅烯量子点相应吸收峰强度的两倍。这说明沿垂直于硅烯所在平面方向激发时，硅烯量子点二聚物参与各等离激元共振的电子数分别约为单个硅烯量子点参与相应等离激元共振电子数的两倍。此外，我们也用OCTOPUS软件，通过在频率空间求解Casida方程来计算了各个体系的吸收光谱26。在吸收光谱的变化趋势上，Casida方程的计算结果和含时演化波函数方法的计算结果基本是一致的。

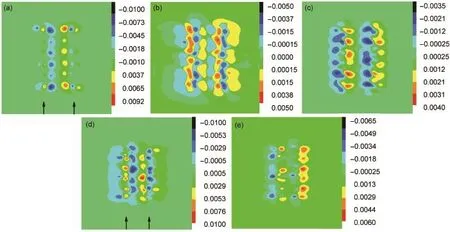
图4　沿如图1所示的x轴方向激发时，间距D为0.5 nm时，在等离激元能量共振点0.84 eV（a），6.15 eV（b）和14.86 eV（c）的傅里叶变换诱导电荷密度分布；间距为0.3 nm时，在能量共振点5.84 eV（d）和14.77 eV（e）的傅里叶变换诱导电荷密度分布Fig.4Fourier transform of the induced charge density for D=0.5 nm，to an impulse excitation polarized along x-axis direction as shown in Fig.1　，at the energy resonance points 0.84 eV（a），6.15 eV（b），and 14.86 eV（c），respectively；Fourier transform of the induced charge density for D=0.3 nm，at the energy resonance points 5.84 eV（d）and 14.77 eV（e）The position indicated by the arrow in figure is the position of atom in silicene quantum dots.The unit of the induced charge density is 1.6×1011C∙m－3.

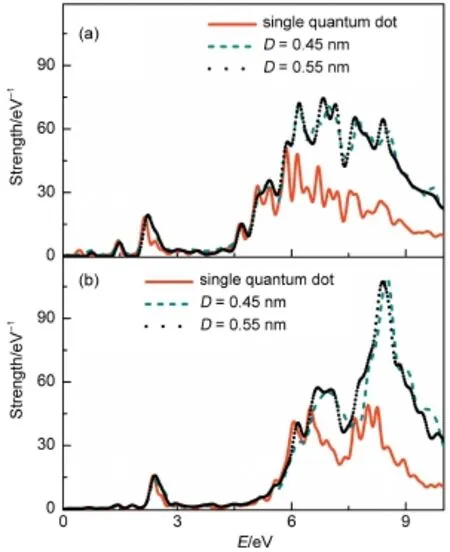
图5　分别沿如图1所示的y轴（a）和z轴（b）方向激发时，单个硅烯量子点和硅烯量子点二聚物的吸收光谱Fig.5Optical absorption spectra of single silicene quantum dot and silicene quantum dot dimers，to an impulse excitation polarized in the y-axis（a）and the z-axis（b）directions as shown in Fig.1　

为了进一步分析硅烯量子点二聚物等离激元的激发特性，图6给出了沿如图1所示各坐标轴方向激发时，自由硅烯量子点二聚物的吸收光谱。通过第一性原理进行结构优化，结果表明自由硅烯量子点二聚物中两个片层之间的距离平均为0.241 nm；在一个硅烯量子点中，上下两层硅原子之间的间距平均为0.004 nm，即每一个硅烯量子点呈近平面型结构，同以前的研究结果一致27，28。沿垂直于硅烯量子点平面x轴方向激发时，体系中有一个较大的等离激元共振带位于15 eV附近。与如图2所示间距较大时，硅烯量子点二聚物沿x轴方向的激发光谱相比，自由硅烯量子点二聚物在7 eV附近吸收峰的强度较弱。这一方面是由于自由硅烯量子点二聚物中每个量子点的低翘曲度导致的，另一方面是由于自由硅烯量子点二聚物中两个量子点之间的间距较小，沿x轴方向两个片层中相应的硅形成了共价键，导致了离域化的π电子数进一步减少。基于同样的原因，相对于间距较大的硅烯量子点二聚物，沿平行于硅烯所在平面方向激发时，在较低的能量区域，自由硅烯量子点二聚物吸收光谱的强度较弱。

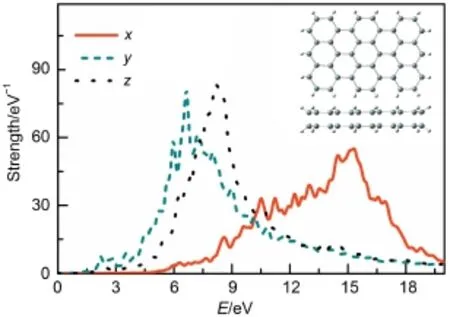
图6　分别沿如图1所示坐标系各坐标轴方向激发时，自由硅烯量子点二聚物的吸收光谱Fig.6Optical absorption spectra of free silicene quantum dot dimers，to an impulse excitation polarized in each coordinate axis directions as shown in Fig.1　The inset is the schematic diagram of free silicene quantum dot dimers （upper for top view，lower for side view）.

4　结论

采用含时密度泛函理论，本文主要研究了随着间距改变时硅烯量子点二聚物等离激元激发的演化规律。通过对计算结果的分析，得出以下主要结论。沿垂直于硅烯所在平面方向激发，当两个硅烯量子点间的间距较大时，硅烯量子点二聚物中有两个等离激元共振带，分别位于7和15 eV附近。随着间距的减小，当两个量子点之间由经典相互作用转变为量子相互作用时，7 eV附近的等离激元共振带一直发生红移；而高能共振区15 eV附近的等离激元共振带几乎不发生移动。这主要是由于参与15 eV附近等离激元共振激发的主要是σ电子，参与7 eV附近等离激元激发的大部分电子为离域化的π电子。此外，当两个量子点之间有一定的耦合时，在近红外光谱区0.6 eV附近，出现了长程电荷转移激发模式。随着间距的减小，该激发模式逐渐蓝移。当二聚物中两个量子点之间的耦合较强时，长程电荷转移激发模式消失。沿平行于硅烯所在平面方向激发，在两个量子点之间有相互耦合时，对于主要由离域化π电子参与激发的低能共振区，由于在间隙处沿平行于平面方向π电子的运动容易受到抑制，硅烯量子点二聚物吸收光谱的线形以及相应吸收峰的强度都和单个硅烯量子点吸收光谱的一样；而对于主要由σ电子参与激发的高能共振区，硅烯量子点二聚物相应吸收峰的强度约为单个硅烯量子点的二倍。

致谢：感谢武汉大学物理科学与技术学院徐红星教授在计算等方面给予的热心帮助。

References

（1）Novoselov，K.S.；Geim，A.K.；Morozov，S.V.；Jiang，D.；Zhang，Y.；Dubonos，S.V.；Grigorieva，I.V.；Firsov，A.A. Science 2004，306，666.doi:10.1126/science.1102896

（2）Novoselov，K.S.；Falko，V.I.；Colombo，L.；Gellert，P.R.；Schwab，M.G.；Kim，K.Nature 2012，490，192.doi:10.1038/ nature11458

（3）Xu，M.；Liang，T.；Shi，M.；Chen，H.Chem.Rev.2013，113，3766.doi:10.1021/cr300263a

（4）Liu，C.C.；Feng，W.X.；Yao，Y.G.Phys.Rev.Lett.2011，107，076802.doi:10.1103/PhysRevLett.107.076802

（5）Liu，C.C.；Jiang，H.；Yao，Y.G.Phys.Rev.B 2011，84，195430. doi:10.1103/PhysRevB.84.195430

（6）Chen，L.；Liu，C.C.；Feng，B.J.；He，X.；Cheng，P.；Ding，Z.；Meng，S.；Yao，Y.；Wu，K.Phys.Rev.Lett.2012，109，056804. doi:10.1103/PhysRevLett.109.056804

（7）Chen，L.；Li，H.；Feng，B.J.；Ding，Z.；Qiu，J.；Cheng，P.；Wu，K.；Meng，S.Phys.Rev.Lett.2013，110，085504.doi:10.1103/ PhysRevLett.110.085504

（8）Padova，P.D.；Vogt，P.；Resta，A.；Avila，J.；Razado-Colambo，I.；Quaresima，C.；Ottaviani，C.；Olivieri，B.；Bruhn，T.；Hirahara，T.；Shirai，T.；Hasegawa，S.；Asensio，M.C.；Lay，G.L.Appl. Rev.Lett.2013，102，163106.doi:10.1063/1.4802782

（9）Meng，L.；Wang，Y.L.；Zhang，L.Z.；Du，S.；Wu，R.；Li，L.；Zhang，Y.；Li，G.；Zhou，H.；Hofer，W.A.；Gao，H.J.Nano Lett. 2013，13，685.doi:10.1021/nl304347w

（10）Grigorenko，A.N.；Polini，M.；Novoselov，K.S.Nature Photonics 2012，6，749.doi:10.1038/nphoton.2012.262

（11）Tong，L.M.；Xu，H.X.Physics 2012，41，582.［童廉明，徐红星.物理，2012，41，582.］

（12）Wang，Z.L.；Chen，Z.；Tang，C.J.Physics 2012，41，648.［王振林，陈卓，唐超军.物理，2012，41，648.］

（13）Fang，Z.Y.；Zhu，X.Physics 2011，40，594.［方哲宇，朱星.物理，2011，40，594.］

（14）Mohan，B.；Kumar，A.；Ahluwalia，P.K.Physica E 2013，53，233.doi:10.1016/j.physe.2013.05.014

（15）Wu，J.Y.；Chen，S.C.；Lin，M.F.New J.Phys.2014，16，125002.doi:10.1088/1367-2630/16/12/125002

（16）Wu，J.Y.；Lin，C.Y.；Gumbs，G.；Lin，M.F.RSC Adv.2015，5，51912.doi:10.1039/C5RA07721D

（17）Van Duppen，B.；Vasilopoulos，P.；Peeters，F.M.Phys.Rev.B 2014，90，035142.doi:10.1103/PhysRevB.90.035142

（18）Yin，H.F.；Xiang，G.Z.；Yue，L.；Zhang，H.Acta Phys.-Chim. Sin.2015，31，67.［尹海峰，向功周，岳莉，张红.物理化学学报，2015，31，67.］doi:10.3866/PKU.WHXB201411211

（19）Zuloaga，J.；Prodan，E.；Nordlander，P.Nano Lett.2009，9，887. doi:10.1021/nl803811g

（20）Song，P.；Nordlander，P.；Gao，S.W.J.Chem.Phys.2011，134，074701.doi:10.1063/1.3554420

（21）Tsai，C，Y.；Lin，J.W.；Wu，C.Y.；Lin，P.T.；Lu，T.W.；Lee，P.T. Nano Lett.2012，12，1648.doi:10.1021/nl300012m

（22）Marques，M.A.L.；Castro，A.；Bertsch，G.F.；Rubio，A. Comput.Phys.Commun.2003，151，60.doi:10.1016/S0010-4655（02）00686-0

（23）Troullier，N.；Martins，J.L.Phys.Rev.B 1991，43，1993. doi:10.1103/PhysRevB.43.1993

（24）Ceperley，D.M.；Alder，B.J.Phys.Rev.Lett.1980，45，566. doi:10.1103/PhysRevLett.45.566

（25）Maiti，N.C.；Mazumdar，S.；Periasamy，N.J.Phys.Chem.B 1998，102，1528.doi:10.1021/jp9723372

（26）Jamorski，C.；Casida，M.E.；Salahub，D.R.J.Chem.Phys. 1996，104，5134.doi:10.1063/1.471140

（27）Bai，J.；Tanaka，H.；Zeng，X.C.Nano Res.2010，3，694. doi:10.1007/s12274-010-0032-6

（28）Liu，H.；Han，N.；Zhao，J.J.Phys.:Condens.Matter 2014，26，475303.doi:10.1088/0953-8984/26/47/475303

Plasmon Excitations in Silicene Quantum Dot Dimers

YIN Hai-Feng1，2，*
（1College of Physics and Electronic Engineering，Kaili University，Kaili 556011，Guizhou Province，P.R.China；2College of Physical Science and Technology，Wuhan University，Wuhan 430072，P.R.China）

The properties of plasmon excitations in silicene quantum dot dimers are investigated using timedependent density functional theory.Within a certain gap distance，a long-range charge transfer plasmon mode appears in silicene quantum dot dimers due to an impulse excitation polarized in the direction perpendicular to the quantum dot plane.The π electrons that participate in this plasmon excitation mostly move between the two quantum dots.This plasmon mode is blue-shifted as the gap distance decreases.Moreover，for different gap distances，two main plasmon bands appear，one around 7 eV and the other around 15 eV.In the low-energy region of the spectrum，for an impulse excitation polarized in the direction parallel to the silicene quantum dot plane，the shape of the absorption spectrum and the corresponding peak intensity of the silicene quantum dot dimers are both equivalent to those of a single silicene quantum dot，due to coupling between the two dots.

Plasmon；Silicene；Dimer；Time-dependent density functional theory

November 26，2015；Revised:March 22，2016；Published on Web:March 24，2016.

O641

［Article］10.3866/PKU.WHXB201603241www.whxb.pku.edu.cn

*Corresponding author.Email:yinhaifeng1212@126.com；Tel:+86-13885543969.

The project was supported by the National Natural Science Foundation of China（11464023），Innovative Talent Team of Colleges of Guizhou Province，China（［2012］06），andAtomic and Molecular Physics Key Disciplines of Kaili University，China.

国家自然科学基金（11464023），贵州省普通高等学校创新人才团队（黔教合人才团队字［2012］06号）和凯里学院原子与分子物理重点学科资助项目

©Editorial office ofActa Physico-Chimica Sinica