SAR雷达目标回波模拟系统构建方法研究*

顾振杰　刘　宇

(91336部队　秦皇岛　066000)

GU Zhenjie　LIU Yu

(No.91336 Troops of PLA, Qinhuangdao　066000)



SAR雷达目标回波模拟系统构建方法研究*

顾振杰刘宇

(91336部队秦皇岛066000)

论文针对SAR雷达测试需求，对SAR雷达回波模拟系统的构建方法进行了分析，并对关键技术进行了深入研究，以数字高程图(DEM)为基准源，并采用距离时域相干法进行目标回波的仿真；应用DSP+FPGA阵列实现目标回波系统函数的实时计算;对雷达发射信号和目标回波系统函数进行傅里叶变换后，进行卷积和数字正交混频，实现回波信号的相关性模拟。论文所提出的方法，可实现SAR成像雷达较大场景目标回波模拟，并可有效提高目标回波模拟的实时性。

目标回波; FPGA阵列; 系统函数; 卷积; 正交混频

GU ZhenjieLIU Yu

(No.91336 Troops of PLA, Qinhuangdao066000)

Class NumberTN219

1　引言

合成孔径雷达(SAR)是一种主动式微波遥感成像雷达,具有全天候、全天时、高分辨、宽测绘带等特点,在军事以及国民经济的各个领域都有很广泛的应用[1～2]。随着技术的不断进步，SAR成像雷达变得越来越先进，越来越复杂，这也对SAR回波模拟器的建设提出了越来越高的要求[3]。

目前国内已建成一些SAR回波模拟器，大多采用高性能工作站、分布式计算、DSP、GPU等较为传统的计算方式来完成回波场景计算，模拟场景普遍不大，且多为回放式的非实时系统。随着对模拟地面场景大小要求不断提高、模拟实时性和真实性要求不断增加，目前多采用FPGA阵列来实现回波场景的实时模拟[4]。尽管FPGA存在器件成本高、开发周期较长、开发工具不易使用、开发人员要求较高等缺陷，但由于其具备单片多达超过2000个的DSP单元、灵活可配置的复杂逻辑功能、大带宽低延迟的数据互联能力，目前已成为实时SAR回波模拟计算所采用的最好手段。

本文所构建SAR成像回波模拟系统，利用数字高程图(DEM)[5～6]模拟真实反射场景的三维地物结构，构造目标模型，采用距离时域相干法[7]进行目标回波的仿真，应用DSP+FPGA阵列实现目标回波系统函数(用于表征SAR成像雷达目标回波特性)的实时计算。应用本系统，可实现SAR雷达较大场景目标回波的实时模拟，满足SAR雷达测试需求。

2　系统组成

SAR成像雷达回波模拟系统主要包括两个功能子模块：一个是系统函数实时计算模块，用来实现SAR目标回波系统函数的实时计算功能；另一个是信号调制模块，用来实现雷达信号的变频、采集以及雷达信号与目标回波系统函数的卷积、调制以及基带信号的上变频等功能。

系统函数实时计算模块主要由信号预处理DSP板组成和系统函数计算FPGA阵列。信号预处理DSP板用于对系统函数计算阵列的每个计算单元的任务进行划分、计算相应的仿真参数。系统函数计算FPGA阵列是SAR目标回波实时计算系统的核心，它用于计算目标回波系统函数(用于表征SAR成像雷达目标回波特性)。系统函数计算阵列由多块高性能计算板卡组成，每块板卡包含多片FPGA。

信号调制模块首先对雷达发射信号进行下变频，经过AD变换后在中频上对雷达信号进行采集，工程上一般采用专用的信号采集板来完成。然后在中频上对目标回波系统函数与雷达信号进行卷积和数字正交调制处理，在中频上生成雷达回波信号，然后经过DA变换和上变频后输出与雷达发射信号同频段的回波信号。

图1　系统功能组成图

3　SAR目标回波仿真算法

在SAR目标回波仿真中，最具代表性的仿真算法包括距离频域脉冲相干法、距离时域脉冲相干法以及二维频域快速傅里叶变换法等三种。为了满足SAR目标回波实时计算的要求，并在保证仿真数据真实性的同时尽量减少计算量，模拟器采用距离时域脉冲相干法进行目标回波的仿真。

SAR目标回波是雷达照射波束内全部散射点回波的叠加，它可以看作是雷达发射信号经过一个系统后的输出。因而SAR目标回波可表示为雷达发射脉冲s(t)与目标回波系统函数h(t)的卷积，即[8]

sr(t)=s(t)⊗h(t)

(1)

式中的系统函数包含了波束照射范围内所有散射点回波的延迟、幅度以及方位相位等信息，它可表示为

(2)

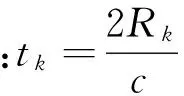
雷达发射脉冲信号为

(3)

将式(2)和式(3)代入式(1)后，得到面目标回波信号模型。由式(2)可知，目标回波系统函数是一系列冲击函数的叠加，这些冲击函数具有不同的延时、幅度和相位，其作用就是对雷达发射信号进行延迟、幅度和相位的调制。在距离时域脉冲相干法中，将根据目标回波系统函数的采样周期对散射点的延迟进行近似处理。此时在某个采样时刻的回波系统函数将是落入该时刻所代表距离门的所有散射点信息的叠加，即

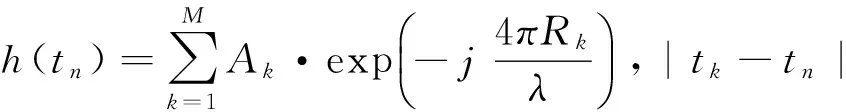
(4)

式中：M为落入该距离门散射点的个数，Ak、Rk和tk分别表示该距离门内第k个散射点回波的幅度、距离和延迟，Ts为系统函数的采样周期。

由于雷达波束在地面照射范围内的散射点数目非常多，因而在SAR目标回波仿真中，目标回波系统函数的计算量将非常大。

4　目标回波系统函数生成

目标回波系统函数表征SAR雷达目标回波的特性，在SAR目标回波计算中，目标回波系统函数是计算量最大也是最复杂的一个环节。它要对雷达地面照射范围内所有散射点回波的延迟、相位以及幅度等信息进行计算，并对处于同一距离门的回波信息进行累加。目标回波系统函数的实时计算可采用FPGA计算阵列来完成，这一方面由于FPGA本身具有丰富的资源适用于高性能计算，另外SAR目标回波仿真的特点也使得它能够通过多个计算单元的并行计算来完成[9]。

在利用FPGA阵列实时计算目标回波系统函数时，需要实时根据雷达波束范围对FPGA阵列中的每个计算单元进行计算任务的分配及参数设置，以便整个计算阵列系统能够协同工作，这项任务由DSP信号预处理板来完成。

从基准源角度来看，目前主要有两种：一种是通过数字高程图(DEM)模拟来模拟雷达回波数据，称为几何模型法。此方法可以真实地模拟三维场景以及雷达图像特有的几何畸变现象，运用比较广泛，模拟的回波更加真实可靠。另一种是灰度模型法。此方法虽然不能模拟雷达图像特有的几何畸变现象，但是可以作为几何模型方法的参考，作为几何模型方法的补充配准图像。本文中系统回波函数生成采用DEM方法。

系统回波函数实时计算过程如下：

1) 根据弹道信息和当前脉冲时刻递推得到当前雷达坐标、姿态以及雷达波束覆盖地图范围。在FPGA阵列中，此项功能可充分利用内嵌CPU进行计算。

根据雷达坐标和地面反射系数矩阵中心值计算方位角、俯仰角和高度值。

2) 从数字高程地图文件中读取当前脉冲时刻雷达波束照射的地图数据。地图数据在仿真前下载到外部存储器，该存储器一般采用高速同步SRAM介质。

3) 坐标转换。根据每个像元在大地坐标系下的坐标转换为天线坐标系下的坐标值，并计算每个像元到雷达的距离。此步骤利用定制可编程处理器实现，每个节点的处理器根据单个像元坐标位置和雷达坐标位置计算之间距离，为保证回波相位精度，需要采用双精度格式进行计算。

4) 根据天线方向图，对每个角度单元中的有效像元的后向散射系数进行幅度调制。

5) 根据距离值，计算每个像元对应的延迟单元和相位值；此步骤利用定制可编程处理器实现，延迟单元及相位值可采用查表法获取。

对于延迟单元，有dbin=Rif/fs，其中fs代表一个采样点所代表的距离。

对于相位值，有φij=4πRij/λ，其中为λ载波波长。

6) 根据地图数据，计算每个像元对应的幅度值Aij。

7) 根据每个像元的延迟单元、相位值和幅度值得到每个像元的冲激响应，即hij=Aij·φij；此步骤利用定制可编程处理器实现。

8) 根据每个像元的冲激响应，累计相加得到系统响应函数。

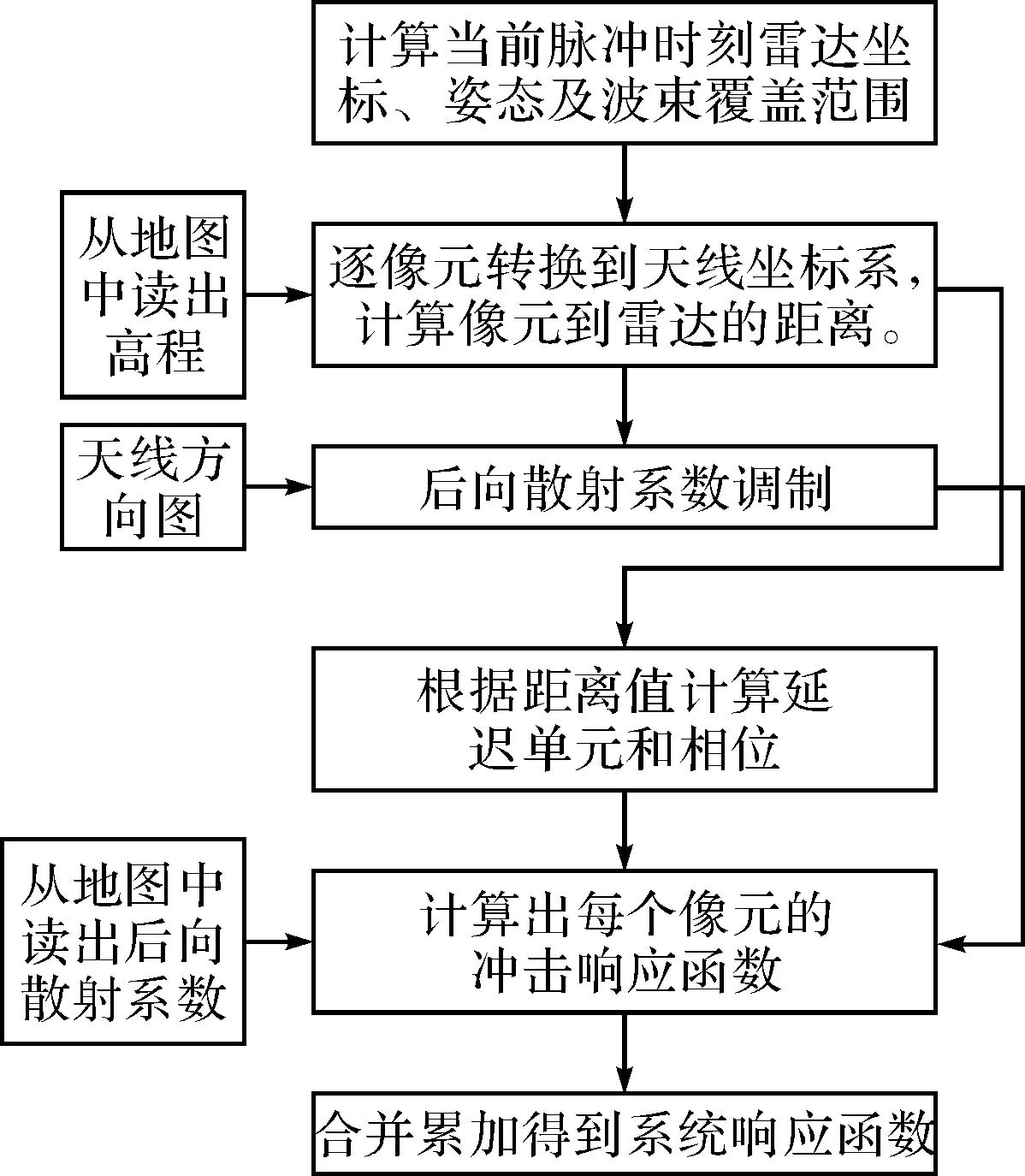
图2　系统响应函数计算流程

5　卷积及数字正交调制处理

目标回波系统函数与雷达基带信号进行卷积处理之后，将得到SAR目标回波基带信号。由于目标回波系统函数及雷达基带信号采样点数都很多，为了减少计算量，卷积将在频域完成。即通过信号在频域的相乘来实现其在时域的卷积。为了实现频域卷积，需要进行FFT及IFFT处理，利用FPGA自带的强大FFT核比较容易实现快速卷积运算，以便满足实时计算的要求。考虑到雷达信号波形在仿真中的变化，频域卷积中雷达信号的FFT数据也要根据雷达波形的改变进行调整。

快速卷积处理的运算表达式及基本流程如下：

sr(t,ta)=IFFT(FFT(s(t))×FFT(h(ta))

(5)

如图3所示，将线性调频信号预先变换到频域，将该频域数据存储在FPGA的RAM中，在进行快速卷积运算时直接从RAM中读取数据。复数乘法运算完成后，在RAM中截取前1024点和后1024点数据除去镜频，然后分时复用FFT核，实现IFFT运算。这样快速卷积运算多调用了一个RAM而少调用一个FFT核。通过分析可知，一个深度为2048点，位宽3bit的截取RAM、占用的逻辑资源远小于2048点的FFT所占用的资源[10]。

最后，对目标回波基带信号进行内插、数字正交调制以及DA变换等处理，将得到中频目标回波。由于模拟正交调制中两个通道信号的幅相不一致将会形成较大的镜像干扰，为此采用数字正交调制的方法进行上变频变换。由于上变频后信号的采样频率需要提高，因而在数字正交调制前进行内插处理，以提高信号的采样率。

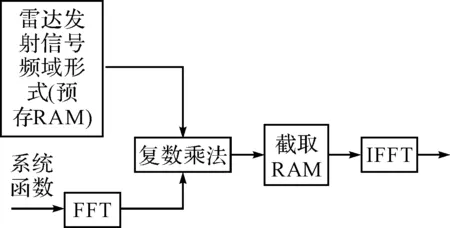
图3　快速卷积运算流程

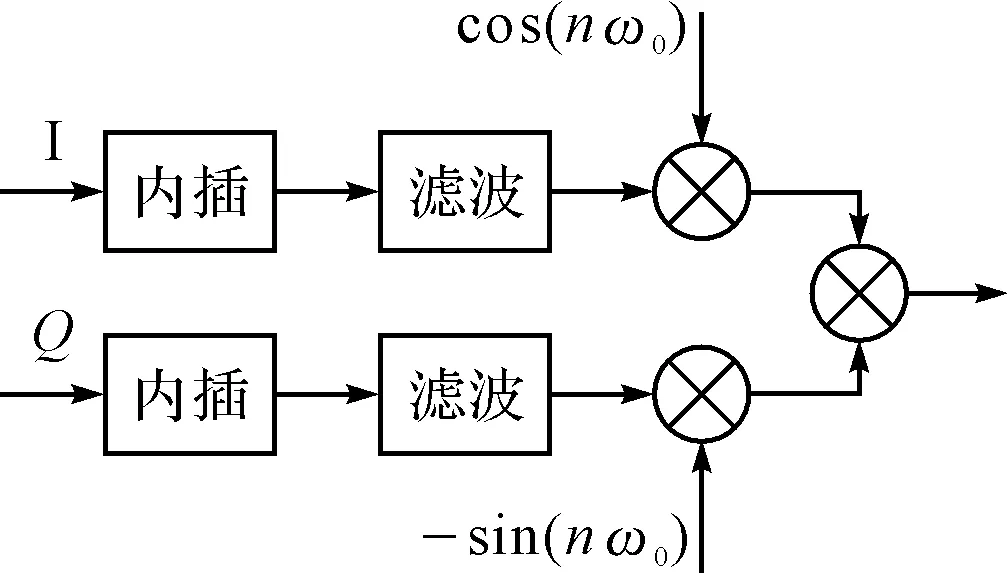
图4　正交调制原理图

雷达发射信号为

s(t)=a(t)cos(ϖ0t+θ(t))

(6)

经AD采样后，变成数字信号：

s(n)=a(n)cos(ϖ0t+θ(n))

(7)

其中，n=k/fs，k=0，1，2…。

通过混频技术，可得到信号的正交变量，数字信号正交混频的I路可表示为

s(n)cos(w0n)=1/2a(n)[cosθ(n)+cos(2w0n+θ(n))]

(8)

Q路可表示为

s(n)(-sin(w0n))

=1/2a(n)[sinθ(n)+sin(2w0n+θ(n))]

(9)

6　实验结果

本文所阐述技术在工程实践中得到了应用，在实验室条件下应用某型采用了本文所阐述技术的系统进行了验证实验。图5为利用安捷伦公司生产的E8257D信号源模拟产生具有一定带宽的线性调频信号，信号通过模拟系统进行相关调制后，应用安捷伦公司生产的DSO80604B示波器对信号的时域信息进行测量，如图所示为在通过系统调制后产生的距离扩展信号，信号在基带测量，扩展点数为16点，各扩展点之间具有相对的幅度起伏关系，反映了各扩展点不同的回波特性。

图5　时域分布示意图

图6和图7为系统所成海岛场景和舰船图像，图像采用系统自带软件显示，数据场景大小为300*300点，由图可见，所成图像较为准确地反映了目标场景的回波信息。

图6　海岛成像图

图7　舰船成像图

7　结语

本文对SAR成像雷达目标回波模拟系统的构建方法进行了研究，对SAR目标回波仿真算法、目标回波系统函数生成和卷积及数字正交调制处理等三项关键技术进行了深入分析，并给出了具体的应用实例。本文所采用技术在国内具有一定的先进性和代表性。尤其是采用DSP+ FPGA阵列的方式实现目标回波系统函数的实时计算，可很好地实现较大场景和高实时性回波信号的模拟。但采用该方法，尤其是采用大规模FPGA阵列，虽然效果很好，但造价很高。因此，在进行相关系统设计时，要综合考虑应用需求与成本之间的关系，选取合理的建设方式，以取得最佳的效费比。

[1] 张澄波.综合孔径雷达原理、系统分析与应用[M].北京：科学出版社,1989：3-10.

[2] 段秋萍,董戈.基于真实场景的SAR回波模拟方法研究[J].遥测遥控,2007(5):36-40.

[3] 孟献柯,朱峰.基于Creator/Vega的合成孔径雷达图像仿真[J].舰船电子工程,2014(1):36-40.

[4] 王虹现,全英汇.基于FPGA的SAR回波仿真快速实现方法[J].系统工程与电子技术,2007(11):2284-2289.

[5] 金玉荣.星载SAR信号仿真研究[D].长沙：国防科学技术大学,2006：1-6.

[6] 吴广志,李仁龙.SAR导引头中制导地面场景RCS计算[J].雷达科学与技术,2010(12):516-520.

[7] 林江红,浮瑶瑶.面向应用的SAR场景回波信号仿真质量评估方法[J].现代雷达,2013(2):68-72.

[8] 陆智俊.宽带雷达目标射频仿真及其应用[J].上海航天,2009(3):59-63.

[9] 吕海涛.SAR雷达模拟成像技术研究[J].舰船电子工程,2010(5):70-73.

[10] 易永军,宗竹林.一种基于FPGA的自然场景的实时SAR回波模拟器[J].现代雷达,2013(2):13-17.

Construction Method of SAR Radar Target Echo Simulation System*

Aimed to the requirement of the SAR radar testing, the construction method of SAR Radar target echo simulation system is analyzed, and the key technology is researched deeply.The target echo is simulated by using the coherence method of distance time domain based on standard source. The target echo system functionrealizes real-time calculating by using DSP +FPGA array. The echo signal correlation simulation is realized by convolved and digital quadrature down-convert after radar transmit signal and target echo system function in Fourier transform. The simulation of the large scene of SAR imaging radar is realized, and the real-time performance of target echo simulation is improved effectively.

target echo, FPGA array, system function, convolve, orthogonal mixing

2016年2月8日,

2016年3月27日

顾振杰,男,高级工程师,研究方向：射频仿真。刘宇,男,硕士研究生,工程师,研究方向：射频仿真。

TN219

10.3969/j.issn.1672-9730.2016.08.025