基于脉冲角度特征的雷达辐射源识别及仿真实现*
谭 龙 潘继飞 杨 丽 吴惟诚
(电子工程学院信号与信息处理实验室 合肥 230037)
TAN Long PAN Jifei YANG Li WU Weicheng
(Laboratory of Information Processing, Electronic Engineering Institute, Hefei 230037)
基于脉冲角度特征的雷达辐射源识别及仿真实现*
谭龙潘继飞杨丽吴惟诚
(电子工程学院信号与信息处理实验室合肥230037)
针对目前雷达告警系统中对雷达辐射源识别精度不高的问题,提出利用一类新的指纹特征——脉冲角度特征进行辐射源识别。为能得到较精确的脉冲角度特征,在利用Hilbert法提取脉冲包络的基础上,对包络曲线进行三次样条拟合,并证明了由此所提脉冲角度特征的良好聚类性,最后,通过实例仿真验证了利用该特征能较好对辐射源信号进行分类识别。
指纹特征; 脉冲包络; 角度特征; 辐射源识别
TAN LongPAN JifeiYANG LiWU Weicheng
(Laboratory of Information Processing, Electronic Engineering Institute, Hefei230037)
Class NumberTN95
1 引言
目前用于雷达辐射源识别的常用脉冲包络“指纹”特征[1]有:脉冲包络形状、脉冲包络的高阶矩特征、脉冲包络的一阶差分特性等,其中基于脉冲包络形状进行“指纹”识别的方法,在文献[2]中有具体论述,该方法首先利用雷达知识库中已有的信号参数,生成若干包络的模板作为先验知识,然后对截获的未知信号进行模板匹配,从而通过相关系数判断信号属于哪种雷达,该方法计算简单、速度快,但该方法也受时域波形的影响较大,易被噪声、信道干扰;文献[3]详细介绍了一类基于脉冲包络高阶矩特征的识别,则是利用信号的Hilbert变换,计算截获信号的四阶矩特征,然后利用高阶矩特征的聚类型判断雷达的类型,该方法能够抑制高斯噪声的影响,具有较好的稳定性,但计算量较大,不易进行工程实现。
经过上面的分析可知,在“指纹”特征中,信号的包络特征主要指信号参数特征,其特性主要取决于雷达发射机、传播路径、截获接收机。对其进行描述时,一般选择时域参数,主要包括:脉宽、脉冲上升/下降沿时间、顶降、尖峰位置及其幅度等。本文对一类新的“指纹”特征——脉冲角度特征进行了研究,下面对其定义、提取方法及在辐射源识别中的运用进行具体介绍。
2 脉冲包络提取
2.1信号滤波
为能得到较纯净的辐射源信号,从而取得理想的、可靠的脉冲包络,告警接收机首先需对所截获信号进行滤波处理。目前使用较多的滤波算法有算术平均值滤波法、中值判断法、加权滤波法、滑动滤波法等,这几类滤波算法原理简单,但处理后数据的精度不高,本文采用巴特沃斯滤波器(Butterworth Filter)对信号进行滤波[4]。
巴特沃斯滤波器是无限冲击响应(IIR)滤波器的一种,最大的特性是通带和阻带都有平坦的幅度响应,其幅度平方响应具有如下形式:
(1)
式中:wc为截至频率(rad/s),N为滤波器阶数,通带的近似性和过渡带的陡峭性都和N的取值有关,N越大性能越好,越接近理想的矩形滤波器。
模拟巴特沃斯低通滤波器的系统传递函数为
(2)
式中阶数N为偶数,说明巴特沃斯滤波器可写成N/2个2阶级联的形式,用下式将其转化为数字滤波器:
(3)
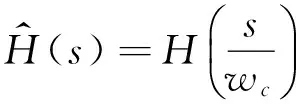
这是巴特沃斯低通滤波器的幅度和频率响应,在设计带通滤波器时,只需将其中心频率根据需要进行适当的变换,并根据截获信号设置适当的带宽和衰减系数,便能得到理想的带通滤波器。设截获信号为s(t),滤波器冲击响应为h(t),则系统函数H(w),滤波后的输出信号为
y(t)=f(t)*h(t)
(4)
2.2利用Hilbert法提取信号包络

2.3脉冲包络的曲线拟合
直接利用Hilbert得到的信号包络,由于受到噪声、信道衰落、多径效应等的影响,得到的包络形状不尽理想,给后续角度特征的提取造成极大影响。考虑到这个问题,为得到可靠的、更合乎实际的包络曲线,本文采用三次样条插值法对用Hilbert得到的包络曲线进行拟合。
样条法是通过构造多项式(一个或一组不同阶多项式)来形成一条平滑曲线对各主干点进行拟合,工程上一般选用三次曲线(三次插值样条函数的曲线),其定义如下:
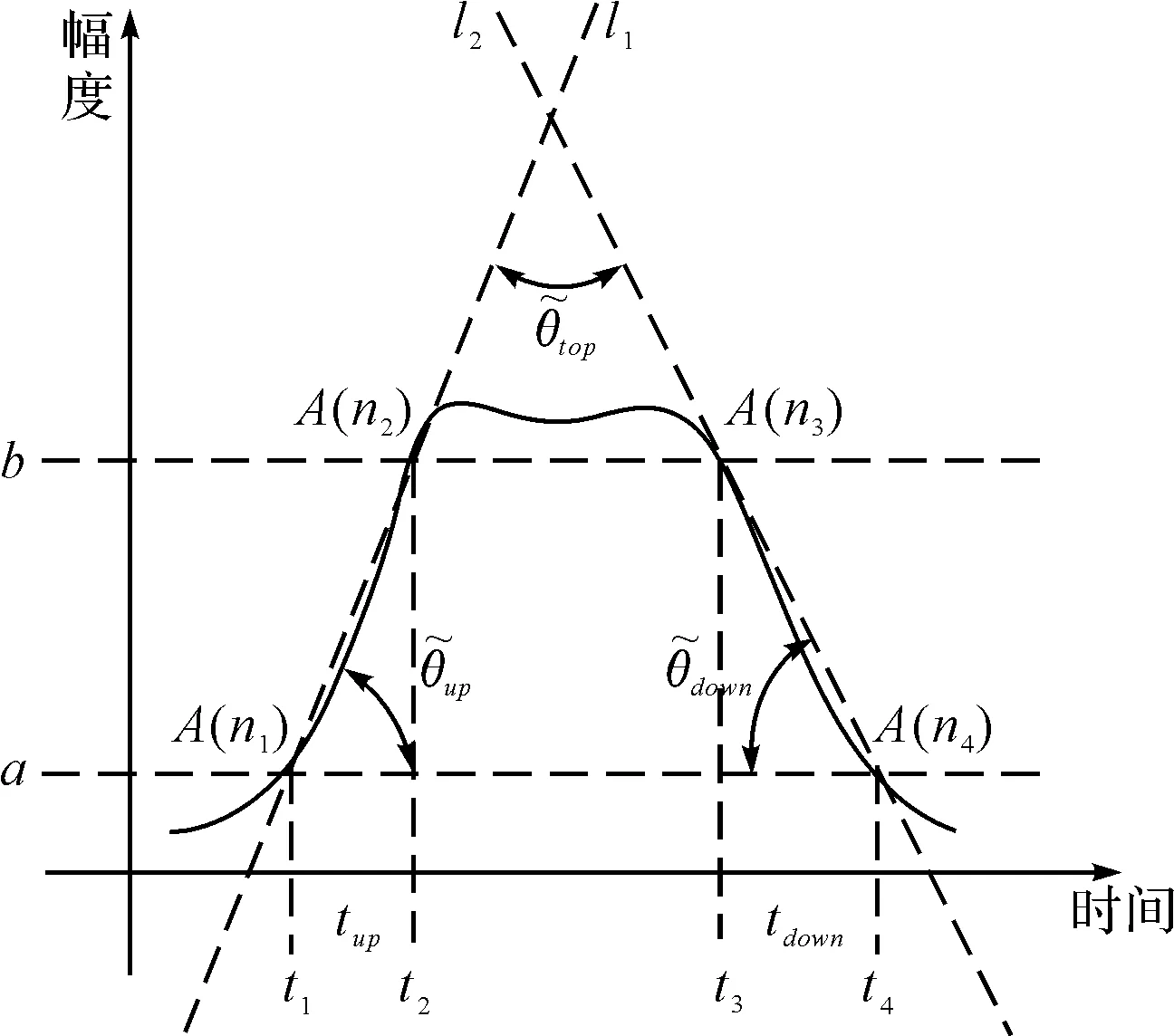
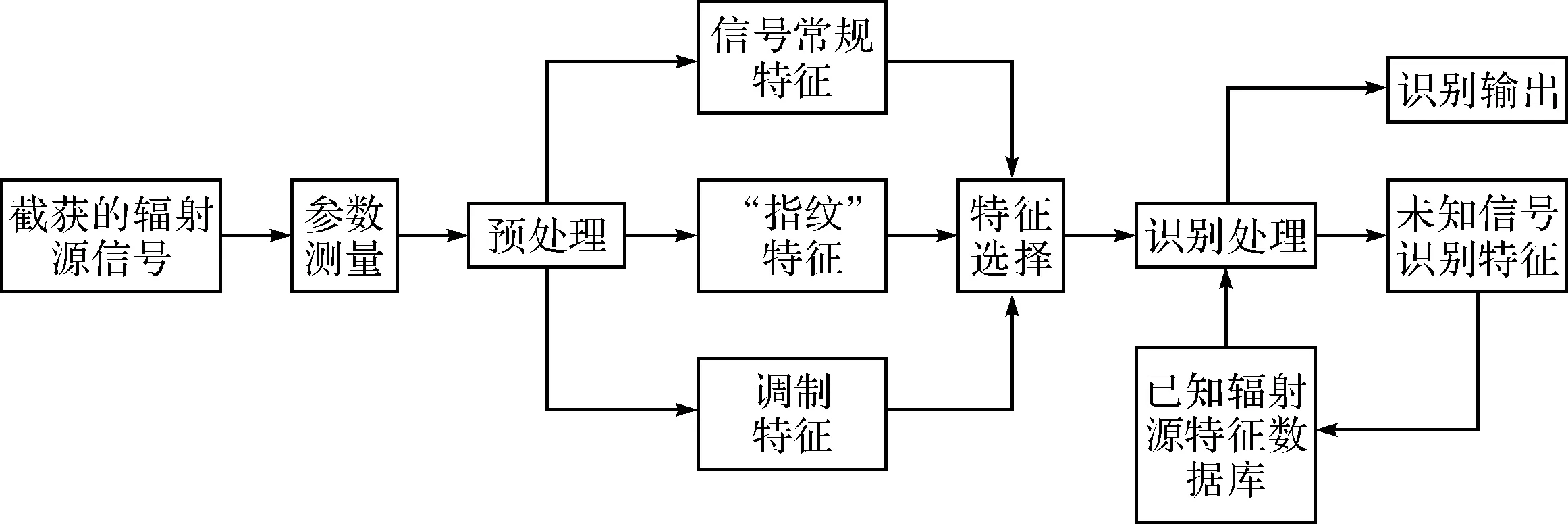
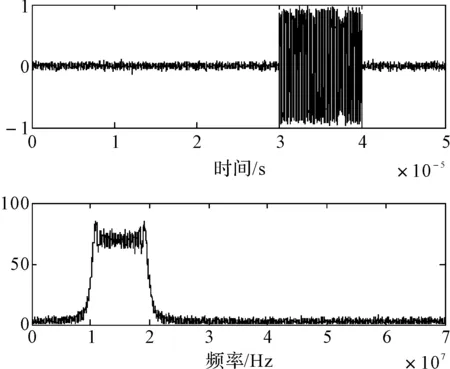
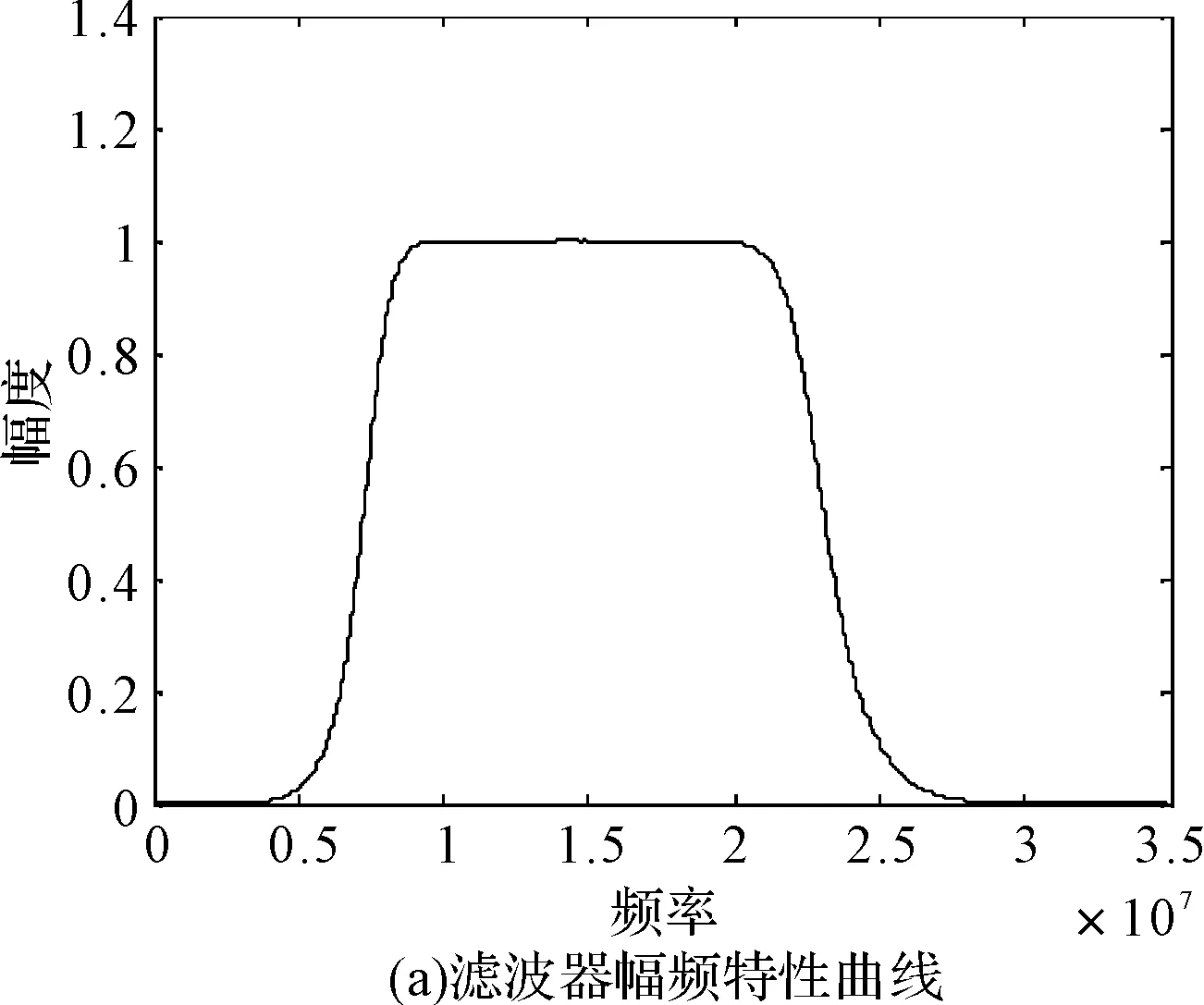
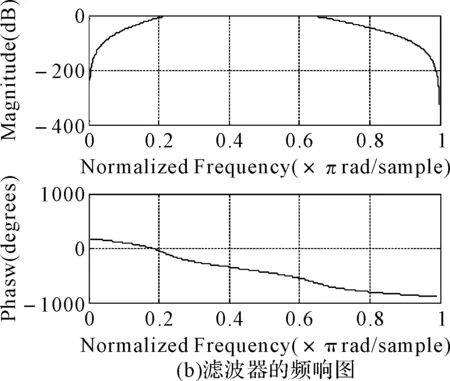
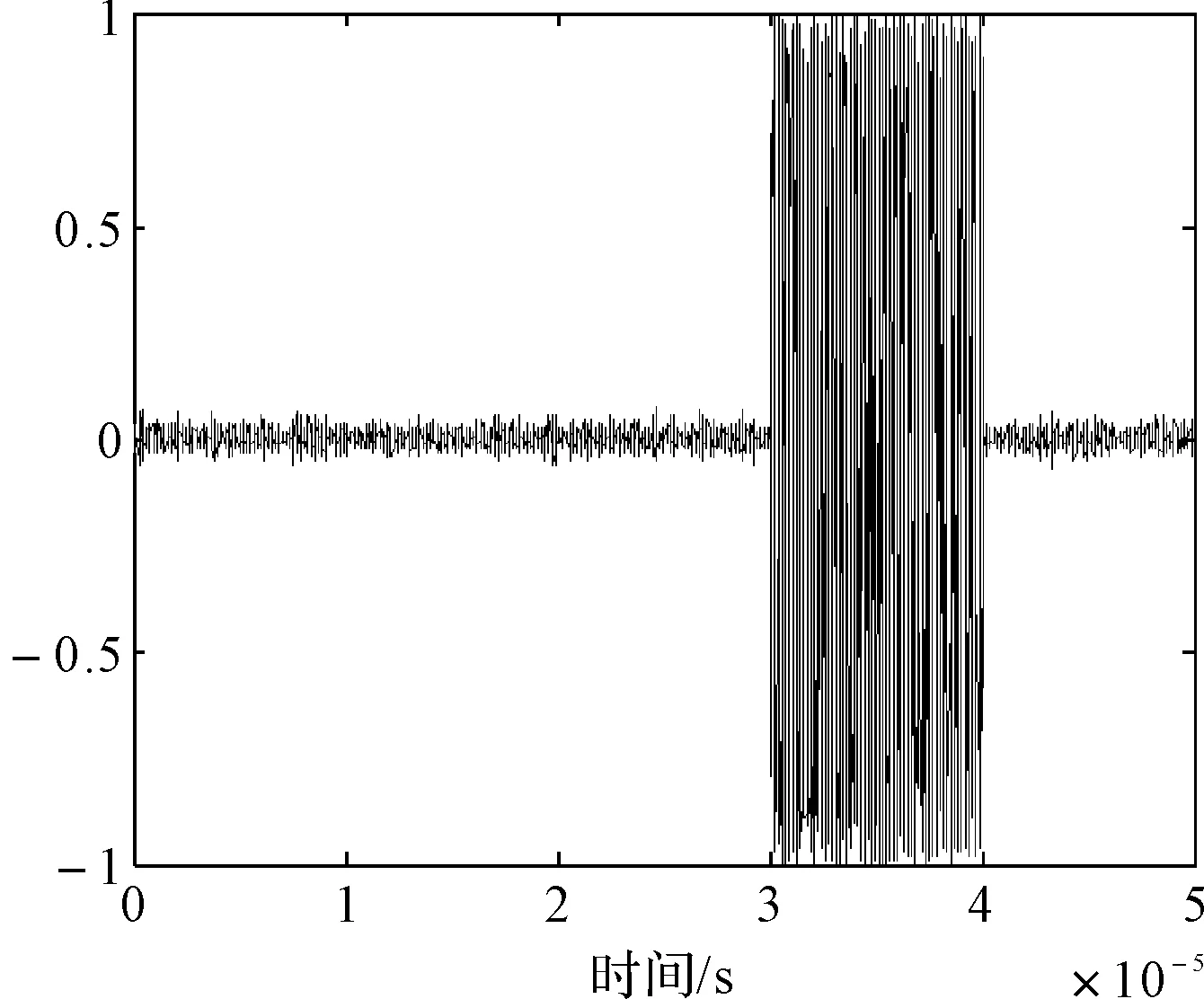
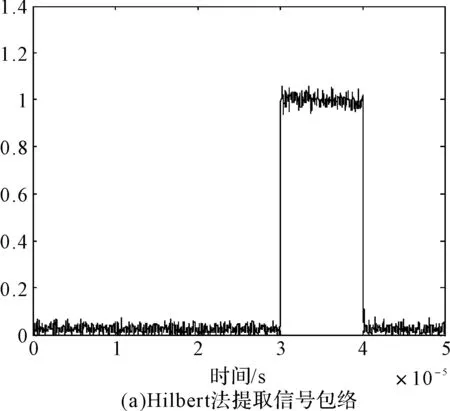
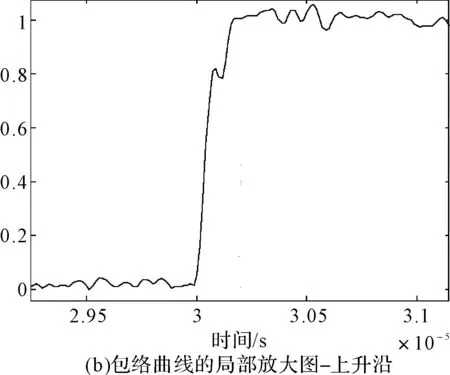
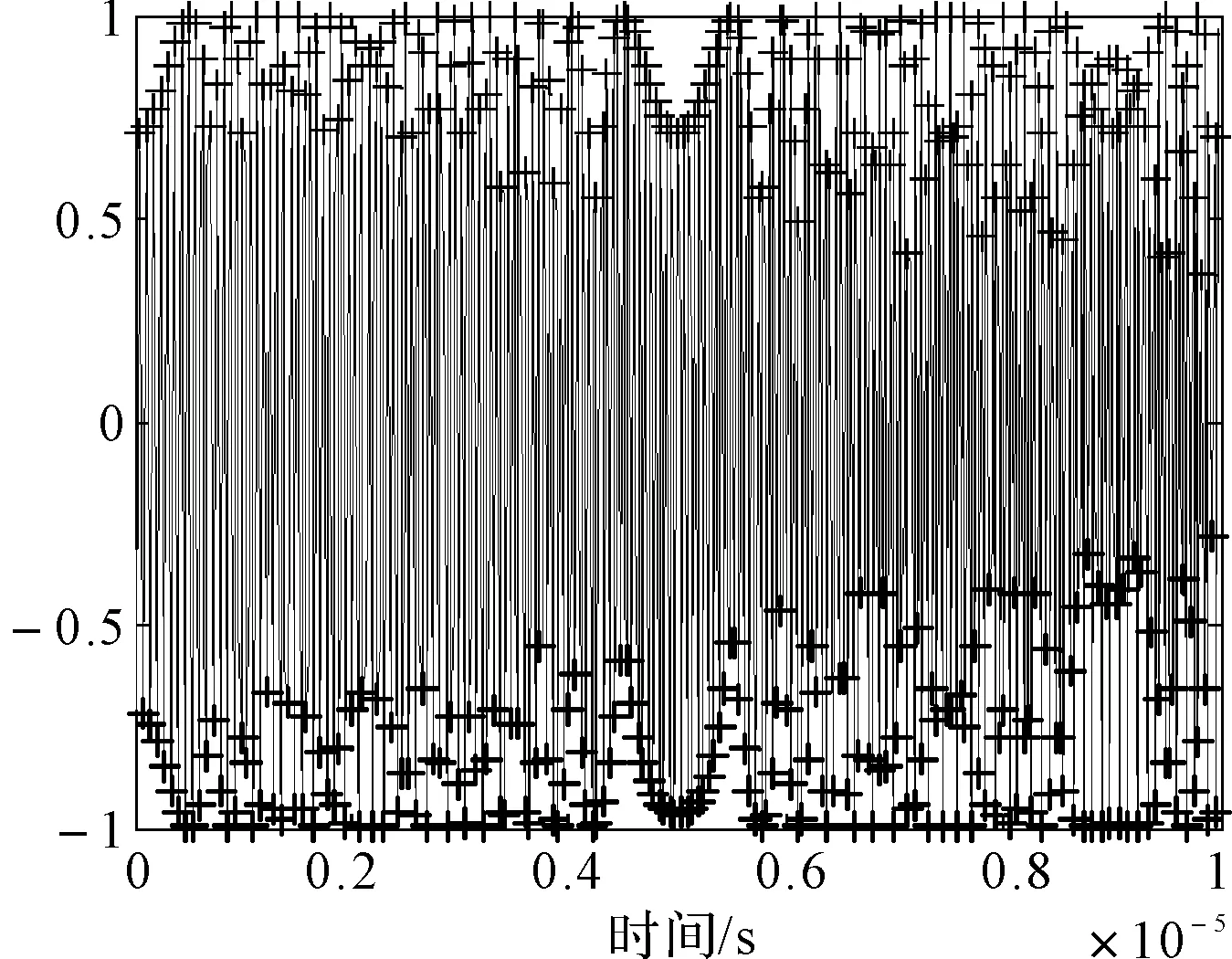
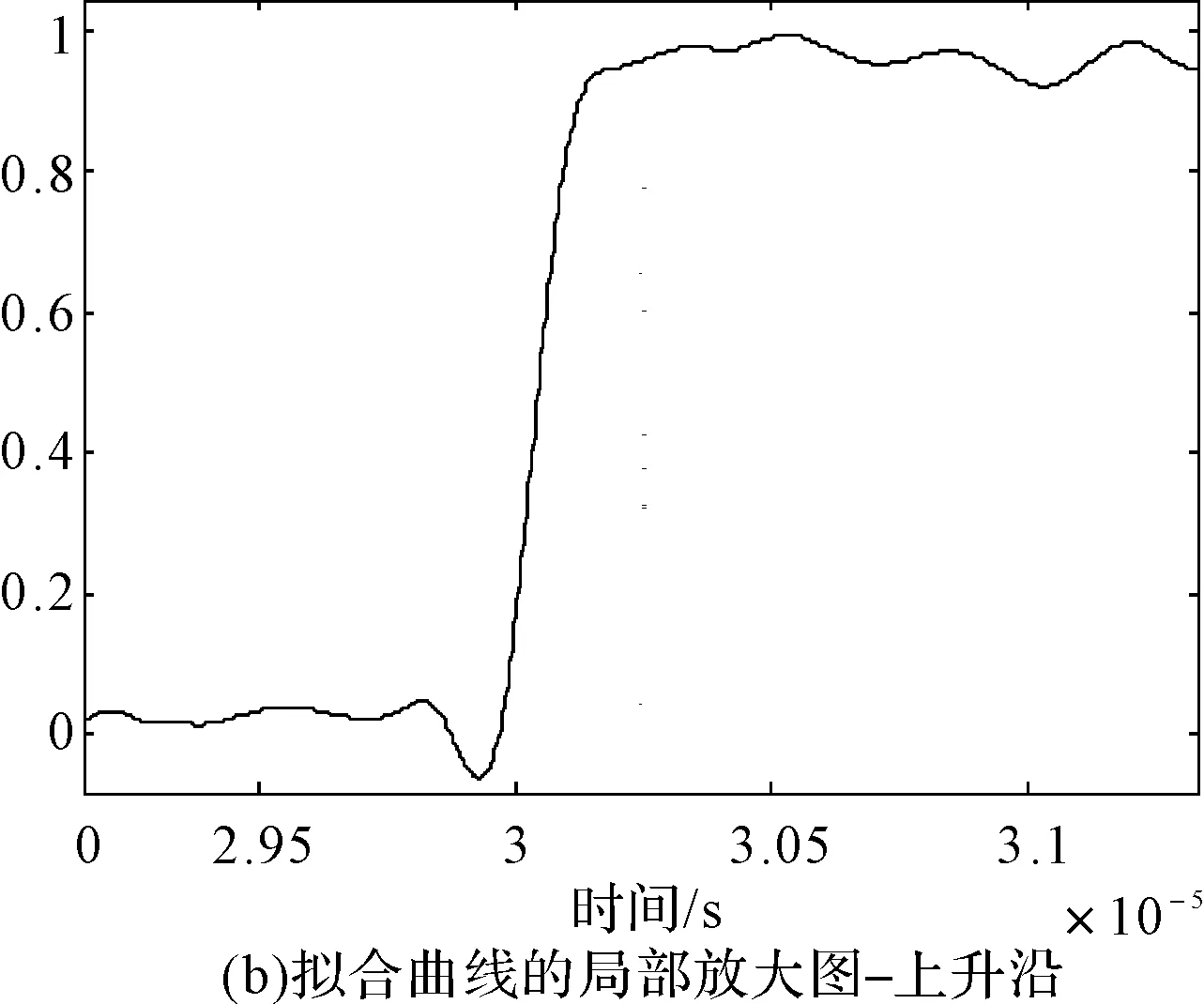
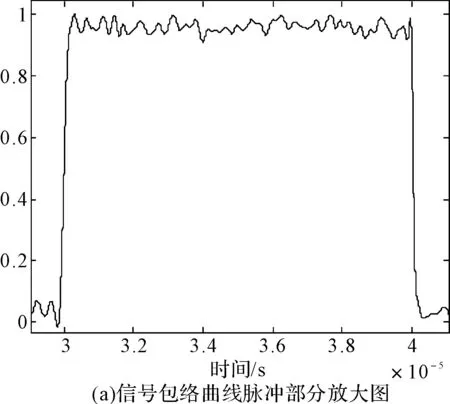
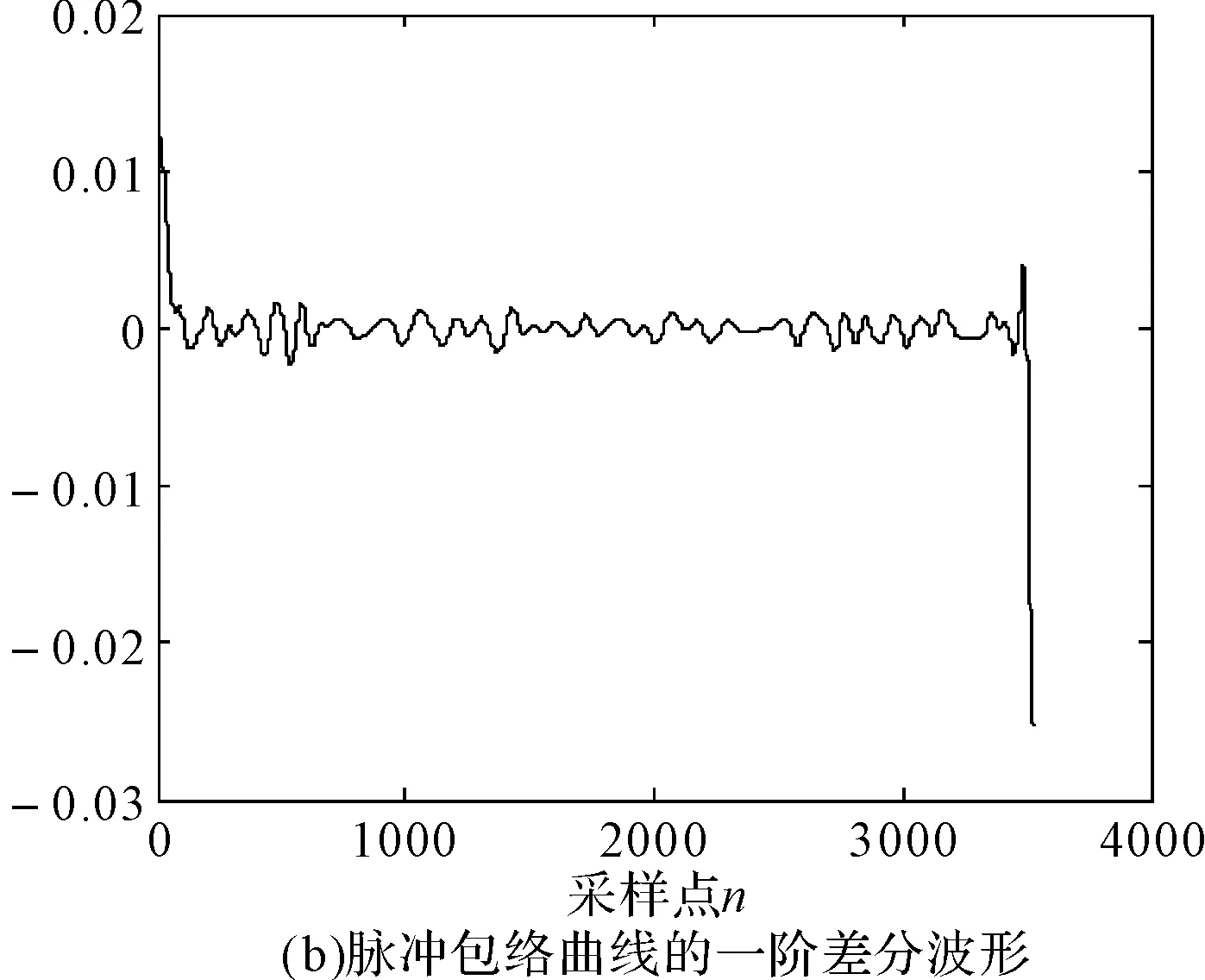
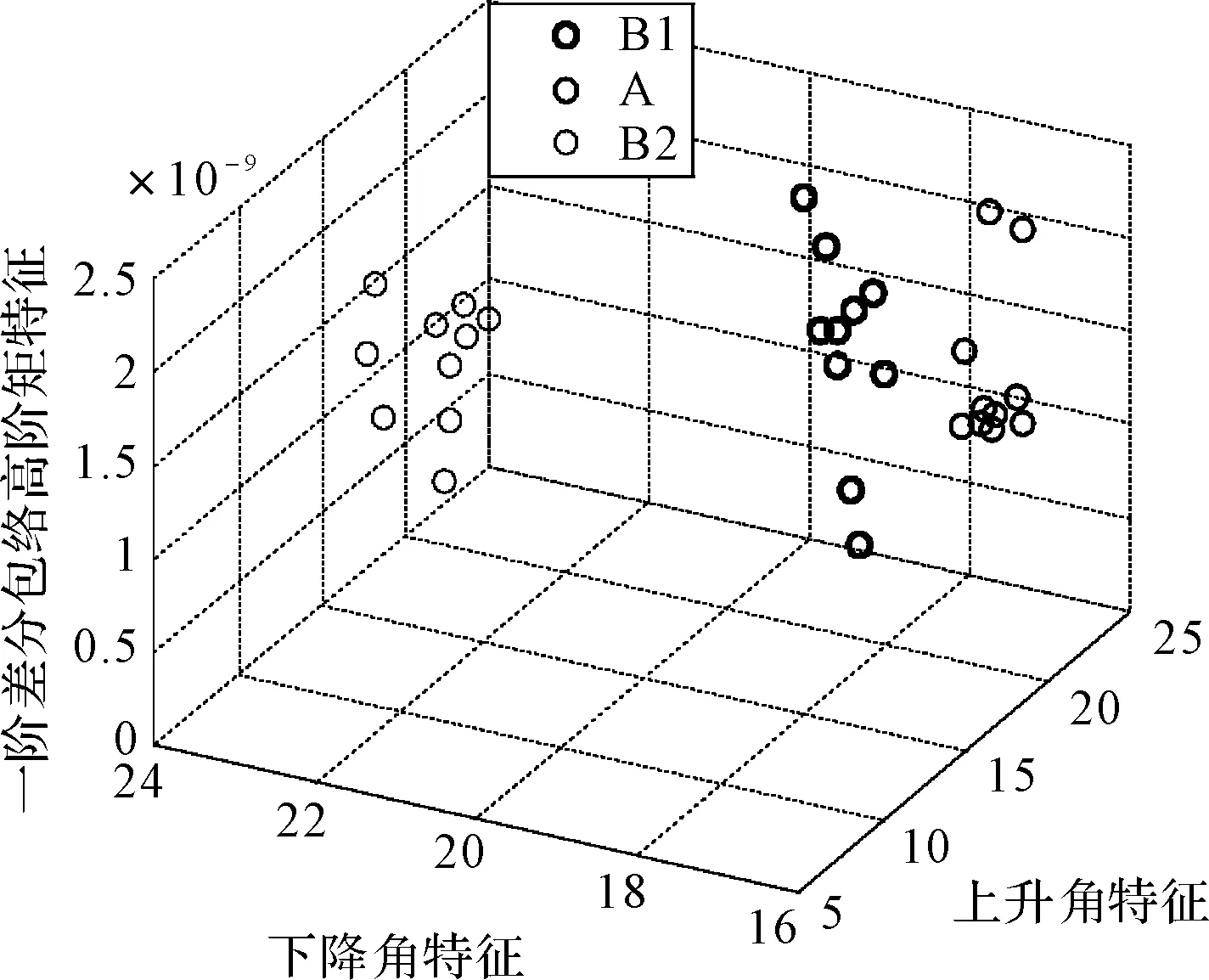
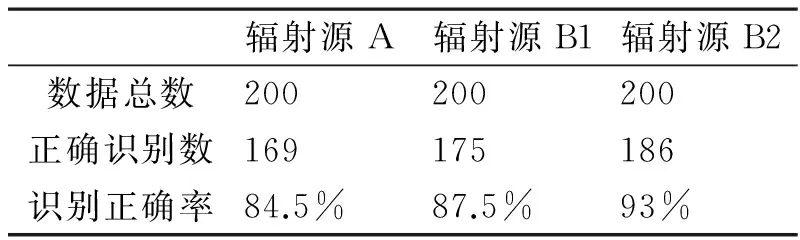
在给定区间[a,b]上,以ti(i=0,1,2,…,n)为节点的一个划分δ为a=t0 1)一致通过n+1个插值点(ti,hi),即S(xi)=f(xi)=hi(i=0,1,2,…,n); 2)二阶连续,即S(x)∈C2[a,b]; 3)三次分段,即每一个小区间[ti-1,ti],(i=0,1,2,…,n)上均为三次多项式。 则称S(x)为f(x)的三次样条插值函数,在确定S(x)应该根据n+1个插值条件,3n-3个连续条件以及给定的边界条件,再利用节点处的一阶导数或二阶导数就可构造出三次插值样条函数。 由理论分析可知,函数S(x)是通过分段三次多项式逼近y=f(x),且满足上诉三个条件,故三次插值样条函数具有优良的数学特性。同时,利用Matlab中现有的工具箱,可以灵活设计插值函数,且便于实现[6~7]。 在得到信号包络的基础上,首先给出脉冲角度特征如图1所示。 1)为准确提取脉冲包络中的角度特征,首先对上文定义的脉冲包络A(t)进行离散化处理,记为A(n),则包络的一阶差分记为 A1(n)=A(n)-A(n-1)n=1,2,3,…,N-1 (5) (6) (7) 3)再由三角函数公式,即可求得脉冲上升/下降沿的角度特征信息: (8) 需着重说明的是,由本文定义提取的脉冲角度特征信息,并非传统的角度值,而是由角度信息反映的一定数据值。 图1 雷达脉冲特征提取示意图 首先给出雷达辐射源识别模型如下。 图2是目前使用较多的识别系统,该套系统能过针对不同的功能需要,提取相应雷达辐射源特征,运用各类算法,完成复杂电磁环境下的雷达辐射源识别[8]。 (2)慢三刀、快三刀。相对两虎在中间交叉换位后,四名斗虎英雄在领舞者的指挥下踏鼓点统一分别由内向外对准虎脸上三大步,慢劈三刀将“老虎”逼回原位,紧接相对两虎在斗虎英雄的引领下跑至中间两虎相遇交叉换位。四名斗虎英雄踏鼓点分别由内向外对准虎脸上三大步,快劈三刀将老虎逼回原位,老虎“饿虎扑食”,斗虎英雄带刀就地十八滚从老虎腹下蹿出,向老虎劈出一刀,引领“老虎”向前跃出。 图2 雷达辐射源识别模型 本文采用聚类算法进行辐射源识别,聚类算法就是依据在研究对象中提取的相关信息,按一定准则将对象分组。从相关性的角度来理解就是组内数据之间具有较强的相关性,相关性越强,组内数据聚类性越好,组间差距也就越大;不同组数据间则不相关。为较好说明这个概念,下面给出几条定义[9]: 定义1设有两个特征矢量x=(x1,x2,…,xn)′和y=(y1,y2,…,yn)′,则二者各相应分量之间的差值函数即为距离测度,记为d(x,y),其具体计算如下: (9) 定义2设有集合S={x1,x2,…,xn},其中任意两个元素xi,xj(i,j=1,2,…,n)之间的距离满足下面不等式: dij≤δ (10) 式中δ表示给定阈值,则称集合S对于阈值δ构成一类。 为能够针对实际情况进行讨论,计算所研究对象中的类内距离、类间距离,结合上述两个定义,这里再给出两条准则函数: (11) 式中mj表示第j类的模式均值矢量: (12) 准则2由准则1可得到类间距离函数为 (13) 式中mj表示第j类的模式均值矢量,m为总的模式均值矢量,二者的计算如下: (14) 式中nj为第j类中的模式数[10]。 5.1滤波器设计 为使试验具有普遍性意义,这里假设截获的辐射源脉内为线性调频的脉冲信号,载频为f0=10MHz,线性调频带宽为B=10MHz,采样频率为fs=70MHz,信号脉宽为τ=10μs,脉冲重复周期设为Tr=40μs,并以信噪比SNR=10dB加入高斯白噪声,此时信号的时频特性如图3所示。 图3 线性调频信号的时域波形和频谱 鉴于该信号的频带范围,将巴特沃斯带通滤波器的通带频率设置在8MHz~22MHz,带通和带阻的衰减系数根据经验值分别设为2和12,此时滤波器的阶数为6,其幅频特性如图4所示。 图4 阶巴特沃斯滤波器幅频特性图 为模拟较真实的信号环境,也为便于比较滤波前后的信号变化规律,这里按信噪比SNR=10在信号中加入高斯白噪声,则该信号通过滤波器后的形式如图5所示。 因篇幅有限,也为突出研究的主题,在后续试验中,考虑截获辐射源信号的接收机是同一部,其滤波器对各个辐射源信号的影响相同,并假设信号传播环境理想,对脉冲信号不产生畸变、衰减、散射等,同时忽略多径效应。 图5 线性调频信号通过巴特沃斯带通滤波器 5.2Hilbert法提取脉冲包络 通过滤波得到较纯净的辐射源信号,现利用Hilbert变换法提取信号包络,其思想已在前文进行了阐述,这里直接利用Matlab对信号进行处理: 由图6(b)分析可知,此时得到的信号包络比较参差、抖动性较大,严重影响了后续对信号包络进行参数测量和提取脉冲角度特征的精度,因此,接下来对用Hilbert法提取后的信号包络进行曲线拟合。 图6 Hilbert法提取信号包络 5.3基于三次样条函数的包络曲线拟合 三次样条函数的概念已在前文进行了具体介绍,此处不再赘述,在进行插值处理前,首先找到信号的极值点,如图7所示。 图7 信号极值点 在此基础上,利用三次样条函数的思想,进行插值处理,经曲线拟合后的信号包络形式如图8所示。 图8 三次样条拟合后的包络曲线 对比图6(b)和图8(b)对脉冲包络的局部(脉冲上升沿部分)的放大图可明显看出,经过三次样条曲线拟合后的脉冲信号包络更加连续、平滑,对后续信号处理和数据提取的精度有较大改善。在经过三次样条曲线拟合后的信号包络基础上,依据前文提取脉冲角度特征的方法步骤,便可得到想要的脉冲角度特征值。 5.4基于脉冲角度特征的辐射源识别 为说明脉冲角度特征的聚类性,这里引入一阶差分波形的高阶矩特征,令信号的一阶差分波形为s(t),仍以线性调频信号为例,将信号载频设为20MHz,采样频率设为70MHz,调频信号带宽设为10MHz,脉宽设为16μs,首先利用上文所述提取脉冲包络的方法提取脉冲信号包络,然后根据一阶差分的定义提取脉冲信号包络曲线的一阶差分波形,分别如图9所示。 图9 信号包络的一阶差分波形 对s(t)进行Hilbert变换后得到的式子记为s′(t),则二者合成包络为 ξ(t)=[s2(t)+s′2(t)]1/2 (15) 根据二阶矩、四阶矩的定义,可分别用下面两式求得: m2=E[ξ2(t)],m4=E[ξ4(t)] (16) 结合式(X、X),即可得包络一阶差分波形的高阶矩特征表达式如下[2]: (17) 在此基础上,从三部实际雷达中各提取10组辐射源信号的包络采样值,其中A,B为两种不同型号的雷达,B1,B2为相同型号的两部雷达,均采用相同数据条件的线性调频信号(数值设定同上),分别计算三个辐射源的脉冲角度特征的上升/下降沿角度信息值及包络一阶差分波形的高阶矩特征值,具体测量结果见表1。 表1 三个辐射源的脉冲角度特征及一阶差分高阶矩特征值 根据实际测量值,分别以三者作为x,y,z坐标画图,如图10所示。 图10 三部雷达辐射源信号的聚集性 由图10易见,从不同雷达辐射源信号中提取的脉冲角度特征具有一定的聚类特性,说明该特征参数适用于雷达辐射源精确识别。 由此,从A、B1、B2三类辐射源参数中各再采集200组数据,依据聚类算法中类内距离最小准则进行测试,结果如表2。 表2 辐射源正确识别率 本文根据对脉冲“指纹”特征的学习,重点研究了其中的脉冲包络特征,并对其中的滤波器设计、曲线拟合等关键步骤进行了介绍,在此基础上提出利用脉冲角度特征进行雷达辐射源分类识别的方法,为说明该类特征具有良好的聚类性,引入了脉冲包络的一阶差分波形高阶矩特征,最后通过三组实例,仿真验证了利用本文提取的脉冲角度特征对雷达辐射源进行分类识别,能够得到理想的结果,有益于提高雷达告警正确率。 [1] 潘继飞,姜秋喜,毕大平.雷达_指纹_参数选取[J].现代防御技术,2007,35(1):71-75. [2]林震鹊,姜秋喜,李帅.基于脉冲信号上升_下降沿的雷达辐射源识别[J].舰船电子对抗,2009,32(3):33-37. [3]王宏伟,赵国庆,王玉军.基于脉冲包络前沿高阶矩特征的辐射源个体识别[J].现代雷达,2010,32(10):42-45. [4]王大伟,贾荣丛,王划一.基于Matlab的巴特沃斯滤波器设计[J].现代电子技术,2012,35(21):71-75. [5]张国柱,黄可生,姜文利,等.基于信号包络的辐射源细微特征提取方法[J].系统工程与电子技术,2006,28(6):795-797. [6]钟佑明,金涛,秦树人.希尔伯特_黄变换中的一种新包络线算法[J].数据采集与处理,2005,20(1):13-17. [7]陈文略,王子羊.三次样条插值在工程拟合中的应用[J].华中师范大学学报,2004,38(4):418-422. [8]姚坤.雷达辐射源信号识别技术研究[D].南京:南京信息工程大学,2011. [9]姜园,张朝阳,仇佩亮,等.用于数据挖掘的聚类算法[J].电子与信息学报,2005,27(4):655-662. [10] 孙即祥.现代模式识别[M].长沙:国防科技大学出版社,2002. Radar Emitter Recognition and Implementation Based on Pulse Angle Feature* According to the present problem that the radar warning receiver doesn’t have high precision in emitter recognition, a new kind of fingerprint feature “pulse angle” is proposed. In order to get this character, the signal envelope should be extract with Hilbert method first, then make the envelope curve fitted by cubic spline interpolation function, and the clustering feature of the pulse angle character has been proved. At last, it is verified by the instance simulation that the pulse character can be used to recognize the radar emitter. fingerprint feature, pulse envelope, pulse angle feature, emitter recognition 2016年2月8日, 2016年3月25日 谭龙,男,硕士,研究方向:雷达对抗。 TN95 10.3969/j.issn.1672-9730.2016.08.0243 脉冲角度特征的提取
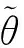
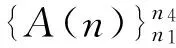
4 基于聚类算法的辐射源识别
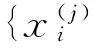
5 仿真验证


6 结语

