基于Entropy-Topsis的水面舰艇防空威胁判断研究*

张　莉

(海军大连舰艇学院　大连　116043)

ZHANG Li

(Dalian Naval Academy, Dalian　116043)



基于Entropy-Topsis的水面舰艇防空威胁判断研究*

张莉

(海军大连舰艇学院大连116043)

首先阐述了水面舰艇防空威胁判断指标选取原则,在此基础上从多个不同角度选取出了反映空中目标威胁的指标,将其归结为一个多属性决策问题,使用Entropy-Topsis模型予以解决。该方法的优点在于威胁排序输出快速可信、易于实现,对于不断变化的空情威胁,可进行持续计算输出。最后,通过仿真示例验证了模型的有效性与可行性。

威胁判断; 防空作战; Entropy-Topsis模型

ZHANG Li

(Dalian Naval Academy, Dalian116043)

Class NumberE917

1　引言

随着反舰导弹和作战飞机性能的不断进步提升,水面舰艇面临的防空压力越来越大,特别是面对多批连续饱和、多平台多方向攻击时,水面舰艇处于劣势更为明显,舰艇指挥员难以做出快速精准对抗决策。因此,在获取来袭空中目标一定数据基础上,借助辅助决策手段,快速、合理对目标进行威胁排序,并在第一时间做出抗击行为,是水面舰艇生存关键所在[1～2]。水面舰艇防空威胁判断,可归结为多属性决策问题。

2　水面舰艇防空威胁判断指标选取

2.1指标选取原则

水面舰艇防空威胁判断指标选取的科学合理,直接影响威胁判断结果输出准确性,在选取威胁判断指标时应遵循以下原则:

1) 选取能够反映目标威胁的关键因素作为指标。如果威胁判断指标选取过多,不仅会导致计算繁琐、降低结果获取时效性,而且还会湮没关键指标价值,降低结果准确性。

2) 要充分利用已分析获取的信息作为指标。威胁判断属于高层信息融合层,在进行威胁判断时要利用已有分析数据,比如目标类型、毁伤能力等,作为参考指标。

3) 选取指标要能够反映目标意图信息[3～4]。比如,目标航路勾径、飞行高度、方位距离、飞行动作、飞行速度等,都一定程度上揭示了目标意图信息。

2.2指标选取[5～6]

根据上述原则,本文选取的威胁判断指标如下:

1) 航路勾径。一般认为,目标航路勾径越小,目标攻击意图越强,威胁也越大。

2) 飞行高度。由于舰载雷达受地球曲率所限和海杂波影响,目标飞行高度越低,不仅不易被探测到,而且压缩了雷达发现距离,造成舰艇拦截时间紧迫,对舰艇威胁越大。

3) 飞行速度。同型目标,飞行速度越高的,被拦截可能越低,突防概率越高,对舰艇造成的威胁越大。

4) 毁伤能力。目标毁伤能力是指,在舰艇不采取对抗条件下,目标对其造成最大毁伤的能力。目标毁伤能力越强,则目标对舰艇威胁程度越大。

5) 目标类型。不同类型目标给水面舰艇带来的威胁亦不相同。

6) 飞抵舰空武器拦截起始线时间。若目标在舰空导弹拦截区外时,飞抵舰空武器拦截起始线时间越快,则舰艇决策时间越短,对舰艇威胁程度越大。

上述指标中,目标飞行高度、速度、航路勾径和飞抵时间不难得到,而目标类型和毁伤能力需要事先判断和计算得出。一般认为,目标毁伤能力由其类型T(j)、装备的反舰武器类别W(k)、相应武器单发命中概率PW(k)、毁伤一艘水面舰艇的平均必须命中弹数ωW(k)、各反舰武器数量NW(k)等因素决定。

有目标毁伤能力βj:

(1)

计算目标毁伤能力关键在于获取目标类型,一旦类型得知,便可根据战场情报和经验数据得出式(1)中T(j)、W(k)、PW(k)、ωW(k)和NW(k)等值。

目标类型可以通过其飞行高度、速度、动作、加速度、回波特征等外在特点进行判别[2],甚至可以通过预先侦查直接获取。本文直接给出的目标类型与其对舰艇威胁系数对应关系,如表1所示。

表1　目标类型及其威胁系数

表1中的掠海快速和不明目标,应根据实际情况对其速度和航路勾径做出具体限值说明,这里不具体给出。无法计算目标毁伤能力,但其威胁系数被归为其它可计算毁伤能力目标的同一类时,其毁伤能力应参考该类其它目标。

3　基于Entropy-Topsis的水面舰艇防空威胁判断[7～8]

2.2节从多个不同角度选取了反映目标威胁情况的指标,可看作为一个待进行威胁判断目标的多个属性。因此,水面舰艇防空威胁判断,可归结为多属性决策问题。

3.1Entropy-Topsis模型介绍

Topsis全称是“逼近与理想值的排序方法”,适用于根据多个指标,对多个方案(目标)进行比较和选择[9],但在确定各指标权重过程中由主观方法直接给出,难以保证方案优选客观性和可信度。因此,在使用Topsis法时必须借助客观赋权法,以确保优选结果的客观准确性。信息论中,熵(Entropy)代表某指标在该问题中提供有效信息量多少的程度,用来度量数据有效信息量,因此熵权可以确定权重[4]。

3.2基于Entropy-Topsis的防空威胁判断模型[10]

基于Entropy-Topsis的防空威胁模型具体计算步骤如下:

1) 设待进行威胁判断的目标为X={x1,x2,…,xm},选取威胁判断指标集为O={o1,o2,…,on},目标xi(i=1,2,…,m)关于指标oj(j=1,2,…,n)的指标值可以表示为yij。所有指标值均可用简记做矩阵形式Y=(yij)m×n,Y为待进行威胁判断的决策矩阵;

2) 对决策矩阵Y元素yij进行极差变换,将其转化为规范化决策矩阵R=(rij)m×n;

当威胁判断指标oj属于效益型指标时:

(2)

效益型指标是指随着指标oj数值增大,目标xi对水面舰艇的威胁度同向加大。显然,2.2节所选取的六个指标中,飞行速度、毁伤能力和类型威胁系数为效益型指标。

当威胁判断指标oj属于成本型指标时:

(3)

成本型指标是指随着指标oj数值增大,目标xi对水面舰艇的威胁度减小。飞抵舰空武器拦截起始线时间、航路勾径和飞行高度为成本型指标。

3) 使用熵权法计算威胁判断指标oj权重方法如下:

(4)

(5)

上式中当fij=0时,lnfij无意义,因此对fij的计算加以修正,将其定义为

(6)

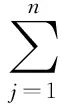
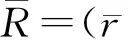
(7)

(8)

与

(9)

式中,Ωb为效益型指标。

6) 计算各待进行威胁排序目标与正负理想解的欧氏距离:

(10)

(11)

7) 计算各待进行威胁排序目标与正负理想解的相对贴近度Ci。

(12)

不难看出,Ci∈[0,1],且Ci值越大,目标xi的威胁越大。

8) 根据所得相对贴近度Ci对选取空中目标进行威胁排序,形成排序序列,为指挥员提供辅助决策结论。

4　仿真示例

4.1仿真数据

设T时刻某驱逐舰对空警戒雷达发现防区外6批空中来袭目标,其中2批判为L型反舰导弹,剩余4批判为携带2枚L型反舰导弹和1枚M型制导炸弹的K型歼轰机。根据经验数据和情报信息得出L型和M型武器的相关数据如表2所示。

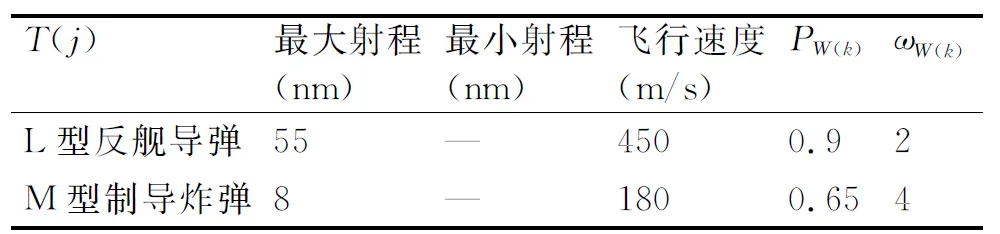
表2　L型和M型武器的相关数据

通过式(1)可计算得出L型反舰导弹和K型歼轰机的毁伤能力量化分别为0.45和0.7467。根据雷达获取数据,得到六批目标威胁判断初始数据如表3所示。

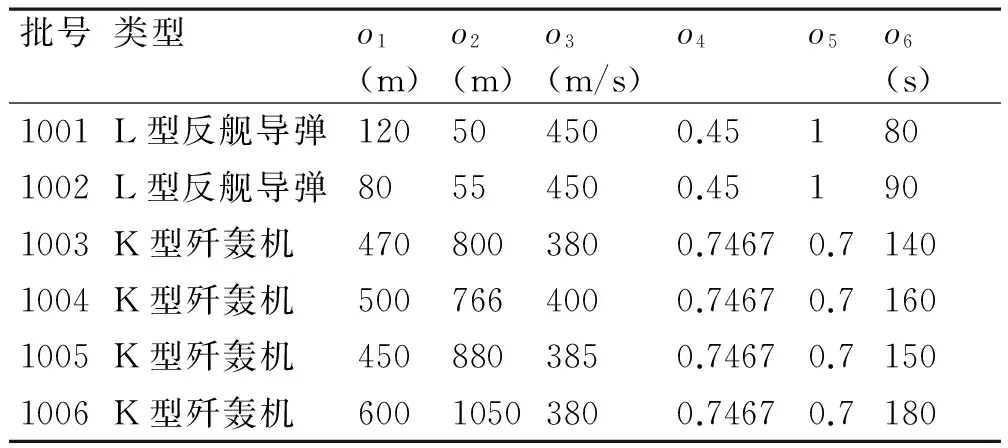
表3　来袭目标威胁判断初始数据

表3中,指标o1、o2、o3、o4、o5和o6分别为航路勾径、飞行高度、飞行速度、毁伤能力系数、目标类型威胁系数和飞抵某驱逐舰舰空武器拦截起始线时间。

4.2仿真结果

应用Entropy-Topsis模型对上述六批目标进行威胁判断计算过程如下:

1) 根据表3数据,得到水面舰艇防空威胁判断问题的决策矩阵Y:

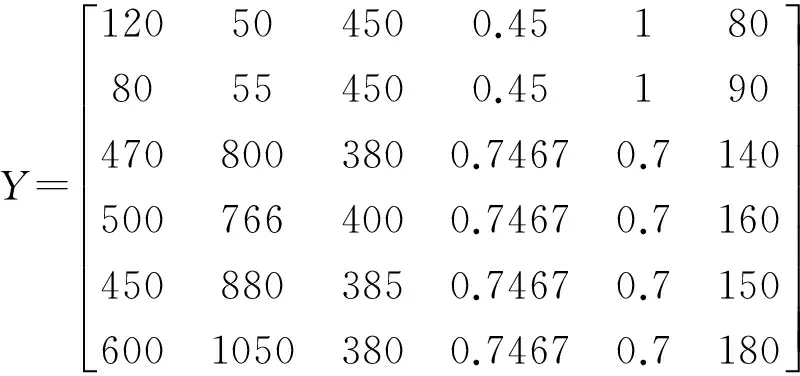
2) 利用式(2)、式(3)对矩阵Y元素yij进行极差变换,可得规范化决策矩阵R:

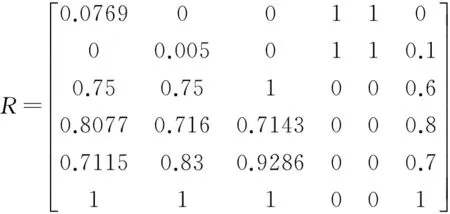
3) 利用式(4)、式(5)和式(6)可计算出指标o1到o6的权重分别为:0.1760、0.1770、0.1947、0.1483、0.1483、0.1557。

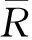
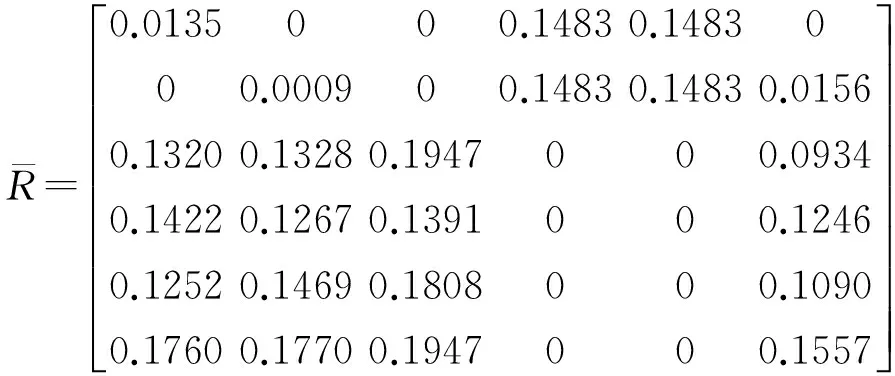
r+=(0.1760,0.1770,0.1947,0.1483,0.1483,0.1557)

和

r-=(0.0000,0.0000,0.0000,0.0000,0.0000,0.0000)

6) 利用式(10)、式(11)和式(12)分别计算各目标与正负理想解的欧式距离和相对贴近度Ci。

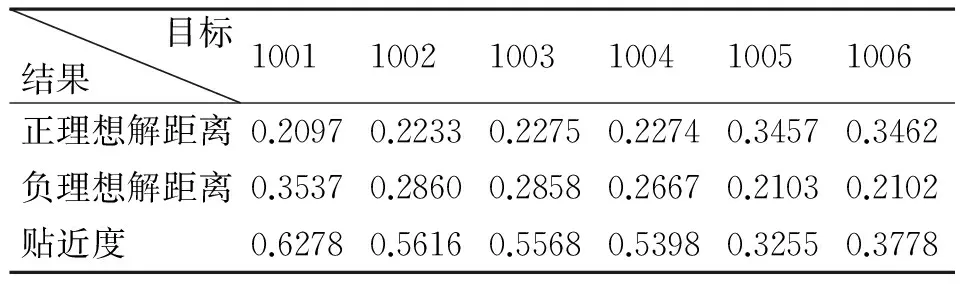
表4　各目标与正负理想解的欧式距离及贴近度

从表4计算结果可以看出,导弹较飞机对舰艇威胁较大,T时刻1001批L型反舰导弹对某驱逐舰威胁最大,1002、1003、1004、1006和1005依次次之,计算结果符合定性分析和一般认知。

5　结语

水面舰艇在防空作战时,对目标威胁判断的合理与否将直接影响后续抗击决策的科学性,在做出合理判断基础上,越快给出判断结论,则留给后续抗击时间越充裕,防空作战效益也会随之提升。本文给出的水面舰艇威胁判断模型,指标数据信息较易获取、计算过程简单可行、易于工程实现、威胁排序输出快速可信,对于不断变化的空情威胁,可进行持续计算输出,是一种行之有效的水面舰艇防空威胁判断辅助决策方法,具有一定的参考借鉴价值。

[1] 王永春,缪旭东,王义涛.直觉模糊条件下舰艇编队防空威胁估计决策模型[C]//系统仿真技术及其应用学术年会论文集——系统仿真技术及其应用第十卷,2008,7:186-189.

[2] 张磊,童幼堂,徐奕航.舰艇编队空中目标威胁排序模型研究[J].舰船电子工程,2009,29(6):136-138.

[3] X. T. Nguyen. Threat Assessment in Tactical Airborne Environments[C]//ISIF,2002:1300-1307.

[4] Alessio Benavoli, Branko Ristic. An Approach to Threat Assessment Based on Evidential Network[C]//10th International Conference on Information Fusion,2007:1235-1242.

[5] 符永军,方棉佳,张永顺.模糊多因素多层次评判在目标威胁度中的应用[J].火力与指挥控制,2004,29(3):88-90.

[6] 潘科,潘宣宏,郭新奇.基于多属性决策的护航舰艇防空威胁判断分析[J].计算机与数字工程,2014,42(5):802-805,821.

[7] 王风雷,孙莹.基于熵值TOPSIS法的旅游上市公司绩效评价[J].商丘职业技术学院学报,2012,11(3):42-44.

[8] 吴金平,陆铭华,黄文斌,等.水面舰艇编队对反舰导弹的威胁判断研究[J].系统仿真学报,2004,16(5):879-882.

[9] 张宇,王义涛,孙庆声.基于Entropy-Topsis的水面舰艇编队防空配置方案优选[J].指挥控制与仿真,2015,37(2):31-35,47.

[10] 王光源,马海洋,庞文强.基于熵与TOPSIS法的空中目标威胁判断[J].海军航空工程学院学报,2011,26(2):233-237.

Target Threat Assessment in Surface Antiaircraft Based on Entropy-Topsis*

Firstly this paper elaborates the principle of index selection about the warship air defense threat judgment, on the basis on this the indexes reflecting the aerial targets threat are selected from many different angles, and the warship air defense threat judgment can be attributed to a multi-attribute decision problem which can be solved by using the Entropy TOPSIS model. The advantage of the method is that the output of the threat sequencing is rapid, reliable and easy to realize. It can also calculate the output continuously about the constantly changing aerial threats. At last, the validity and feasibility of the model are verified by simulation examples.

threat assessment, anti-air warfare, Entropy-Topsis model

2015年2月7日,

2015年3月20日

张莉,女,博士,研究方向:模拟训练及仿真。

E917

10.3969/j.issn.1672-9730.2016.08.014