光滑分段孪生支持向量机*

吴　青， 王彦彦， 薛　飞

(1.西安邮电大学 自动化学院，陕西 西安 710061；2.西安邮电大学 通信与信息工程学院，陕西 西安 710061)



光滑分段孪生支持向量机*

吴青1， 王彦彦2， 薛飞2

(1.西安邮电大学 自动化学院，陕西 西安 710061；2.西安邮电大学 通信与信息工程学院，陕西 西安 710061)

为了解决Sigmoid的积分函数对正号函数的逼近精度低的问题，引入一种具有更强逼近正号函数能力的光滑函数即分段函数，提出了光滑分段孪生支持向量机，并用快速Newton-Armijo算法对其求解。在NDC和UCI数据集上的实验结果表明：光滑分段孪生支持向量机能够有效地处理大规模和高维度数据，且分类精度和分类速度与光滑孪生支持向量机相比得到了改进。

光滑孪生支持向量机； 光滑分段函数； Newton-Armijo算法

0　引　言

孪生支持向量机(twin suppor vector machine,TWSVM)[1]是2007年在广义特征近似支持向量机(GEPSVM)[2]思想基础上提出来的。如果只考虑二类问题，TWSVM目的是要寻找两个非平行超平面。这两个超平面能够很好地把两类样本分开，其中一类样本要尽可能在本类超平面的周围，同时要尽可能远离他类的超平面。标准支持向量机(SVM[3])解决一个较大二凸次规划问题(QPPs)，其约束条件是为了让两类样本尽可能分布在超平面的两侧。而TWSVM解决两个较小的QPPs，每一个QPPs在形式上与标准SVM相似,但相对应的约束条件却是为了保证他类样本尽可能远离本类超平面。TWSVM现已被应用到说话人识别[4]、医学检测[5,6]等领域。但是由于TWSVM的目标函数中存在不光滑项，只能在对偶空间上求解两个小QPPs。这种求解方法对于样本数目较大的问题将受到时间和内存的制约。2008年,Kumar M A等人引入正号函数并利用Sigmoid的积分函数作为光滑函数逼近正号函数，提出了光滑TWSVM(STWSVM)[7,8]。但是由Sigmoid的积分函数对正号函数的逼近精度低导致了分类精度不太理想。

本文引入分段函数[9]对TWSVM中的不光滑项逼近，提出了光滑分段孪生支持向量机模型(SPTWSVM)。理论上证明了SPTWSVM具有严凸性、二阶光滑和全局收敛的性能。最后使用快速牛顿Armijo[10,11]算法优化其模型。

1　分段光滑函数

本文采用的分段光滑函数φ(x,k)来逼近正号函数x+，φ(x,k)的形式为

(1)

式中光滑参数k>0。

性质1已知光滑分段函数函数φ(x,k)和正号函数x+，则有

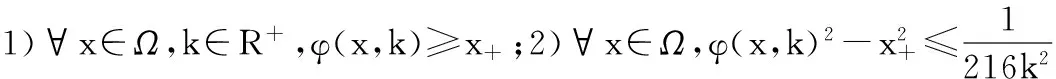
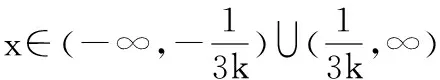
2　光滑分段孪生支持向量机模型

用光滑分段函数来逼近正号函数得到光滑分段孪生支持向量机的模型为

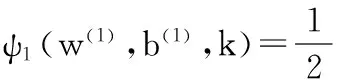
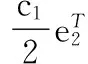
(2)

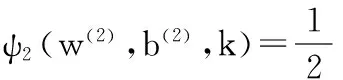
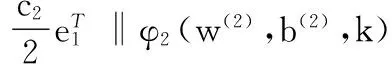
(3)

式中矩阵A和矩阵B分别为+1类和-1类样本。φ1(w(1),b(1),k)和φ2(w(2),b(2),k)是分段函数。

定理1对任意的w(1)∈Rn，w(2)∈Rn，b(1)∈Rn，b(2)∈R，k>0，ψ1(w(1),b(1),k)和ψ2(w(2),n(2),k)是连续可微且严格凸的。

证明：由性质1可知ψ1(w(1),b(1),k)是连续且可微的。由于‖·‖2是严格凸函数。所以定理1得证。

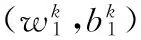
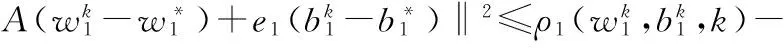
3　实验与分析

为了验证SPTWSVM能够有效地处理大规模高维的数据，表1和表2分别从线性和非线性两种情况在NDC数据集[12]上进行实验。本文设定SPTWSVM ,STWSVM的线性情况下的惩罚参数c1=c2=1，非线性情况下惩罚参数c1=c2=100，高斯核函数的参数δ=0.25。由表1和表2可以看出：当训练样本达到100 000时，TWSVM算法由于运行时间过长已经失效了。然而SPTWSVM可以在较短的时间内得到较高的分类正确率。

表中的‘k’表示1 000个样本。‘-’表示时间过长，结果无效。为了进一步证明SPTWSVM的分类性能。又将TWSVM,STWSVM，SPTWSVM在UCI数据库上进行实验。表3和表4分别是线性情况和非线性情况下的实验结果，其中，线性情况下的惩罚参数c1=c2=1，非线性情况下惩罚参数c1=c2=100，高斯核函数的参数δ=0.25。表3和表4的结果表明，SPTWSVM可以在较短的时间内达到较高的分类精度。

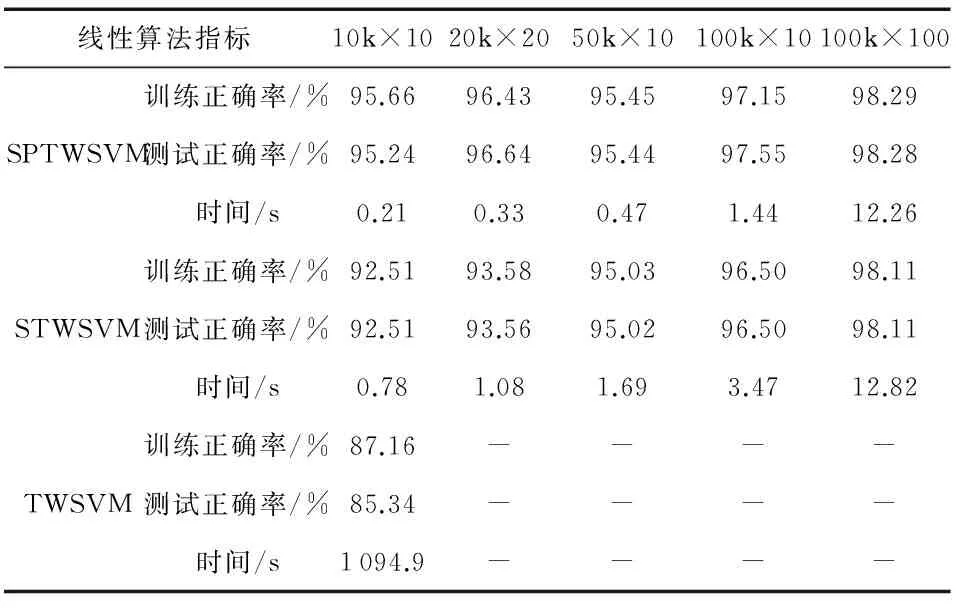
表1　线性算法对NDC数据集的测试结果

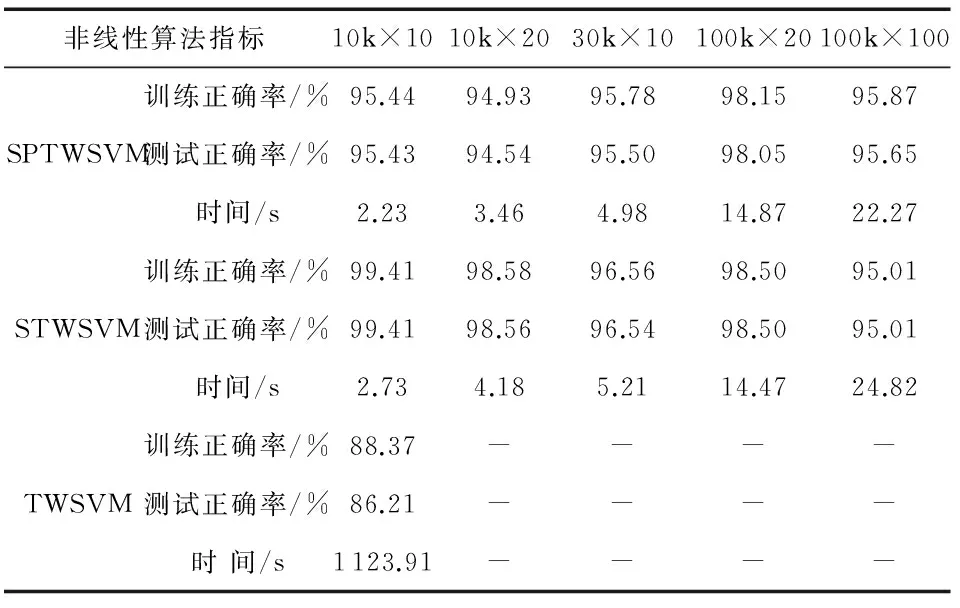
表2　非线性算法对NDC数据集的测试结果

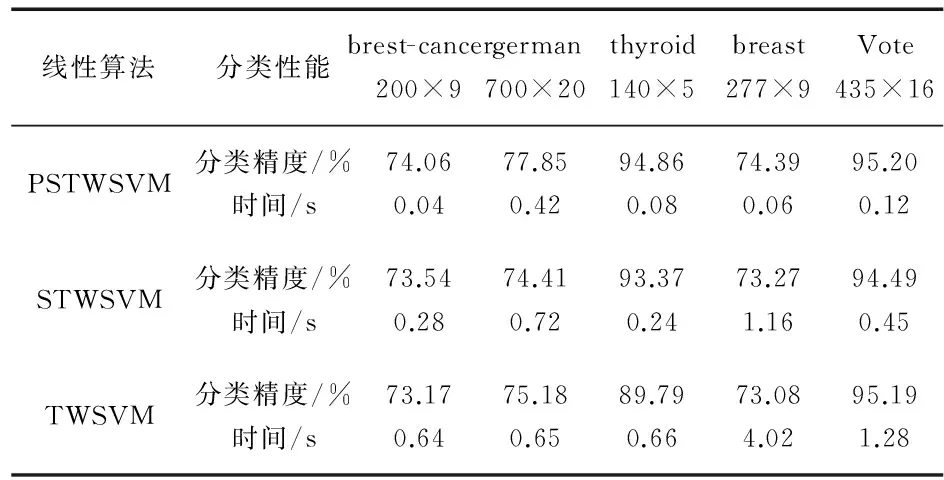
表3　线性算法对UCI数据集的实验结果

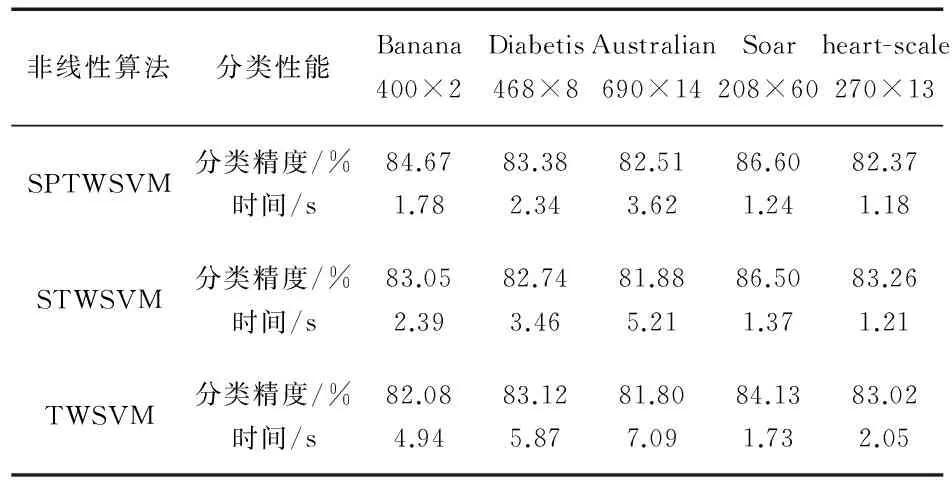
表4　非线性算法对UCI数据集的实验结果

4　结　论

本文引入分段函数逼近孪生光滑支持向量机模型中的不可微项，提出了光滑分段孪生支持向量机，并用快速Newton-Armijo算法求解SPTWSVM模型。SPTWSVM与STWSVM相比，在分类精度和时间上都有所提高。但是两者都没有考虑到噪声和野点对其分类超平面的影响，仍然有错分的情况存在。所以，接下来的工作就是在把光滑技术应用到TWSVM的同时考虑模糊技术是不是也可以应用到其中。

[1]Jayadeva Khemchandni R,Chandra S.Twin support vector machines for pattern classification[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2007,29(5):905-910.

[2]Mangasarian O L.Wild E W.Multi-surface proximal support vector machine classification via generalized eigenvalues[J].IEEE Trans on Pattern Analysis and Machine Intelligence,2006,28(1):69-74.

[3]Vapnik V.The nature of statistical learning theory[M].New York:Springer,2000.

[4]Cong Hanhan,Yang Chengfu,Pu Xiaorong.Efficient speaker recognition based on multi-class twin support vector machines and GMMs[C]∥IEEE Conference on Robotics,Automation and Mechatronics,2008:348-352.

[5]Zhang Xinsheng,Gao Xiaobo,Wang Ying.Twin support tensor machine for MCS detection[J].Journal of Electronics,2009,26(3):318-325.

[6]Zhang Xinsheng,Gao Xiaobo.MCS detection approach using bagging and boosting based twin support vectoe machine[C]∥Proc of the 2009 IEEE Int’l Conf on System,Man,and Cybernetics,Piscataway:IEEE,2009:5000-5005.

[7]Lee Y J,Mangasarian O L.SSVM:A smooth support vector machine for classification[J].Computationl Optimization and Application,2001,22(1):5-21.

[8]Kumar M A,Gopal M.Application of smoothing technique on twin support vector machines[J].Pattern Recognition Letters,2008,29(13):1842-1848.

[9]Wu Qing.Piecewise-smooth support vector machine for classification [J].Mathematical Problems in Engineering,2013(3):2-9.

[10] 李广明，刘群锋．光滑支持向量机两种求解算法的比较[J]．计算机应用，2009，29(6)：1612-1614.

[11] 吴青，赵雄.一类新样条光滑支持向量机[J].西安邮电大学，2013，18(6)：68-74.

[12] Huang Hanpang,Liu Yihung.Fuzzy support vector machines for pattern recognition and data mining[J].Int’Journal of Fuzzy Systems,2002,4(3):826-835.

Smooth piecewise twin support vector machine*

WU Qing1, WANG Yan-yan2, XUE Fei2

(1.School of Automation,Xi’an University of Posts and Telecommunications,Xi’an 710061,China; 2.School of Communication and Information Engineering,Xi’an University of Posts and Telecommunications,Xi’an 710061, China)

To solve the problem of low approximation precision of integral function of sigmoid function,a piecewise function is introduced,which has stronger ability of smooth function of smooth piecewise function to approximate plus function. Smooth piecewise twin support vector machine(SVM)is proposed.Meanwhile,the fast Newton-Armijo algorithm is used to solved the smooth piecewise twin SVM.Experimental results on NDC and UCI datasets show that smooth piecewise twin SVM can effectively deal with large-scale and high-dimensional data,and classification precision and classification speed of smooth piecewise twin SVM are improved than smooth twin SVM.

smooth twin support vector machine(STWSVM); smooth piecewise function; Newton-Armijo algorithm

10.13873/J.1000—9787(2016)09—0130—03

2015—11—24

国家自然科学基金资助项目(61100165);陕西省自然科学基金资助项目(2014JM8313);陕西省教育厅科学研究计划资助项目(2013JK1023)

TP 18

A

1000—9787(2016)09—0130—03

吴青(1975-)，女，山东临沂人，博士，副教授，从事机器学习研究。