改进的IMU传感器安装误差正交补偿方法*

马亚平, 魏　国, 周庆东

(哈尔滨工业大学 自动化测试与控制系，黑龙江 哈尔滨 150001)



改进的IMU传感器安装误差正交补偿方法*

马亚平, 魏国, 周庆东

(哈尔滨工业大学 自动化测试与控制系，黑龙江 哈尔滨 150001)

针对传统的正交补偿方法难以保证惯性测量单元具有较高的正交补偿精度的问题，提出了一种改进的适用于大角度和小角度安装误差角情形的正交补偿方法，该方法分别建立三轴加速度计和三轴光纤陀螺传感器的安装误差方程，对惯性测量单元进行速率标定和多位置静态标定，并利用最小二乘法求解惯性测量单元的安装误差方程参数。仿真和实验结果表明：该方法较传统的正交补偿方法具有较高的正交补偿精度和传感器标定精度，且回避了静态标定时在较大安装误差角下利用转位机构获得零偏存在较大误差的问题，大大地提高了标定效率。

惯性测量单元； 大角度安装误差； 正交补偿； 最小二乘法

0　引　言

捷联惯性系统是将加速度计和陀螺仪组成的惯性测量单元(inertial measurement unit,IMU)直接固连在运载体上(如测斜仪、舰艇和飞机等)，根据惯性传感器IMU提供的测量值来解算出运载体的姿态信息[1,2]。由于IMU本身存在机械加工工艺和安装结构的限制，不可避免地带来IMU传感器之间以及传感器与安装固件之间的非正交误差，这些误差统一称为IMU安装误差。针对捷联惯性导航系统要求精度较高的情况，需要具有较高的安装误差补偿计算精度[3]。

IMU的标定和安装误差补偿是针对IMU传感器建立相应的数学模型，并进行该数学模型参数计算的过程。在捷联惯性导航系统的标定过程中，实际IMU传感器坐标系与理想载体坐标系之间存在的安装误差不可忽略。在传统的IMU传感器正交补偿中，所采用的补偿方法仅仅适用于较小正交误差(通常小于60″)，并且使用的正交补偿矩阵对角线元素往往近似为单位1[4,5]。但是，当IMU传感器所在的实际坐标系(传感器坐标系)和理想载体坐标系之间存在较大的安装误差角时，采用传统的正交补偿矩阵对对角线元素进行近似处理方法，不能很好地满足系统的标定精度和正交补偿精度的要求。当IMU传感器存在较大的安装误差角时，利用转位机构得到对称位置来计算IMU传感器零偏的误差较大[5～9]。本文提出了一种改进的正交补偿方法，具有较高的惯性传感器标定精度和安装误差补偿精度。

1　惯性测量单元的正交安装误差数学模型

1.1惯性测量单元的正交安装误差

三轴光纤陀螺和三轴加速度计固连在测量短节的骨架上，由于实际系统中机械加工工艺和装配工艺的限制、及惯性测量单元的安装骨架结构的不同，将带来不同大小的安装误差[7,8]。尤其当安装骨架采用圆柱体结构替代通常的长方体结构时，可能会带来径向平面内的基准坐标轴与传感器坐标轴之间存在较大的安装误差角。图1给出了IMU安装在骨架上的结构示意图。

图1　IMU安装在骨架上的结构示意图

如图1所示，小长方体表示加速度计，小圆环表示光纤陀螺仪。图2和图3所示，分别给出了三轴光纤陀螺和三轴加速度计的安装误差示意图。

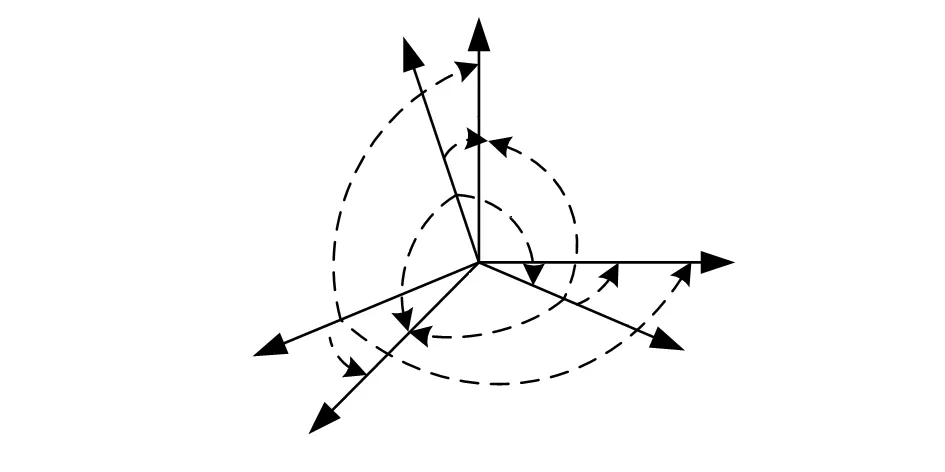
图2　三轴光纤陀螺的安装误差示意图

说明，Oxgygzg表示三轴光纤陀螺传感器坐标系,Oxayaza表示三轴加速度计传感器坐标系。αij表示光纤陀螺传感器坐标系i轴与载体坐标系Oxbybzb的j轴的夹角，即为光纤陀螺传感器安装误差角。βij表示加速度计传感器坐标系i轴与载体坐标系Oxbybzb的j轴的夹角，即为加速度计传感器的安装误差角，αij∈[0°,180°],βij∈[0°,180°]。定义Egij对应αij的余弦值，表示三轴光纤陀螺的正交安装系数，同样也定义。Eaij对应βij的余弦值，表示三轴加速度计的正交安装系数，则存在如下约束关系式(1)和式(2)

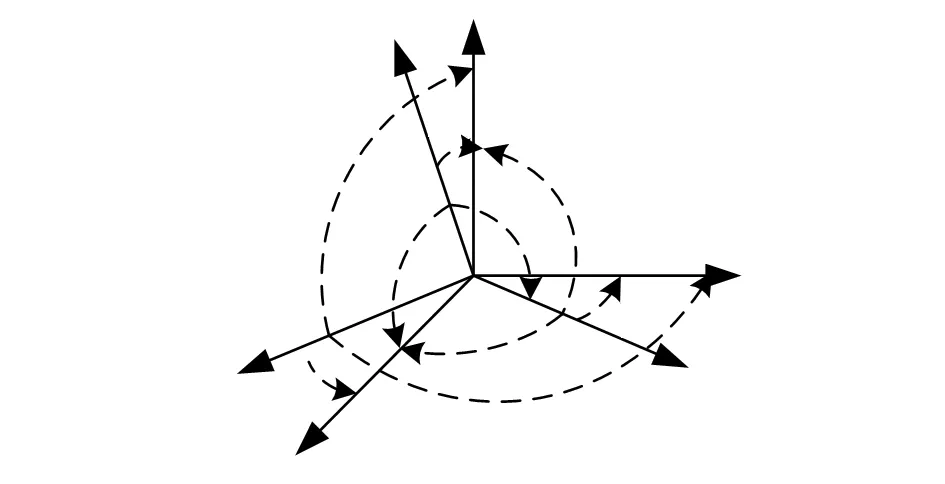
图3　三轴加速度计的安装误差示意图

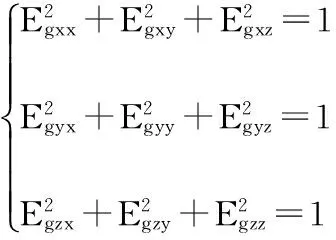
(1)

(2)

由式(1)和式(2)可知，采用新的正交补偿算法进行补偿，大大地降低了系统的加工和安装工艺要求[5～8]。

1.2三轴光纤陀螺的数学模型

惯性测量单元中的三轴光纤陀螺安装在测量短节上，光纤陀螺所在的传感器坐标系和载体坐标系不可避免地存在光纤陀螺组件的非完全正交误差[5]。建立三轴光纤陀螺的安装误差数学模型为

(3)

式中fgx,fgy,fgz分别为三轴光纤陀螺的输出；kgx,kgy,kgz分别为三轴光纤陀螺的标度因数；ωx,ωy,ωz分别为载体坐标系的三轴的速率敏感量；bgx0,bgy0,bgz0分别三轴光纤陀螺的零偏。传统的近似正交补偿方法中，Egxx≈1,Egyy≈1,Egzz≈1，当存在大角度的安装误差角时，不能进行以上的近似处理。

1.3三轴加速度计的数学模型

加速度计数学模型中的交叉耦合项和二阶非线性系数为微小量[7,10]。在对其进行正交标定时，往往忽略交叉耦合项、二阶及以上阶数的非线性系数的影响，仅考虑加速度计的标度因数、零偏和正交安装误差系数，则加速度计的数学模型简化为

Aa=kaai+ba0

(4)

式中Aa为实际输出，ka为标度因数，ba0为零偏，ai为输入加速度。三轴加速度计安装存在非完全正交误差，可建立三轴加速度计的数学模型为

(5)

同样地，在传统的IMU正交补偿模型中，Eaxx≈1,Eayy≈1,Eazz≈1。当存在大角度的安装误差角时，不能进行以上的近似处理。

2　惯性测量单元的正交误差数学模型计算

光纤陀螺的标定需要在高精度三轴转台进行，并且要求状态具有标准的转动速率、姿态、位置信息。通过速率标定来计算光纤陀螺组件的标度因数和安装误差系数。速率标定的旋转示意图如图4所示[8,10,11]。

图4　速率标定示意图

首先，进行图4中的位置a的转台转动。将实际的随钻井斜测量系统骨架固定在转台的内框架上。假设转台坐标系为标准的东北天坐标系，且初始位置和载体坐标系完全重合。将x轴指向天向，然后转台绕天向以角速率ω正向旋转。

光纤陀螺在一个圆周内旋转时进行N次采样，由于sinωt和cosω在一个圆周内积分为零，则

(6)

(7)

式中fgx1+,fgy1+,fgz1+分别为位置a正方向转动光纤陀螺的实际输出。fgx1-,fgy1-,fgz1-分别为位置a负方向转动光纤陀螺的实际输出。

将式(6)和式(7)作差，可得

(8)

同样地，对图4中的位置b和位置c分别进行速率标定，并得到

(9)

式中fgx2+,fgy2+,fgz2+分别为位置b正向转动光纤陀螺的实际输出；fgx2-,fgy2-,fgz2-分别为位置b负向转动光纤陀螺的实际输出

(10)

式中fgx3+,fgy3+,fgz3+分别为位置c正向转动光纤陀螺的实际输出；fgx3-,fgy3-,fgz3-分别为位置c负向转动光纤陀螺的实际输出。进而利用最小二乘法可得Egxxkgx,Egyxkgy,Egzxkgz,Egxykgx,Egyykgy,Egzykgz,Egxzkgx,Egyzkgy和Egzzkgz等9个乘积项。利用约束关系式(1)，分别获得三轴光纤陀螺的标度因数kgx,kgy和kgz，以及其正交安装误差系数Egxx,Egxy,Egxz,kgyx,Egyy,Egyz,Egzx,Egzy和Egzz。本文采用24位置静态标定技术，如图5所示。

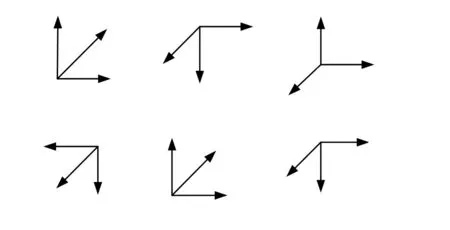
图5　静态24位置标定示意图

(11)

式中Bg0为以[bgx0,bgy0,bgz0]T为列向量组成的维数为3×24的矩阵。式(11)表示的矩阵方程[9,11]，利用最小二乘法得光纤陀螺的零偏分别为bgx0,bgy0和bgz0。

(12)

记式(12)右端前部分的3×4 矩阵为M，同时通过24位置转动获得的输入加速度计矢量矩阵为W，其维数为 4×24，加速度计的输出矩阵为Aa，其维数为4×24。将式(12)扩展为24个矩阵方程，可得含有正交误差系数的矩阵方程为

Aa=M×W

(13)

利用最小二乘法求解加速度计正交补偿矩阵方程的参数，则

M=Aa·WT·(W·WT)-1

(14)

利用式(2)的约束关系和式(14)可得零偏分别为bax0,bay0和baz0，标度因数分别为kax,kay和kaz，三轴加速度计的正交安装误差系数因数分别为 Eaxx,Eaxy,Eaxz,Eayx,Eayy,Eayz,Eazx,Eazy和Eazz。本研究通过任意给定的多位置进行静态标定，回避了需要通过转位机构方法获得对称位置来求解惯性传感器的零偏问题[9]。

3　改进的正交补偿算法仿真与实验

3.1改进的正交补偿算法仿真

假定三轴光纤陀螺和三轴加速度计在同一传感器坐标系，与载体坐标系之间的安装误差系数一致。取地球自转角速率为7.291 6×10-5rad/s，当地的地理纬度为45°，当地重力加速度为9.84 m/s2。倾斜角从-85°～+85°以5°等间隔变化，方位角从10°～350°以10°等间隔变化，工具面角从-170°～+170°以10°等间隔变化。进行正交补偿前后仿真对比分析。充分考虑了在圆柱体径向平面内可能存在较大误差角的情况，给出了IMU安装误差角，如表1所示。

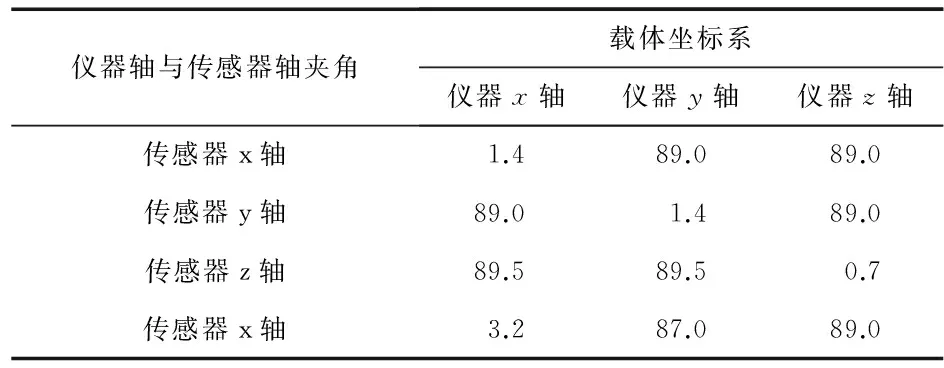
表1　IMU安装误差角/(°)

通过仿真得到，正交补偿前、近似正交补偿后和改进正交补偿后的姿态角误差曲线，分别如图6。由图6可知，利用改进的正交补偿方法获得姿态角误差理论上达到10-13量级水平，该方法具有良好的正交补偿效果。

仿真结果表明，近似正交补偿后的姿态角误差限制在很小的误差范围内，但是仍然存在很大的姿态误差角，很难满足高精度导航系统的要求。而本文改进的正交补偿方法较传统的近似正交补偿可大大缩小姿态角误差范围，提高姿态角精度。

3.2改进的正交补偿算法实验

将装配有IMU的圆柱体测量短节安装在高精度三轴转台上，进行光纤陀螺的速率标定和IMU的24位置静态标定，采用相应的姿态解算方法获得近似正交补偿和提出的正交补偿后的姿态角，如表2和表3所示。其中，θ表示倾斜角，ψ表示方位角，φ表示工具面角，其单位均为角度(°)。

由表2可知，通过近似正交补偿获得的姿态角误差，倾斜角绝对误差可能大于0.15°，方位角绝对误差可能大于1.50°，工具面角绝对误差可能大于0.20°。由表3可知通过改进的正交补偿方法获得姿态角误差均在较小的误差带范围内，大大地提高了姿态角解算精度。另外，改进的正交补偿方法和近似正交补偿计算方法的计算量基本相同。

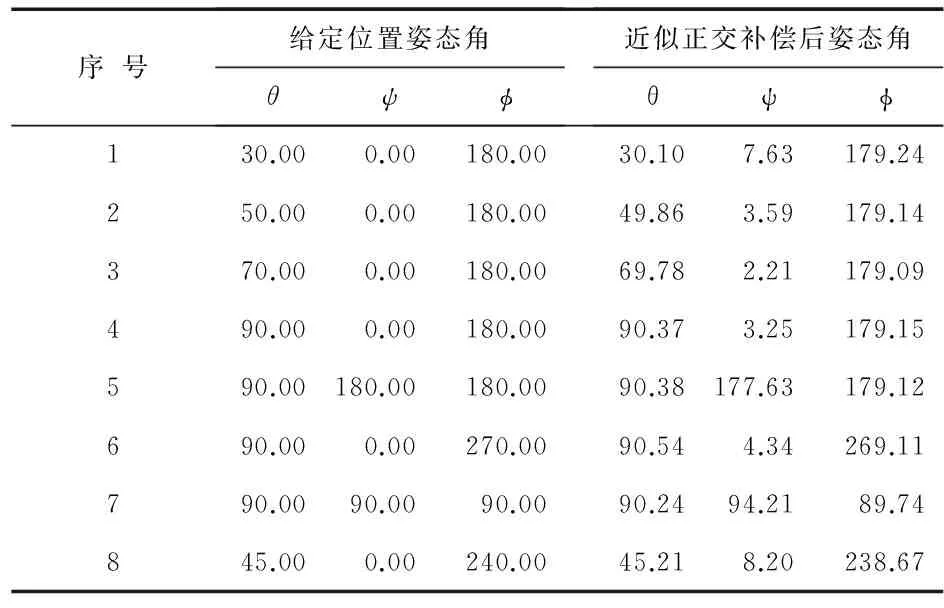
表2　近似正交补偿后的姿态角结果/(°)

图6　正交补偿前后姿态角误差曲线

序号给定位置姿态角θψϕ 改进的正交补偿后姿态角θψϕ130.000.00180.0029.950.20179.73250.000.00180.0049.950.38179.56370.000.00180.0069.930.28179.76490.000.00180.0089.990.34180.01590.00180.00180.0090.01179.75179.98690.000.00270.0089.990.59269.99790.0090.0090.0089.9789.7989.97845.000.00240.0045.050.48239.91

4　结　论

本文针对在捷联惯性导航系统中惯性测量单元可能存在较大安装误差角的问题，提出一种改进的惯性测量单元正交补偿方法。主要针对大角度安装误差情形，给出惯性测量单元安装误差角的约束关系式，建立了三轴光纤陀螺和三轴加速度计的数学模型，并重点推导出相应的改进的正交补偿方法。仿真和实物实验均表明:改进的正交补偿方法具有更高的正交补偿精度，大大地提高了存在大角度安装误差角下的惯性测量单元的速率标定和静态标定的精度，同样也适用于具有小安装误差角的IMU传感器正交补偿的场合。新正交补偿方法，可以通过给定任意多位置进行静态标定，避免了传统方法中使用对称位置法求解惯性传感器零偏的问题，大大提高了IMU静态标定效率。

[1]程世超,高爽,林铁,等.随钻测量用微小型惯性测量单元设计[J].传感器与微系统,2015,34(4):95-98.

[2]高爽,焦禹舜,林铁,等.轻小型二位置光纤陀螺测斜仪惯性测量单元设计[J].传感器与微系统,2014,33(6):86-89.

[3]Bekkeng J K.Calibration of a novel MEMS inertial referenceunit[J].IEEE Transactions on Instrumentation and Measurement,2009,58(6):1967-1974.

[4]李杰,洪惠惠,张文栋.MEMS微惯性测量组合标定技术研究[J].传感技术学报,2008,21(7):1169-1173.

[5]彭孝东,陈瑜,李继宇,等.MEMS三轴数字陀螺仪标定方法研究[J].传感器与微系统,2013,32(6):63-65.

[6]颜苗,翁海娜,谢英.系统参数标定以及惯性元件安装误差测量与补偿技术研究[J].中国惯性技术学报,2006,14(1):27-30.

[7]杨长松,徐晓苏.捷联惯导系统加速度计标度因数和安装误差的试验标定[J].测控技术,2005,24(12):57-59.

[8]张华强,赵剡,陈雨.捷联惯性导航系统整体标定新方法[J].北京航空航天大学学报,2012,5(4):459-463.

[9]高钟毓.惯性导航系统初始对准与标定最优化方法[J].中国惯性技术学报,2009,17(1):1-7.

[10] 郭振芹,段尚枢.石英电容伺服加速度计[J].哈尔滨工业大学学报,1985,1(6):58-64.

[11] Syed Z F,Aggarwal P,Goodall C.A new multi-position calibration method for MEMS inertial navigation systems[J].Measurement Science and Technology,2007,18(7):1897-1907.

魏国，通讯作者，E—mail：wg_weiguo@yahoo.com.cn。

An improved method of orthogonal compensation for IMU installation error*

MA Ya-ping， WEI Guo， ZHOU Qing-dong

(Department of Automatic Testing and Control,Harbin Institute of Technology,Harbin 150001,China)

An improved approach for orthogonal compensation is proposed to solve the problem of traditional method that has difficulty in satisfying relatively higher orthogonal compensation precision of inertial measurement unit(IMU).The installation error equations of both three axis accelerometers and three axis fiber-optic gyro sensors are formulated,respectively.Then rate calibration and multi-position static calibration of IMU are conducted,compute installation error equation parameters of IMU by means of least square algorithm.Both simulated and experimental results show that the proposed orthogonal compensation approach has higher precision in terms of both orthogonal compensation and sensor calibration,as compared with the conventional orthogonal compensation one.Furthermore,the proposed method also solves the problem of calculating the IMU zero bias by using indexing mechanism during static calibration,and thus the calibration efficiency of IMU can be greatly improved.

inertial measurement unit(IMU)； large angle installation error； orthogonal compensation； least square method

10.13873/J.1000—9787(2016)09—0009—05

2016—06—30

中国航天集团哈尔滨工业大学联合技术创新中心项目(CASC—HIT09—2B02)

TE 927

A

1000—9787(2016)09—0009—05

马亚平(1986-)，男，河南虞城人，博士研究生，从事组合惯性导航研究。