工业机器人工作过程中能耗最小控制策略*

操鹏飞,许德章,汪步云,张家敏,杨伟超



工业机器人工作过程中能耗最小控制策略*

操鹏飞1,2,许德章1,2,汪步云1,2,张家敏1,2,杨伟超1,2

(1.安徽工程大学 机械与汽车工程学院,安徽 芜湖241000；2.安普机器人产业技术研究院有限公司，安徽 芜湖241007)

针对工业机器人作业过程中能耗高的问题，提出了一种工业机器人的能耗最小控制策略，有效降低六自由度串联工业机器人在指定轨迹下匀速工作过程中的能耗。在工业机器人腰部、大臂、小臂进行动力学建模基础上，针对机器人的腰关节、肩关节、肘关节等能耗较大关节的驱动电机建立其能耗模型。通过动力学模型和能耗模型推导出机器人目标能量函数，根据约束条件提出了机器人能耗最小控制策略。通过测量机器人各个关节不同转动速度时的电机的输入功率，理论能耗与实验的对比，验证了控制策略的有效性。该控制策略可以有效降低工业机器人的作业能耗，节能增效，并对工业机器人具有普适性。

工业机器人；动力学建模；能耗建模；能耗最小控制策略

0　引言

随着机器人技术的进步，工业化水平的提升和我国人口红利逐渐消退，工业机器人在各行各业得到了广泛应用。然而与行车等起吊设备相比，工业机器人在作业过程中需要更多的电能，如何有效地使用有限的能量同时不降低机器人工业效率变得至关重要。

综合国内外的研究，机器人步态和路径规划等方面针对能耗问题开展了大量研究工作[1-4]，而在工业机器人工作过程中，其运动速度亦影响其能耗，目前国内逐步进行一些在对机器人伺服电机速度控制方面的能耗问题的研究。文献[5-6]得出能耗公式，用于比较不能的评价方法，没有针对某一因素进行研究。文献[7]针对两轮自平衡机器人建立了能耗函数并求解，得出最小能耗时的速度大小，从而提出了优化策略，而工业机器人运动复杂，变量多，两轮自平衡机器人的优化策略并不适用。文献[8]提出了多关节机器人的能耗优化策略，但其规划的速度变化曲线为梯形，过于理想化。因此深入研究工业机器人的能耗与其运动速度的关系，提出一套可行的控制策略很有必要。

工业机器人为六自由度串联机器人，其在工作过程中大部分能量由伺服电机及其驱动器消耗，而其腰关节、肩关节、肘关节的伺服电机功率最大，耗能最多。因此本文主要研究在工业机器人运动轨迹确定后，其腰关节、肩关节、肘关节的能耗与各个关节转速之间的关系，而当各个关节匀转速运动时，求解出此时各个关节的转速与总能耗的关系，根据关系式和约束条件，提出机器人能耗最小控制策略。

1　工业机器人动力学建模

机器人如图1所示，底座固定，腰部绕腰关节垂直方向轴线转动，大臂绕肩关节轴摆动，小臂绕肘关节轴转动。将机器人腰部、大臂、小臂等效简化为连杆机构，如图2所示。

图1　六自由度串联机器人　　　图2　机器人简化机构

机器人腰部的转动可由θ1描述，大臂的摆动可由θ2描述，小臂的转动可由θ3描述。将腰部、大臂、小臂末端的质量分别等效为m1、m2、m3，腰部、大臂、小臂的长度分别为d1、d2、d3。因此，工业机器人工作过程中动力学特性可由θ1、θ2、θ3描述。

由拉格朗日动力学方程知：

(1)

(2)

(3)

L=K-P

(4)

式中，T1为腰部末端所受力矩，T2为大臂末端所受力矩，T3为小臂末端所受力矩。

要通过拉格朗日方程求出机器人的动力学模型，需要求出机器人的动能K和势能P。

通过上述简化连杆机构求出工业机器人在工作过程中腰部、大臂、小臂的总动能为：

(5)

式中，J1、J2、J3分别为机器人腰部、大臂、小臂的转动惯量。

工业机器人腰部、大臂、小臂的总势能为：

(6)

将(5)、(6)式带入(1)、(2)、(3)、(4)式得出：

m3gd3sin(θ2+θ3)

(7)

所以，

(8)

(9)

A6=m3d2d3，A7=m2gd2+m3gd2,A8=m3gd3，

m3gd3。

因此，得出机器人腰部、大臂、小臂的动力学模型如上，其受各个关节的转动速度和转动加速度影响。

2　工业机器人能耗建模

2.1降低能耗一般方法

工业机器人在工作过程中的能耗主要与以下几点因素有关：机器人运动速度，机器人加减速大小及次数，运动轨迹，伺服电机的控制及电机的动态特性，控制器及有关电路等。其中，机器人的大部分能耗都由其中的伺服电机消耗。因此本节主要对伺服电机能耗建模，研究工业机器人的能耗与其各个关节的转动角速度的关系，并对机器人能耗进行优化。

目前降低机器人能耗的方法有如下几类[7-14]：①寻求机器人工作的最优路径；②减小机器人伺服电机的加减速大小及次数；③通过控制机器人的运动速度；④合理地安排机器人的动作状态的时间；⑤采用能量效率高的伺服电机；⑥采取其他的能耗最小的控制策略。本文主要研究通过控制机器人的运动速度来最小化其能量消耗。

2.2能耗分析

工业机器人中的电机通常采用交流伺服电机，交流伺服电机无电刷和换向器，工作比较可靠，对维护和保养要求低，且惯量小，易于提高系统的快速性，定子绕组散热亦比较方便，适应于高速大力矩工作状态。但是，电机的能耗占工业机器人总能耗很大一部分的比例，通过降低机器人伺服电机的能耗，能够切实有效地节省机器人的总能耗。随着电力电子技术的不断发展进步，交流伺服电机及其驱动器的效率不断提高，所以如果从电机硬件性能的方面去研究能耗，空间十分有限。我们可以寻找其他途径去降低机器人能耗。通过对机器人的工作轨迹进行优化，求出最优轨迹，可以降低机器人的能耗。而当机器人最优轨迹确定后，根据作业轨迹匹配轨迹点上的最佳运行速度，从而降低机器人能耗。由机器人动力学方程可以看出，惯性力作用居首，其做功是能耗的主要方式。机器人在加速或者减速过程中耗能最大，在匀速运动过程中耗能最小，应尽量避免机器人频繁的加减速，也可以通过合理安排机器人加减速及匀速运动的最优时间，从而降低机器人能耗。本文主要对机器人各个关节的转动角速度与能耗关系进行研究。

伺服电机主要是由定子和转子两大基本结构组成的。定子主要是用来作为电机的机械支撑和固定磁极，转子主要是用来感应电动势，从而实现电能和机械能的转换。转子在运动过程中受电磁转矩作用，交流伺服电动机的电磁转矩带动机械负载转动，电动机的转矩平衡方程式为：

Tem=TM+T0

式中，Tem为交流伺服电机电磁转矩，TM为电机轴上的输出转矩，等于机械负载制动转矩，T0是由机械损耗、铁芯损耗和杂散损耗引起的空载制动转矩。

由于工业机器人中电动机的机械损耗、铁芯损耗和杂散损耗引起的空载制动转矩比机械负载制动转矩要小的多，因此可以将空载制动转矩省略，所以得出：

Tem=TM

根据电动机的转矩特性得：

TM=Tem=CTφI=9.55CeφI

式中，CT为电机转矩常数，φ为电机每一磁极的总磁通量，I为电机电枢的电流，Ce为电机电势常数。

通过电动机的转矩特性公式可以求出电机机械负载制动转矩与电机电枢电流的关系，也就是可以求出机器人各个关节的力矩与其中的伺服电机电流的关系。由关系式：

TM=εMTi

式中，Ti为机器人腰部、大臂、小臂末端力矩，εM为腰关节、肩关节、肘关节减速器的输入转矩与输出转矩之比。

因此，可以分别得到机器人腰关节、肩关节、肘关节的电机电流：

(10)式中，I1、I2、I3分别为腰关节、肩关节、肘关节的电机电流，K1=9.55Ce1φ1，K2=9.55Ce2φ2，K3=9.55Ce3φ3，Ce1、Ce2、Ce3分别为腰关节、肩关节、肘关节的电机电势常数，φ1、φ2、φ3分别为腰关节、肩关节、肘关节中电机的每一磁极的总磁通量，εM1、εM2、εM3分别为腰关节、肩关节、肘关节的减速器的输入力矩与输出力矩之比。

(11)式中，P1、P2、P3分别为腰关节、肩关节、肘关节电机的机械功率，U2、U3分别为肩关节、肘关节电机的电压。

由公式(8)、(9)、(10)和(11)知消耗的总能量为:

(12)

公式(12)为机器人能耗目标函数，由此公式知：机器人肩关节、肘关节的转动角速度影响机器人稳定工作时的能耗，但转速受机器人最大转速的约束。此目标函数中含有两个未知量，且为多次项，通过MATLAB可以求解多变量方程的最小值。在计算过程中，需要考虑机器人最大转速的限制，同时考虑机器人的作业时间和运动的路径的约束。

3　机器人能耗最小控制策略及实验验证

3.1仿真分析

机器人的能耗主要分为两大部分：机械能耗和电气能耗。机械能耗主要包括伺服电机及其驱动器的能耗，而电气能耗主要包括机器人的控制器和一些电路的能耗。本文主要研究机器人的机械能耗，即研究机器人在匀速运动时，其中各个关节的转动角速度对能耗的影响。

本文选用埃夫特20KG机器人ER20-C10进行实验验证。m2=138kg，m3=95kg，d1=504mm，d2=780mm，d3=885mm。机器人ER20-C10中肩关节、肘关节的电机相同，肩关节、肘关节的转动角速度常用范围为0.93rad/s～1.86rad/s，工作电压为220V。在MATLAB中对机器人ER20-C10建模仿真，给定机器人肩关节、肘关节运动轨迹，并使机器人稳定运行2S，可以得出机器人的能耗与其肩关节、肘关节的转动角速度的具体关系，其关系图如图3所示。

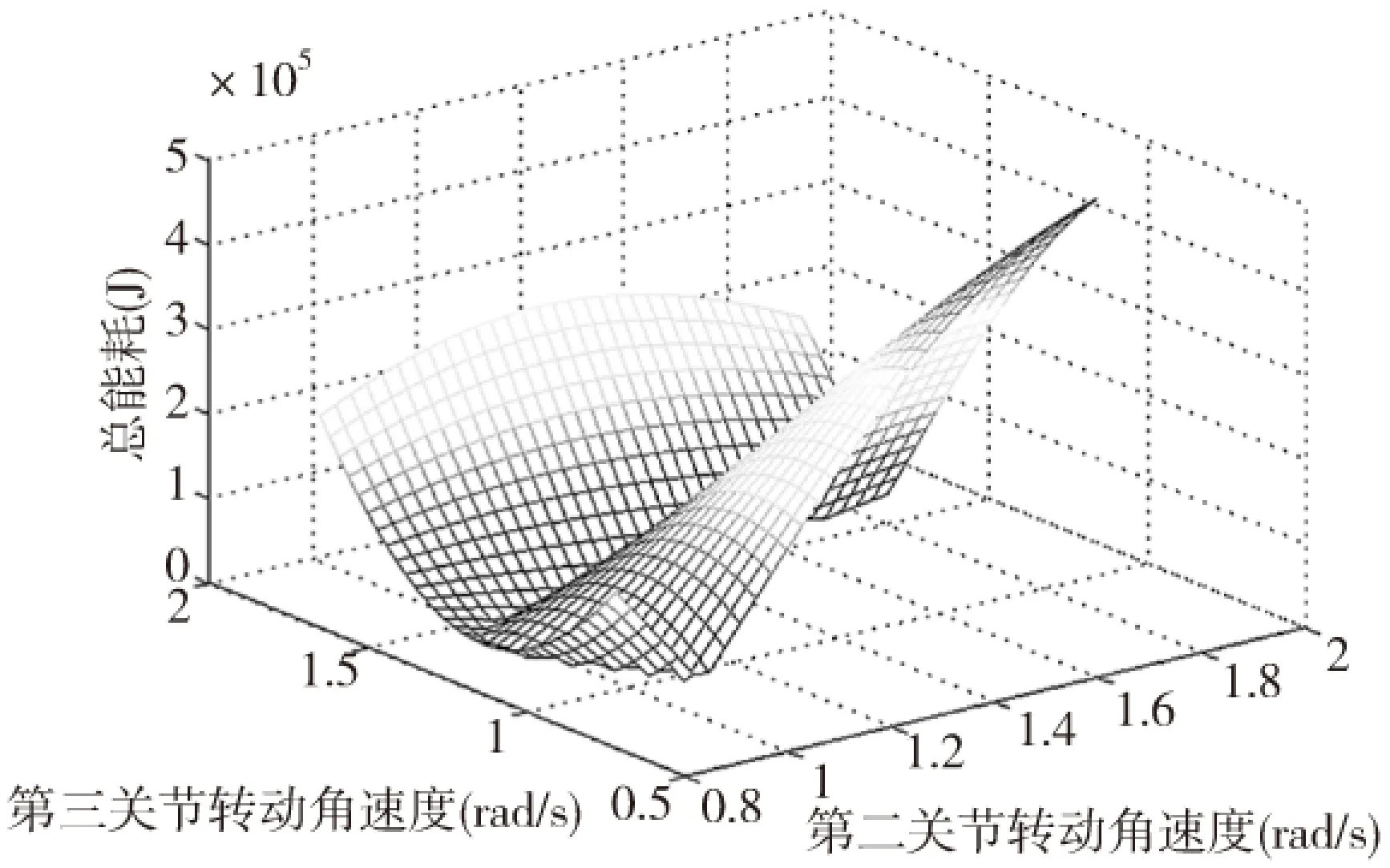
图3　机器人能耗与关节转动角速度关系图

3.2实验验算

将实验室中机器人ER20-C10的肩关节、肘关节沿上述指定的轨迹，以不同的转动角速度进行实验，分别测量其稳定运行后2s的功率大小。使用钳式功率计连接伺服电机控制器，可以直接测量机器人工作过程中各个伺服电机的输入功率大小，测出的数值为有效值，其接线图如图4所示。

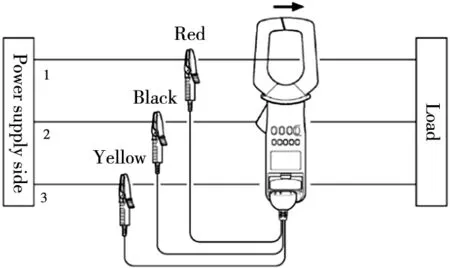
图4　钳式功率计接线图

利用钳式功率计测量的数据如表1所示。

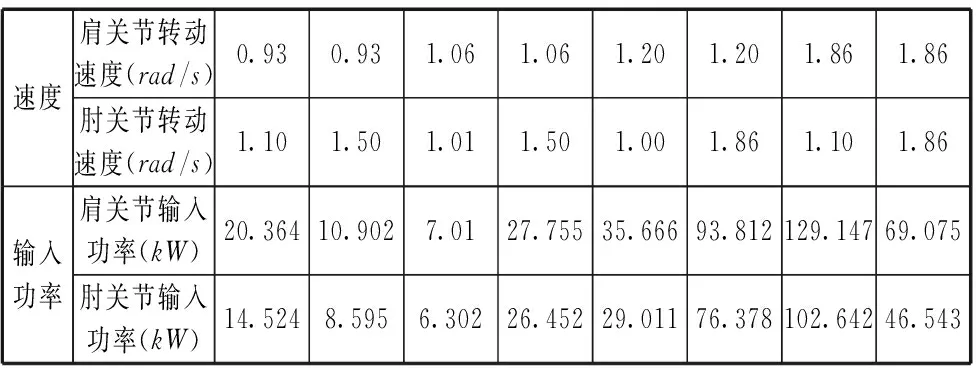
表1　肩、肘关节伺服电机的输入功率

由上表可知，在肩关节的转速为1.06rad/s，肘关节的转速为1.01rad/s时，机器人的肩关节、肘关节的总能耗最小，且为：

E′=(7010W+6302W)×2S×η×cosα=15974.4J

式中，η=0.75为伺服电机的能量效率，cosα=0.8为功率因数。

将表1中各速度分别带入式(12)中计算出机器人的理论能耗值，再通过表1中测量的功率值计算出机器人的实际能耗值，对比计算出实际值与理论值的误差，如表2所示。

表2　理论能耗值与实际能耗值误差

4　结束语

通过对工业机器人进行动力学和能耗建模，从而推导出机器人在匀速运动过程中能耗的目标函数，通过MATLAB仿真分析出机器人的能耗最小值，并通过实验测量出8组数据，计算分析出理论能耗值与实际能耗值误差不大，验证了优化策略的合理性。本策略也可以对其他类似的工业机器人能耗进行优化评价。但是，本文只是在对机器人匀速运动过程中的能耗进行优化，并没有考虑机器人的加减速情况。因此，还需要进一步研究机器人在加减速过程中的能耗最小控制策略。

[1] 孙敏，范守文．基于能耗指标的拟人机器人步态优化与分析[J]．机械设计与研究，2007，23(4):52-55．

[2] 霍炜，刘大维．基于局部最小能量的移动机器人路径规划[J]．青岛理工大学学报，2008，29(4):99-103．

[3]LEES，PARKJ，HAWC．Optimalcontrolofamackerel-mimickingrobotforenergyefficienttrajectorytracking[J]．JournalofBionicEngineering，2007，4( 4):209-215．

[4] 陈诚.基于能耗优化的六足机器人摆动腿轨迹规划[J]．计算机仿真，2015，32(1)：438-441.

[5]YamasakiF,HosodaK,AsadaM.Anenergyconsumptionbasedcontrolforhumanoidwalking[C].Proceedingsofthe2002IEEEInternationalConferenceonIntelligentRobotsandSystems,Lausanne,2002:2473-2477.

[6]DulebaI,SasiadekJZ.NonholonomicmotionplanningbasedonNewtonalgorithmwithenergyoptimization[J] .IEEETransactionsonControlSystemTechnology,2003,11(3):355-363.

[7] 王晓宇.两轮自平衡机器人的研究[D].哈尔滨：哈尔滨工业大学，2007.

[8] 党培，谭云福，申利民.基于多关机机器人的能量最小消耗控制策略[J].计算机应用研究，2010，27(12):4575-4577.

[9] 苗润龙.自主式水下机器人节能路径规划研究[D].哈尔滨：哈尔滨工程大学，2013.

[10] 徐海黎，解祥荣，庄健，等.工业机器人的最优时间与最优能量轨迹规划[J].机械工程学报，2010，46(9)：19-25.

[11] 金波，陈诚，李伟．基于能耗优化的六足步行机器人力矩分配[J]．浙江大学学报(工学版)，2012，46(7):1168-1174.

[12]ChongHuiKim,ByungKookKim.Energy-saving3-stepvelocitycontrolalgorithmforbattery-poweredwheeledmobilerobots[C].Proceedingsofthe2005IEEEInternationalConferenceonRoboticsandAutomation,Barcelona,2005:2375-2380.

[13]YongguoMei,Yung-HsiangLu,harlieHu,C.S.GeorgeLee.Energy-efficientmotionplanningformobilerobots[C].Proceedingsofthe2004IEEEInternationalConferenceonRoboticsandAutomation,NewOrleans,2004:4344-4349.

[14]AlbertoVergnano,CarlThorstensson,BengtLennartson,PetterFalkman,MarcelloPellicciari,ChengyinYuan,StephanBiller,FrancescoLeali.Embeddingdetailedrobotenergyoptimizationintohigh-levelscheduling[C].Proceedingsofthe2010IEEEInternationalConferenceonAutomationScienceandEngineering,Toronto,2010:386-392.

(编辑李秀敏)

MinimumEnergyConsumptionControlStrategyofWorkingProcessofIndustrialRobot

CAOPeng-fei1,2，XUDe-zhang1,2，WANGBu-yun1,2，ZHANGJia-min1,2，YANGWei-chao1,2

(1.SchoolofMechanical&AutomotiveEngineering,AnhuiPolytechnicUniversity,WuhuAnhui241000,China;2.AnpuInstituteofTechnologyRoboticsIndustryCo.,Ltd,WuhuAnhui241007，China)

Aimedattheproblemofhighenergyconsumptionintheprocessofindustrialrobots,aminimumenergyconsumptioncontrolstrategyofindustrialrobotwasproposed,itwastoeffectivelyreducethesixdegreeoffreedomseriesindustrialrobotenergyconsumptionintheprocessofworkingataconstantspeedunderthespecifiedpath.Basedondynamicsmodelingofindustrialrobotwaist,arm,forearm,themodelwasbuiltofenergyconsumptioninviewofthedrivemotoroftherobotwaistjoint,shoulderjoint,elbowjointoflargeenergyconsumption.Therobottargetenergyfunctionisdeducedthroughdynamicmodelandenergyconsumptionmodel,theminimumenergyconsumptioncontrolstrategywaspresentedaccordingtotheconstraint.Theeffectivenessofthecontrolstrategywasverifiedthroughmeasuringthemotorinputpoweroftheroboteachjointatdifferentrotationalspeed,bythetheoreticalandexperimentalenergyconsumptioncontrast.Thecontrolstrategycaneffectivelyreducetheoperationenergyconsumptionoftheindustrialrobot,energyconservationandefficiency,andithaduniversalityforindustrialrobot.

industrialrobot;dynamicsmodeling;energyconsumptionmodeling;minimumenergyconsumptioncontrolstrategy

1001-2265(2016)08-0157-04DOI:10.13462/j.cnki.mmtamt.2016.08.042

2015-08-27；

2015-09-22

国家自然科学基金资助项目(51175001)

操鹏飞(1990—)，男，安徽安庆人，安徽工程大学硕士研究生，研究方向为机器人机构与控制，(E-mail)563001142@qq.com。

TH166;TG659

A

Aug.2016