基于模糊切换增益调节的多电机同步控制算法的研究*
罗 亮,黄正良,刘知贵,程文雅
(西南科技大学 信息工程学院,四川 绵阳 621010)
基于模糊切换增益调节的多电机同步控制算法的研究*
罗亮,黄正良,刘知贵,程文雅
(西南科技大学 信息工程学院,四川 绵阳621010)
随着工业控制向着高速度、高精度、高可靠性方向发展,越来越多的多电机控制场合要求各电机间保持同步运行。针对现有的同步控制结构设计复杂,在线计算量大,不易拓展到大于2台电机以上的弊端。文章基于最小相关轴的控制思想,将多电机控制系统分解为相邻电机的控制,简化了结构设计,易于设计大于2台电机的控制结构。由于外部扰动是影响同步性能的重要因素,文中运用模糊切换增益调节的滑模控制方式,对不确定干扰项进行补偿。滑模控制保证了设计算法的鲁棒性,而模糊控制弱化了滑模算法的抖振作用。最后,在3台电机组成的多轴系统上进行仿真验证,结果表明该算法同步稳定性能好,抗干扰性强。
最小相关轴;模糊切换增益;多轴同步;耦合误差
0 引言
多电机的协调同步控制问题广泛存在于制造业与生产过程自动化控制系统中[1]。随着电力电子、计算机技术、现代控制理论等学科的发展,多电机同步控制的实现方式经历了从机械方式到电控方式的转变。传统的机械方式由于其控制结构固定、灵活性差、传动范围短、控制精度低等缺点使其使用受到很大的限制。最早的电控方式是以主从控制、并行控制为代表的非耦合同步算法,这些算法控制结构简单,容易实现,但是控制精度较低,不适用于精度较高的场合。Koren[2]首次将交叉耦合的算法运用到双轴控制系统中,通过耦合补偿调节两轴之间的误差,有效的改善了系统的同步性能。针对交叉耦合增益常数K难以确定的问题,文献[3]采用积分分离的PID算法对其进行改进,提高了系统的同步性能。随着被控同步电机台数的增多,交叉耦合控制日益凸显其难以拓展到两轴以上的弊端。在此基础之上,偏差耦合结构[4]通过引入速度补偿模块而得以实现结构的拓展。由于在偏差耦合控制结构中每个轴都要设计速度补偿器,使得计算复杂,控制律难以确定。为了简化控制结构,相邻交叉耦合[5]的控制算法被提出,并在多电机的同步控制中取得了良好的效果。除了在结构方面的改进,众多学者将智能算法运用到多电机的同步控制中。自适应以其实时性、强鲁棒性等优点得到广泛应用。文献[6]运用自适应的算法对电机的外部扰动进行补偿,取得了良好的同步性能。文献[7]将自适应逆控制运用到多线切割机的速度同步控制中,改善了同步性能。但是自适应算法需要不断的在线调整参数,进行辨识,设计复杂,稳定性证明繁琐。文献[8]将自适应PSD算法与单神经元PID算法相结合克服了单神经元PID增益固定的缺陷,提高了多电机的同步控制精度,但是神经网络的计算量大、不易保证闭环稳定性。滑模控制以其设计简单、鲁棒性强等优势被广泛运用在多轴同步控制中,但是其存在不可避免的斗振问题。
为了增强多轴同步控制的抗干扰能力,结合前人的研究成果,文中在最小相邻轴的结构基础上,运用模糊切换增益调节的滑模控制方式,对不确定干扰项进行补偿,使得线性化的耦合误差通过滑模面的设计稳定收敛,而模糊控制弱化了滑模算法的抖振作用。
1 最小相关轴的同步控制策略及控制参数
对于多电机(n>2)的控制系统中,各电机之间保持同步运行的控制目标是各电机的跟踪误差以及电机间的同步误差收敛到零。也即:
(1)

传统多电机同步误差为相邻电机间位置跟踪误差的差值:
(2)
由式(2)可知,如果所有电机均满足εi=0,则可实现多电机同步运行的性能。
如果在设计单个电机的控制律时,同时考虑其余各电机的位置误差影响因素,将导致沉重的在线计算负担。基于假设每相邻的一对电机同步,则可得到整个多电机控制系统的同步的控制思想。将相邻两轴定义为最小相关轴,控制每个电机的转速使这台电机的跟踪误差和与其相邻两电机的同步误差稳定收敛。即控制第i轴电机转速不仅使得ei(t)→0,而且保证(i-1)、i、(i+1)电机间保持同步。
为了更加直观方便的表示最小相关轴的作用机理,将同步误差重新定义为每个电机的跟踪误差与其两个相邻方向电机位置误差的差分值,如式(3)所示:
(3)
基于最小相关轴的控制思想,设计第i轴电机控制律时不仅要考虑ei(t),而且还要使得(i-1)、i、(i+1)电机间的同步误差为零。为了简化误差补偿器的设计,使其能够同时反馈位置误差和同步误差的作用,定义线性耦合误差如式(4)所示:
δi=ei+αεi
(4)
式(4)中α为耦合常数,用来权衡跟踪误差和同步误差之间的比重。α大小的选择对系统同步性能有很大的影响,选取α时尽可能的平衡两者的影响。
2 基于模糊切换增益调节的滑模控制设计
2.1伺服电机控制模型建立
三相交流伺服电机是一个非线性多变量系统。它包含了dq坐标系下定子电流分量id、iq以及电机角速度ω。如果对交流伺服电机采用id=0的矢量控制策略,则id=0始终成立。可得出系统状态方程:
(5)
由于该方程是线性解耦的,因此可得出三相交流伺服电机结构框图,如图1所示,其中Kt=1.5Pnψf表示电机电磁转矩系数,Ke=Pnf表示电机反电势系数[9]。

图1 交流伺服电机模型框图
交流伺服电机的动力学方程式如下:
X·(t)=AmX(t)+BmU(t)+CmTl
(6)

考虑系统参数可能的变化以及外部干扰的影响,式(6)可以重新写为:

(7)
假设系统满足匹配条件,则式(7)可简化为如下形式:
(8)
2.2滑模控制器设计
定义全局滑模面为:
s=δ·+cδ-F(t)
(9)
其中c>0,δ为定义的耦合误差。
为了保证系统状态处于滑模面、系统的闭环稳定性和滑模存在的条件,函数F(t)的设计必须满足①F(t)=δ·0+cδ0;②F(t)→0ast→∞;③F(t)一阶可导。为了使函数F(t)同时满足以上三个条件,设计F(t)为:
F(t)=s(0)exp(-λt)
(10)
其中λ>0,s(0)为初始时刻的s(t)。
设计滑模控制律为:
(11)

2.3模糊控制器设计
系统输入输出的模糊集分别定义如下:

(12)

(13)
控制系统的结构图如图2所示。

图2 模糊滑模控制系统结构图
2.4稳定性证明
定义Lyapunov函数为[11]:
(14)
(15)
将控制律式(11)代入式(15),化简可得:

(16)

(17)

(18)

3 仿真分析
3.1控制仿真模型
在本节中,将在三台电机的仿真平台上进行算法有效性验证。单个电机的控制模型如前文图1所示。在对所设计的结构分析之后,采用Simulink搭建控制系统的结构。最小相关轴系统的控制结构图如图3所示。

图3 最小相关轴控制系统仿真模型
3.2实验参数
在d-q坐标系下的三台电机的主要参数如表1。其中,参数Pe为电机的功率;Rs、Rr分别表示定子和转子的电阻;L1s、L1r、Lm分别表示定子绕组漏感,转子绕组漏感,定子和转子绕组互感;J表示转动惯量;p为极对数。

表1 三台电机的设置参数
3.3仿真条件及结果分析
考虑不确定项E(t)为高斯函数的形式:

(1)实验1
当系统输入阶跃信号时,参考信号会瞬间变化,系统在反馈环节的作用下,将试图把调节对象调节至新的平衡状态。在工程应用中,经常通过观察阶跃响应的性能来推测系统相关的控制特性。因此,为了验证设计算法的有效性,本文在三台电机的负载转矩相等的前提下,即Tl1=Tl2=Tl3=5N·m。设定速度参考指令为ω*=50rad/s,观察三台电机的阶跃响应曲线,并与PID算法进行仿真比较。

图4 模糊切换增益滑模控制算法阶跃响应曲线

图5 模糊切换增益滑模控制算法同步误差曲线

图6 PID控制算法阶跃响应曲线

图7 PID控制算法同步误差曲线
比较图4、图6的结果,可以看出本文的算法在阶跃响应过程中,无超调,且在0.2s左右达到设定的额定值。具有响应快,曲线收敛平滑的特性。从图5、图7的比较结果可以看出,在整个调节过程中,由于本文加入了线性耦合误差的作用, 电机能够快速有效的调节速度的变化,最大同步误差大大的减小了,并且同步误差在0.1s内收敛到零,系统具有良好的同步性能。
(2)实验2
由于负载突变对电机速度性能的影响最为显著,为了验证本文算法的优越性,在做负载突变试验时,假设电机控制的其它因素及现场通信与供电电源问题忽略不计,只考虑负载突变造成的同步误差。初始负载转矩都为5N·m,设定速度参考指令为ω*=20rad/s,仿真时间为t=2s,在t=1s时,三台电机的负载突变均增加为8N·m。

图8 负载突变下本文算法速度跟踪曲线

图9 负载突变下本文算法电机间同步误差曲线
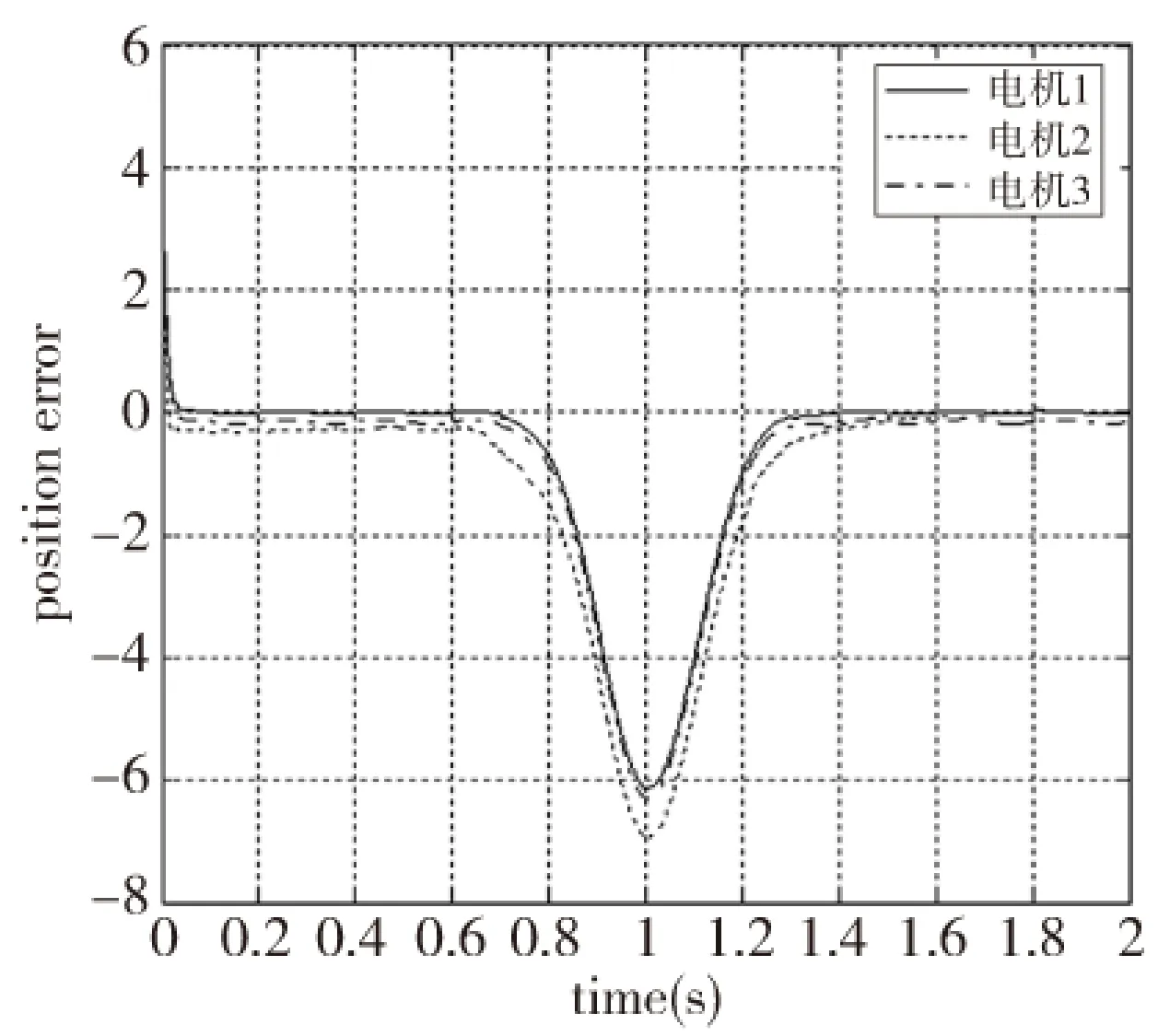
图10 负载突变下PID控制速度跟踪曲线

图11 负载突变下PID算法电机间同步误差曲线
从图8、图9中可以看到,所设计算法在外部扰动下能够快速响应, 各电机在控制器的作用下能够有效的跟踪变化,且保持一致的变化趋势,最大同步误差相较PID控制算法大大的减小了。系统通过调整保持同步运行,在t=1s发生突变之后,同步误差在t=1.1s左右再次快速收敛到零,在扰动的情况下仍能达到同步性能的控制要求,抗干扰能力得到了明显的提升。
4 结论
对多电机同步控制问题进行研究之后,在最小相关轴的控制结构基础之上,运用模糊切换增益滑模控制算法在伺服电机控制模型搭建的仿真平台验证之后,分析结果得出如下结论:
(1)各电机的跟踪误差对系统的同步精度影响最明显,有效的权衡电机之间的误差变化能够提高电机间的同步性能。
(2)控制结构设计的繁易程度直接关系同步控制误差,避免运用非线性积分误差,造成累计误差的作用。充分利用线性化耦合误差来简化结构的设计,提高补偿效率。
(3)电机固有参数是否相同影响多轴的同步性能,在其他条件完全相同的情况下,参数相同的电机能够在更短时间内达到同步。
[1] 丛爽,刘宜. 多轴协调运动中的交叉耦合控制[J]. 机械设计与制造,2006(10):166-168.
[2] 潘军. 基于交叉耦合策略的多指手控制方法的研究[D]. 哈尔滨:哈尔滨工业大学, 2010.
[3] 程文雅, 罗亮, 刘知贵. 基于多轴同步滑模控制的积分分离PID算法的研究[J]. 组合机床与自动化加工技术, 2015(8):97-100.
[4]YangG,ZhangJ.SynchronizationControlinVerticalShipLiftBasedonRelativeCouplingStrategy[M].Berlin:PracticalApplicationsofIntelligentSystems,SpringerBerlinHeidelberg, 2014.
[5] 高恒路, 桑勇, 邵龙潭. 同步控制策略及其典型应用的研究[J]. 液压气动与密封, 2012, 32(5): 1-7.
[6] 徐攀, 徐为民, 谭莹莹,等. 基于自适应扰动补偿的多电机时变滑模控制[J]. 控制工程, 2013,20(S0):218-222,227.
[7] 江丽. 多线切割机多轴系统的速度同步控制研究[D]. 武汉:武汉理工大学, 2013.
[8] 崔皆凡, 刘艳, 李玥,等. 基于PSD算法的神经元PID多电机同步控制[J]. 机床与液压, 2013,41(19):18-21.
[8]CuiJiefan,LiuYan,LiYue,etal.SynchronouscontrolofmultimotorbasedonPSDalgorithmPID[J].Machinetoolandhydraulic, 2013 (19): 18-21.
[9] 季明逸. 多轴同步控制策略的研究与实践[D]. 南京:南京航空航天大学, 2012.
[10]WeifaP,DezongZ.SpeedSynchronizationofMultiInductionMotorswithTotalSlidingModeControl[C]//PowerandEnergyEngineeringConference(APPEEC), 2010Asia-Pacific.IEEE, 2010:1-9.
[11] 刘金琨, 孙富春. 滑模变结构控制理论及其算法研究与进展[J]. 控制理论与应用, 2007, 24(3):407-418.
(编辑李秀敏)
BasedonFuzzySwitchingGainAdjustmentresearchonSynchronizationControlAlgorithmofMultiMotor
LUOLiang,HUANGZheng-liang,LIUZhi-gui,CHENGWen-ya
(SchoolofInformationEngineering,SouthwestUniversityofScienceandTechnology,MianyangSichuan621010,China)
Withthedevelopmentofindustrialcontrolinthedirectionofhighspeed,highprecision,highreliability,moreandmoremultimotorcontroloccasionsrequiresynchronousbetweenmotors.Inviewoftheexistingsynchronouscontrolstructureexitingthedisadvantages:thecomplexdesignofstructure,thelargeonlinecomputation,andnoteasytoextendtothecontrolstructureofmorethan2motors.Inthispaper,basedonthecontroltheoryoftheleastcorrelationaxis,thecontrolsystemofthemultimotorsisdecomposedintothecontroloftheadjacentmotors,thestructuredesignissimplified,andthecontrolstructureiseasytodesign.Duetotheinterferencedisturbanceisanimportantfactorforthesynchronizationperformance.Inthispaper,usingfuzzyswitchinggainadjustmentoftheslidingmodecontroltocompensatetheuncertaindisturbance.Slidingmodecontrolensurestherobustnessofdesignedalgorithmandfuzzycontroltoweakenthechatteringeffectofslidingmodealgorithm.Finally,thesimulationresultsshowthatthealgorithmhasgoodsynchronousstabilityperformanceandgoodinterferenceimmunityinthemultiaxissystemcomposedof3motors.
leastcorrelationaxis;fuzzyswitchinggain;multi-axissynchronous;cross-couplingerror
1001-2265(2016)08-0085-04DOI:10.13462/j.cnki.mmtamt.2016.08.024
2016-03-14
四川省教育厅科技项目“基于ZynqSoC的六轴四联动焊锡机器人专用控制器设计”(16ZB0145);四川省研究生教育改革创新项目“控制工程专业学位硕士研究生教育实践基地建设”(14JGCX01)
罗亮(1977—),男,湖南耒阳人,西南科技大学讲师,研究方向为嵌入式系统研究与装备控制器研发,(E-mail)17632540@qq.com;黄正良(1962—),男,湖南益阳人,西南科技大学教授,博士生导师,研究方向为控制理论和计算机应用技术研究;刘知贵(1966—),男,四川射洪人,西南科技大学教授,博士生导师,研究方向为控制理论和计算机应用技术研究。
TH166;TG659
A

