带空移动的加权有限自动机量化等价及其转换

汪 国 武

(安徽工程大学计算机与信息学院　安徽 芜湖 241000) (安徽工程大学计算机应用技术重点实验室　安徽 芜湖 241000)



带空移动的加权有限自动机量化等价及其转换

汪 国 武

(安徽工程大学计算机与信息学院安徽 芜湖 241000) (安徽工程大学计算机应用技术重点实验室安徽 芜湖 241000)

在经典的有限自动机理论中，带空移动的有限自动机与不带空移动的有限自动机是等价的。取值于实数的加权有限自动机是自动机的一种推广模型，它给经典自动机的每个转换赋一个取值于实数的权值，这些权值表示执行转换的代价。为了研究带空移动的加权有限自动机与不带空移动的加权有限自动机是否具有等价性这一问题，提出量化等价的概念，并研究如何将一个带空移动的加权有限自动机转换为一个与之量化等价的不带空移动的加权有限自动机。研究结果表明：这两者是量化等价的。

量化等价不确定的有限状态自动机加权自动机形式化验证

0　引　言

在计算机科学中，有限状态自动机[1,2]是自动机理论的研究对象，广泛地被应用于神经网络、模式识别、密码算法、形式化分析与验证等领域中。关于有限状态自动机，一个有趣的结论是：带空移动和不带空移动的自动机具有等价性，即如果一个正则语言能被一个带空移动的自动机接受，那么该语言可被一个不带空移动的自动机接受。

经典的有限自动机是一种对系统进行定性的建模方法，它明确规定了所建模的系统所具有的性质和不具有的性质。为了对计算机系统的量化信息进行建模，研究者提出了很多能描述量化信息的自动机模型[3-7]，模糊自动机[8,9]是其中一个比较有代表性意义的自动机的推广模型。文献[10]讨论了带空移动的模糊自动机和模糊自动机等价的充分必要条件；文献[11]证明了带空移动的不确定性模糊自动机和不确定性模糊自动机具有等价性。

取值于实数的加权有限自动机[12-15]是自动机的另一种推广模型，该模型已经被用于嵌入式系统的设计和验证[16,17]。取值于实数的加权有限自动机的基本特点是：通过给经典自动机的每个转换赋一个取值于实数的权值，这些权值表示执行转换的代价，如花费的时间或消耗的资源，或者表示为成功执行的几率等。对取值于实数的加权有限自动机的研究已经取得较大的进展， 但前文提到的结论：带空移动和不带空移动的自动机具有等价性，到目前为止还没有在加权有限自动机这种模型上进行研究。

本文首先提出带空移动的加权有限自动机；接着为了描述带空移动的加权有限自动机和不带空移动的加权有限自动机的等价性，我们提出量化等价的概念；然后在量化等价的基础上，研究和探讨如何将一个带空移动的加权有限自动机转换为一个与之量化等价的不带空移动的加权有限自动机。

1　带空移动的加权有限自动机

首先介绍加权有限状态自动机、带空移动的加权有限状态自动机及其识别的语言和量化语言等，然后引入量化等价的概念。

设Q是一个集合，记P(Q)为Q的幂集。后文R+表示非负实数集。

定义1一个加权有限(状态)自动机[14]WFA(weighted finite automaton)M是一个8元组：

M=(Q,Σ,δ,qI,F,γ,i,f)

其中：

(1) Q：非空有穷状态集合。对于任意q∈Q，称q是M的一个状态。

(2) Σ：输入有限字母表。

(3) δ：δ⊆Q×Σ×Q是一个转换关系。

(4) qI：qI∈Q是一个初始状态。

(5) F：F⊆Q是终止状态集合，对于任意q∈F，称q为M的终止状态。

(6) γ：δ→R+是一个加权函数。如果转换(q,a,q′)∈δ，相应的权函数为γ(δ(q,a,q′))，表示M在状态q读入字母a后到达状态q′时，需要的代价为γ(δ(q,a,q′))。

(7) i：qI→R+是初态权函数，初始状态qI的权值为i(qI)。

(8) f：F→R+是终态权函数，如果对于任意q∈F，则终态q的权值为f(q)。

我们常用q′∈δ(q,a)表示(q,a,q′)∈δ。另外，我们记δ(q,a)={q′:(q,a,q′)∈δ}。为了符号简便，后文γ(δ(q,a,q′))记为γ(q,a,q′)。类似地，我们也将γ(δ(q,a))简写为γ(q,a)，γ(q,a)={q′/γ(q,a,q′):q′∈δ(q,a)}是一个权函数的集合，其元素表示为q′/γ(q,a,q′)，目的是清楚地表明权函数值γ(q,a,q′)对应转换到达的目标状态为q′。

加权有限自动机与经典的有限自动机的区别是：加权有限自动机对每个转换定义了相应的转换代价，称为权函数。此外，对于每个初始状态和接受状态也都定义了权值。

为了定义加权有限自动机的接受语言，将δ扩充为δ⊆P(Q)×Σ×P(Q)，对于P⊆Q,a∈Σ，定义：

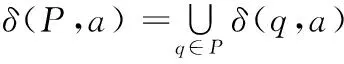
进一步将δ扩充为δ⊆Q×Σ*×P(Q)，对于任意q∈Q,w∈Σ*,a∈Σ，作如下定义：

δ(q,ε)={q}

定义2设M=(Q,Σ,δ,qI,F,γ,i,f)是一个WFA。M所接受(识别)的语言L(M)定义为：

L(M)={x:x∈Σ*且δ(qI,x)∩F≠∅}

不难看出，加权自动机的接受语言的定义与经典的自动机接受语言定义类似，然而加权自动机不仅能描述所识别的字符串，而且还能给出每个识别字符串的权重。

同样地，我们也对权函数γ进行相应的扩展， 对于任意q∈Q,w∈Σ*,a∈Σ，定义：

γ(δ(q,ε,q))=0

(1)

γ(δ(q,wa,q′))=min{γ(δ(q,w,p))+

γ(δ(p,a,q′)):p∈δ(q,w)}

(2)

其中，式(2)表示：所有从状态q出发先处理w后到达某一状态，然后经由该状态识别a到达状态q′的运行过程的权值之和组成的集合的最小元素值。

定义3设M=(Q,Σ,δ,qI,F,γ,i,f)是一个WFA，x∈L(M)。x被M接受的权值定义为：

W(M,x)=i(qI)+min{γ(δ(qI,x,qf))+f(qf):qf∈(δ(qI,x)∩F)}

下面我们用例子去阐述以上的定义。

例1如图1所示，一个WFAM=({q0,q1,q2,q3},{a,b,c,d},δ,q0,{q3},γ,i,f)，其中转换关系δ表示如下：

δ(q0,a)={q0,q1,q2}δ(q0,b)={q1,q2}δ(q0,c)={q2}

δ(q0,d)={q3}δ(q1,b)={q1,q2}δ(q1,c)={q2}

δ(q1,d)={q3}δ(q2,c)={q2}δ(q2,d)={q3}

相应的权函数γ表示如下：

γ(q0,a)={q0/7,q1/8,q2/11}γ(q0,b)={q1/9,q2/11}

γ(q0,c)={q2/11}γ(q0,d)={q3/13}

γ(q1,b)={q1/8,q2/10}γ(q1,c)={q2/11}

γ(q1,d)={q3/12}γ(q2,c)={q2/9}γ(q2,d)={q3/10}

初始状态的权值：i(q0)=2，终态权函数：f(q3)=1。

显然，acd∈L(M)，因为δ(q0,acd)∩F={q3}≠∅。据此，我们有：

γ(q0,acd,q3)=min{γ(q0,ac,q2)+γ(q2,d,q3)}

=min{min{(γ(q0,a,q2)+γ(q2,c,q2)),

(γ(q0,a,q1)+γ(q1,c,q2))}+10}

=min{min{(11+9),(8+11)}+10}

=min{19+10}=29

根据定义3，我们可以得到：

W(M,acd)=i(q0)+min{γ(q0,acd,q3)+f(q3)}

=2+min{29+1}

=32

所以，acd被M接受的权值为32。

现在我们引入另一种加权有限自动机模型，带空移动的加权有限状态自动机，如图1所示。

图1　不带ε移动的WFA

定义4一个带空移动的加权有限自动机ε-WFA(weighted finite automata with ε-moves)M′是一个8元组：

M′=(Q,Σ,δ,qI,F,γ,i,f)

其中，Q,Σ,qI,F,γ,i,f的意义与定义1相同，所不同的是转换关系δ⊆Q×(Σ∪{ε})×Q。也就是说，对于q∈Q，允许q做一个空移动(ε移动)而到达其他的状态。

类似地，下面我们将δ扩充为δ*⊆Q×Σ*×Q，对于P⊆Q,q∈Q，w∈Σ*,a∈Σ，定义：

ε-closure(q)={p:状态q经若干个ε可达p}

(3)

δ*(q,ε)=ε-closure(q)

(4)

(5)

δ*(q,wa)=δ*(δ(δ*(q,w),a),ε)

(6)

其中，式(6)表示：从状态q出发先处理w后到达某一状态，然后经由该状态识别a到达的状态集合。特别地，当w=ε时，我们有：δ*(q,a)=δ*(δ(δ*(q,ε),a),ε)。

定义5设M′=(Q,Σ,δ,qI,F,γ,i,f)是ε-WFA，则M′所识别的语言：

L(M′)={x:x∈Σ*且δ*(qI,x)∩F≠∅}

同样地，我们也对ε-WFA的权函数γ扩展为γ*:δ*→R+， 对于任意q∈Q,w∈Σ*,a∈Σ，定义：

γ*(δ*(q,a,p))=min{γ(δ(q,a,p)):(q,a,p)∈δ*}

(7)

γ*(δ*(q,wa,q′))=min{γ*(δ*(q,wp))+

γ*(δ*(p,a,q′)):p∈δ*(q,w)}

(8)

其中，式(8)表示：从状态q出发先处理w后到达某一状态，然后经由该状态识别a到达状态q′的运行过程的权值之和，包含了计算空字符ε的权值。相同的字符串有多个权值，取最小值。

例2如图2所示，M′是一个ε-WFA，求γ*(δ*(q0,bd,q3))值。

图2　带ε移动的WFA

由于：

δ*(q0,b)=δ*(δ(δ*(q0,ε),b),ε)

=δ*(δ({q0,q1,q2},b),ε)

=δ*({q1},ε)={q1,q2}

所以：

γ*(δ*(q0,b,q1))=min{γ(δ(q0,b,q1))}

=min{γ(q0,ε,q1)+γ(q1,b,q1)}

=min{1+8}=9

同理可得，γ*(δ*(q1,d,q3))=12，γ*(δ*(q0,b,q2))=11，γ*(δ*(q2,d,q3))=10。

因此：

γ*(δ*(q0,bd,q3))=min{(γ*(δ*(q0,b,q1))+γ*(δ*(q1,

d,q3))),(γ*(δ*(q0,b,q2))+

γ*(δ*(q2,d,q3)))}

=min{(9+12),(11+10)}=21

定义6设M′=(Q,Σ,δ,qI,F,γ,i,f)是一个ε-WFA，x∈L(M′)。x被M′接受的权值为：

W(M′,x)=i(qI)+min{γ*(δ*(qI,x,qf))+f(qf):

qf∈(δ*(qI,x)∩F)}

例3如图2所示，M′是一个ε-WFA,显然有：bd∈L(M′)，因为δ*(q0,bd)∩F={q3}≠∅，根据定义6，我们可知：

W(M′,bd)=i(q0)+min{γ*(δ*(q0,bd,q3))+f(q3)}

=2+min{21+1}

=24

因此，bd被M′接受的权值为24。

以下我们给出一个判断两个加权自动机是否等价的标准：

定义7设任意两个WFAM和M′，如果有L(M)=L(M′)且当x∈L(M)时有W(M,x)=W(M′,x)，那么就称M和M′量化等价。

2　量化等价

在经典有限自动机理论中，对于任意一个带空移动的有限自动机，可以构造一个等价的不带空移动的有限自动机，使得两者识别的语言相同。那么，对于加权自动机是否也有类似的结论。也就是说，对于任意一个ε-WFAA，是否存在一个与之量化等价的WFAB是下文将研究解决的问题。

为了解决这个问题，我们来探讨WFAB的构造过程。我们注意到，ε-WFAA和WFAB的区别在于前者允许有空移动，而对于一个语言的句子来说，除非ε单独作为一个句子，否则空移动ε不会影响句子本身。所以，考虑将A在识别句子过程中遇到类似于ε*aε*(a的前后各有若干个ε，a∈Σ)的字符串时，在B中用一个输入字符为a的非空转换替换。此外，如果ε-WFA的语言中包含句子ε，则将B的初始状态同时也设为终态，让B也可以识别句子ε，这样可保证L(A)=L(B)成立。另一方面，在构造B时，使得B中的输入字符a的权值等于A中串ε*aε*的权值之和，那么也可以保证W(A,x)=W(B,x)成立。也就是说，由于W(A,x)表示x在其运行路径上的所有转换的权值之和，如果构造WFAB，满足使B的每一次转换的输入字符a(a≠ε)及其权函数γ的值都与A相同，那么必有L(A)=L(B)且W(A,x)=W(B,x)成立。

命题1设A=(Q,Σ,δA,qI,FA,γA,i,fA)是一个ε-WFA。我们构造一个WFAB=(Q,Σ,δB,qI,FB,γB,i,fB)如下：

(1) 对于A中的Q，Σ，qI，i在B中保持不变。

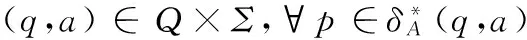
(3) 终态集FB：如果ε∈L(A)，FB=FA∪{qI}，否则FB=FA。

(4) 终态权函数fB：如果ε∈L(A)时，fB(qI)=W(A,ε)-i(qI)，否则，对于所有q∈FA，使fB(q)=fA(q)。

那么，对于A和B有以下结论成立：

(1) L(A)=L(B)；

(2) 对于任意x∈L(A)，有W(A,x)=W(B,x)。

证明对于结论1的证明，参见文献[3]。下面证明结论2成立。为此，我们需要先证明以下的结论1和结论2成立。

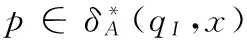
首先我们用数学归纳法证明结论1成立。

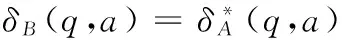
2) 假定|x|=n时，上式成立。当|x|=n+1时，不妨设x=wa，这里|w|=n,a∈Σ，则有：

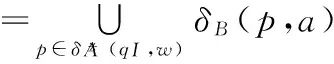
构造步骤(2)

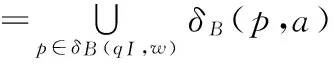
归纳假设

=δB(qI,wa)

因此当|x|=n+1时，结论1成立。

接下来，我们也用数学归纳法证明结论2成立。

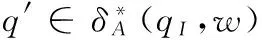
γB(δB(qI,x,p))=γB(δB(qI,wa,p))

=min{γB(δB(qI,w,q′))+γB(δB(q′,a,p)):

q′∈δB(qI,w)}

=min{γB(δB(qI,w,q′))+γB(δB(q′,a,p)):

结论1

归纳假设

构造步骤(2)

由1)、2)可得，结论2成立。

现在我们可以证明：对于任意x∈L(A)，有W(A,x)=W(B,x)成立。同样用数学归纳法证明。

1) 当|x|=0时，即当x=ε的情况：

W(B,ε)=i(qI)+γ(δ(qI,ε,qI))+f(qI)

=i(qI)+f(qI)

=i(qI)+W(A,ε)-i(qI)

构造步聚(4)

=W(A,ε)

所以，当ε∈L(A)时，结论W(A,ε)=W(B,ε)成立。

2) 当|x|≥1时，即当x≠ε的情况：

=i(qI)+min{γB(δB(qI,x,p))+fA(p):p∈

结论2

=i(qI)+min{γB(δB(qI,x,p))+fA(p):p∈

(δB(qI,x)∩FA)}

结论1

=i(qI)+min{γB(δB(qI,x,p))+fA(p):p∈

(δB(qI,x)∩FB)}

步骤(3)

=i(qI)+min{γB(δB(qI,x,p))+fB(p):p∈

(δB(qI,x)∩FB)}

步骤(4)

=W(B,x)

定义3

所以，对于∀x∈L(A)(x≠ε)，有W(A,x)=W(B,x)成立。

综合1)和2)得到：∀x∈L(A)，W(A,x)=W(B,x)成立。

根据以上结论，我们得到本文一个主要结论 。

定理1任意一个ε-WFA总存在一个与之量化等价的WFA。

表1　ε-WFA A中的δ*和γ*

3　算　法

前文介绍了如何将ε-WFA转换成与之量化等价的WFA，下面探讨转换的算法实现。根据构造过程可知，构造WFA的主要任务是构造步骤(2)：对于ε-WFA中所有的(q,a)∈Q×Σ，计算出δ*(q,a)=δ*(δ(δ*(q,ε),a),ε)和相应的γ*(δ*(q,a))值。据此，设计出相应的转换算法，如算法1所示：

算法1ε-WFA2WFA算法

输入：ε-WFAA=(Q,Σ,δ,qI,F,γ,i,f)

输出：WFAB=(Q,Σ,δ′,qI,F′,γ′,i,f′)

1:F′=F;f′=f;δ′=∅;

2:γ′=∅;

3:forall{q∈Q}

4:forall{a∈Σ}

5:InitQueue(W);InitQueue(W′);

6:Enqueue(W,);

//添加初始项，使W≠∅

7:while(W≠∅)do

8:=Dequeue(W);

//这里α一定为ε

9:ifδ(q2,ε)≠∅then

10:forall{q3∈δ(q2,ε)}

11:v=v+γ(q2,ε,q3);

12:Enqueue(W,);

13:ifq3∈Fthen

14:F′=F∪{qI};f′(qI)=v-i(qI);

15:else//δ(q2,ε)=∅，即q2后不含空移动

16:Enqueue(W′,);

17://此时，W′中存放的元素,q2∈δ*(q,ε)

18:while(W′≠∅)do

19:=Dequeue(W′);

20:ifα=ε&δ(q2,a)≠∅then

21:forallq3∈δ(q2,a)

22:δ′=δ′∪{δ(q,a,q3)};v1=v1+γ(q2,a,q3);

23:γ′=γ′∪{v1=γ(q,a,q3)};

24:Enqueue(W,);

25://此时，W中存放元素,q2∈δ(δ*(q,ε),a)

26:while(W≠∅)do

27:=Dequeue(W);

28:ifδ(q2,ε)≠∅then

29:forall{q3∈δ(q2,ε)}

30:v=v+γ(q2,ε,q3);Enqueue(W,);

31:δ′=δ′∪{δ(q,a,q3)};γ′=γ′∪{v=γ(q,a,q3)};

我们轮流使用2个工作队列W和W′，队列的每一个元素中存放转换函数及相应的权值，任一元素共有4个参数组成。其中前3个参数表示转换函数(q,α,q2)∈δ，第4个参数为转换的权值v=γ(q,α,q2)，这里q,q2∈Q,α∈(Σ∪{ε})。

算法的第5行对队列W和W′作初始化，第6行给W添加一个特殊元素，使得其后的循环条件W≠∅成立。

算法的第7-16行，主要利用队列W由q求算δ*(q,ε)，存入W′。重复从队列W中取出每一个元素(第8行)：如果该元素(转换)的后继转换仍为带空移动的转换时(第9行)，则将后继入队(第12行)，在此过程中，若到达了终态(第13行)则将qI置为终态并设定终态权值(第14行)，这段代码对应构造过程的步骤(3)和(4)；否则，意味着完成了δ*(q,ε)计算，则将元素转移到W′中保存(第15、16行)，循环结束后W′中存放的元素为：，满足q2∈δ*(q,ε)。

算法的第18-24行，从W′中取出所有元素即转换δ*(q,ε)(第19行)，求算δ(δ*(q,ε),a)，存入队列W中。

算法的第25-31行，从W中取出所有元素即转换δ(δ*(q,ε),a)(第27行)，求算δ*(δ(δ*(q,ε),a),ε)，结果存入队列W中。

整个算法围绕求算δ*(q,a)=δ*(δ(δ*(q,ε),a),ε)和γ*(δ*(q,a))之值，在这个过程中完成对F′、f′、δ′、γ′的构造。

复杂度分析我们注意到算法主要是处理队列中的元素，算法的复杂度主要由入队的次数决定，即由语句Enqueue(W,)决定。该语句在算法中共出现4次，12行、16行、24行和30行。在不考虑外层循环(第3、4行)的情况下，第12行最多执行|Q|2次，因为满足循环条件的状态q3(第10行)最多有|Q|个，而且这些元素中的任意一个也可能有|Q|个带空移动的转换需要加入到队列W中；第16行也最多执行|Q|2次，因为该行只是将W中所有元素转移至W′中；第24行最多执行|Q|次，因为满足循环条件的状态q3(第21行)最多有|Q|个；第31行最多执行|Q|2次，原因同第12行。共执行3|Q|2+|Q|次，考虑外层循环，总共|Q|·|Σ|·(3|Q|2+|Q|)次。所以时间复杂度为O(|Q|3·|Σ|)。

4　结　语

本文针对加权自动机的等价性问题提出了量化等价的概念，研究和探讨如何将一个带空移动的加权有限自动机转换为一个与之量化等价的不带空移动的加权有限自动机，研究结果表明转换前后两者是量化等价的。

[1] Hopcroft J E,Ullman J D.Introduction to Automata Theory,Languages,and Computation[M].MA:Pearson Education India,1979.

[2] 蒋宗礼.形式语言与自动机理论[M].2版.北京:清华大学出版社,2007.

[3] 张晋津.转换系统行为近似等价性的研究[D].南京航空航天大学,2010.

[4] 潘海玉.状态转化系统的格值量化验证方法研究[D].上海:华东师范大学,2012.

[5] Pan H Y,Cao Y Z,Zhang M,et al.Simulation for lattice-valued doubly labeled transition systems[J].International Journal of Approximate Reasoning,2014,55(3):797-811.

[6] Pan H Y,Zhang M,Wu H Y,et al.Quantitative analysis of lattice-valued Kripke structures[J].Fundamenta Informaticae,2014,135(3):269-293.

[7] Pan H Y,Li Y M,Cao Y Z.Lattice-valued simulations for quantitative transition systems[J].International Journal of Approximate Reasoning,2015,56(2):28-42.

[8] 李永明.模糊系统分析[M].北京:科学出版社,2005.

[9] Li Y M.Finite automata theory with membership values in lattices[J].Information Sciences,2011,181(5):1003-1017.

[10] Li Z H,Li P,Li Y M.The relationships among several types of fuzzy automata[J].Information Sciences,2006,176(15):2208-2226.

[11] Cao Y Z,Yoshinori E.Nondeterministic fuzzy automata[J].Information Sciences,2012,191(15):86-97.

[12] Chatterjee K,Doyen L,Henzinge T.Quantitative languages[J].ACM Transactions on Computational Logic,2010,11(4):1-38.

[13] Chatterjee K,Doyen L,Henzinger T A.Expressiveness and closure properties for quantitative languages[J].Logical Methods in Computer Science,2010,6(3):199-208.

[14] Aminof B,Kupferman O,Lampert R.Rigorous approximated determinization of weighted automata[J].Theoretical Computer Science,2013,480(8):104-117.

[15] Boker U,Henzinger T.Exact and approximate determinization of discounted-sum automata[J].Logical Methods in Computer Science,2014,10(1):1-33.

[16] 黄明璋,李国强.基于模型检测的并发程序分析综述[J].计算机应用与软件,2014,31(12):1-6,24.

[17] 袁志斌.Büchi自动机的优化综述[J].计算机应用与软件,2010,27(6):32-34,88.

QUANTITATIVE EQUIVALENCE OF WEIGHTED FINITE AUTOMATA WITH ε-MOVES AND ITS TRANSITION

Wang Guowu

(SchoolofComputerandInformation,AnhuiPolytechnicalUniversity,Wuhu241000,Anhui,China) (KeyLaboratoryofComputerApplicationTechnology,AnhuiPolytechnicUniversity,Wuhu241000,Anhui,China)

In classical finite automaton theory, the finite automaton with ε-moves and normal finite automaton are equivalent. The weighted finite automaton valued in real numbers is an extension model of automaton, it assigns one weight valued in real numbers to every transition of classical automaton, these weights denote the cost of transitions execution. To study whether the finite automaton with ε-moves and the normal finite automaton are equivalent, we introduce the concept of quantitative equivalence, and give a method of how to transform a weighted finite automaton with ε-moves to a normal weighted finite automaton in quantitative equivalence with the former. Study result shows that these two are quantitatively equivalent.

Quantitative equivalenceNondeterministic finite automataWeighted automataFormal verification

2015-01-23。国家自然科学基金项目(61300170)；安徽省教育厅自然科学基金项目(KJ2013B020)；安徽省优秀青年人才基金重点项目(2013SQRL034ZD)。汪国武，讲师，主研领域：形式化分析与验证。

TP301.1

A

10.3969/j.issn.1000-386x.2016.08.005