混合系数线性模型h-K型岭估计的改进研究

余新宏，吴　坚（安徽农业大学 经济技术学院，安徽 合肥 230011）

混合系数线性模型h-K型岭估计的改进研究

余新宏，吴坚①
（安徽农业大学 经济技术学院，安徽 合肥 230011）

文章对病态的混合系数线性模型Z（t）=［X（t）］′α+［Y（t）］′β提出一类新的估计h-K型估计，讨论此种估计的相关性质，利用Stein式压缩技术证明了可以改进岭估计（在均方误差意义下）；同时给出参数的最优值满足的条件，证明h-K型岭估计的可容许性.

混合系数线性模型；h-K型估计；岭估计；Stein估计；可容性

0　引言

混合系数线性模型在经济分析、可靠性退化分析及其生物学等领域有着广泛的应用，此模型的线性参数部分是固定的，另一部分是随机的.

一般地，考虑混合系数线性模型［1］形式如下

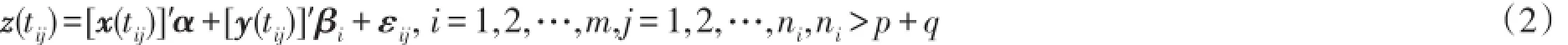
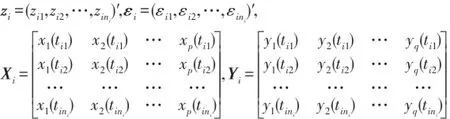
则可得

其中p≥0，q≥0，当p=0时固定系数α不存在，模型化为完全随机的形式见文献［1］；当q=0时，模型化为一般线性模型.这里还要求

再进入记号

（一）高中政治教学偏向应试。高中政治教学为应试服务，教学内容多与考试内容相关，对于学生品格培养的内容讲解过少。对于政治的学习，教师过度要求学生背诵，而对于教学内容没有进行深度的讲解，这与促进学生全面发展相矛盾。

其中Di=YiΣY′i+σ2Ini，则（4）式化为

1　参数向量d的估计

若某个C′iCi或者C′C至少有一个特征值很小，则尽管均为无偏估计.但当模型存在复共线性时，使得均方误差很大，导致估计精度差，稳定性不好，文献［3］给出了混合系数线性模型的岭估计.

当M已知且M＞0时，（5）式可化为

同时文献［2］提出了d参数的一种形式的广义最小二乘估计：

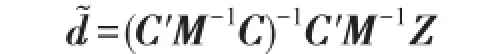
2　h-K型岭估计的提出及基本性质

定义1在模型（5）的基础上，给出参数d的一类新的h-K型岭估计如下：

模型（5）和（7）的参数估计对应的典则形式为

其中Li=CiQi，αi=Q′id，L=CQ，α=Q′d，Q为标准正交特征向量构成的正交阵.则有

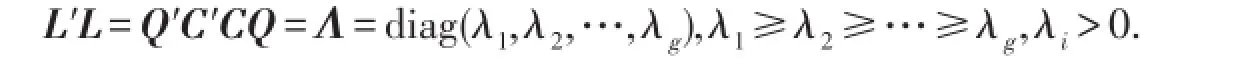
3　应用Stein式压缩技术改进岭估计αˆω（h-K）

这种新型的h-K型岭估计还有其他很好的性质（如在d的线性估计类中可容性等），以下将证明：应用Stein估计回归技术，可寻找h-K型岭估计优于一般h-K型岭估计［3-5］.

定理1在给定h≥1和K＞0的条件下，则存在相应的0＜ω＜1，使得h-K型岭估计）优于，即

证明由（9）式可知

又因

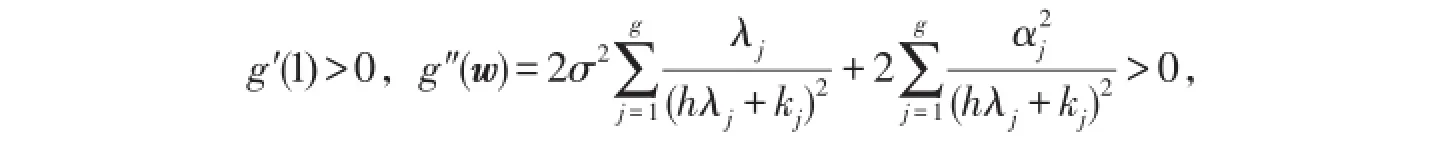
故存在0＜ω＜1时，g（ω）＜g（1），即

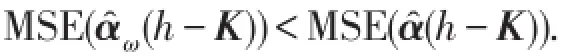
4　参数ω的选择

根据定理1的证明，可得

5　h-K型岭估计的可容许性

引理1［5］对线性回归模型Y=Xβ+e，e～（0，σ2I），假设R（X）=P，则

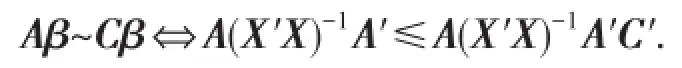
即

6　结论

本文建立在文献［1-2，4，6-8］的基础上，应用Stein式压缩技术基础上，对于变态混合系数线性回归模型的有偏估计提供改进的技术途径.为处理混合系数的经济模型时，达到了对广义岭估计的进一步改进，从而使某些经济现象提供了更加合理的解释.

［1］RAO C R.Linear statistical inference and its applications［J］.New York：Wiley，1093.

［2］庄东辰，茆诗松.混合系数线性模型的参数估计［J］.应用概率统计，1996，12（1）：81-87.

［3］张建军.病态线性回归模型系数的0-c型岭估计［J］.海军工程学院学报，1996（2）：27-34.

［4］潘晋孝，薛亚奎.混合系数线性模型参数的一种新估计［J］.华北工学院学报，1998，19（4）：283-285.

［5］陈静.混合系数线性模型参数的岭估计［J］.青岛大学学报，2007，20（2）：37-41.

［6］RAO C R.The theory of least when the parameter are stochastic and its application to the analysis of grow the curves［J］. Biomitrika，1965，52：447-458.

［7］SWAY P A V B.Statistical inference in random coefficient regression model［M］.New York：Springer-Verlage，1971.

［8］JOHAN S S.A sump totic inference on random coefficient regression model［J］.Scand J Statis，1982，9：201-207.

［9］王志福，范云.线性回归模型系数Stein估计的改进研究［J］.渤海大学学报，2009，30（3）：226-229.

［10］胡桂开.多元线性模型参数的部分压缩［J］.数学理论与应用，2006，26（4）：123-125.

［11］王松桂，贾忠贞.矩阵论中不等式［M］.合肥：安徽教育出版社，1994.

［12］王松桂.线性模型的理论及其应用［M］.合肥：安徽教育出版社，1987.

Research on Improvement of h-K Class Ridge Estimator in Mixed-Effect Coefficient Linear Model

YU Xinhong，WU Jian
（Economy and Technology Institute，Anhui Agricaltural University，230011，Hefei，Anhui，China）

The paper first proposes theh-Kclass of estimators of the coefficients of the mixed-effect linear modelZ（t）=［X（t）］′α+［Y（t）］′βin the ill condition.The ridge estimators is improved by applying the idea of the James-Stein regression on this class of biased estimators under the mean square error criterion；then the condition that the value of the parameter satisfies is given.This class of biased estimators is proved to be ad⁃missible.

mixed-effect linear model；h-Kclass of estimators；Stein estimators；admissibility

O 212.4

A

2095-0691（2016）02-0017-04

2015-11-03

安徽省高校自然科学研究重点项目（KJ2016A246）资助

余新宏（1982-），男，安徽颖上人，硕士生，讲师，研究方向：数理统计.