三区域分片光滑近哈密顿系统的一阶Melnikov函数
檀利军,梁 峰(安徽师范大学 数学计算机科学学院,安徽 芜湖 241003)
教学研究
三区域分片光滑近哈密顿系统的一阶Melnikov函数
檀利军,梁峰①
(安徽师范大学 数学计算机科学学院,安徽 芜湖 241003)
文章给出平面三区域分段光滑近哈密顿系统一阶Melnikov函数一般积分公式,应用该公式研究一个分段光滑的Kukles系统,证明其在某一闭轨附近可分支出两个极限环.
哈密顿系统;极限环;Melnikov函数;分段光滑系统
0 引言
众所周知,一阶Melnikov方法已被广泛用于平面光滑近哈密顿系统的极限环分支,其中包括Hopf分支[1-2]、同宿分支[3-4]和异宿分支[5]等.目前,文献[6]研究两区域分段光滑近哈密顿系统的极限环分支,得到了一阶Melnikov函数一般公式.就我们所知,这种方法已被广泛应用于平面非光滑两区域近哈密顿系统的极限环分支问题的研究,其中包括Hopf分支和同宿分支[7-9]等.本文首先将两区域非光滑近哈密顿系统的一阶Melnikov函数公式推广到三区域.然后,应用该公式研究一个具三区域的分段光滑Kuklus系统的极限环分支问题.
考虑如下的三区域分段光滑近哈密顿系统

其中Hr,Hm,Hl,pr,pm,pl,qr,qm和ql是C∞函数,ε>0是小参数,d∈D⊂Rm是参数,D是有界集.称下面三个系统分别为系统(1)的右子系统、中子系统和左子系统.


以及

对于系统(1)ε=0的未扰系统,作如下假设:
假设1存在一个开区间J=(α,β),使得点A(a,a0(h),A1(a,a1(h),A2(b,a2(h))和A3(b,a3(h)满足Hm(A)=Hm(A3)=h,Hr(A)=Hr(A1),Hm(A1)=Hm(A2),Hl(A2)=Hl(A3),其中h∈J,a0(h)>a1(h),a3(h)>a2(h).

图1 当ε=0时,系统(1)的相图
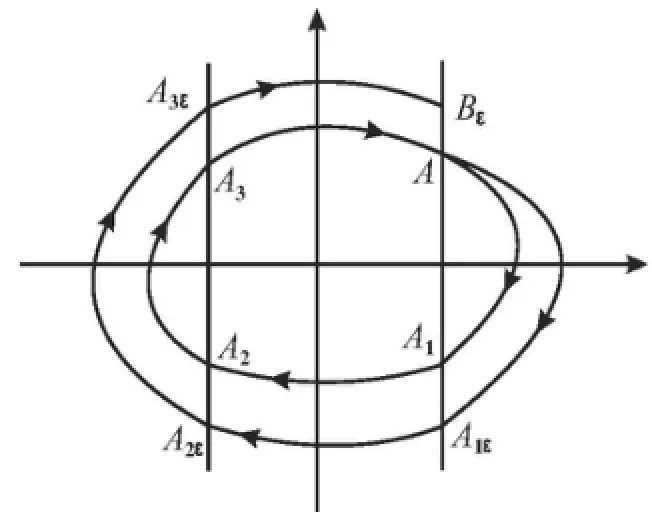
图2 系统(1)始于点A(h)的正半轨
由假设1,2,系统(1)ε=0有一闭轨族如图1所示,当ε充分小时系统(1)从A(h)出发的正半轨依次交l1与l2于点A1ε=(a,a1ε),A2ε=(b,a2ε),A3ε=(b,a3ε)和Bε=(a,bε),如图2所示.同文献[10]中引理3.1.1,可证A1ε,A2ε,A3ε和Bε关于(ε,h)是C∞的,因此,当}ε}充分小时,有

易见,当}ε}充分小,M(h,δ)关于h的孤立零根决定着系统(1)的极限环的个数与分布.称M(h,δ)为系统(1)的一阶Melnikov函数.
1 三区域分片光滑系统一阶Melnikov函数公式
本节给出系统(1)的一阶Melnikov函数的一般公式.
引理1假设1,2成立,则

证明由假设1和2,有
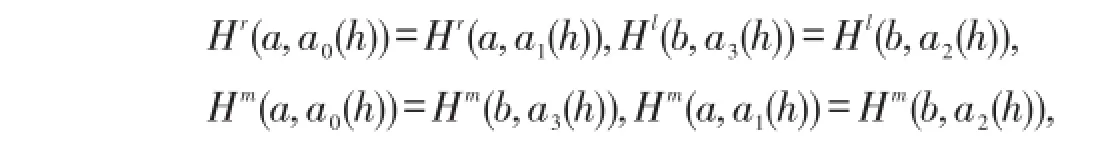
显然,ai(h),i=0,1,2,3是可微的.因此,可以得到
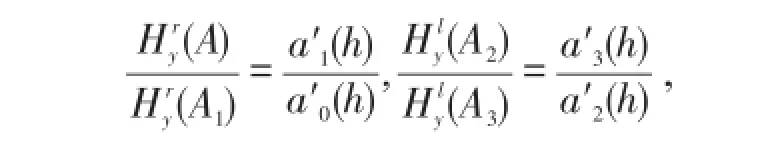
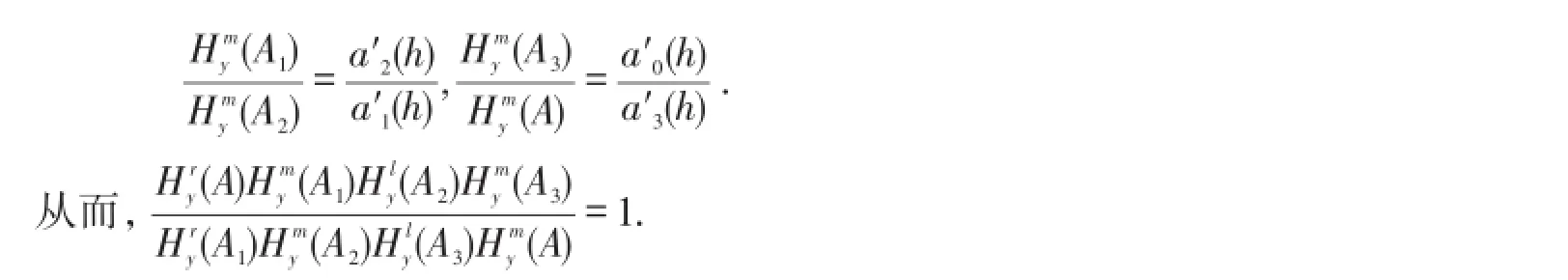
定理1假设1和2都成立,则系统(1)的一阶Melnikov函数公式为
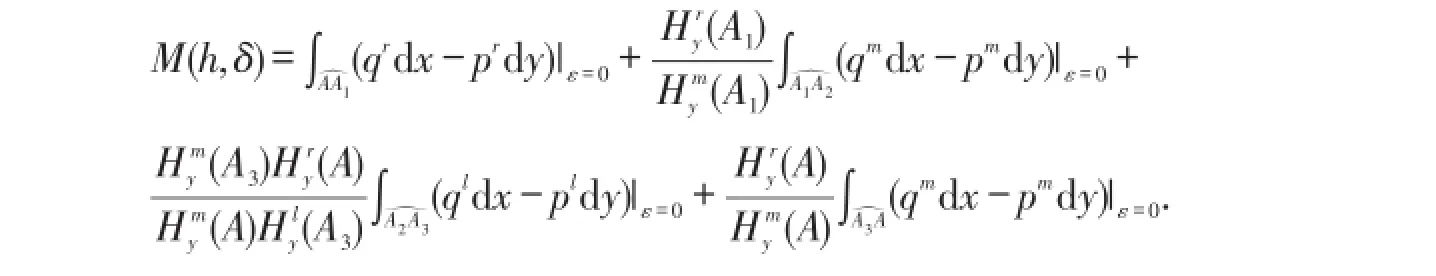
证明令

另一方面,由K8=Hr(A1ε)-Hr(A)和A1ε=A1ε(a,a1ε),有

因此

由K7=Hm(A1ε)-Hr(A1ε)以及(12)式,可得

与(11)式类似,有

同样,由K6=Hm(A2ε)-Hm(A1ε)和A2ε=(b,a2ε),知

因此,再由(12)和(14)式,得到
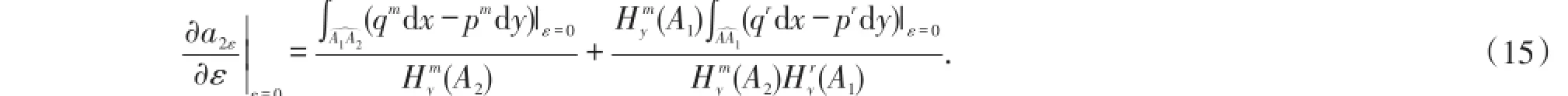
注意到K5=Hl(A2ε)-Hm(A2ε),由(15)式得到

与(11)式类似,有

又由K4=Hl(A3ε)-Hl(A2ε)和A3ε=(b,a3ε),可得
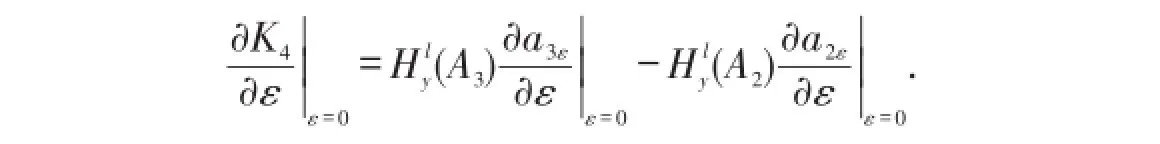
由式(15)和式(17)得
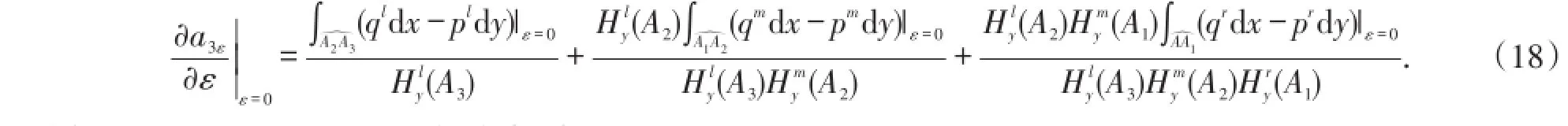
再由K3=Hm(A3ε)-Hl(A3ε)和(18)式,有

此外,同(11)式可得

而由K2=Hm(Bε)-Hm(A3ε)和Bε=(a,bε),知

应用(18),(20)和(21)式,易见

因此,由K1=Hr(Be)-Hm(Bε)和(22)式,有
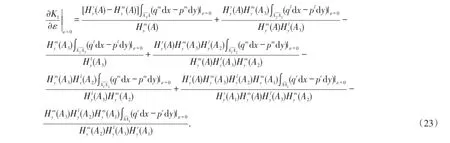
由(8)和(9)式,有

最后,将(11),(13),(14),(16),(17),(19),(20)和(23)式代入上式,并使用引理1,可得
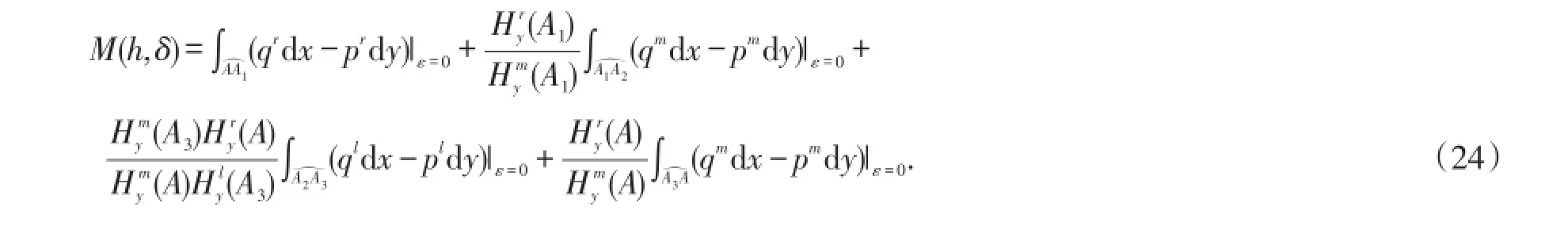
2 一个三区域分段Kukles系统的极限环分支
作为定理1的应用,考虑下面的三区域分段光滑连续Kukles系统

其中,ε>0充分小,w>0是常数,k1,k2和ai(i=0,1,2)是参数,

定理2当ε>0充分小时,系统(25)在L0外侧(或内侧)可分支出2(或1)个极限环.

比较系统(1)和(25),有
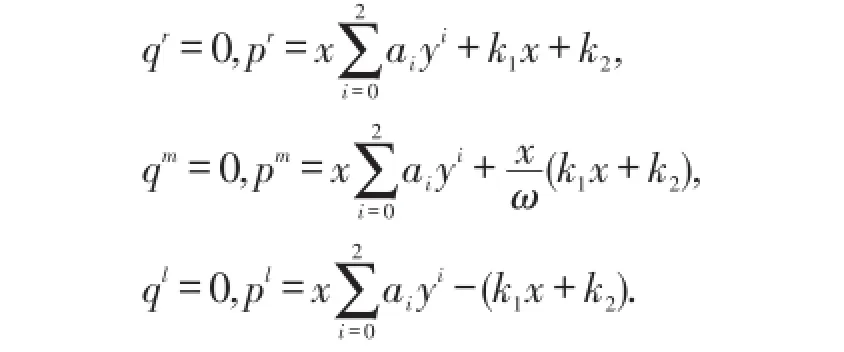
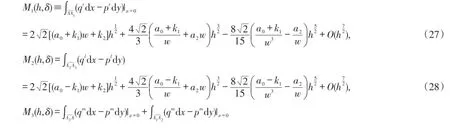

将(27)、(28)和(29)式代入(26)式,则有

为了研究L0内侧的极限环分支,给出系统(25)在0<-h≪1内的一阶Melnikov函数展开式,即有

对于系统(25)在L0外侧的极限环分支,由(30)式有
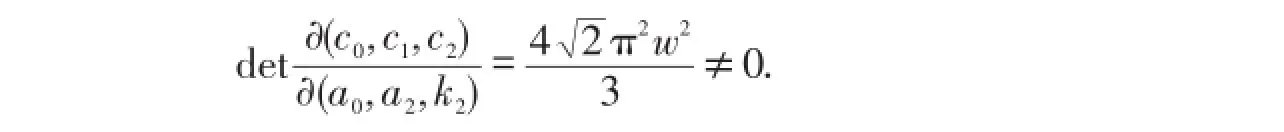
从而,c0,c1,c2可取为自由参数.当0<c0≪-c1≪c2时,由(30)式知,当h>0且充分小时,M(h,δ)关于h可有2个正根.因此,系统(25)在L0的外侧可分支出2个极限环.而对于L0内侧的极限环分支,由于(31)式中b0,b1和b2是线性相关的,且有
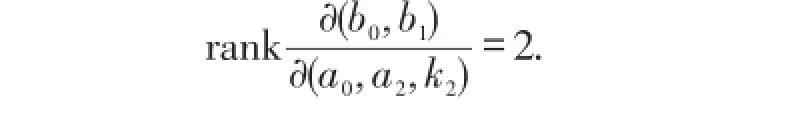
因此,由(31)式知,系统(25)在L0内侧可分支出一个极限环.证毕.
[1]WANG W,HAN M,SUN J.On Hopf cyclicity of a planar systems with multiple parameters[J].Appl Math Lett,2005,18 (6):613-619.
[2]JIANG J,HAN M.Melnikov function and limit cycle bifurcation from a nipotent center[J].Bull des Sci Math,2008,132 (3):182-193.
[3]HAN M,WANG Z,ZANG H.Limit cycle by Hopf and homoclinic bifurcations for near-Hamiltonian systems[J].Chin JContemporary Math,2007,5(5):679-690.
[4]AN Y,HAN M.On the number of limit cycles near a homoclinic loop with a nilpotent singular point[J].J Differential Equations,2015,342(9):3194-3247.
[5]HAN M,YANG J,GAO Y.Limit cycles near homoclinic and heteroclinic loops[J].J Dynam Differential Equations,2008,20(4):923-944.
[6]LIU X,HAN M.Bifurcation of limit cycles by perturbing piecewise Hamiltonian systems[J].Int J Bifurcation and Chaos,2010,5:1-12.
[7]XIONG Y,HAN M.Limit cycle bifurcations in a class of perturbed piecewise smooth systems[J].Appl Math Comput,2014,242:47-64.
[8]LIANG F,HAN M.Limit cycles near generalized homoclinic and double homoclinic loops in piecewise smooth systems[J]. Chaos Soliton Fractrals,2012,45(4):454-464.
[9]LIANG F,HAN M,ROMANOVSKI V G.Bifurcation of limit cycles by perturbing a piecewise linear Hamiltonian system with a homoclinic loop[J].Nonlinear Anal,2011,75(11):4355-4374.
[10]HAN M.Bifurcation theory of limit cycles[M].Beijing:Science Press,2013.
The First Melnikov Function of a Piecewise near-Hamiltonian System with Three Zones
TAN Lijun,LIANG Feng
(Department of Mathematics,Anhui Normal University,241003,Wuhu,Anhui,China)
In this paper,we first give an integral formula of the first order Melnikov function which can be used to study limit cycle bifurcations of piecewise smooth near-Hamiltonian systems with three zones.Then,by using this formula,we consider a piecewise smooth Kukles system with three zones,and prove that 2 limit cycles can be bifurcated near a closed orbit.
Hamiltonian systems;limit cycles;Melnikov function;piecewise smooth system
O 175
A
2095-0691(2016)02-0001-07
2015-12-31
安徽省自然科学基金项目(1308085MA08)
檀利军(1989-),女,安徽池州人,硕士,研究方向:泛函微分方程.通讯作者:梁峰(1974-),男,安徽太和人,博士,副教授,研究方向:微分方程理论及应用.

