基于有限元强度折减法的土质边坡稳定性分析

高姝妹，李晓宁，冯 君（.成都地铁运营有限公司，成都 60000； .西南科技大学，四川 绵阳 6000；.中铁二院工程集团有限责任公司，成都 600）

基于有限元强度折减法的土质边坡稳定性分析

高姝妹1，李晓宁2，冯 君3
（1.成都地铁运营有限公司，成都 610000； 2.西南科技大学，四川 绵阳 621000；3.中铁二院工程集团有限责任公司，成都 610031）

通过求解安全系数的原理，分析土质边坡的稳定性。采用ANSYS有限元分析软件，根据莫尔-库仑六边形外接圆DP屈服准则，基于强度折减原理求解土质边坡的安全系数。该方法通过不断折减安全系数，并不断判断边坡系统的稳定性，当计算不收敛时，可推断该系统正处于稳定至不稳定的临界状态，则该时刻对应的折减系数可判断为该边坡的安全系数。基于此，可以判定土质边坡在不同外部荷载和自重作用下的稳定性。该方法简单易懂，并具有较强的工程实践性。

边坡安全系数；有限元分析方法；强度折减原理；屈服准则

1　引言

近年来随着工程的不断增加，边坡稳定性研究日益重要，日常通常使用的边坡稳定方法主要有塑性极限分析法、极限平衡法等。而日前常用的研究方法都存在一定的弊端，比如以上几种研究方法都是基于极限平衡理论基础上分析土体，假定滑裂面为理想的圆弧状、折线状等，没有考虑到土体结构自身的应力-应变关系，无法队边坡的实际破坏和发展进行过程分析，同时也无法考虑到土体和支档共同作用及其变形协调。

而有限元强度折减法不仅可以针对各种形态复杂的边坡进行计算，模拟出土体与支护共同作用过程，同时可以模拟出土体失稳过程及滑移面总装，求出土体的应力-应变关系，同时可以结合土体的非线性本构关系，使计算结果与现实更为接近。

2　有限元强度折减安全系数定义

通过ansys分析软件，不断降低土质边坡的C、φ值，直至破坏时，C、φ降低倍数w就是安全系数。

对于摩尔-库仑材料，强度折减安全系数可表示为：

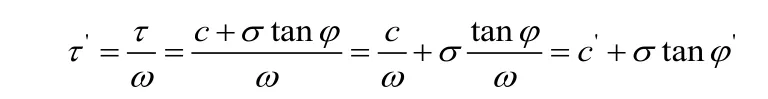
3　基本原理

3.1D-P准则

目前新型的有限元软件为ANSYS，该软件采用的为德鲁克-普拉格准则，即D-P准则，该理论较其他理论更强调了体积应力、剪应力及中间主应力共同作用下对岩石力学强度的影响，也更能反映工程实际情况。

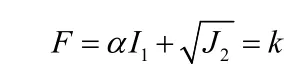
式中I1，J2分别为应力张量的第一不变量和应力偏张量的第二不变量。这是一个通用表达式，通过变换α，k的表达式就可以在有限元中实现不同的屈服准则。α、k是与岩土材料内摩擦角ϕ和粘聚力c有关的常数。

在有限元边坡稳定性分析中采用不同屈服准则也会产生不同的安全系数。①传统极限平衡法：该方法所使用的屈服准为摩尔-库仑破坏准则，该准则在三维应力空间的屈服面存在棱角奇异点而导致数值不收敛。②德鲁克-普拉格准则在π平面上是一个圆，且表述简单，便于数值计算，ANSYS有限元软件采用的屈服准则为摩尔-库仑六边形外接圆DP1准则。实践证明用此准则计算结果偏大。后人经过不断的探讨分析，将不同DP准则进行转化计算，得出了逼近真实安全系数的屈服准则［1］。见图1：

3.2各准则参数换算［2］

图1　各类屈服准则在π平面上的曲线

表1　各准则参数换算

3.3不同DP准则间转化［3］

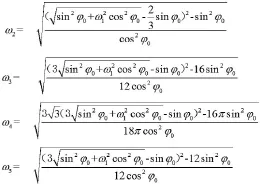
计算原理：将ANSYS中求得的折减系数ω1转化成满足M-C屈服准则的ω2、ω3、ω4或ω5。对于边坡实际中的抗剪强度值，应首先选用折减系数ω1i进行折减计算，同时将折减后的数值带入ANSYS有限元软件中进行计算，经过多次计算，直至边坡平衡达到临界状态值，这次是的ω1i即为德鲁克-普拉格准则下的强度折减系数ω1，最后通过转换公式求出相应安全系数进行比较［4］。

4　案例分析

4.1工程概况

某土质边坡，坡高H=400m，土容重γ=2500KN/m3，弹性模量E=20GPa，粘聚力c=0.9Mpa，内摩擦角ϕ=42.8。，泊松比v=0.43。

4.2模型建立及网格划分

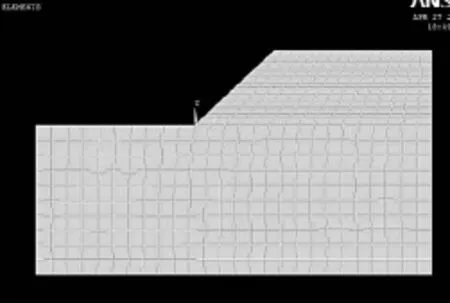
图2　边坡模型

4.3结果分析

图3　折减系数为1时的计算结果

从图3中可以看出计算结果是收敛的，所以边坡未发生破坏。

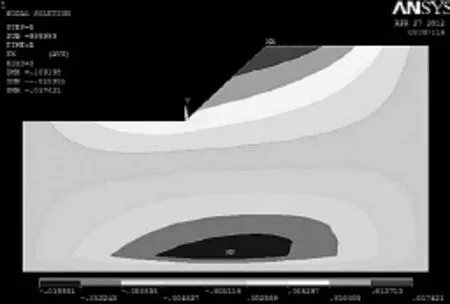
图4　折减系数为2.6时的X方向位移云图

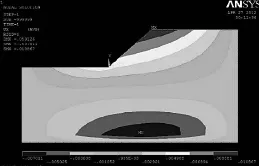
图5　折减系数为2.8时的X方向位移云图

图6　折减系数为2.8时的计算结果

从图4中看以看出折减系数为2.6时水平位移109.198mm，图5中折减系数2.8时水平位移为59.126mm，发生突变，同时折减系数为2.8时计算不收敛（图6），根据破坏准则［5］知安全系数就是2.8。

将DP1得到的2.8带入DP5［6］得W5=2.09，与传统计算得到的2.13误差1.8%，所以该方法可以采用。

5　结论

有限元强度折减法是一个具有广阔发展前景的方法，该法的最大优点是不需要事先确定滑动面的破坏模式，不需要确定滑面的具体形态和位置。

本文中案例计算结果与传统的安全系数相差1.8%左右，说明该方法应用于工程的可行性。案例采用的破坏判据是郑颖人、赵尚毅研究进展里的计算不收敛以及位移突变判据。

此方法在国外70年代就采用，在国内未能推广原因有三：

（1）目前国内有限元处理水平较低，缺乏大规模应用的严密可靠的商用程序；

（2）日前研究中有限元法中的边坡破坏力学机理尚不是很清楚，对于边坡达到极限破坏时的判别依据尚不统一。

（3）有限元强度折减法中具体操作技巧掌握较少，计算得到的安全系数与实际情况的差别较大，可信度不是很高。

随着今年研究的不断深入，以上缺陷都逐一得到解决，比如美国研制的ANSYS，破坏判据有计算不收敛性，特征部位突变性，塑性区贯通性，屈服准则间的转换可以使结果精度提高等等，使得该方法在未来有良好发展前景。在有限元折减系数法中虽然有考虑到多种土层边坡［2］、孔隙水的影响、非自重外荷以及岩质边坡中的节理［7］等的影响，但是仍需要不断深入研究。

［1］赵尚毅，郑颖人，时卫人等.用有限元强度折减法求边坡稳定安全系数［J］.岩土工程学报，2002，24（03）：343-346.

［2］熊欢，肖盛燮.基于Drucker-Prager系列准则的边坡安全系数计算方法［J］.重庆交通大学学报：自然科学版，2012，29（04）：582-586.

［3］陈小念.有限元强度折减法分析土坡稳定性初探［J］.路基工程，2009，5（146）.

［4］张鲁渝，郑颖人，赵尚毅，时卫民.有限元强度折减系数法计算土坡稳定安全系数的精度研究［J］.2003（01）：21-26.

［5］郑颖人，赵尚毅，宋雅坤.有限元强度折减法研究进展［J］.后勤工程学院学报，2005（03）.

［6］杨雪强，凌平平，向胜华.基于系列Drucker-Prager破坏准则评述土坡稳定性［J］.岩土力学，2009，30（04）：865-870.

［7］郑颖人，赵尚毅.有限元强度折减法在土坡与岩坡中的应用［J］.岩石力学与工程学报，2004.23（19）：3381-3388.

10.16640/j.cnki.37-1222/t.2016.14.218