基于分数阶模型的完整非保守系统的Lie对称性与守恒量

张孝彩，张 毅

（1.苏州科技大学 数理学院，江苏 苏州215009；2.苏州科技大学 土木工程学院，江苏 苏州215011）

基于分数阶模型的完整非保守系统的Lie对称性与守恒量

张孝彩1，张 毅2*

（1.苏州科技大学 数理学院，江苏 苏州215009；2.苏州科技大学 土木工程学院，江苏 苏州215011）

研究基于分数阶模型的完整非保守系统的Lie对称性与守恒量。首先，基于分数阶Hamilton原理导出了分数阶d'Alembert-Lagrange原理并建立分数阶Euler-Lagrange方程，研究一般无限小变换下的Lie对称性，建立确定方程，给出分数阶完整非保守系统Lie对称性的定义和判据；其次，给出Lie对称性的分数阶Noether型守恒量存在的条件及形式；最后，举例说明结果的应用。

分数阶模型；非保守系统；Lie对称性；Noether型守恒量

Lie对称性研究的是微分方程在无限小群变换下的不变性。Lutzky［1］于1979年首次将微分方程的Lie理论应用于力学系统的运动微分方程，开始研究动力学系统的Lie对称性与守恒量。赵跃宇［2］于1994年把Lie对称性理论拓展至非保守力学系统。梅凤翔［3］全面系统地研究了约束力学系统的Lie对称性与守恒量。关于Lie对称性与守恒量的研究已经取得了丰硕成果［4-10］。

1996年，Riewe［11］将分数阶微积分应用于非保守系统的动力学建模。此后，Agrawal［12］，Atanackovic［13］，Torres［14］，Luo［15］，Zhang［16-18］等基于分数阶模型开展了力学系统的变分问题及其对称性的研究。但研究主要限于分数阶Noether对称性与守恒量，而分数阶Lie对称性的研究较少。Fu［19-21］等研究了分数阶Hamilton系统和分数阶非完整系统的Lie对称性和守恒量。Song和Zhang［22］研究了分数阶Birkhoff系统的Lie对称性及其摄动理论。笔者将进一步研究分数阶完整非保守系统的Lie对称性与守恒量。

1 分数阶导数的定义和性质

该节介绍文中将涉及到的Riemann-Liouville分数阶导数定义及其有关性质。

设f（t）是区间［a，b］上的连续可积函数，则Riemann-Liouville分数阶左导数定义为

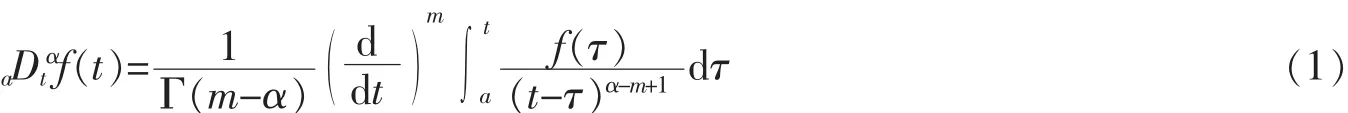
Riemann-Liouville分数阶右导数为

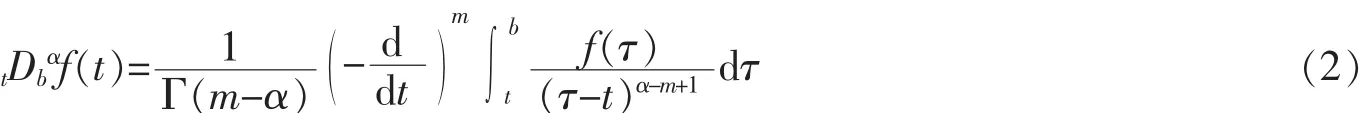
其中Γ（*）是Gamma函数，α是导数的阶，且m-1≤α＜m，m为正整数。如果α是整数，上述定义成为整数阶导数，有

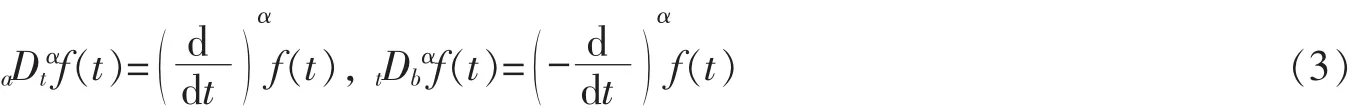
当整数阶导数和分数阶导数复合运算时，有

若f和g是［a，b］上的光滑函数，t∈［a，b］，且成立f（a）=0或g（b）=0，则在Riemann-Liouville分数阶导数下，有关系式［11］

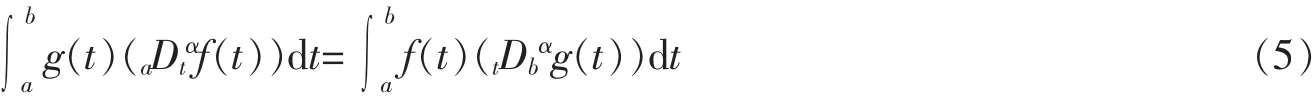
2 分数阶Lie对称性及其Noether型守恒量

2.1 分数阶Euler-Lagrange方程

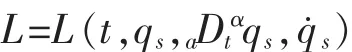
且满足

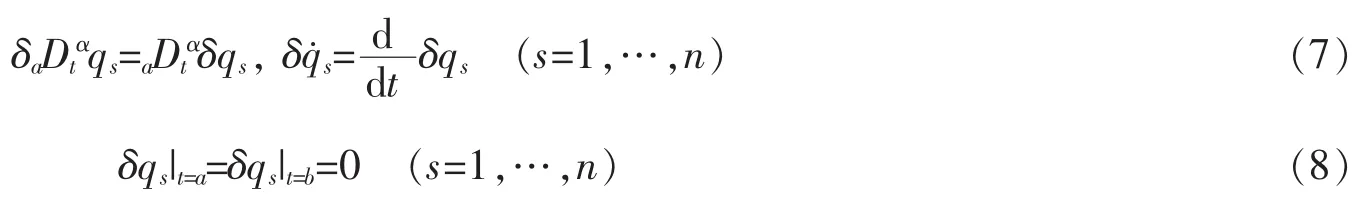
对L求变分，得到

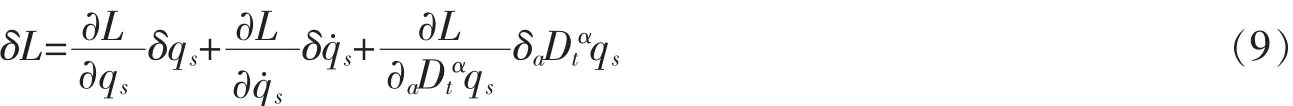
故式（6）可写为

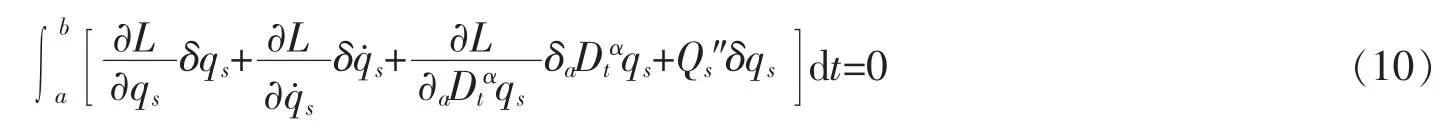
利用式（5）和式（8）得

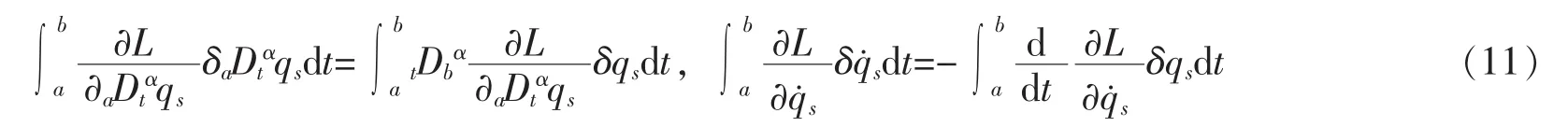
将式（11）代入式（10），有

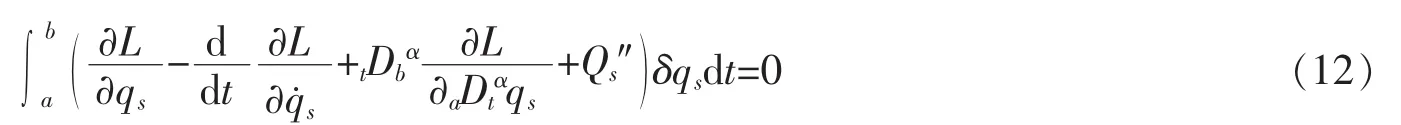
由积分区间［a，b］的任意性，得到

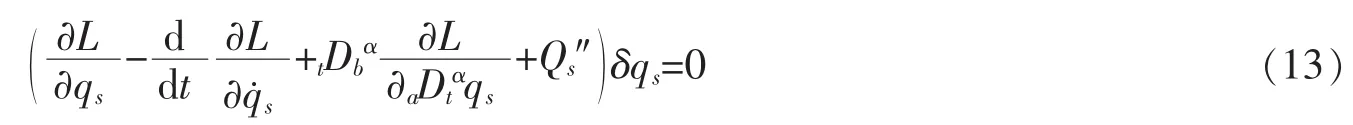
式（13）可称为分数阶的d'Alembert-Lagrange原理。对于完整力学系统，δqs（s=1，…，n）互相独立，于是有

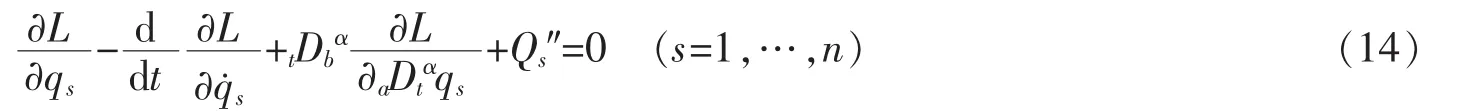
式（14）可称为基于分数阶模型的完整非保守系统的Euler-Lagrange方程。当不存在分数阶导数项时，方程（14）退化为经典的完整非保守系统的运动微分方程。

假设系统非奇异，即设

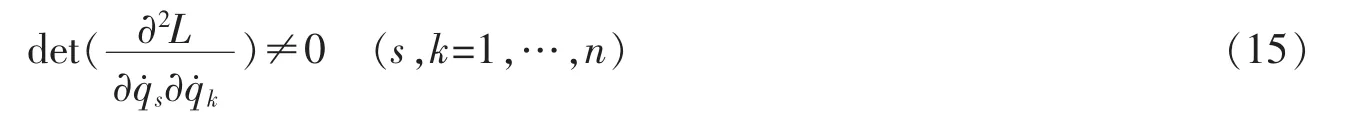
则由式（14）可求出下面的形式

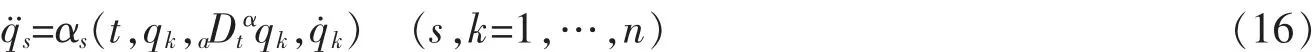
2.2 系统的Lie对称性

引入无限小变换

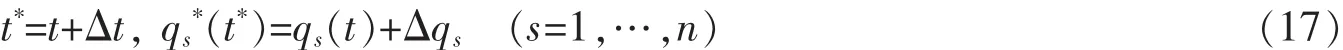
其展开式为

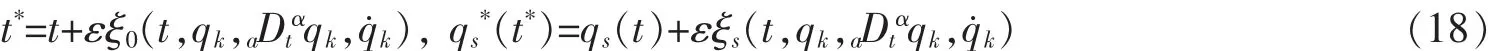
其中ε为小参数，ξ0，ξs称为无限小变换的生成元。

引入无限小生成元向量

其一次扩展为

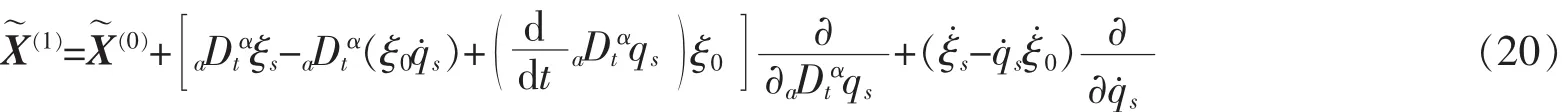
二次扩展为

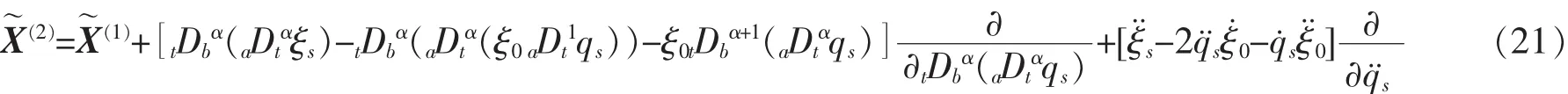
根据微分方程在无限小变换下的不变性理论知，方程（16）在无限小变换（18）下的不变性表为

式（22）等价于如下方程

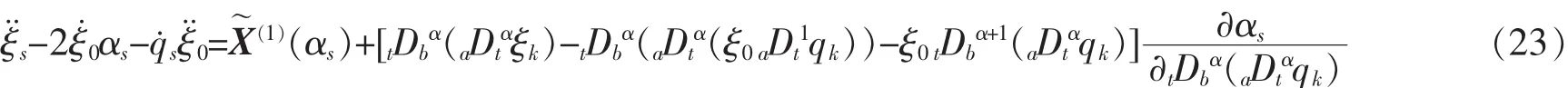
称方程（23）为Lie对称性的确定方程。于是有

定义1 如果无限小变换（18）的生成元ξ0，ξs满足确定方程（23），则相应不变性称为基于分数阶模型的完整非保守系统的Lie对称性。

2.3 Lie对称性导致的Noether型守恒量

Lie对称性不一定导致守恒量。下面的定理给出基于分数阶模型的完整非保守系统（14）的Lie对称性导致Noether型守恒量的条件及其形式。

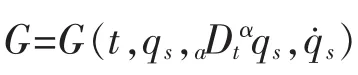
则完整非保守系统（14）的Lie对称性导致如下形式的Noether型守恒量

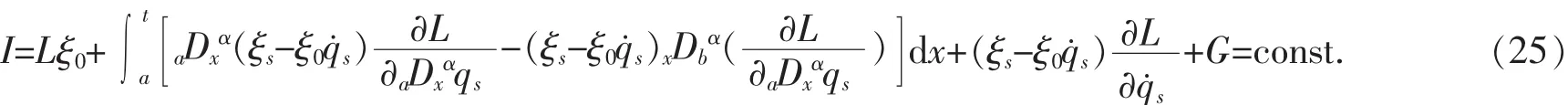
证明 由于

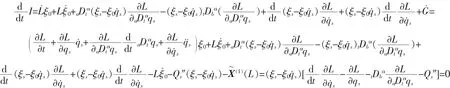
积分之，得到守恒量式（25）。

3 算例

例1 系统的Lagrange函数为

其中r为阻力系数，i为虚数单位，式中两项为动能和线性摩擦力能量［11］。研究系统的Lie对称性和守恒量。

首先，建立系统的运动微分方程。由式（14）得

注意到

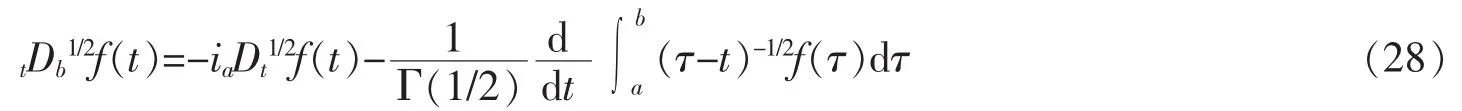
易知

故可得

其次，建立Lie对称性的确定方程，并求解。由式（23）得

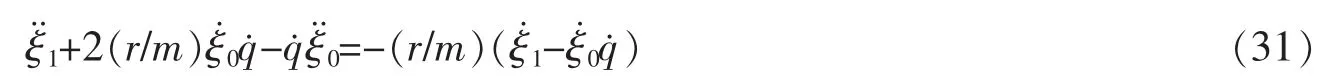
方程（31）的解为

然后，建立结构方程，并求解规范函数。由式（24）得

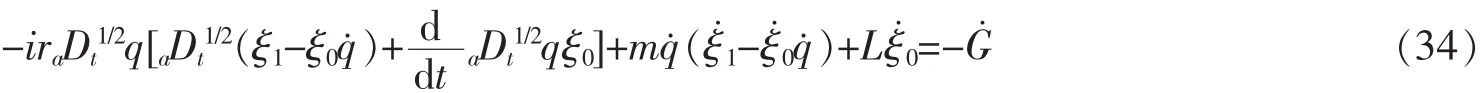
将生成元（32）、（33）代入（34），分别得到

最后，求Lie对称性导致的Noether守恒量。依据定理1，将式（32）、（35）和式（33）、（36）分别代入守恒量式（25），可得

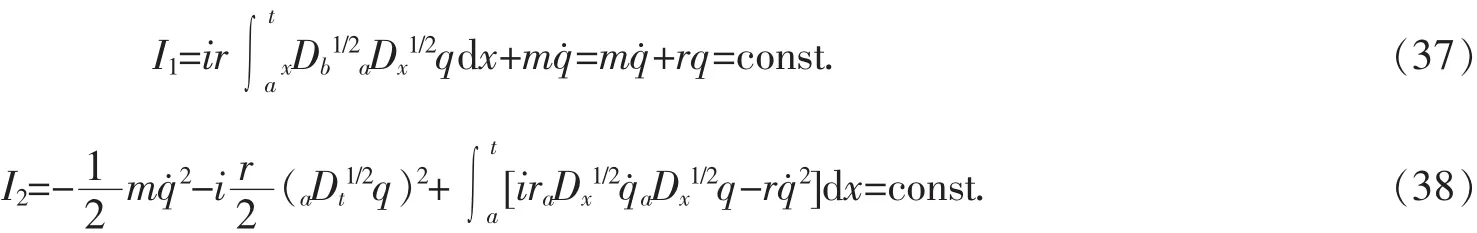
如果系统不含有分数阶项，则式（37）、（38）退化为

例2 力学系统的Lagrange函数和广义力为

其中，质量m和阻尼系数c均为常数。

系统的运动微分方程给出

由确定方程式（23）得

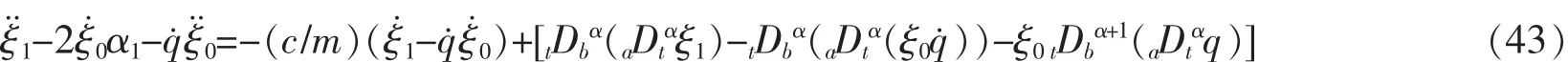
式（43）有解

由结构方程（24）得

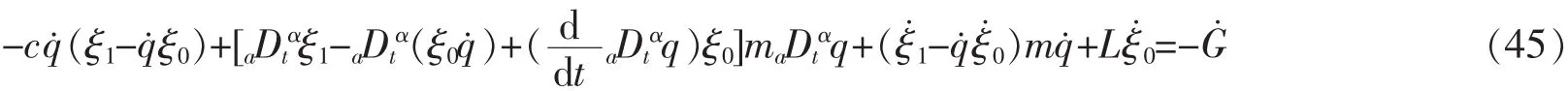
将式（44）代入式（45）得

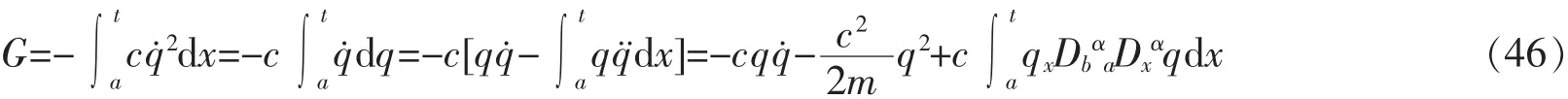
由式（44）和（46），依据定理1，得

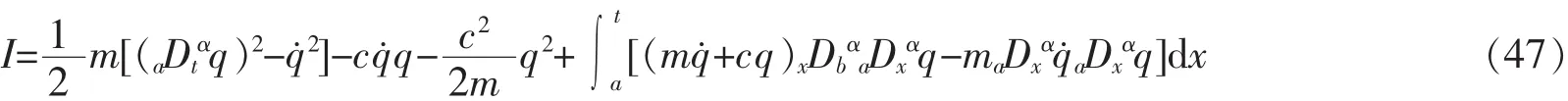
式（47）是由系统的Lie对称性（44）导致的Noether守恒量。如果系统不含有分数阶项，则式（47）给出

这是经典的完整非保守系统Lie对称性导致的Noether守恒量。

4 结语

［1］LUTZKY M.Dynamical symmetries and conserved quantities［J］.Journal of Physics A：Mathematical and General，1979，12（7）：973-981.

［2］赵跃宇.非保守力学系统的Lie对称性和守恒量［J］.力学学报，1994，26（3）：380-384.

［3］梅凤翔.李群和李代数对约束力学系统的应用［M］.北京：科学出版社，1999.

［4］梅凤翔，尚玫.一阶Lagrange系统的Lie对称性与守恒量［J］.物理学报，2000，49（10）：1901-1903.

［5］梅凤翔.包含伺服约束的非完整系统Lie对称性与守恒量［J］.物理学报.2000，49（7）：1207-1210.

［6］张毅，梅凤翔.单面完整约束力学系统的Lie对称性研究［J］.科学通报，2000，45（4）：353-356.

［7］FU J L，CHEN X W，LUO S K.Lie symmetries and conserved quantities of rotational relativistic systems［J］.Applied Mathematics and Mechanics，2000，21（5）：549-556.

［8］ZHANG H B，GU S L.Lie symmetries and conserved quantities of Birkhoff systems with unilateral constraints［J］.Chinese Physics，2002，11（8）：765-770.

［9］LUO S K.New types of the Lie symmetries and conserved quantities for a relativistic Hamilton system［J］.Chinese Physics Letters，2003，20（5）：597-599.

［10］LOU Z M.The Lagrangian and the Lie symmetries of charged particle motion in homogeneous electromagnetic field［J］.Chinese Physics，2006，15（5）：891-894.

［11］RIEWE F.Nonconservative lagrangian and hamiltonian mechanics［J］.Physical Review E，1996，53（2）：1890-1899.

［12］AGRAWAL O P.Formulation of Euler-Lagrange equations for fractional variational problems［J］.Journal of Mathematical Analysis and Applications，2002，272（1）：368-379.

［14］MALINOWSKA A B，TORRES D F M.Fractional Calculus of Variations［M］.Singapore：Imperial College Press，2012.

［15］LUO S K，LI L.Fractional generalized Hamiltonian mechanics and Poisson conservation law in terms of combined Riesz derivatives［J］.Nonlinear Dynamics，2013，73（1/2）：639-647.

［16］ZHANG Y，ZHOU Y.Symmetries and conserved quantities for fractional action-like Pfaffian variational problems［J］.Nonlinear Dynamics，2013，73（1/2）：783-793.

［17］LONG Z X，ZHANG Y.Noether's theorem for fractional variational problem from El-Nabulsi extended exponentially fractional integral in phase space［J］.Acta Mechanica，2014，225（1）：77-90.

［18］ZHANG Y，ZHAI X H.Noether symmetries and conserved quantities for fractional Birkhoffian systems［J］.Nonlinear Dynamics，2015，81（1/2）：469-480.

［19］周莎.分数阶约束力学系统的Noether对称性和Lie对称性理论研究［D］.杭州：浙江理工大学，2012.

［20］ZHOU S，FU H，FU J L.Symmetry theories of Hamiltonian systems with fractional derivatives［J］.Science China Physics，Mechanics and Astronomy，2011，54（10）：1847-1853.

［21］SUN Y，CHEN B Y，FU J L.Lie symmetry theorem of fractional nonholonomic systems［J］.Chinese Physics B，2014，23（11）：110201.

［22］SONG C J，ZHANG Y.Conserved quantities and qdiabatic invariants for El-Nabulsi's fractional Birkhoff system［J］.International Journal of Theoretical Physics，2015，DOI 10.1007/s10773-014-2475-0.

［23］梅凤翔.分析力学（下卷）［M］.北京：北京理工大学出版社，2013.

责任编辑：谢金春

The Lie symmetry and conserved quantity for holonomic non-conservative systems based on fractional models

ZHANG Xiaocai1，ZHANG Yi2
（1.School of Mathematics and Physics，SUST，Suzhou 215009，China；2.School of Civil Engineering，SUST，Suzhou 215011，China）

In this paper，we studied the Lie symmetry and conserved quantity for holonomic non-conservative systems based on fractional models.Firstly，we deduced the fractional principle of d'Alembert-Lagrange from the fractional Hamilton principle and established the fractional Euler-Lagrange equations.The Lie symmetry under the general infinitesimal transformations was investigated and its determination equations were established.Moreover，the definition and criterion of the Lie symmetry for the fractional holonomic non-conservative systems were given.Secondly，we provided the existence condition and the form of the Noether conserved quantity deduced from the Lie symmetry.Lastly，two examples were given to illustrate the application of the results.

fractional models；non-conservative systems；Lie symmetry；Noether conserved quantity

O316 MR（2000）Subject Classification：70H33；70F25

A

1672-0687（2016）02-0008-06

2015-07-06

国家自然科学基金资助项目（11272227）；江苏省普通高校研究生科研创新计划项目（KYZZ_0350）；苏州科技学院研究生科研创新计划项目（SKCX14_058）

张孝彩（1988-），女，河南驻马店人，硕士研究生，研究方向：力学中的数学方法。*通信联系人：张 毅（1964-），男，博士，教授，博士生导师，E-mail：zhy@mail.usts.edu.cn。