基于准实时数据的智能配电网状态估计
李 滨 杜孟远 祝 云 韦 化
(广西大学广西电力系统最优化与节能技术重点实验室 南宁 530004)
基于准实时数据的智能配电网状态估计
李滨杜孟远祝云韦化
(广西大学广西电力系统最优化与节能技术重点实验室南宁530004)
针对配电网首端量测准确度较高,而其余位置量测冗余度较低甚至没有量测量的特点,提出一种新的配电网DMS系统架构和适用于智能配电网的状态估计方法,利用准实时数据构造目标函数,依据历史记录设置不等式约束。与传统配电网方法不同,该方法可用于准实时量测在线率较低的配电网。因其是最优潮流意义下的状态估计,可以利用内点法求解。采用某市9节点配电网线路作为算例进行仿真,并对结果进行了详细讨论,同时以广泛使用的33节点配电网算例进一步验证。结果表明,所提方法计算速度快、收敛性好,可以实现智能配电网在线状态估计。该方法对于准实时量测在线率低的配电线路也有理想的估计效果,能较好地获得真实值,对线路电流的估计结果满足智能配电网高级应用的需求。
状态估计智能配电网数据挖掘内点法
0 引言
智能配电网通过多种先进信息技术,实现了电网的数字化、信息化、自动化和智能化[1-5]。为了对配电网进行控制和优化,实现与用户的互动,需要利用自动化手段采集大量配电网测量数据以完成各种计算和分析功能。
随着国内重输轻配的观念逐渐改变,很多地区都投入资金进行配电网自动化的改造。发达地区配电网中安装大量测量装置,基本实现了配电网的全面可观性。在经济欠发达地区,如果按输电网的要求安装大量量测装置,供电企业将不堪重负。因此,需要在原理上另辟蹊径。一种解决思路是依据部分缺失的配电网量测信息和配电网内在电关联,利用状态估计方法得出其他“暗箱”信息,以实现配电网运行状态全面观测,为高级应用提供数据基础。对此,许多研究学者展开了智能配电网状态估计的研究,并取得了初步进展。
目前很多国家和地区都在推进智能电网的建设,为了满足更高的配电网安全运行要求,需要从数据源上进行改进,寻求高准确度状态估计方法。高级测量装置开始在一些智能配电网中大量安装,采集的实时数据可以直接提供给状态估计程序[6]。若没有足够的实时数据,则需要提供一定量的伪量测量使状态估计能进行下去。利用历史负荷数据训练神经网络可以得到负荷的伪量测量,伪量测量的方差可以用高斯混合模型得到[7]。由于神经网络的训练是离线进行,并不会对状态估计的实时性造成影响。不良数据会对状态估计的结果造成不利影响。文献[8]利用决策树对不良数据进行分类,依据量测违反配电网测量规律的程度计算相应的质量标签,作为输入数据进行状态估计,避免了传统方法残差淹没的问题。
智能配电网的进步对状态估计提出了新的挑战,需要从模型上着手创造新的方法,适应新形势下的发展。文献[9]利用机器学习等技术组成闭环系统,得到具有抗差性能力的智能配电网状态估计方法,同时适用于不可观与全面可观的配电网。在更智能的配电网中,主要的节点上甚至如主网一样装用矢量测量单元,因而能将相角测量加入智能配电网状态估计方法中,提高估计准确度[10]。以往简化的刀开关、分段开关等元件也应看作节点进行建模,此外配电网合环运行也逐渐成为趋势。为了应对这些新形势,文献[11]提出了基于拓展节点分析(MANA)的智能配电网估计方法。该方法不但十分容易引入新型元件的表达式,也能很好地处理合环网络。文献[12]对智能配电网中元件不同绕组接线方式下的等效模型进行了研究,并应用到三相不平衡状态估计中。配电网中零注入节点的信息可以作为量测量加入到配电网状态估计中,增加量测冗余度。目前常用方法是引入等式约束,使零注入节点的注入功率严格限制为零[13,14]。加快求解速度也是智能配电网状态估计的一个研究方向。文献[14]通过引入支路功率和支路电流作为状态量,直接给出了电压量测量的表达式,量测方程简单,求解容易,收敛快。此外也可用复数形式得到线性化的状态估计方法,状态估计有直接解,计算量少,也避免了r/x比值过大导致的不收敛问题[10]。
目前智能配电网的建设尚处于起步阶段,量测量测量比较少,当前最紧迫的工作是使完全不可监测的配电网实现基本可观,这时容许一定的误差存在。对于配电网而言,合理误差范围内的估计结果是可以接受的。线路始端节点注入功率与网架之间隐含着配电网各节点状态量的联系,已有文献缺少对这方面的研究。实际上利用好这个联系相当于增加了提供给状态估计的信息,有助于提高状态估计的准确度。本文尝试将这个联系用于状态估计中。
针对智能配电网发展过程中存在的问题和特点,本文提出一种新的智能配电网的状态估计方法,在传统状态估计的基础上引入网络潮流方程作为等式约束,并结合历史数据等信息设置不等式约束。通过将模型构造成最优潮流模型的形式,降低了对在线可用准实时量测量数量的要求,准确度则由量测量质量决定。即使所有负荷节点都没有在线可用的准实时量测量,状态估计的结果准确度仍在可接受范围内。本文以功率量测量为主的配电网作为研究对象,经过简单修改也可将电流量测包含在内。该方法计算速度快,可以用于配电网在线状态估计。本文方法适用于处于智能配电网建设初期,测量设备没有全部到位或实用化率不高的阶段。对状态估计准确度没有特别严格的要求时,采用本文方法也可实现向智能配电网平稳过渡。
1 智能配网管理系统
为了对配电网进行监测与控制,典型的智能配电网需要在线路上安装大量电流、电压和功率等量测终端,各区域无测量盲区。数据采集后上传至采集服务器并存储在数据库中,其基本原理如图1所示。由于状态估计依赖数据库中的数据,对采集的数据有较高要求。通常典型的智能配电网采集的数据准确度较高,数据采集与传输时间短,有较高的实时性。

图1 典型智能配电网DMS系统Fig.1 Smart distribution network DMS system
目前国内智能配电网还处于发展阶段,量测装置还不多,其典型量测配置如图2所示。变电站内可以测量线路始端电压和功率,量测装置有较高准确度,与配网线路上其他量测量相比可以作为真实值使用。通常线路部分节点处会安装量测装置上传负荷数据,另一些节点的负荷需要人为到现场拷录,此外很少安装线路电流量测装置。受配电网量测装置同步性的影响,标记为同一时刻的数据,可能是不同时刻的采集值,并不是实时数据,只能称为准实时数据。测量装置的间歇性故障会造成数据无法上传,即无在线可用的准实时量测,造成一定的监测盲区,无法满足智能电网的要求。典型智能配电网DMS(Distribution Management System)系统对量测数据有较高要求,但在图2所示的量测配置下,同一时间断面无法获得足够多在线可用的准实时量测量,以至于只利用这些数据无法进行状态估计。

图2 当前配电网典型量测配置Fig.2 Current typical distribution network measurement configuration
鉴于国内配电网现状,本文提出一种新的DMS系统,充分利用已有的硬件资源,突破了准实时量测在线率低的配网中无法进行状态估计的局限。在此基础上,状态估计可以从不同数据源获得更多的信息来弥补量测不足,在几乎不新增设备的前提下提升对配电网运行状态的观测能力。其基本架构如图3所示。与图1显著的区别在于状态估计被提到DMS数据库之前,成为基础应用,并引入数据挖掘技术。

图3 新的配电网DMS系统Fig.3 Novel distribution network DMS
利用数据挖掘技术能够从供电公司已有系统中得到大量信息。负荷通常分为工业、商业、居民3个类型。支持向量机(Support Vector Machine)算法[15]可以依据给出的负荷特征将负荷分类并归属到这3个类型中,或者利用k平均值(k-Means)[15]在不事先给出特征信息的情况下自动将负荷进行归类,其优点是减少了人为因素影响,能获得数量更多的分类,同时也能将不属于以上3类的负荷归属到相应的类中,实现更准确的负荷分类。对于有准实时数据的负荷,用历史数据最近几天的平均值作为负荷曲线。对于没有准实时数据的负荷,依据分类信息,用同类别其他负荷的曲线代替其负荷曲线。此外,神经网络(Artificial Neural Network)[16]可以接受高维信息,输出每个节点的短期负荷预测,代替负荷曲线使用。
2 智能配电网状态估计模型
量测量可表示为

状态估计的目标函数多采用最小二乘法,其基本形式为

式中,W为测量方差,与量测设备精度有关,W=
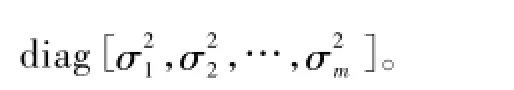
加权最小二乘法是一种无偏估计,求解方法多,收敛性好,是较好的状态估计方法[17],但用于配电网仍然存在问题:通常状态估计的结果不满足潮流方程约束,用估计结果进行潮流计算后始端节点功率与测量值往往不一致。由之前的论述已知,始端点功率可以作为真实值使用,状态估计的结果应该与始端点功率测量值完全一致。此外配电网中准实时量测量冗余度较低,为了提高状态估计的准确度,必须从其他信息源合理地补充一些信息。
基于以上问题,本文提出以下配电网状态估计模型


为了计算方便,选用以下变量作为状态量

式中,α为电压相角,α∈Rs-1。选择量测函数为
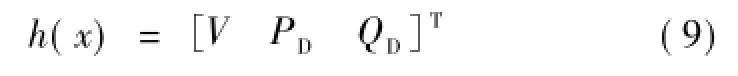
类似的,选取量测量为
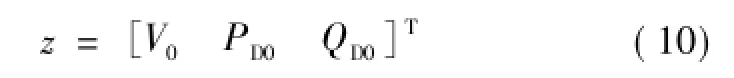
式中,V0、PD0和QD0分别为电压幅值、负荷有功和负荷无功准实时测量值。
式(5)~式(7)给出有两个作用:①给出优化问题的可行域。通过给出一个较小的可行域,减少了最优问题的寻优空间,有利于方法迅速收敛。同时也促使寻优结果向真实值靠近。特别在没有在线可用的准实时测量值时,该约束起到了提供量测冗余的作用;②限制不良数据对估计结果的影响。当存在不良数据时,某些估计值可能与实际值有较大偏差,并可能影响另一些估计值,造成估计质量下降。加入不等式约束后,当估计值偏离实际值时,会被限制在不等式上下界,降低对总体估计的影响。
配电网调度自动化系统除了上传量测量,还会实时上传开关状态等遥信量。遥信量可信度高,相比量测量而言为精确量。如果出现切负荷等操作,式(5)~式(7)中相应的约束也需要进行校正,使负荷约束符合实际情况。
式(6)、式(7)的上下界可以用典型负荷曲线确定。例如图4中实线为典型负荷曲线,实际负荷曲线位于灰色部分内部。如果没有典型负荷曲线,可以采用其他方法确定不等式上下界,一种比简单的方法是利用变压器容量对其进行设置。

图4 负荷曲线示意图Fig.4 Load profile demonstration
与传统状态估计的零注入约束不同,等式约束(4)表示的是配网交流潮流方程,有3个重要的作用:
1)增加可观性。各节点状态量之间隐含电气量之间的联系,可以由一些量推算出另一些量,但某些情况下难以用显示的方法利用这些联系。通过潮流方程将这些联系包含到状态估计过程中,只要能找到一个可行解就必然能获得每个节点上的所有状态量。估计值准确度的高低由量测量的数量等因素决定。
2)潮流方程对配网潮流进行了平衡,强制始端节点功率估计值与量测值一致。头节点量测量可信度很高,最能代表配网运行状态,这样处理使得估计结果尽量与实际运行情况相符,也避免了状态估计结果头节点功率计算结果与量测量不一致的问题。
3)结合网架结构,将始端点注入功率与配电网实际运行状态联系起来。当网架确定后,在特定的始端节点注入功率下,配网内潮流的流向是符合一定规律的。潮流不存在的一些配电网状态自然不会由本文方法得到。虽然存在潮流多解的问题,但在不等式约束下各解之间的偏差会被限制在一定范围内。准实时量测量相当于一个参考,引导估计结果尽量向配电网实际运行状态靠近。这几个因素相互作用都有利于提高状态估计的准确度。
式(3)~式(10)描述的是一个最优化问题,特别是非线性等式约束(4)的非凸性给模型求解带来很大困难。式(4)是交流网络潮流,式(5)~式(7)类似于优化问题中的安全运行约束,整个模型在结构上与最优潮流相近,可以看作一种基于最优潮流的状态估计模型。当前有许多算法可以求解最优潮流模型,为了提高求解速度和获得良好的收敛性,考虑用求解大规模最优潮流比较有效的内点法进行求解[18]。
本文研究以功率量测为主的配电网,一些配电网往往还有电流量测,实际上只需将电流量用其他状态量表示,然后作为等式约束添加到模型中就可以包含电流量测。此时在目标函数中添加相应的电流状态量,量测方差可以依据量测误差传递规律得到[19]。
3 算例介绍与仿真
3.1算例介绍
为了对本文状态估计的性能进行评估,现以一条9节点实际配电线路为例进行测试。线路接线结构绘制于图5中,有两条送电支路。线路参数与负荷列于附表1、附表2中。本文后面还将用一33节点配网系统进一步验证[20]。

图5 9节点配网系统接线图Fig.5 Diagram of the 9-node network
9节点系统算例中所有数据均为标幺值。功率基准值为1 MV·A,电压基准值为10.5 kV。仿真时以潮流计算结果作为真实值,准实时测量值为
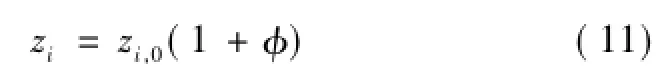
式中,i为单个量测量的序号;zi为准实时测量值;zi,0为潮流计算的真实值;φ是服从正态分布且平均值为零、标准差为σ的随机数。
3.2仿真说明
旧城区配电线路上的负荷增长很慢甚至没有增长,可以用负荷曲线近似代表实际负荷。新建配电线路上负荷增长快,新变压器投入使用后也缺少足够的历史数据形成负荷曲线,难以用典型负荷曲线代表实际负荷。此时不宜用典型负荷曲线确定式(6)、式(7)的上下界,但可以利用变压器容量作为上界。例如一台100 kV·A的变压器,设置相应PD的上界为100 kW,QD的上界为100 kvar。
此外配电网中的量测配置也会对状态估计的结果造成很大影响。理想的情况是变压器均有功能正常的量测终端,每隔一段时间上传准实时数据。实际情况中由于数据链路中断或掉包等原因,会造成部分区域量测量的缺失。
由于冗余度较低,配电网状态估计主要以负荷节点的功率、电压量测量作为数据来源。结合之前的描述,现对6种情形进行状态估计的仿真。所有情形中量测数据中没有错误数据,量测终端的准确度相同,始端节点功率作为真实值加入潮流方程中。每种情形满足的不同条件列于表1中。

表1 9节点系统6种情形仿真条件Tab.1 Simulation conditions of 6 scenarios for 9 node network
3.3仿真参数选择
电压波动按-7%~7%考虑,即电压幅值V上下限分别为0.93和1.07。
以潮流计算结果作为真实值,按式(11)取σ为0.03叠加误差形成量测量。为了考虑实际应用中不能准确确定负荷范围的情况,在负荷功率真实值上乘以[0.8,1.2]范围内的随机数作为负荷曲线的值,然后在此基础上浮动 ±20%作为负荷不等式上下界。
3.4仿真结果讨论
6种情形下状态量估计结果与它们的真实值、准实时量测量的值如图6~图9所示。虽然一些情形中的节点没有准实时量测值,为了进行对比,仍将所有准实时量测量列出来。
由图6~图9可见,A1情形中,某些节点负荷有功、无功的估计值与准实时量测值较接近。A1中节点上只有功率和电压的准实时量测量,除非有其他假设条件,否则可以认为这两个量是相互独立的。由于缺少量测冗余,某些节点的估计结果会向准实时量测量的值靠近。
在A2情形中,由于在线可用准实时量测量较少,状态量的估计值与实际值有一定的偏差,但较大的偏差也只出现在个别负荷上。其中由于节点5、6处没有在线可用准实时量测量,状态估计没有可依赖的数据。5号节点的负荷估计值偏大,为了满足功率平衡,6号节点负荷的估计值就会偏小。

图6 9节点系统有功负荷估计值比较Fig.6 Comparison of active load estimation for 9-node network
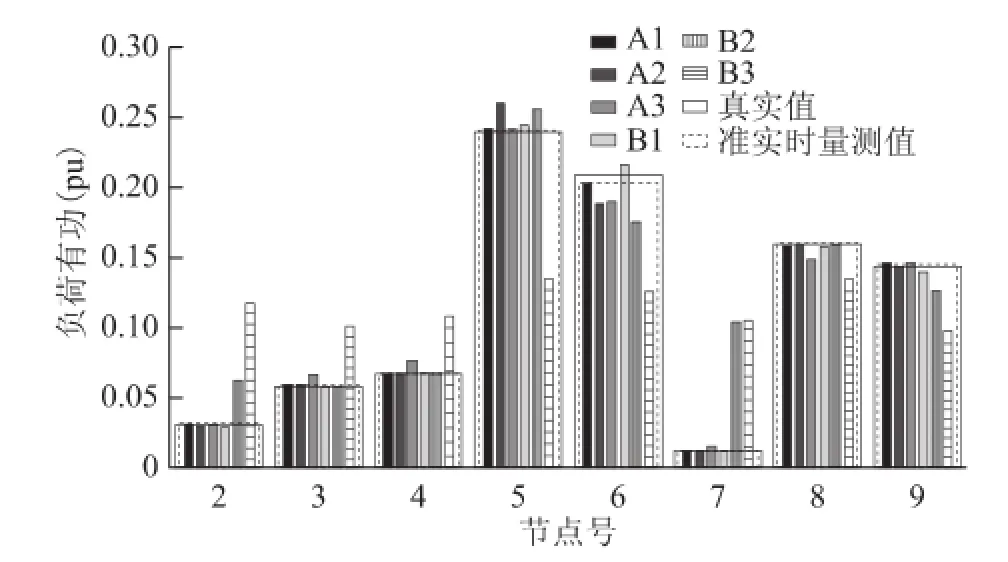
图7 9节点系统无功负荷估计值比较Fig.7 Comparison of reactive load estimation for 9-node network

图8 9节点系统电压估计值比较Fig.8 Comparison of voltage estimation for 9-node network
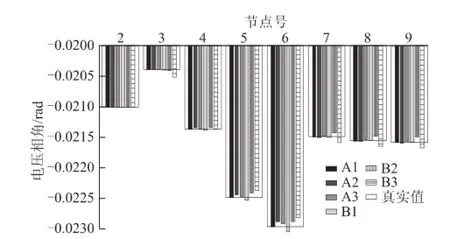
图9 9节点系统相角估计值比较Fig.9 Comparison of angle estimation for 9-node network
在A3情形中,因为没有负荷功率和电压的在线可用准实时量测量,此时估计结果的准确度依赖于不等式上下界。目标函数恒等于零,没有可以依赖的寻优方向,得到的解倾向落于不等式上下界正中间的位置。由于考虑了不能准确确定负荷范围的情况,不等式上下界的中间位置可能离实际值较远,所以估计的准确度与A1、A2比并不理想。然而估计结果仍然会在始端节点功率和网架参数的影响下趋向配电网实际运行状态。同样为了保持功率平衡,某些节点负荷功率估计值偏大,另一些偏小。
B1情形下负荷的估计值仍与量测值较一致。
在B2情形下由于2、5、6、9节点处没有准实时量测量,估计值与真实值有一定的偏差,特别在2号节点处有功和无功的偏差比较大。通过分析发现2号节点处变压器的容量为630 kV·A,但实际有功负荷为85.15 kW,无功负荷为31.28 kvar,换算成视在功率为90.72 kV·A,只有变压器容量的14.39%,属于十分轻载。2号节点处负荷处没有量测值,这一点不等式的上界与实际负荷相比大很多,估计值有一个比较大的取值范围。5、6、9号节点的负荷有功的估计值比真实值小,在满足功率平衡的条件下,2号节点有较大的估计值。2号节点无功负荷估计值偏大的原因类似,在此不赘述。7号节点也属于十分轻载的情况,但在7号节点处有准实时量测量,因而估计值的结果与真实值相差不大。
B3情形下的估计结果最差,在2、7号节点处的有功负荷估计值远大于真实值。2、3、4、7号节点处无功负荷远大于真实值,5、6、8、9处无功负荷又远小于真实值。出现这种偏差的原因与B2情形类似。
由于有线路始端节点功率做支撑,而且有潮流约束,6种情形下电压幅值估计值与真实值基本一致。这是因为加入了潮流约束后,用始端节点功率作为真实值的估计结果更符合配电网实际运行情况。通过潮流约束,各节点的负荷准实时量测量成为了节点电压的量测冗余,有利于提高电压幅值的估计准确度。在A3和B3中电压幅值的估计值也有较高准确度,说明始端节点功率对于状态估计有很重要的作用。
为了表示不同情形之间估计结果的差异,利用

计算图6~图9中估计值与真实值的统计误差。式中,si为真实值;hi(x)为量测函数;为估计的状态量;m为量测量个数。负荷、电压真实值统计误差见表2。
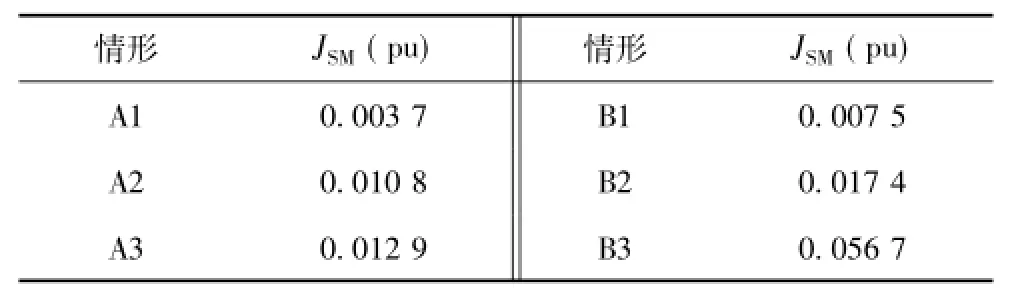
表2 9节点系统6种情形负荷、电压真实值统计误差Tab.2 Real value statistical error of 6 scenarios of 9-node network
类似的可以用

计算图6~图8中估计值与准实时测量值的统计误差,其结果见表3。
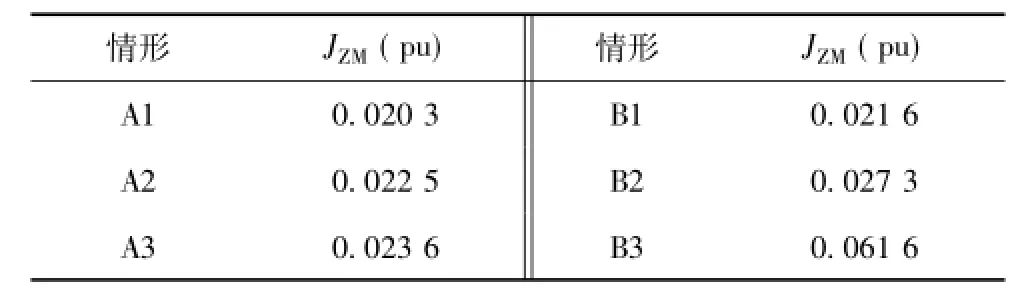
表3 9节点系统6种情形负荷、电压量测值统计误差Tab.3 Measurement value statistical error of 6 scenarios of 9-node network
由表2和表3中数据纵向比较可以看出,A1、A2、A3的JSM都比较小,JZM的值稍大,即估计值与真实值较接近。虽然某些节点负荷估计值会向准实时量测量接近,但总体看来所有状态量估计值仍与实际更接近一些。
在以变压器容量作上下界的情形中,只有B1的JSM统计误差较小,B2和B3的估计结果还是有一定的偏差。同样,B1、B2、B3的JZM大于JSM。以上分析说明本文提出的状态估计一定程度上较好地从量测量中还原出了真实值。
由表2中数据横向比较可以看出,除了A1和B1基本一致外,A2、A3的JSM分别比B2、B3的小,这说明负荷上下界的选取十分重要。一旦不等式上界设得比实际值大很多,估计值也会与真实值偏差大。
在配电网每条支路上安装测量元件是不经济的。利用状态估计可以得到节点的电压和相角,进而计算流过的电流。利用

计算电流估计值与真实值的偏差,式中,ci为用状态量计算的电流值。同样利用式(12)计算估计值与真实值的统计偏差,结果列于表4和表5中,表中*表示每条支路首端线路。
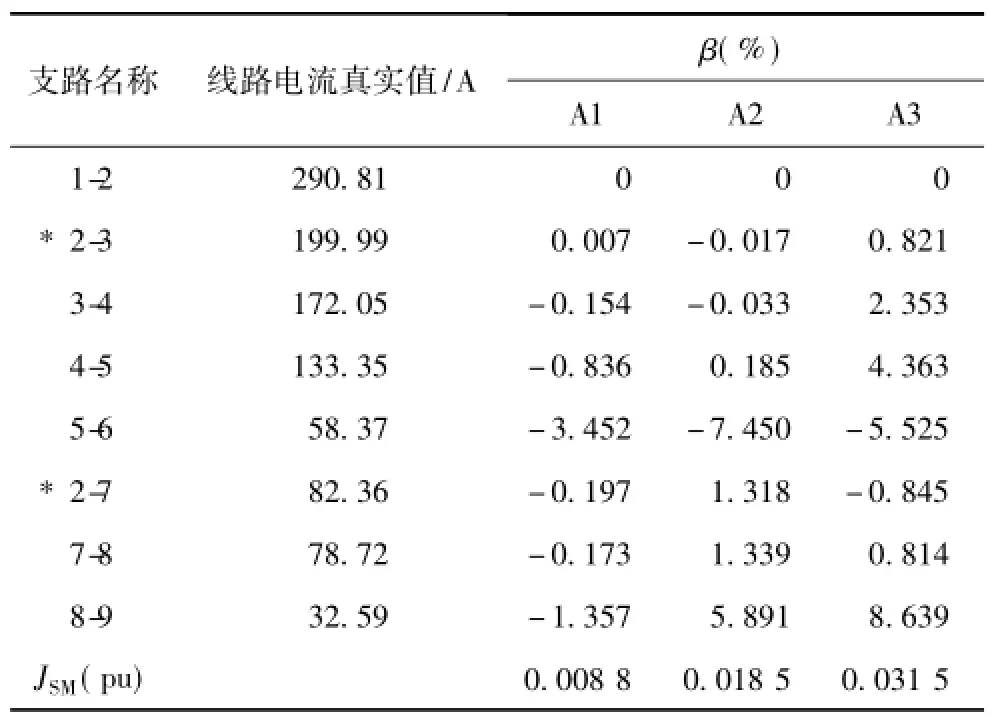
表4 可用负荷曲线近似描述情形支路电流估计结果Tab.4 Branch current estimation of load available scenarios

表5 变压器容量做上限情形电流估计结果Tab.5 Current estimation of scenarios using transformer capability as upper bound
从表4可以看出,A1、A2、A3三种情形下β都在10%范围内,对于配电线路来说是可以接受的。结合9节点线路接线图5可知,β的变化趋势是离始端节点越近其值越小,估计效果越好。这个结论具有十分重要的实践意义。
为了对配电网进行更好的管理,同时提高供电质量,网络重构和故障后快速复电等高级应用也被引入配电网中[21,22]。依据这些应用得到的配电网调整策略往往涉及到将某些地区的负荷转移到另一条配电线路上的操作。变电站内可以获得线路始端的电流,在没有安装线路电流测量装置的情况下,难以了解线路中部电流。出于成本的考虑,线路始端的线径较大,中部线路线径稍小,负荷较大时有可能出现首端线路没过载,但中部线路过载的情况。如果将负荷转移到另一条馈线后造成线路电流过大,就会引起保护装置动作,导致更大范围的停电。因此在转移负荷前需要利用状态估计得到线路当前电流的大小。本文状态估计模型对于线路中部电流的估计误差在3%以内,估计结果可以供进行转供操作的人员参考。
由表4与表5纵向对比可看出,在负荷曲线与负荷实际值相近的情形下,线路电流估计值基本满足由始端向末端变差的规律。A1中8-9线路比其上游7-8线路电流估计值偏差小一些,这是因为量测量存在一定随机性,状态估计存的结果也存在一定偏差,所以不能严格保证上游线路都比下游线路电流估计值偏差小,但总的趋势仍然是离始端越近偏差越小。
用变压器容量作上界时,始端可知情形B3的电流估计值不满足由始端向末端变差的规律。B3下离始端较近的线路3-4电流估计偏差为10.247%,线路4-5处于线路3-4的下游,是最末端的支路,偏差是7.713%,比线路3-4的偏差小很多,电流估计值的偏差没有明显的规律可循。配电网是辐射状运行,上级节点估计结果会对下级节点造成影响。电流是由负荷决定的,由于B3每个节点负荷的估计值都与实际值偏差大,偏差的累积使得电流估计值存在较大不确定性。
通过分析以上6种情形,可以总结出以下规律。
1)要想获得较好的估计结果,需要满足以下两个条件之一:①要有较多在线可用的准实时量测量。从表2和表3可看出,A1情形估计效果是最好的,随着在线可用准实时量测量的减少,A2的估计质量开始变差;②较准确的负荷上下界有利于提高状态估计的准确度。从图6、图7可看出,以负荷曲线确定不等式上下界时JSM较小,以变压器容量作为负荷不等式约束上界时,如果负荷实际值远小于变压器容量值,且这一点又没有在线可用的准实时量测值,则这一点的估计结果较差,也会影响其他没有在线可用准实时测量值节点的负荷估计值。这时因为负荷的估计值要满足潮流方程,某个节点估计的负荷变少了,另一处负荷就会估计得多,以此来实现功率平衡。分析表4和表5中的JSM也可得出以上规律,此处不再赘述。
2)支路电流估计质量由支路首端至末端逐渐变差。除了B3,其他情形下电流估计值在支路首端具有较好结果,首端到末端电流的估计结果慢慢变差。由于头节点量测量和潮流方程的引入使得估计结果偏向配电网真实状态,所以无论何种情形下,线路中部支路电流的估计值都在可接受范围内。
3)本文方法能较好地从准实时量测量中还原电压幅值真实值,无论何种情形电压幅值估计值与真实值都较接近。
A3及B3情形中都没有任何当前时刻的准实时量测,只有通过准实时量测量历史数据(典型负荷曲线)及变压器容量限制构造的不等式约束。从仿真中可看到A3及B3情形的估计结果都可以满足实践中的要求,说明本文方法可用于准实时量测在线率低的配电网。
为了进一步评价本文模型对于更大规模配电网的估计效果,利用文献[20]提供的33节点配电网算例估计每条线路的电流。该33节点算例为-12.66 kV配网系统,总负荷为3 715 kW+j2 300 kvar,有5条送电支路。仍以潮流计算的结果作为真实值,在其基础上按式(11)取σ为0.03叠加误差形成量测量。用与9节点系统相同的方法,采用负荷曲线设置33节点系统的负荷功率的上下界。与前文类似计算33节点100%可知、50%可知、始端可知3种情形下电流的估计值。电压下界取0.9,上界取1.0。50%可知选取3、5、6、9、11、12、15、17、20、21、22、23、27、29、30、31号节点没有在线可用准实时量测量。计算负荷功率、电压幅值和相角估计值与真实值的统计误差JSM,负荷功率、电压幅值估计值与测量值的统计误差JZM列于表6。计算支路电流估计偏差列于表7中。
为了与已有的配电网状态估计方法比较,采用文献[23]中的最小二乘法(WLS)做对比,仿真使用的量测量信息列在表8中。WLS的量测误差σ=0.03,统计误差结果见表6,电流估计偏差见表7。
表8中显示WLS的在线可用准实时量测是最多的。需要指出的是本文采用WLS时,在线可用的准实时数据量测冗余较高,这种情形在配电网中较少见,但为了对比仍将其考虑进来。
表6中每种情形下JSM都比JZM小,三种情形下随着量测量的减少,JSM和JZM都逐渐增大,与9节点系统结果类似。从表7中可以看出靠近线路始端的支路电流的估计结果较好。3种情形下大多数电流估计值大都在10%以内,最差的估计结果也在22%以内。100%情形下电流估计值的统计误差JSM最小,始端情形的JSM最大,50%情形的JSM处于两者之间。量测量越多估计准确度越高,仿真结果的规律与9节点系统一致。100%情形中线路31-32比上游线路30-31电流估计值稍小,但比该支路首端线路6-26的电流估计值偏差大。电流估计值偏差变化的趋势仍符合离支路首端越近,偏差越小的规律。50%和始端情形电流估计值偏差的规律与100%情形类似。通过对33节点系统的仿真,进一步验证了前文所提本文方法的特点。

表6 33节点系统负荷、电压统计误差Tab.6 Statistical error of load and voltage for 33-node network

表7 33节点系统支路电流估计结果Tab.7 Branch current estimation for 33-node network

表8 在线可用准实时量测基本信息Tab.8 Basic information about available quasi real-time measurement
从表6和表7可看到WLS的偏差最小,因为这个方法可用量测量最多,所以有比较好的估计结果。量测冗余度的高低是决定状态估计结果好坏的重要条件。在线可用准实时数据较多时,采用WLS的确可获得良好的估计结果,但在配电网中很难达到如此高的冗余度,只能作比较用。值得注意的是,表6和表7中100%情形和最小二乘法的JSM差别不大。这说明在线可用准实时数据较多时,本文方法与最小二乘法的估计结果十分接近。本文的注重点在于缺少在线可用准实时数据时的估计准确度。之前的讨论已说明,本文方法缺少在线可用准实时数据时也能获得较满意的结果。
4 收敛性分析
配电网在线状态估计方法必须有较好的收敛性,不收敛的结果没有意义。此外配电网在线状态估计计算时间应尽可能短,否则计算结果不能代表配电网实时状态。为了评价本文方法的收敛性与速度,在一台CPU为 Core i5 3.1Ghz,4G内存的台式电脑上用Matlab编写代码进行了相关测试。图10是用内点法求解33节点系统100%可知、50%可知、首端可知3种情形下状态估计的收敛曲线。内点法通常用互补间隙来判断是否收敛,当互补间隙为小于10-5时认为算法收敛[18]。同时用最大不平衡量衡量计算收敛时等式约束的满足情况。由图10可看出,随着迭代次数的增加,互补间隙减小很快,几乎每次迭代减小10倍。迭代到第9次时互补间隙已经小于10-5。

图10 33节点系统收敛曲线Fig.10 Convergence curves of 33-node network
表9是用内点法求解33节点系统100%可知、50%可知、首端可知3种情形下收敛的情况,最小二乘法的计算时间也列在内。由于WLS没有等式约束,所以没有最大不平衡量的数据。从表9中可以看出本文方法收敛后最大不平衡量十分小,即满足了潮流约束。应用内点法求解本文状态估计问题计算速度快,迭代总时间约为35 ms,1 min内可以计算上千条这样的线路,计算时间与文献[24]中结果类似。虽然本文方法较WLS计算时间多,但计算速度仍满足配电网在线状态估计的要求。

表9 33节点系统收敛情况Tab.9 Convergence condition of 33-node network
5 结论
本文利用准实时量测量和负荷曲线,构建了一种基于最优潮流的配电网状态估计程序。在不需要安装新的量测装置情况下,可使原来基本不可观的线路变为基本可观。本文模型对量测量冗余度没有要求,不仅适用于自动化程度高的配电网,也适用于处在建设初期量测装置没有完全安装到位,或者自动化程度低的配电网。通过对某市9节点配网系统和一个33节点配网系统算例进行仿真,表明本文方法在准实时量测在线率低的情况下也有理想的估计结果,估计结果可用于网络重构等高级配网应用的计算。
附录

附表1 9节点配网系统网络参数App.Tab.1 9 node distribution network system network parameters

附表2 9节点配网系统负荷参数App.Tab.2 9 node distribution network system load parameters
[1]Reddy K S,Kumar M,Mallick T K,et al.A review of integration,control,communication and metering(iccm)of renewable energy based smart grid[J].Renewable and Sustainable Energy Reviews,2014,38(5):180-192.
[2]López G,Moreno J I,Amarís H,et al.Paving the road toward smart grids through large-scale advanced meteringinfrastructures[J].ElectricPowerSystems Research,2015,120:194-205.
[3]Paul S,Rabbani M S,Kundu R K,et al.A review of smart technology(smart grid)and its features[C]// Proceedings of 2014 1st International Conference on Non-ConventionalEnergy(ICONCE),Kalyani,2014: 200-203.
[4]李兴源,魏巍,王渝红,等.坚强智能电网发展技术的研究[J].电力系统保护与控制,2009,37(17):1-7. Li Xingyuan,Wei Wei,Wang Yuhong,et al.Study on the development and technology of strong smart grid[J].Power System Protection and Control,2009,37(17):1-7.
[5]张建华,曾博,张玉莹,等.主动配电网规划关键问题与研究展望[J].电工技术学报,2014,29(2): 13-23. Zhang Jianhua,Zeng Bo,Zhang Yuying,et al.Key issues and research prospects of active distribution network planning[J].TransactionsofChinaElectrotechnical Society,2014,29(2):13-23.
[6]Baran M,Mcdermott T E.State estimation for real-time monitoring of distribution feeders[C]//2009 IEEE Power &Energy Society General Meeting,Calgary,2009:1-4.
[7]Manitsas E,Singh R,Pal B C,et al.Distribution system state estimation using an artificial neural network approach for pseudo measurement modeling[J].IEEETransactions on Power Systems,2012,27(4):1888-1896.
[8]徐玮餠,刘东,柳劲松,等.考虑质量标签的多数据源配电网状态估计算法[J].电力自动化设备,2011,31(4):78-81. Xu Weiwei,LiuDong,LiuJinsong,etal.State estimation based on quality tag for distribution network with multiple data source[J].Electric Power Automation Equipment,2011,31(4):78-81.
[9]Wu Jianzhong,He Yan,Jenkins N.A robust state estimator for medium voltage distribution networks[J]. IEEE Transactions on Power Systems,2013,28(2): 1008-1016.
[10]Haughton D A,Heydt G T.A linear state estimation formulation for smart distribution systems[J].IEEE Transactions on Power Systems,2013,28(2):1187-1195.
[11]TherrienF,KocarI,JatskevichJ.Aunified distribution system state estimator using the concept of augmented matrices[J].IEEE Transactions on Power Systems,2013,28(3):3390-3400.
[12]Pilo F,Pisano G,Soma G G.Robust distribution state estimation for active networks[C]//43rd International Universities PowerEngineeringConference,Padova,2008:1-6.
[13]Carmona-DelgadoC,Romero-RamosE,Riquelme-Santos J.Fast and reliable distribution load and state estimator[J].Electric Power Systems Research,2013,101(7):110-124.
[14]Wu Wenchuan,Ju Yuntao,Zhang Boming,et al.A distribution system state estimator accommodating large numberofamperemeasurements[J].International Journal of Electrical Power&Energy Systems,2012,43(1):839-848.
[15]Harrington P.Machine Learning in Action[M].New York:Manning Publications Company,2012.
[16]Mitchell TM.MachineLearning[M].NewYork: McGraw-Hill Inc.,1997.
[17]Ali A,Antonio G E.Power system state estimation: theory and implementation[M].New York:Basel,2004.
[18]Wei H,Sasaki H,Kubokawa J,et al.An interior point nonlinear programming for optimal power flow problemswithanoveldatastructure[J].IEEE Transactions on Power Systems,1998,13(3):870-877.
[19]程浩忠,袁青山,汪一华,等.基于等效电流量测变换的电力系统状态估计方法[J].电力系统自动化,2000,24(14):25-29. Cheng Haozhong,Yuan Qingshan,Wang Yihua,et al. A state estimation method of power systems based on equivalentcurrentmeasurementtransformation[J]. Automation of Electric Power Systems,2000,24(14): 25-29.
[20]Goswami S K,Basu S K.A new algorithm for the reconfiguration of distribution feeders for loss minimization[J].IEEE Transactions on Power Delivery,1992,7(3):1484-1491.
[21] 靳小龙,穆云飞,贾宏杰,等.面向最大供电能力提升的配电网主动重构策略[J].电工技术学报,2014,29(12):137-147. Jin Xiaolong,Mu Yunfei,Jia Hongjie,et al.An active reconfiguration strategy for distribution network basedonmaximumpowersupplycapability[J]. Transactions of China Electrotechnical Society,2014,29(12):137-147.
[22] 张浩,和敬涵,薄志谦,等.基于动态规划算法的故障恢复重构[J].电工技术学报,2011,26(12): 162-167. Zhang Hao,He Jinghan,Bo Zhiqian,et al.Service restorationbasedondynamicprogramming[J]. Transactions of China Electrotechnical Society,2011,26(12):162-167.
[23] 熊文,武鹏,余浩斌.基于负荷测录系统的配电网状态估计[J].电力系统保护与控制,2012,40(7): 84-87. Xiong Wen,Wu Peng,Yu Haobin.State estimation of distribution network by the load monitor system[J]. Power System Protection and Control,2012,40(7): 84-87.
[24] 黄伟,庞琳,曹彬,等.基于分区解耦的配电网状态估计的分布式并行计算[J].电力系统保护与控制,2014,42(15):45-51. Huang Wei,Pang Lin,Cao Bin,et al.Parallel and distributedcomputingforanarea-decoupledstate estimation method for distribution systems[J].Power System Protection and Control,2014,42(15):45-51.
A State Estimator for Smart Distribution Networks with Quasi-real Time Data
Li BinDu MengyuanZhu YunWei Hua
(Guangxi key Laboratory of Power System Optimization and Energy Technology Guangxi UniversityNanning530004China)
A novel distribution management system(DMS)architecture combined with the data mining technology and the relevant state estimation for smart distribution networks is introduced due to the fact that the measurement in the root node is highly accurate while the measurement redundancies of the rest nodes are low,some of which even have no measurements.The method proposed in this paper takes use of the quasi real-time measurements to form the objective function.The historical load curves are adopted as the inequality constraints.Unlike the traditional distribution state estimation,the proposed method is suitable for the distribution network with few on-line quasi real-time measurements.This method is a kind of state estimation whose structure is similar to the optimal power flow.So it can be solved with the interior point method.The case study is carried out with a real 9-node distribution network and the results are discussed in detail.At the same time,a widely used 33-node distribution network is also used for further validation.Simulation results show that the calculating speed and the convergence of the proposed method can realize the online state estimation in the smart distribution network.The proposed method produces satisfactory estimations in the distribution networks with a few on-line quasi real-time measurements.Especially,the current estimation meets the requirement for advanced smart distribution power applications.
State estimation,smart distribution network,data mining,interior point method
TM764
国家重点基础研究发展规划(973计划)(2013CB228205)和国家自然科学基金(51107011,51167001)资助项目。
2015-01-14改稿日期 2015-03-29
李滨女,1975年生,副教授,硕士生导师,研究方向为电力系统最优化。
E-mail:lizhen@gxu.edu.cn
杜孟远男,1988年生,硕士研究生,研究方向为状态估计。
E-mail:felix_du@188.com(通信作者)

