基于VMD和TEO的高压输电线路雷击故障测距研究

高艳丰　朱永利　闫红艳　武英杰

（1.新能源电力系统国家重点实验室（华北电力大学） 保定　071003 2.河北工程大学水电学院　邯郸　056038）

基于VMD和TEO的高压输电线路雷击故障测距研究

高艳丰1，2朱永利1闫红艳2武英杰1

（1.新能源电力系统国家重点实验室（华北电力大学） 保定071003 2.河北工程大学水电学院邯郸056038）

针对传统行波检测中小波模极大值法对于基函数和分解尺度的高要求以及希尔伯特黄变换（HHT）方法中经验模态分解（EMD）存在的模态混叠现象，提出一种基于变分模态分解和Teager能量算子相结合的高压输电线路雷击故障行波检测方法。针对行波波速及线路实际长度的不确定性给测距结果带来的影响，结合故障行波在线路中的传播途径，推导出一种新的双端行波测距算法，该算法的测距结果不受行波波速的影响。将该方法应用到雷击点和故障点定位，解决了雷击点和故障点不一致时的故障定位问题。EMTDC仿真结果验证了该方法的正确性及有效性。

行波检测变分模态分解Teager能量算子双端行波测距雷击定位

0　引言

随着社会经济的迅速发展，我国电网已迈入高电压、大容量的发展阶段。高压输电线路作为电力系统的命脉，穿越地形复杂，气候条件多变，故障事件时有发生［1-3］，雷电直接或间接作用所造成的故障约占总故障次数的40%～70%［4］。传统的人工巡线方式查找故障位置已无法满足当前电力系统发展的要求。因此，研究准确、快速的故障定位方法对电力系统的安全稳定运行具有重要意义。

近年来，国内外专家学者提出了许多输电线路的故障定位原理和算法［5-10］，有的已研制成故障定位装置并应用于现场。行波法被认为是最为准确的故障测距方法，在理论上具有较高的定位准确度，但受现场运行因素的影响，其测距准确度仍有待进一步提高。行波测距的两个关键问题即行波波头的检测和行波波速的设定。当前行波波头的检测方法主要有小波模极大值法和希尔伯特黄变换（Hilbert Huang Transform，HHT）方法。小波分析对非奇异信号的检测具有良好的效果［11-15］，但需要根据具体的问题选择合适的基函数和分解尺度，否则难以得到满意的效果。HHT方法是一种自适应的信号分解方法［5，16］，通过对信号经验模态分解（Empirical Mode Decomposition，EMD）分解得到的首个固有模态函数（IMF1），进行Hilbert变换，得到瞬时频率谱上的首个突变点即故障初始行波到达检测点的时刻。由于EMD算法本身存在模态混叠现象，当分解出的IMF不是单分量的信号时，该方法则难以准确确定行波波头的到达时刻，造成测距误差较大。文献［17，18］提出了用EEMD和ELMD方法抑制模态混叠，但并不能完全消除。

变分模态分解（Variational Mode Decomposition，VMD）是2014年最新提出的一种信号分解方法，分解模态稳定性好，能够很好地反映信号的奇异性特征，在当前输电线路故障行波特征提取的文献中尚未见到相关报道。VMD采用变分模态分解，较EMD和小波分析在很多方面都有更大的优越性。Teager能量算子（Teager Energy Operator，TEO）是一种非线性算子，能够快速准确地跟踪信号的变化，适于信号的实时检测处理。

行波波速是行波测距的另一关键问题。行波波速与输电线路参数及频率等关系密切，同一输电线在不同时刻其参数也不同，行波波速是个变化的量，在实际应用中采用光速或近似光速的值，定位误差较大，为了减少行波波速的影响，文献［19］提出了不受行波波速影响的故障定位算法，但在实际应用中，行波折射和反射现象的存在经常使行波衰减至难以检测的程度，易造成定位失败。文献［20］利用三端行波测量数据进行故障定位，前提是故障线路与相邻线路的参数（如导线型号等）必须相同，两线路的行波传播速度相同，否则定位误差较大。

本文将VMD与TEO应用到行波波头的检测，并采用新的双端行波测距算法进行故障点和雷击点定位。将所提方法与小波分析法和HHT方法进行了对比，大量EMTDC仿真验证表明，应用该检测方法能更好地检测出行波的突变，解决了雷击点和故障点不一致时的故障点定位问题，且具有较高的定位准确度。

1　基于VMD与TEO的行波检测方法

1.1VMD原理与算法［21］

1.1.1VMD原理

变分模态分解是K.Dragomiretskiy等［21］提出的一种信号处理新方法，其核心思想是变分问题。该方法在获取IMF分量时不同于EMD和LMD算法所使用的循环筛分剥离的信号处理方式，而是将信号分解过程转移到变分框架内，通过迭代搜寻变分模型最优解来确定每个分量的频率中心及带宽，从而能够自适应地实现信号的频域剖分及各分量的有效分离，突出了数据的局部特征，表现出更好的噪声鲁棒性，且具有良好的采样效应。

VMD的分解过程即变分问题的求解过程，包括变分问题的构造和求解，涉及3个重要概念:经典维纳滤波、希尔伯特变换和频率混合。

1）变分问题的构造

VMD变分问题是将分析信号f分解成K个模态函数uk（t），若每个‘模态’是具有中心频率的有限带宽，则使得每个模态的估计带宽之和最小。每个模态的带宽，按以下步骤估算:

（1）通过Hilbert变换，计算每个模态函数uk（t）的解析信号，得到其单边频谱。

（2）将每个模态的频谱调制到相应的基频带，通过混合预估中心频率e-jωkt。

（3）计算上述解调信号梯度的平方L2范数，估计各模态信号带宽。

假定将原始信号f分解为K个IMF分量，则对应的约束变分模型表达式为

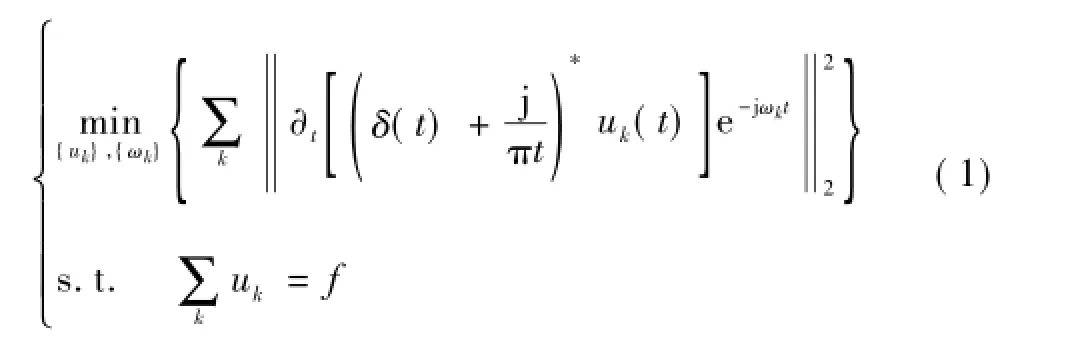
式中，｛uk｝为分解得到的K个IMF分量，｛uk｝=｛u1，…，uK｝；｛ωk｝为各分量的频率中心，｛ωk｝=｛ω1，…，ωK｝。

2）变分问题的求解

（1）引入二次惩罚因子α和Lagrange乘法算子λ（t），将约束性变分问题变换为非约束性变分问题，得到的增广Lagrange表达式为

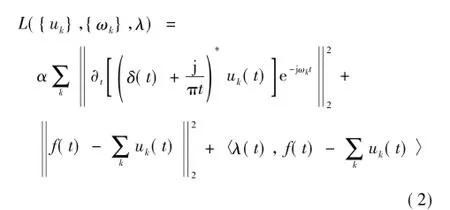
（2）利用交替方向乘子算法求取上述增广Lagrange函数的鞍点，即为式（2）的最优解，从而将原始信号f分解为K个窄带IMF分量。

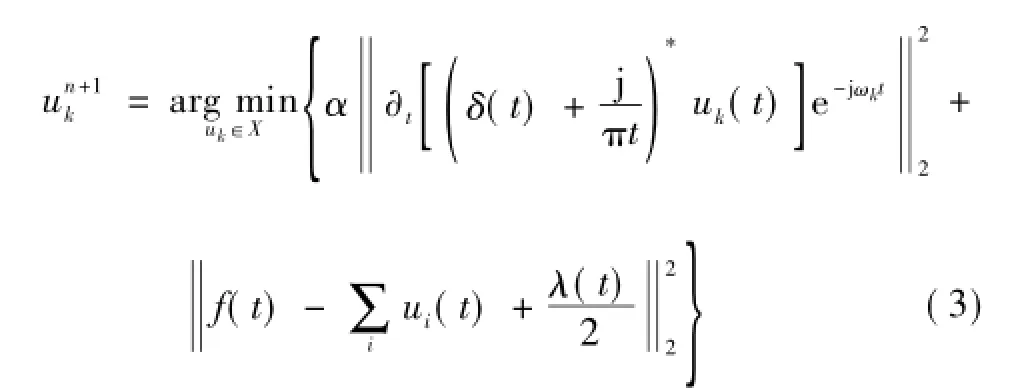
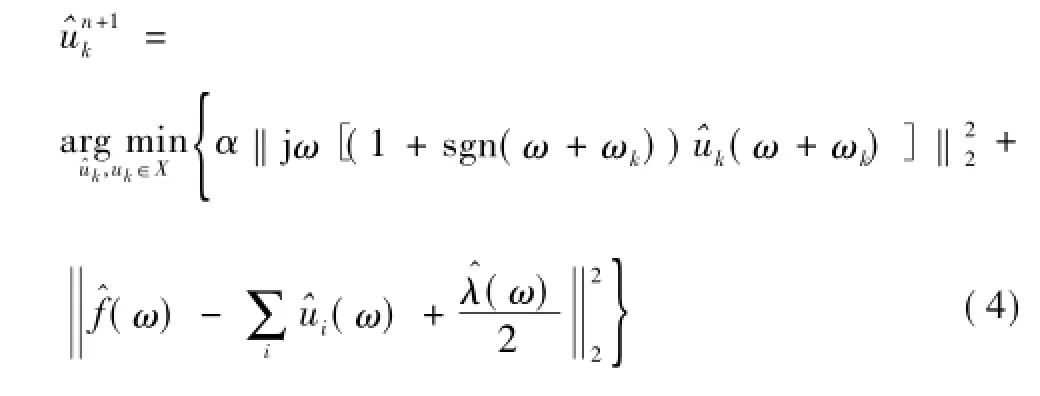
用ω-ωk代替式（4）第一项的ω，有

将式（5）写成非负频率区间积分的形式

通过二次优化很容易得到频率的解

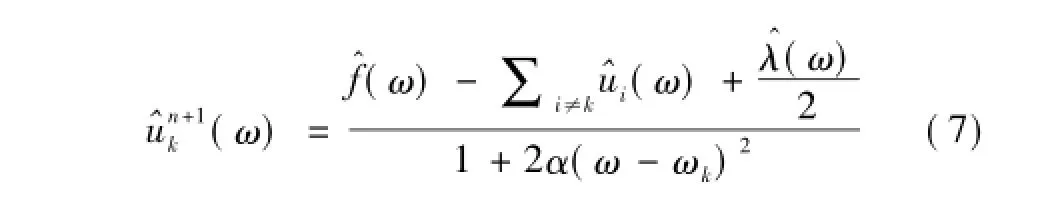
同理，用中心频率表达时，当中心频率ωk仅出现在重构信号的带宽表达项时，相关问题可描述为

求解得

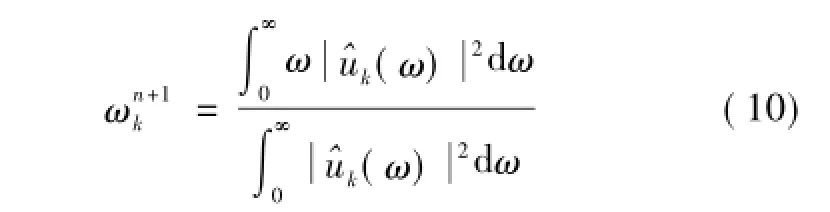
1.1.2VMD算法流程

2）n=n+1，执行循环。

3）根据式（7）或式（10）更新uk和ωk。

4）k=k+1，重复步骤3），直至k=K结束。

5）根据式（11）更新λ。

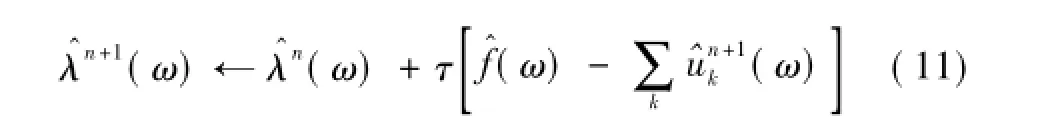
VMD算法简单，各模态在频域不断得到更新，最后通过傅里叶逆变换到时域。作为各模态的功率谱重心，中心频率被重新预估，并以此循环更新，当分解结果对保真度要求较低时，可将τ置为零。

1.2Teager能量算子［22，23］

Teager能量算子是一种非线性算子，计算量小，能快速准确地跟踪信号的变化，适于信号的实时检测处理。根据这一特点，利用TEO获取信号能量的瞬时变化，瞬时频率谱上的首个突变点对应时刻即故障初始行波到达检测点的时刻。若信号为s（t），TEO可定义为

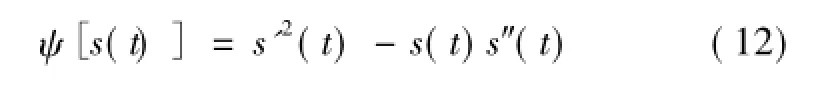
式中，s'（t）为s（t）的导数；ψ为能量算子。

对于离散信号，式（12）可近似表示为式（13）所示的形式。

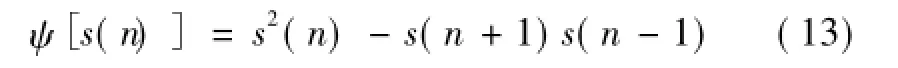
1.3基于VMD与TEO的行波检测实例

输电线路发生雷击或故障时，产生的暂态行波信号是具有突变性的非平稳信号，故障行波检测即提取故障初始行波到达检测点的特征。本文将VMD与TEO应用于行波故障测距中的初始行波波头检测，为故障测距提供可靠数据。

例如某220 kV的输电系统，假设线路上距离检测点40 km处发生A相短路故障，取故障后2 ms的电流行波信号进行分析，采样频率为1 MHz。考虑到线路三相之间的耦合作用，首先利用Clarke变换进行解耦，然后对解耦后的电流线模分量进行VMD分解，变分模态分解参数设置:K=3，α=2 000，τ=0。分析信号及其VMD分解结果如图1所示。

图1　分析信号及其VMD分解结果Fig.1　Analytical signal and itsVMD decomposition results

由图1可知，模态1反映了信号的变化趋势，仿真表明，模态1基本保持不变，不随模态数量K的增加而变化，因此计算模态1的瞬时Teager能量算子值。模态1的瞬时能量谱如图2所示。

图2　模态1的瞬时能量谱Fig.2　Instantaneous energy spectrum of modal 1

由图2可知，故障初始行波在t=135 μs时到达检测点，从而达到检测故障行波初始波头的目的。同理，上述分析信号的小波分析方法和HHT方法检测结果如图3、图4所示。

图3　小波模极大值检测结果Fig.3　The test results of Wavelet modulus maxima

图4　HHT方法检测结果Fig.4　The test results of HHT method

由图3可知，小波模极大值分析时，随着选择的基函数和分解尺度不同，检测的结果也不同，不同层的小波系数的模极大值点存在差异，选择哪一层作为检测结果需要做出合理的判断。如图4所示，HHT方法检测行波波头时，由于EMD分解存在模态混叠现象，当采样电流行波的极值点少于3个时，IMF1即信号本身，其Hilbert变换得到的瞬时频率谱无法检测到故障行波到达检测点的时刻，从而造成故障测距失败或误差较大。通过上述图形比较，采用VMD与TEO相结合的方法时，检测结果相比小波模极大值法和HHT方法效果好。

2　双端行波测距新算法

双端行波测距算法利用故障点产生的行波到达两端的时间差和波速来确定故障位置，其原理如图5所示。

图5　双端行波定位原理图Fig.5　Double-terminal traveling wave location schematics

测距公式为

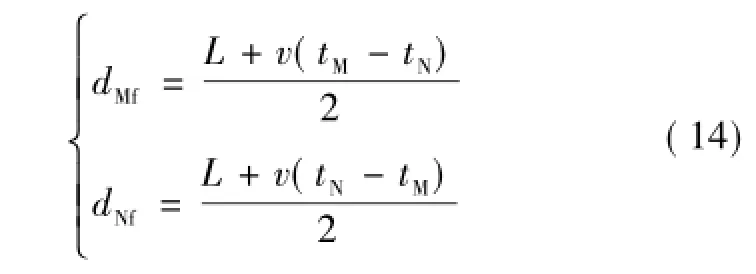
式中，L为线路的长度；tM、tN分别为故障初始行波到达M、N两端检测点的时刻；v是行波波速。

由式（14）可知，行波故障定位的准确度与线路的实际长度、行波波速及行波波头的到达时刻密切相关。输电线路架设过程中，电力线每档的实际长度一般大于杆塔水平距离的5%以上［19］，线路实际长度随温度和气候环境变化，难以确定。工程中实际给出的线路长度为每档线路水平距离之和，直接应用此长度进行定位，必然给定位结果带来较大误差。另外，行波波速是一个不确定的量，在以往的计算中，波速取某一接近光速的值，难免会给定位结果带来较大误差。为此，需要从行波的实际传播途径出发，把实际故障距离长度转换到故障在线路水平距离的位置。

若同一条线路的导线型号相同，则杆塔之间的导线在相同季节的伸缩是均匀的，所以故障点到导线一端的水平距离同杆塔档距长度的比例近似等于故障点到该端实际导线长度与导线实际全长的比值。假设输电线路水平距离为L，故障发生时刻为t0，故障初始行波到达M、N两端检测点的时刻分别为tM、tN，行波在线路中传播的速度为v，则行波传播的实际距离即为输电线路的实际长度L'为

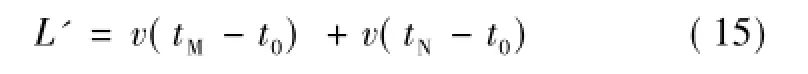
故障点距离M点的实际长度为

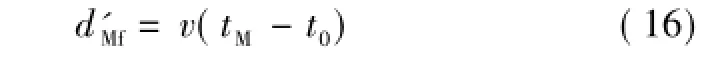
故障在线路水平距离上位置为dMf，则有

则故障位置显示为

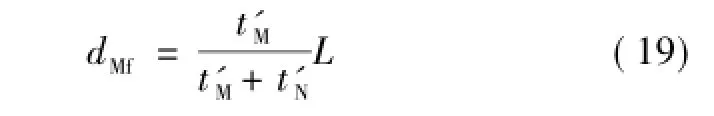
由式（19）可知，测距结果仅与故障初始行波到达两端检测点的时刻和给定线路长度有关，不受行波速度和输电线路实际长度变化的影响。与当前不受行波波速影响的定位方法相比，该算法避免了故障反射波的测量，故障定位更可靠。

3　雷击故障测距分析

输电线路故障测距包括故障类型的识别以及雷击点和故障点的定位。关于故障类型的识别，文献［24-30］中已有详细说明，本文不再赘述。若为雷击类型，在雷击识别的基础上可进行雷击点和故障点定位。输电线路发生雷击后大致分两种情况分析:①当雷电流幅值较小时，雷击导线并未造成线路故障，称为雷击干扰，为加强防雷保护，可应用上述方法直接定位雷击点；②雷击输电线路造成故障，对雷击故障又可分两种情况讨论。雷电流较大时，导致雷击点与故障点相同，对雷击点和故障点的定位同上；雷电流较小时，雷击线路后并未马上发生闪络，雷电波向线路两侧传播，在绝缘薄弱处发生故障，如图6所示。

图6　雷击点与故障点不同时的情况Fig.6　Case of lightning strike point and the point of failure is inconsistent

根据文献［31］所述，利用线路两侧采样的电流波形的相关系数，可判断雷击点和短路点位置是否相同。当雷击点与故障点不同时，判断出雷击侧，在雷击点定位的基础上确定短路点位置。利用雷击侧检测到的两个行波到达时间差计算短路点到雷击点的距离。

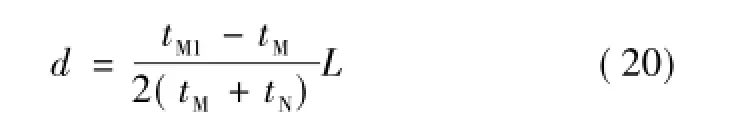
4　仿真验证

图7是在PSCAD/EMTDC环境下建立的某电网220 kV输电系统仿真模型。

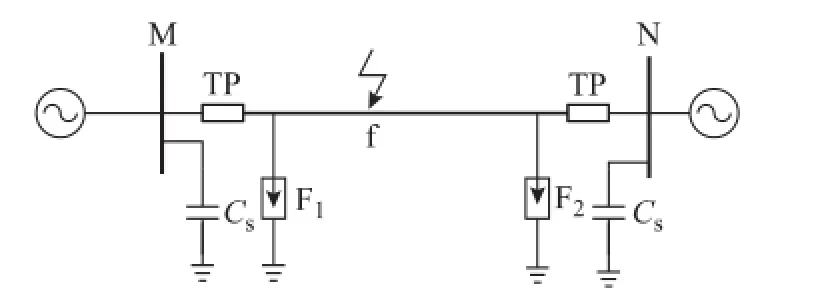
图7　220 kV输电系统仿真模型Fig.7　Simulation model of 220 kV transmission systems

输电线路为频率相关模型，杆塔间的水平距离为105 km，三相导线均匀换位，且全线架设双避雷线。杆塔档距假设为3.5 km，考虑线路避雷器对行波的影响，在线路两端装有避雷器F1、F2，避雷器采用IEEE推荐的非线性模型；TP为暂态保护；Cs为母线对地杂散电容，取值0.01 μF［24］；绝缘子的闪络电压为1 200 kV。电流互感器对高频信号的传变特性比电压互感器好，采样时取电流信号，采用Clarke变换取模信号进行分析。采样频率为1 MHz，取故障后2 ms的数据。下面就两种雷击故障情况进行分析。

1）当高压输电线发生雷击干扰、雷击故障和短路时，雷击点与故障点位置相一致。

假设在距离M端35 km处f点发生短路及雷击，雷电流采用国际电工委员会（IEC）规定的2.5/50 μs标准波形。线路M、N两端测得的3种状态下的α模（线模）电流波形以及VMD分解得到的模态1和TEO瞬时能量谱，如图8～图13所示。

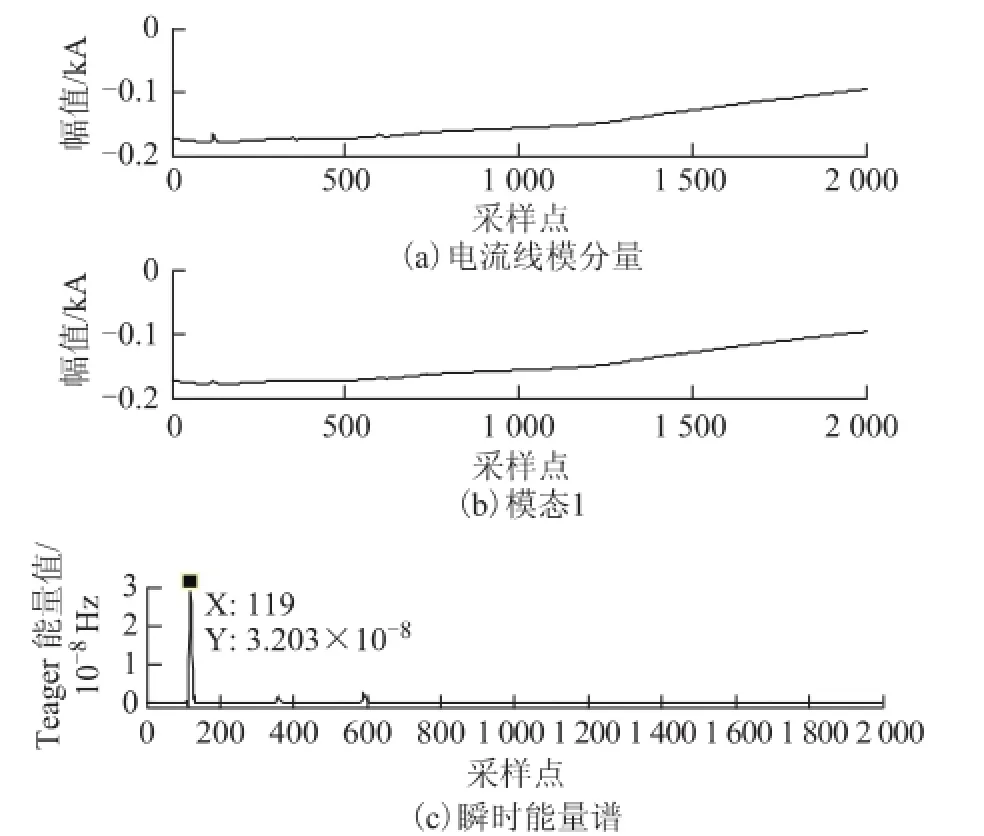
图8　短路时M端检测结果Fig.8　M-side test results when short circuit

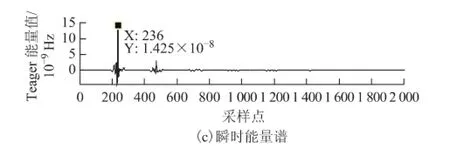
图9　短路时N端检测结果Fig.9　N-side test results when short circuit

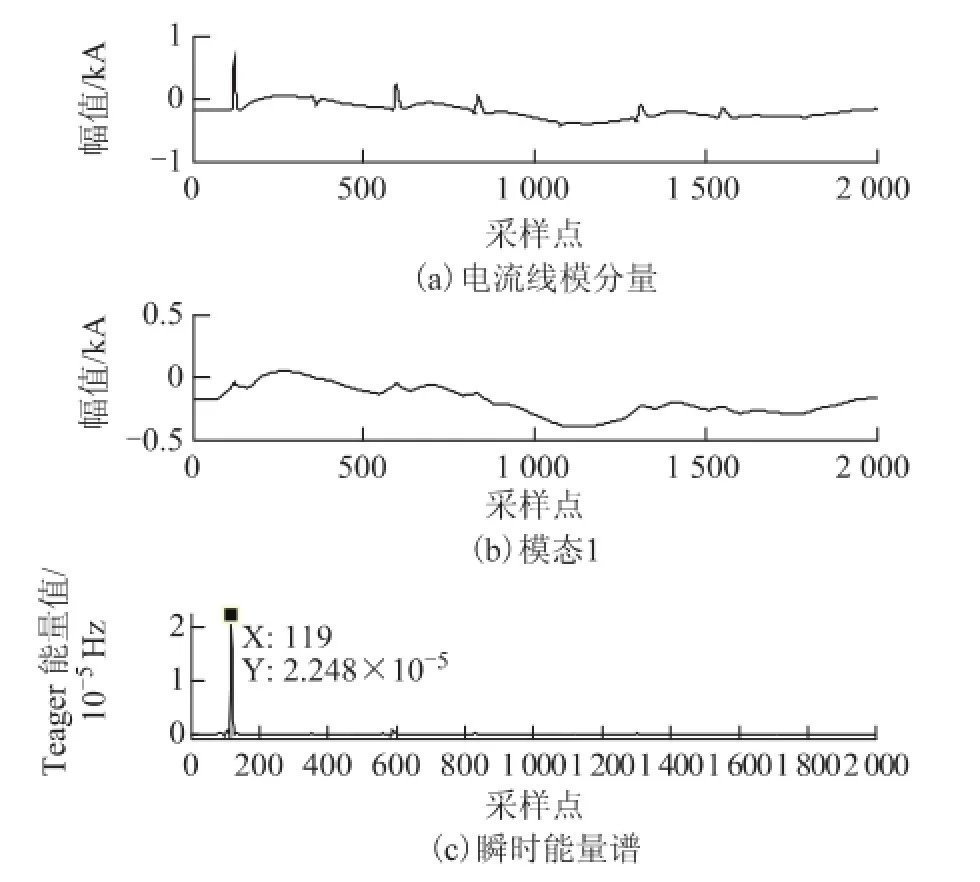
图10　雷击干扰时M端检测结果Fig.10　M-side test results when lightning interference

图11　雷击干扰时N端检测结果Fig.11　N-side test results when lightning interference

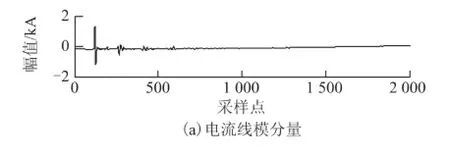
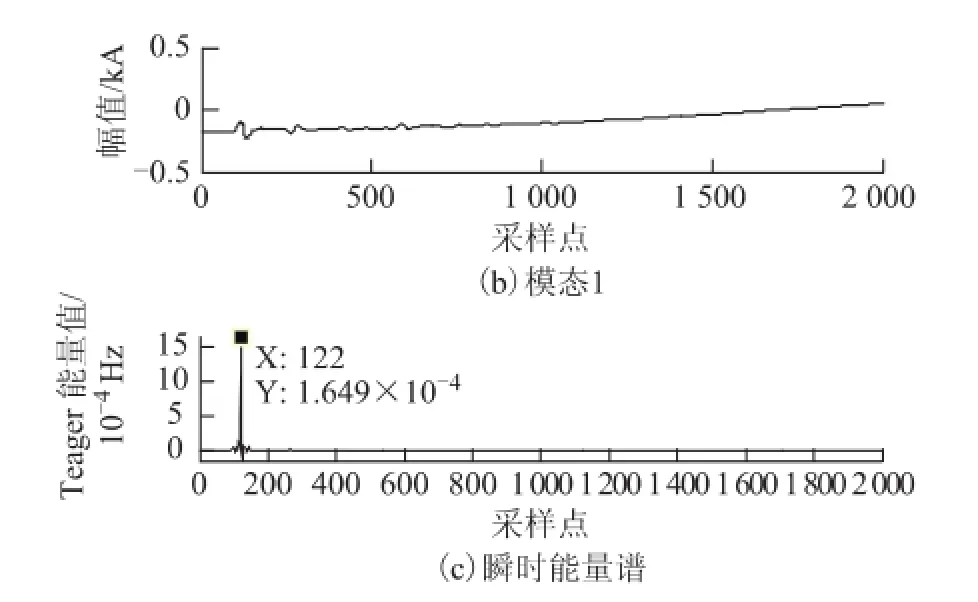
图12　雷击故障时M端检测结果Fig.12　M-side test results when lightning fault

图13　雷击故障时N端检测结果Fig.13　N-side test results when lightning fault

从图8～图13中可清晰地检测到故障行波到达检测点的时刻。将数据代入行波测距公式有:

（1）线路发生A相短路时，测距结果为

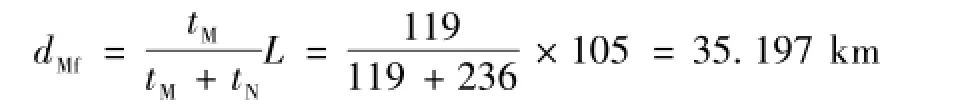
（2）线路发生雷击干扰时，雷击点的测距结果为

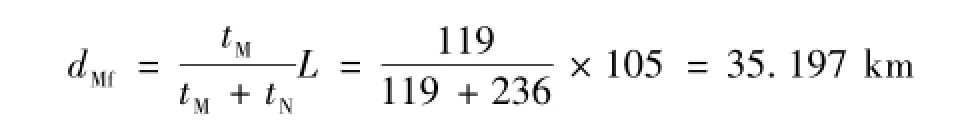
（3）线路发生雷击故障时，故障点的测距结果为

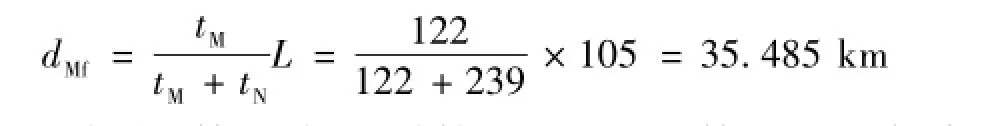
从测距结果看，3种情况下的测距结果误差分别为+0.197 km、+0.197 km和+0.485 km。测距结果比较理想，能够满足实际工作需要。

为了验证该方法的正确性和具有高的测距准确度，假设距离M端测点不同位置发生不同类型的短路故障，在短路条件和雷电流等条件不同时进行了大量仿真，限于篇幅，本文只列出短路过渡电阻为100 Ω、雷电流为2.6/50 μs的标准波形时仿真结果如表1所示。

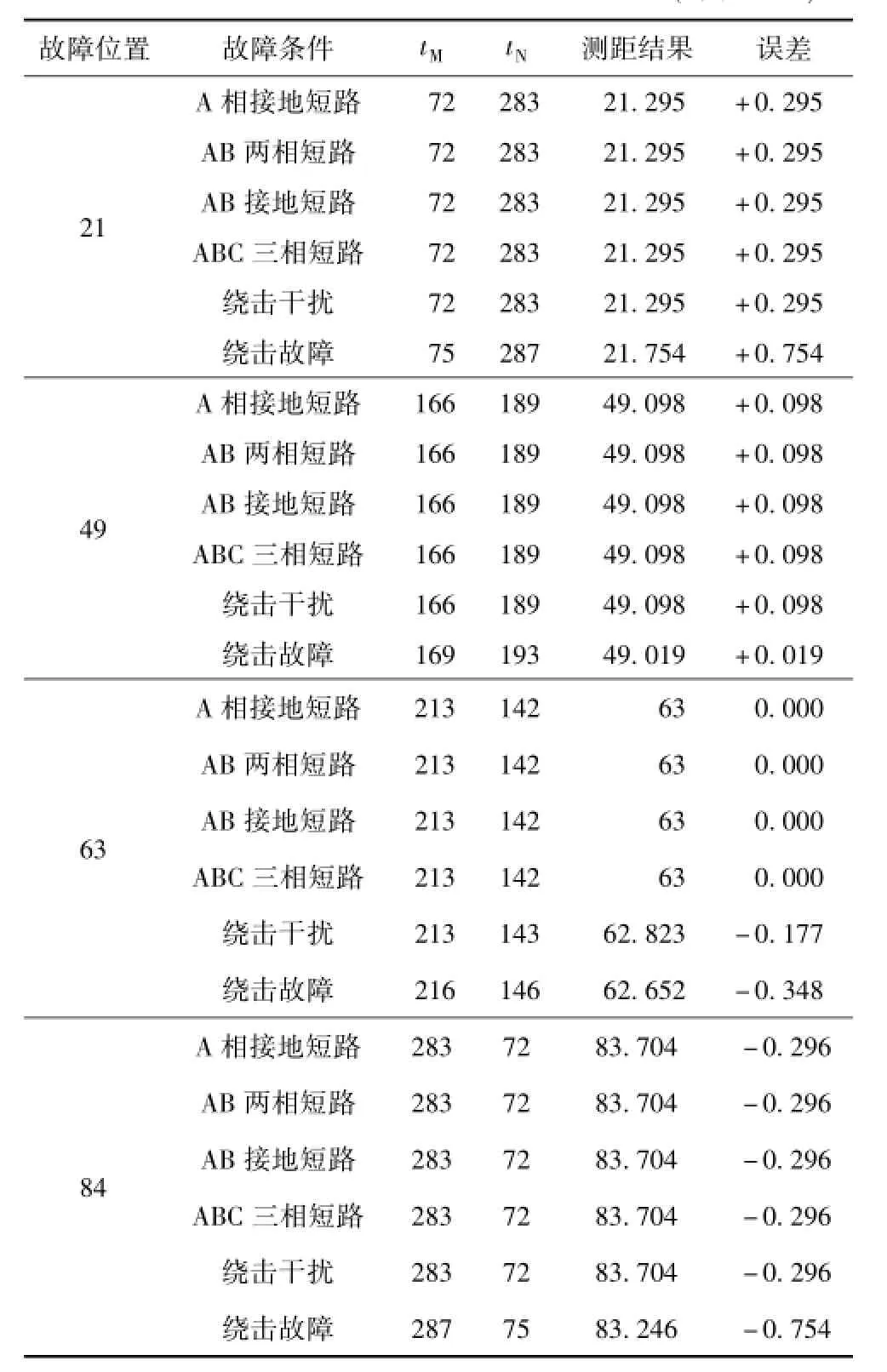
表1　不同条件下的故障测距结果Tab.1　Fault location results under different conditions（单位:km）

仿真结果表明，该方法不受短路类型和过渡电阻大小的影响，发生短路和雷击干扰时，定位准确，发生雷击故障时，受两端母线分布电容、绝缘击穿和建立电弧时间的影响，从而导致行波到达两端测点的时间略有增加，一般为3～4 μs，所以雷击定位误差较大。故障点和雷击点越靠近线路中间位置，定位准确度越高，最小误差为零；当故障点靠近两端测点时，误差相应增大。

2）当输电线路发生故障性雷击，雷击点与故障点不一致时，讨论故障点的定位问题。

假设在距离M端35 km发生雷击，当雷电波向N端传播3.5 km发生闪络，雷击侧和故障侧的信号检测结果如图14、图15所示。

雷击点的位置为

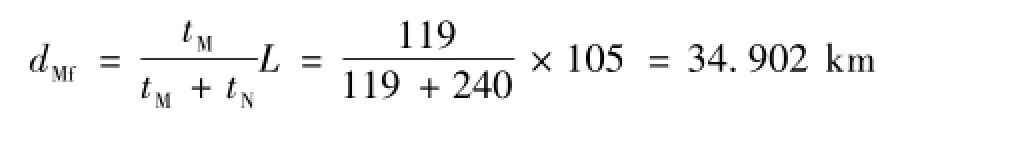
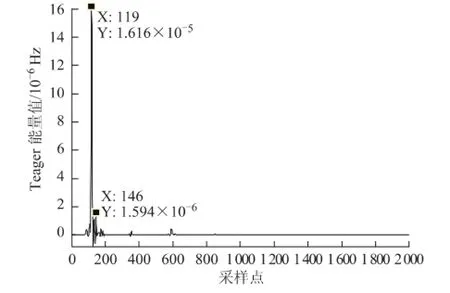
图14　雷击侧的检测结果Fig.14　The test results of lightning side

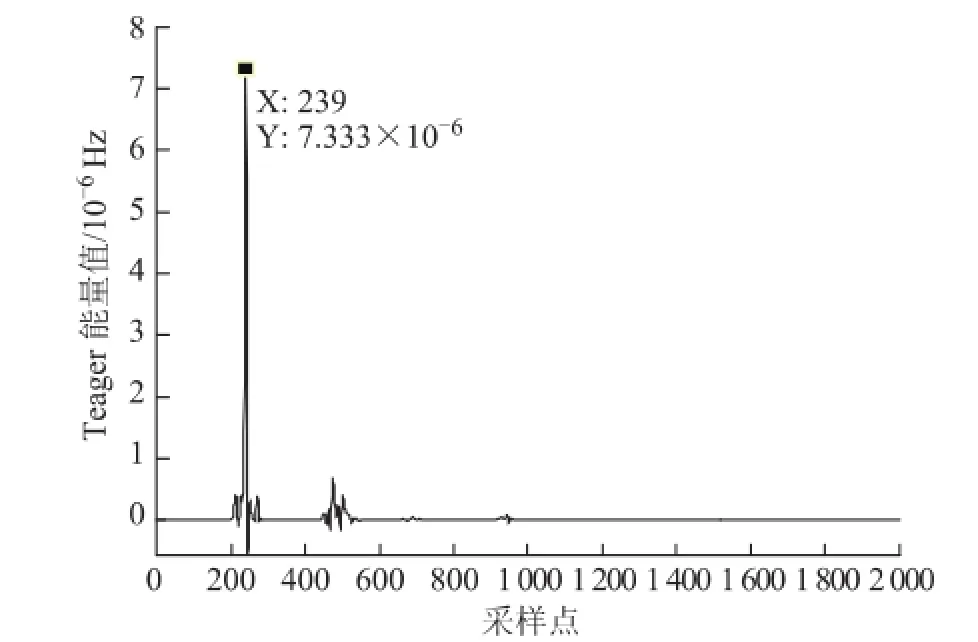
图15　雷击故障侧的检测结果Fig.15　The test results of fault side when lightning

误差约-0.195 km，故障点到雷击点的距离为

因此，故障点到M端测点的距离为38.861 km，定位误差为-0.100 km。针对第二种情况，设在距离M端21 km、49 km、63 km和84 km 4个位置发生雷击时的测距结果如表2所示。

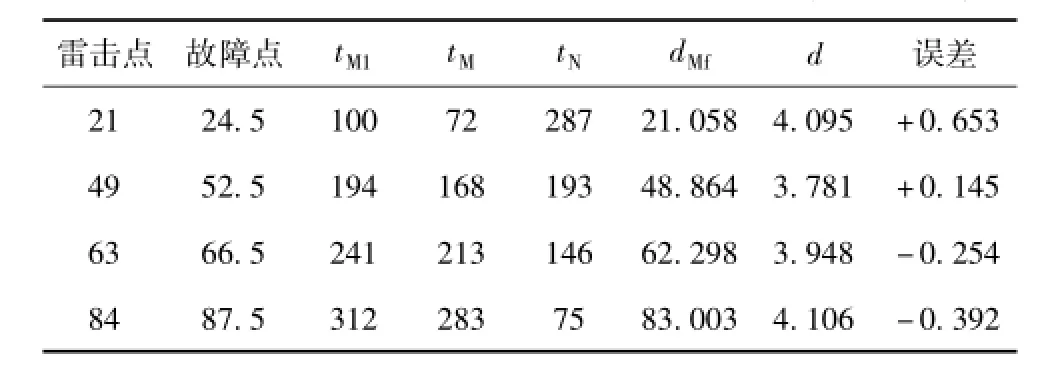
表2　雷击点与故障点位置不一致时的测距结果Tab.2　The location results of lightning strike point and fault point is inconsistency（单位:km）

由图14、图15可知，雷击侧检测到的时间与发生雷击干扰时相同，故障侧由于绝缘击穿和建立电弧，检测到的时间比雷击干扰时长。故障点位置靠近线路中间时，测距误差较小。随着故障点向线路两端靠近，测距误差增大，但整体误差在工程允许范围内。

5　结论

1）针对小波分析对于基函数和分解尺度的高要求以及HHT方法中EMD分解存在的模态混叠现象，提出一种基于VMD与TEO的行波波头检测方法。仿真比较表明，本文所提检测方法对行波突变点的检测效果更好。

2）综合考虑了故障行波在线路中传播的实际情况，推导出一种新的双端行波故障测距算法，测距结果不受行波波速和线路实际长度变化的影响。与当前不受行波波速影响的输电线路故障定位算法相比，不用考虑行波反射波的影响，定位更可靠。

3）在故障类型识别的基础上，将基于VMD和TEO的高压输电线路雷击故障测距方法应用于雷击点和故障点定位，针对性地解决了雷击故障定位中的雷击点与故障点位置不一致的故障点定位。仿真结果表明，该方法在短路故障测距及雷击干扰时的雷击点的定位具有较高的定位准确度，定位误差在工程允许范围内。

［1］易辉，崔江流.我国输电线路运行现状及防雷保护［J］.高电压技术，2001，27（6）:44-50. Yi Hui，Cui Jiangliu.The present state and lighting protectionoftransmissionlineinChina［J］.High Voltage Engineering，2001，27（6）:44-50.

［2］陈家宏，张勤，冯万兴，等.中国电网雷电定位系统与雷电监测网［J］.高电压技术，2008，34（3）: 425-431. Chen Jiahong，ZhangQin，FengWanxing，etal. Lightning location system and lightning detection network of China power grid［J］.High Voltage Engineering，2008，34（3）:425-431.

［3］董杏丽，葛耀中，董新洲.行波保护中雷电干扰问题的对策［J］.中国电机工程学报，2002，22（9）:74-78. Dong Xingli，Ge Yaozhong，Dong Xinzhou.Effect of lighting on protection based on traveling waves［J］. Proceedings of the CSEE，2002，22（9）:74-78.

［4］梅贞，陈水明，顾勤炜，等.1998～2004年全国雷电灾害事故统计［J］.高电压技术，2007，33（12）: 173-176. Mei Zhen，Chen Shuiming，Gu Qinwei，et al.Statistic of lightning accidents during 1998～2004 in China［J］. High Voltage Engineering，2007，33（12）:173-176.

［5］徐俊明，汪芳宗，尹星，等.基于Hilbert-Huang变换的行波法高压输电线路故障定位［J］.电力系统保护与控制，2012，40（2）:88-93. Xu Junming，Wang Fangzong，Yin Xing，et al.A traveling wave fault location method for high voltage power transmission lines based on Hilbert-Huang transform［J］.Power System Protection and Control，2012，40（2）:88-93.

［6］束洪春，高峰，李卫东.利用单端工频量的高压输电线路故障测距实用方法研究［J］.电工技术学报，1998，13（5）:9-15. Shu Hongchun，Gao Feng，Li Weidong.A practical fault location algorithm for HV transmission Line using one end data［J］.Transactions of China Electrotechnical Society，1998，13（5）:9-15.

［7］李泽文，曾祥君，徐晓菁，等.输电线路双端行波故障定位新算法［J］.电力系统自动化，2006，30（15）:40-43. Li Zewen，Zeng Xiangjun，Xu Xiaojing，et al.New fault location algorithm based on double terminal traveling waves for transmission lines［J］.Automation of Electric Power System，2006，30（15）:40-43.

［8］朱永利，范新桥，尹金良.基于三点电流测量的输电线路行波故障定位新方法［J］.电工技术学报，2012，27（3）:260-268. Zhu Yongli，Fan Xinqiao，Yin Jinliang.A new fault location scheme for transmission lines based on traveling waves of three measurements［J］.Transactions of China Electrotechnical Society，2012，27（3）:260-268.

［9］覃剑.输电线路单端行波故障测距的研究［J］.电网技术，2005，29（15）:65-70. Qin Jian.Study on single terminal traveling wave fault location of transmission line［J］.Power System Technology，2005，29（15）:65-70.

［10］董新洲，刘建政，余学文.输电线路暂态电压行波的故障特征及其小波分析［J］.电工技术学报，2001，16（3）:57-61. DongXinzhou，LiuJianzheng，YuXuewen.Fault characteristics and wavelets analysis of the transient voltagetravellingwaves［J］.TransactionsofChina Electrotechnical Society，2001，16（3）:57-61.

［11］马丹丹，王晓茹.基于小波模极大值的单端行波故障测距［J］.电力系统保护与控制，2009，37（3）: 55-59. Ma Dandan，Wang Xiaoru.Single terminal methods of traveling wave fault location based on wavelet modulus maxima［J］.PowerSystemProtectionandControl，2009，37（3）:55-59.

［12］ 郑州，吕艳萍，王杰，等.基于小波变换的双端行波测距新方法［J］.电网技术，2010，34（1）:203-207. Zheng Zhou，Lü Yanping，Wang Jie，et al.A new two terminal traveling wave fault location method based on wavelet transform［J］.Power System Technology，2010，34（1）:203-207.

［13］ 覃剑，陈祥训，郑健超，等.利用小波变换的双端行波测距新方法［J］.中国电机工程学报，2000，20（8）:7-11. Qin Jian，Chen Xiangxun，Zheng Jianchao，et al.A new double terminal method of traveling wave fault location using wavelet transform［J］.Proceedings of the CSEE，2000，20（8）:7-11.

［14］ 董新洲，葛耀中，徐丙垠.输电线路暂态电流行波的故障特征及其小波分析［J］.电工技术学报，1999，14（1）:59-62. DongXinzhou，GeYaozhong，XuBingyin.Fault characteristics of transient current travelling waves and its analysis with wavelets transform［J］.Transactions of China Electrotechnical Society，1999，14（1）:59-62.

［15］ 黄子俊，陈允平.基于小波变换模极大值的输电线路单端故障定位［J］.电力自动化设备，2005，25（2）:10-13. Huang Zijun，Chen Yunping.Non-communication fault locating of transmission line based on wavelet modulus maxima［J］.ElectricPowerAutomationEquipment，2005，25（2）:10-13.

［16］ 范新桥，朱永利，卢伟甫.基于EMD-TEO的输电线路行波故障定位［J］.电力系统保护与控制，2012，40（9）:8-13. Fan Xinqiao，Zhu Yongli，Lu Weifu.Traveling wave based fault location for transmission lines based on EMDTEO［J］.Power System Protection and Control，2012，40（9）:8-13.

［17］ 张玲玲，廖红云，曹亚娟，等.基于EEMD和模糊C均值聚类算法诊断发动机曲轴轴承故障［J］.内燃机学报，2011，29（4）:332-336. Zhang Lingling，Liao Hongyun，Cao Yajuan，et al. Diagnosis on crankshaft bearing fault based on EEMD and fuzzy C mean clustering arithmetic［J］.Transaction on Csice，2011，29（4）:332-336.

［18］ 康守强，王玉静，杨广学，等.基于经验模态分解和超球多类支持向量机的滚动轴承故障诊断方法［J］.中国电机工程学报，2011，31（14）:96-102. Kang Shouqiang，Wang Yujing，Yang Guangxue，et al. Rolling bearing fault diagnosis method using empirical mode decomposition and hypersphere multiclass supportvector machine［J］.Proceedings of the CSEE，2011，31（14）:96-102.

［19］蒋涛，陆于平.不受波速影响的输电线路单端行波故障测距研究［J］.电力自动化设备，2004，24（12）: 29-32. Jiang Tao，Lu Yuping.Study of fault location based on single terminal traveling waves avoiding wave speed influence［J］.Electric Power Automation Equipment，2004，24（12）:29-32.

［20］张峰，梁军，张利，等.基于三端行波测量数据的输电线路故障测距新方法［J］.电力系统自动化，2008，32（8）:69-72. Zhang Feng，LiangJun，ZhangLi，etal.Novel method about traveling wave fault location based on treble terminal measurement data for transmission lines［J］. Automation of Electric Power System，2008，32（8）: 69-72.

［21］Dragomiretskiy K，Zosso D.Variational mode decomposition［J］.IEEE Transactions on Signal Processing，2014，62（3）:531-544.

［22］Teager H M.Some observations on oral air flow during phonation［J］.IEEE Transactions on Acoustics，Speech and Signal Processing，1980，28（5）:599-601.

［23］Maragos P，Kaiser J F，Quatieri T F.Energy separation in signal modulations with applications to speech analysis［J］.IEEE Transactions on Signal Processing，1993，41（10）:3024-3051.

［24］朱永利，梁泽慧，杨慧凌，等.输电线路行波故障定位中雷击干扰与故障的识别［J］.华北电力大学学报，2013，40（3）:1-6. ZhuYongli，LiangZehui，YangHuiling，etal. Identification between fault and non-fault lightning strikes for fault location of a transmission line by traveling waves［J］.Journal of North China Electric Power University，2013，40（3）:1-6.

［25］邹贵彬，高厚磊，朱峰，等.输电线路雷击与故障的积分识别方法［J］.电力系统保护与控制，2012，40（9）:43-48. Zou Guibin，Gao Houlei，Zhu Feng，et al.Integral identification method of lighting stroke and fault for transmissionline［J］.PowerSystemProtectionand Control，2012，40（9）:43-48.

［26］司大军，束洪春，陈学允，等.输电线路雷击的电磁暂态特征分析及其识别方法研究［J］.中国电机工程学报，2005，25（7）:64-69. Si Dajun，Shu Hongchun，Chen Xueyun，et al.Study on characteristics and identification of transients on transmissionlinescausedbylightningstroke［J］. Proceedings of the CSEE，2005，25（7）:64-69.

［27］ 吴昊，肖先勇，邓武军.输电线路行波测距中雷击与短路故障的识别［J］.高电压技术，2007，33（6）: 63-67. Wu Hao，Xiao Xianyong，Deng Wujun.Identification of lighting strike and fault in the traveling wave location of transmission line［J］.High Voltage Engineering，2007，33（6）:63-67.

［28］ 吴昊，肖先勇，沈睿佼.小波能量谱和神经网络法识别雷击与短路故障［J］.高电压技术，2007，33（10）:64-68. Wu Hao，XiaoXianyong，ShenRuijiao.Lightning strike and fault identification by the wavelet energy spectrum and neural network method［J］.High Voltage Engineering，2007，33（10）:64-68.

［29］ 吕艳萍，刘亚东.应用数学形态学方法分析识别特高压线路雷击干扰［J］.高电压技术，2010，36（12）:2948-2953. Lü Yanping，Liu Yadong.New scheme to identify lightning interference for UHV transmission lines using mathematical morphology［J］.High Voltage Engineering，2010，36（12）:2948-2953.

［30］ 郭宁明，覃剑，陈祥训.雷击对行波故障测距的影响及识别［J］.电力系统自动化，2008，32（5）: 76-79. Guo Ningming，Qin Jian，Chen Xiangxun.Lighting strike identification and its effects on the traveling wave fault location［J］.Automation of Electric Power Systems，2008，32（5）:76-79.

［31］ 郭宁明，覃剑.输电线路雷击故障情况下的短路点定位方法［J］.电力系统自动化，2009，33（10）: 74-78. Guo Ningming，Qin Jian.Locating method of short circuit point for transmission lines under lightning stroke fault［J］.Automation of Electric Power Systems，2009，33（10）:74-78.

Study on Lighting Fault Locating of High-voltage Transmission Lines Based on VMD and TEO

Gao Yanfeng1，2Zhu Yongli1Yan Hongyan2Wu Yingjie1
（1.State Key Laboratory of Alternate Electrical Power System With Renewable Energy Sources（North China Electric Power University） Baoding071003China 2.School of Water Resources and HydropwerHebei University of EngineeringHandan056038China）

In view of high requirements for the basis function and the decomposition scale of the wavelet modulus maxima method and the modal aliasing phenomenon existed in empirical mode decomposition of Hilbert Huang transform method in traditional traveling-wave detection approaches，a new detection method based on the variational mode decomposition（VMD）and the Teager energy operator（TEO）for high voltage transmission line lightning fault locating is proposed.To eliminate the impact of the uncertainty of the wave velocity and the actual line length on distance measurement，a novel double-terminal traveling wave distance measuring algorithm combined with the propagation route of the fault traveling wave in the transmission line is deduced，which will not be affected by the wave velocity.This method can solve the fault locating problem successfully when the lightning strike point and the fault point are inconsistent.Abundant EMTDC simulation results verify the correctness and the effectiveness of the proposed method.

Traveling-wave detection，variational mode decomposition，Teager energy operator，doubleterminal traveling wave distance measurement，lighting fault locating

TM726

中央高校基本科研业务费专项资金资助项目（2014xs74）。2015-03-17改稿日期 2015-05-07

高艳丰男，1979年生，博士研究生，讲师，研究方向为输电线路故障定位及电力系统运行、分析和控制。

E-mail:gaoyanfeng01@126.com（通信作者）

朱永利男，1963年生，教授，博士生导师，研究方向为输变电设备状态在线监测、智能分析和智能电网。

E-mail:yonglipw@163.com