含双馈风电机组的电力系统故障计算方法研究

肖　繁　张　哲　尹项根　杨　航　杨增力

（1.强电磁与新技术国家重点实验室（华中科技大学） 武汉　430074 2.国网湖北省电力公司　武汉　430077）

含双馈风电机组的电力系统故障计算方法研究

肖繁1张哲1尹项根1杨航1杨增力2

（1.强电磁与新技术国家重点实验室（华中科技大学） 武汉430074 2.国网湖北省电力公司武汉430077）

双馈风电机组馈出的短路电流特性极其复杂，传统以交流同步电机供电电源为基础的电网故障分析方法不能适用于含双馈电源的电网短路计算。根据双馈风电机组低压穿越运行的技术要求，在电网对称故障和不对称故障条件下，建立了计及其励磁调节特性影响的短路电流计算模型。在此基础上，基于对称分量法建立了含多双馈风电机组接入的电网各序等效电路，通过对电网电动势方程、故障边界条件方程和双馈风电机组短路计算模型方程进行迭代求解，计算电网各支路的故障电流和各节点电压。与算例的仿真结果对比表明，该短路电流计算方法计算准确度高，可较好地满足工程应用要求。

双馈风电机组短路计算低电压穿越等效模型迭代计算

0　引言

电网短路电流计算是继电保护整定计算、电网运行控制和设备选型的重要基础。近年来，为了减少对化石能源的过度消耗，实现经济、社会、生态的协调可持续发展，风力发电技术得到了广泛应用。风电机组规模化接入电力系统后，由于其馈出的短路电流特性与传统交流电机存在较大差异，因此，以交流同步电机供电电源为基础的传统电网故障分析方法已不能满足含风电电源的电网短路计算的要求，这已成为当前亟待解决的重要问题。

风电机组根据其基本工作原理，可分为双馈型风电机组（Doubly-Fed Induction Generators，DFIG）和直驱式风电机组两种基本类型，后者由于通过逆变器与电网互联，故也可称为逆变型电源（Inverter Interfaced Distributed Generator，IIDG）。迄今，国内外学者针对风电机组故障特性和短路电流计算方法开展了多方面的研究工作。在逆变型电源分析方面，文献［1］根据正常并网运行控制策略，将IIDG划分为不同类型节点，利用前推回推故障分析方法求取各IIDG故障电流。文献［2］针对含IIDG的复杂配电网，考虑了各IIDG间的耦合，提出了含IIDG的配电网故障分析方法。但逆变型电源的短路电流特性与双馈风电机组存在较大差异，以上分析方法并不适用于含双馈风电机组的电网短路电流计算。

在含双馈风电机组的电网故障特性分析方面，由于DFIG本体撬棒保护的动作行为对其馈出的短路电流特性有较大影响，因此，相关研究从考虑DFIG撬棒保护动作和计及DFIG励磁调节特性影响两方面分别展开。文献［3］采用空间矢量方法推导了电网发生三相短路且撬棒保护动作后，DFIG的短路电流解析表达式，并与普通异步电去动机模型进行了对比分析。文献［4］基于对普通感应发电机短路电流的分析，给出了DFIG最大短路电流的计算方法，并分析了撬棒电阻的阻值对短路电流的影响。文献［5，6］提出了改进的低电压穿越控制策略，在考虑DFIG提供无功支撑的条件下，实现DFIG的不脱网运行。文献［7，8］对不同机端电压跌落情况下DFIG的故障过程进行了研究，但其重点针对的是转子电流的故障特性分析。文献［9，10］将DFIG等效为电压源和阻抗串联的模型，对电网进行故障分析研究，但这种简化等效有待商榷，可能产生较大误差。综上所述，虽然针对双馈风电机组故障特性开展了多方面的研究工作，但主要是针对三相对称短路，或假设撬棒保护动作的这种简单故障形式，没有考虑更为复杂的不对称短路情况以及DFIG低压穿越运行控制策略的影响。此外，如何建立含双馈风电机组的电网短路电流计算模型也是当前亟待解决的重要问题。

本文根据DFIG低电压穿越运行控制策略的技术特点，针对三相对称故障和不对称短路故障，分别建立了计及DFIG励磁调节特性影响的短路计算等效模型；在此基础上，提出了一种通过对电网节点电压方程、故障边界条件方程和双馈风电机组短路计算模型方程进行迭代求解的电网短路电流计算方法，以实现对含多双馈风电机组接入的电网故障分析研究。最后，通过仿真算例，验证了所提出的短路计算方法的可靠性。

1　DFIG低电压穿越控制策略

为了防止在故障期间风电机组大规模脱网事故的发生，国家电网公司在并网规范中已明确要求风电机组在电网短时电压跌落情况下，如发生短路故障时，需维持并网运行，并向外发出无功功率以帮助电网恢复稳定运行，即要求风电机组具备低电压穿越（Low Voltage Ride Through，LVRT）能力［5，11，12］。对 DFIG来说，当电压跌落严重（如机端发生短路），撬棒保护将动作，以保证机组运行安全，此时DFIG可近似用异步电动机模型等效，其短路计算较为简单。但对于大多数电网故障，撬棒保护并不动作，DFIG的励磁调节特性将直接影响其馈出的短路电流特性，使得电网短路计算复杂化，导致传统故障分析方法难以适应含DFIG的电网短路电流计算需求。

为了实现DFIG在电网故障期间的低压穿越运行，学者们提出了多种励磁控制策略和方案，除满足无功要求外，其重点是降低电网不对称故障可能对机组运行带来的危害，典型控制策略包括平衡的定子电流控制策略、平衡的DFIG转子电流控制策略和恒定的转矩控制策略等［11，12］。其中，平衡的DFIG定子电流控制策略可通过控制定子负序电流的方式，有效解决定子负序电流可能造成机组铁心和绕组过热以及机组振动等问题，本文以此为例，对DFIG的低电压穿越过程进行研究分析。

平衡的DFIG定子电流控制策略框图如图1所示。

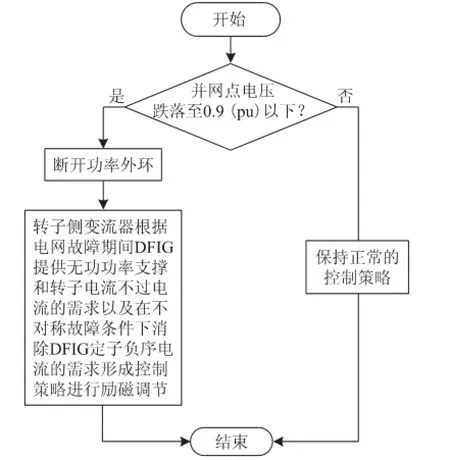
图1　DFIG低电压穿越励磁控制策略框图Fig.1　Flow chart of LVRT control strategy of DFIG

在电网正常状态下，DFIG采用双闭环控制系统［5，6］，外环为功率环，内环为转子电流环［20-22］。在电网故障条件下，由于DFIG实际上难以实现对真实有功、无功功率的准确测量，因此，一旦检测到故障发生，如电网电压低于0.9（pu）时，可将功率外环闭锁［13］。为了实现对电网故障期间的无功支撑要求［14］，DFIG根据电压跌落幅度对无功指令进行调节［6］，其注入电网的无功电流IT为

式中，λ为机端正序电压分量幅值的标幺值。同时，根据转子绕组电流不越限要求进行有功功率控制。

当电网发生不对称短路时，通过励磁控制策略消除定子电流负序分量［12］，同时，根据式（1）对正序电流进行调节控制，以满足无功支持要求。

以下将基于上述控制策略，建立电网短路故障时DFIG的等效数学模型，并据此提出含DFIG的电网短路电流计算方法。

2　计及励磁调节特性影响的DFIG等效模型

2.1DFIG的数学模型

在不考虑定子磁链二阶及以上高次谐波分量的影响，并忽略磁饱和现象的条件下［15］，定子侧采用发电机惯例、转子侧采用电动机惯例，正、反转dq坐标系下的DFIG定子电压和磁链方程分别为

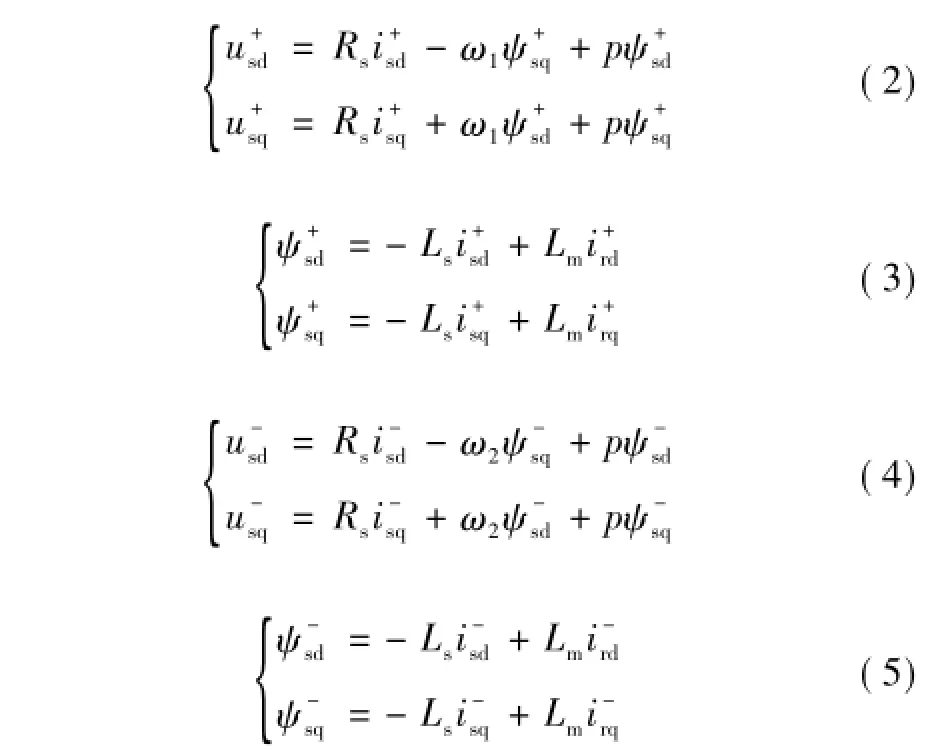
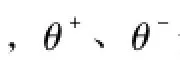
图2　正、反转dq坐标矢量示意图Fig.2　Vector diagram in the positive and negative synchronous reference frames

2.2对称故障时DFIG等效模型

在电网对称故障条件下，DFIG馈入电网的电流中不含负序分量。同时DFIG的功率外环被闭锁，因此只需对正转dq坐标系中转子电流指令值进行控制设计。在定子电压定向的矢量控制技术条件下，正转同步旋转坐标系的d轴分量定向于定子电压矢量Uf，有

式中，Uf为对称电压跌落后的机端电压幅值。联立式（2）、式（3），并在忽略定子电阻的条件下，可得

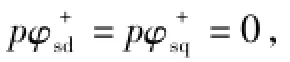
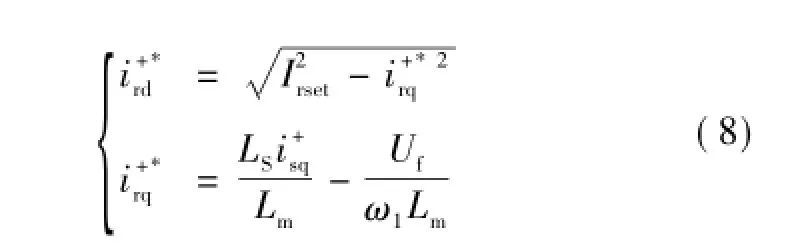
同时，文献［16］表明无论转子侧内环控制器设计成典型Ⅰ型或Ⅱ型系统，在故障情况下，转子电流在同步旋转坐标系中的d轴和q轴分量分别为

由于同步旋转坐标系中的交流分量在三相静止坐标系中为直流分量。因此，不计DFIG定子磁链在同步旋转dq坐标系中衰减的交流分量，联立式（7）～式（9）可得正转同步坐标系下定子故障电流d轴分量和q轴分量分别为

由式（10）可知，DFIG在对称故障条件下的基频电流输出特性由机端电压Uf决定。由于对称故障条件下，DFIG的定子电流负序分量为零，因此可将电网对称故障条件下的DFIG等效为受控的正序电流源模型IDG=IDG∠γDG。

在式（11）中引入θu的主要原因是，θI表征的是IDG与旋转坐标系d轴的夹角，采用定子电压定向矢量控制时，d轴与Uf同相，因此γDG=θI+θu才能正确反映电流IDG与统一参考矢量间的夹角。

2.3不对称故障时DFIG等效模型

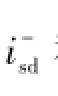
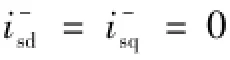
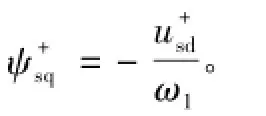
为保证转子电流不过流，假设在电网故障期间转子电流限定值为Irset，联立式（13）和式（14）可得正转坐标系下转子电流d轴分量参考值为

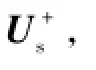
与对称故障时类似，在定子电压定向控制条件下，根据DFIG定子电压在正、反转坐标系下的d轴分量及转子电流参考值代入式（2）～式（5），求解DFIG定子电流d轴分量和q轴分量在不对称故障条件下的稳态分量分别为

由式（17）可知，电网不对称故障条件下定子电流负序稳态分量为零，因此，电网发生不对称故障时，DFIG仍可等效为受控的正序电流源，即有 IDG= IDG∠γDG。

3　含DFIG的电网故障分析

由以上分析可知，考虑励磁调节特性的影响后，DFIG并不能简单等效为电压源和阻抗串联的形式，其等效计算模型为受控正序电流源，且正序输出电流与机端电压有关，特别是不对称故障条件下，DFIG的输出电流还与机端电压在反转同步旋转坐标系下的d轴分量有关，因此，传统的电网故障计算方法不能直接应用，需建立新的计算方法。

在传统电网故障计算中，广泛采用对称分量法以简化计算［18］，即首先建立各序等效电路，得到各序节点电压方程，然后与故障边界条件方程联立求解，完成故障计算。DFIGs接入电网后，给故障计算带来的直接影响是其电源等效模型发生了变化，而电网其他部分仍保持不变，因此，只需将DFIGs电源模型用受控正序电流源代替，仍可沿用上述对称分量法进行故障计算，以下给出基本计算方法和流程。

1）建立各序等效电路及各序节点电压方程

由前述分析知，通过采用合理的低压穿越运行控制策略，无论是对称还是不对称短路，DFIGs均可等效为受控的正序电流源。因此，建立含多DFIG的电网各序等效电路时，在正序电网中，DFIG可用受控注入电流源表征，而传统同步发电机可用恒定注入电流源与次暂态电抗并联模型等效。对于负序和零序网络，各DFIG均可做开路处理，其他部分与传统处理方式相同。

根据所建立的各序等效电路，进一步可得到各序网络的节点电压方程。

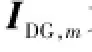
负序和零序节点电压方程为

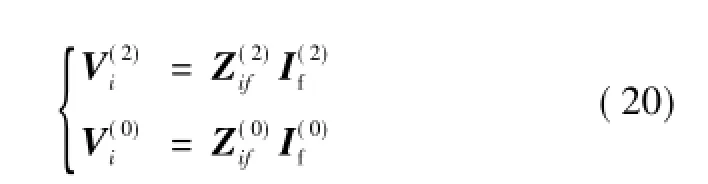
2）建立故障边界条件方程

电网故障类型包括三相对称故障和不对称故障。根据电网不同故障类型和相别可建立故障点边界条件方程［19］。以两相金属性短路为例，其基准相（特殊相）的故障边界条件方程为

其余故障情况下的故障边界条件方程与传统方法相同，具体略。

3）基于迭代方法的电网短路计算

含多DFIG的电网故障计算方法的基本原则与传统方法类同，即可将各序节点电动势方程与故障边界条件方程联合求解，计算各节点的各序电压以及各支路的各序电流，将各序电压和各序支路电流叠加，即可得到各节点和各支路的实际电压和电流。但需要指出的是，由于DFIG为受控电流源，其大小和相位与DFIG接入节点的电压有关，同时，由式（12）和式（19）可以看出，DFIG受控电流源与接入节点电压存在复杂的非线性关系，因此，难以像传统方法一样直接通过解析方法进行求解。

解决上述问题的一种可行方法是采用迭代法进行计算，具体步骤如下:

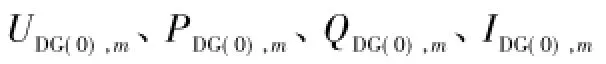
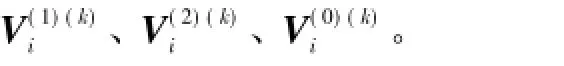
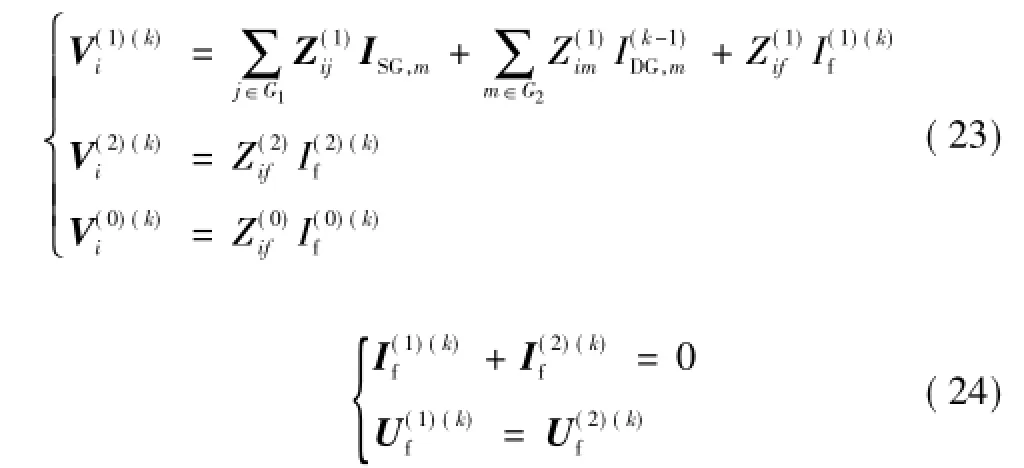
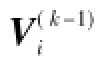
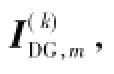
5）根据所计算的各节点各序电压和已知的各序支路阻抗，计算各支路各序电流。

图3　含DFIGs的电网短路计算流程框图Fig.3　Diagram of short-circuit current calculation method in power grid with DFIGs

4　仿真验证

以图4所示的电网为例，在PSCAD中建立其仿真模型。同时，通过MATLAB编写了本文所提出的含DFIGs的电网短路电流计算程序。分别假设电网中节点f发生三相对称短路和不对称短路，将仿真结果与短路电流计算程序输出结果进行对比分析，以验证所提电网故障计算新方法的可靠性。

图4　含DFIGs的简单电网结构示意图Fig.4　Power system with penetration of DFIGs

在图4中，假设各输电线路的型号相同，单位长度线路参数为:r（1）=r（2）=0.17 Ω/km，x（1）=x（2）= 0.394 Ω/km，线路L1、L2、L3、L4和L5的长度分别为5 km、6 km、10 km、5 km和5 km。两绕组变压器T1和T2的容量为均1.6 MV·A，变电压比为0.69/110 kV，联结组别为Yd，漏电抗为6.22%。负荷1和负荷2的等效阻抗均为120+j39.11 Ω，负荷3的等效阻抗为80+j26.08 Ω。系统等效电动势为110 kV，接入电网的两台DFIG的容量均为1.5 MW，额定线电压为690 V，定子漏电抗为0.124 5（pu），转子漏电抗为0.124 5（pu），定转子互感为2.176 7（pu），转子额定转速为1.2（pu），转子电流过电流控制值 Irset为1.2（pu），误差门槛值ε为0.001。

4.1三相对称故障

在f点发生三相对称故障情况下，DFIGs馈出的故障电流和各支路故障电流的理论计算值和仿真实测值对比如表1所示。DFIGs机端电压和各节点电压的理论计算值和仿真实测值如表2所示。当测量值的幅值为0时，表中∠-表示该量的角度无意义。

由表1可知，在电网发生对称故障条件下，本文所提电网故障分析方法计算的电流幅值理论值与仿真值之间的最大误差为0.738%，最大电流相角误差为1.1°。由表2可知，本文所提方法计算的节点电压幅值偏差为0.58%，电压相角最大误差为1.44°。因此，在电网发生对称故障时，本文所提方法具有较高计算准确度。

4.2不对称故障

表3和表4中分别给出了f点发生BC两相短路时的电流和电压对比结果示例。由表3和表4可知，在电网发生不对称故障条件下，DFIG输出电流的理论值和仿真值中均不含负序分量，证明了计及励磁调节特性影响后，DFIG可等效为受控正序电流源。同时，本文所提故障计算方法的输出结果与仿真测量结果的幅值误差和相位误差均较小，验证了故障计算新方法的可靠性。

4.3算法收敛性和计算速率分析

本文中提出的短路电流迭代计算方法主要涉及电网节点电压方程的迭代计算，其系数矩阵为节点阻抗矩阵，由于实际电网中的电抗值远大于电阻值，其节点阻抗矩阵可近似视为对称正定矩阵，因此，迭代算法一般具有良好的收敛性。为了进一步验证故障迭代算法的性能，以含风电场接入的某省实际电网为例，分析不同电网规模和不同DFIG接入台数对算法计算速率和收敛性的影响。

表1　对称故障条件下电网短路电流比较Tab.1　Branch currents under three-phase fault occurs at f（单位:kA）

表2　对称故障条件下电网节点电压比较Tab.2　Node voltages under three-phase fault occurs at f（单位:kV）

表3　BC两相相间故障下电网短路电流比较Tab.3　Branch currents on condition that two-phase fault occurs at f（单位:kA）

表4　BC两相相间故障下电网节点电压比较Tab.4　Node voltages on condition that two-phase fault occurs at f（单位:kV）

根据某省实际电网风电场的接入位置，对电网进行等效化简，可得到包括31个节点，含5个电源节点和2个风电场节点的简化等效网络，如图5所示。其中，风电场同一集电线上相同型号的DFIG进行等效处理，可简化为每个风电场接入4台等效的双馈风电机组。在仿真计算中，分别考虑风电场所有机组均投入运行及每个风电场只投一组双馈风电机组运行两种方式。仿真结果表明，在各类故障情况下，本文提出的迭代算法均能可靠收敛。仿真结果同时显示，电网规模和接入双馈风电机组台数对迭代算法的迭代次数和计算速度有一定影响，表5中给出了算法迭代次数和计算速度的测试结果示例，并与图4所示的简单系统的仿真情况进行了对比。其中，测试环境为Windows 7操作系统、Intel（R）Core（TM）i5 CPU 2.9 GHZ和4GB RAM，对应的故障计算条件为图4和图5中f1处发生两相相间短路。

图5　含风电场接入的某区域电网示意图Fig.5　Region power system with wind farms

表5　电网规模和DFIG接入台数对迭代算法性能的影响Tab.5　Performance of the iteration algorithm under different power system and DFIGs condition

由表5可知，电网规模的扩大和双馈风电机组接入台数的增多均会导致迭代算法的计算时间和迭代次数增加，但算法仍具有较快的计算速度，特别是在实际工程应用中，风电场对电网的影响一般主要局限于风电场接入点附近的局部区域电网，电网计算规模有限，因此，本文提出的含双馈风电机组接入的电网短路电流迭代计算方法可较好满足实际应用要求。

5　结论

双馈风电机组馈出的短路电流特性与交流同步电机存在较大差异，这使得以交流同步电机供电电源为基础的传统电网故障分析方法不能直接应用于含双馈电源的电网短路计算。本文以控制定子负序电流的DFIG低电压穿越控制策略为例，建立了计及DFIG励磁调节特性影响的短路计算等效模型。研究表明，无论是对称短路还是不对称短路，DFIG均可用正序受控电流源表征，而不包含负序和零序电流分量。由于受控电流源的大小和相位与DFIG接入节点的电压存在复杂的非线性关系，因此，难以直接通过解析方法进行求解。针对此问题，提出了一种通过对电网节点电压方程、故障边界条件方程和双馈风电机组短路计算模型方程进行迭代求解的电网短路故障计算新方法。仿真结果表明，该方法不仅计算速度快，且计算准确度高，可较好满足含大规模双馈风电机组接入的电网短路计算和保护整定计算的应用要求。

对于采用其他控制策略的双馈风电机组，本文所提出的电网故障计算方法也同样适用，只是需对机组短路计算模型进行调整。

［1］王守相，江兴月，王成山.含分布式电源的配电网故障分析叠加法［J］.电力系统自动化，2008，32（5）: 38-42. Wang Shouxiang，Jiang Xingyue，Wang Chengshan.A superposition method of fault analysis for distribution systems containing distributed generations［J］.Automation of Electric Power Systems，2008，32（5）:38-42.

［2］吴争荣，王钢，李海锋，等.含分布式电源配电网的相间短路故障分析［J］.中国电机工程学报，2013，33（1）:130-136. WuZhengrong，WangGang，LiHaifeng，etal. Analysis on the distribution network with distributed generators under phase-to-phase short-circuit faults［J］. Proceedings of the CSEE，2013，33（1）:130-136.

［3］Sulla F，Svensson J，Samuelsson O.Symmetrical and unsymmetrical short-circuit current of squirrel-cage and doubly-fedinductiongenerators［J］.ElectricPower Systems Research，2011，81（7）:1610-1618.

［4］徐殿国，王伟，陈宁.基于撬棒保护的双馈电机风电场低电压穿越动态特性分析［J］.中国电机工程学报，2010，20（22）:29-36. Xu Dianguo，Wang Wei，Chen Ning.Characteristic analysis of doubly-fed induction generator low voltage ride-throughbasedoncrowbarprotection［J］. Proceedings of the CSEE，2010，20（22）:29-36.

［5］Xiang Dawei，Ran Li，Tavner P J，et al.Control of a doubly fed induction generator in a wind turbine during grid fault ride-through［J］.IEEE Transactions on Energy Conversion，2006，21（3）:652-662.

［6］Lopez J，Gubia E，Olea E，et al.Ride through of wind turbines withdoublyfedinductiongeneratorunder symmetrical voltagedips［J］.IEEETransactionson Industrial Electronics，2009，56（10）:4246-4254.

［7］熊小伏，欧阳金鑫.电网短路时双馈感应发电机转子电流的分析与计算［J］.中国电机工程学报，2012，32（28）:114-121. Xiong Xiaofu，Ouyang Jinxin.Analysis and calculation of rotor currents for doubly-fed induction generators under short circuits in power grids［J］.Proceedings of the CSEE，2012，32（28）:114-121.

［8］Lopez J，Gubia E，Sanchis P，et al.Wind turbines basedondoublyfedinductiongeneratorunder asymmetrical voltage［J］.IEEE Transactions on Energy Conversion，2008，23（1）:321-330.

［9］Kanellos F D，Kabouris J.Wind farms modeling for short-circuit level calculations in large power systems［J］.IEEE Transactions on Power Delivery，2009，24（3）:1687-1695.

［10］ 孙景钌，李永丽，李盛伟，等.含逆变型分布式电源配电网自适应电流速断保护［J］.电力系统自动化，2009，33（14）:71-76. Sun Jingliao，Li Yongli，Li Shengwei，et al.Study on adaptive current instantaneous trip protection scheme for distribution network with inverter interfaced DG［J］. Automation of Electric Power Systems，2009，33（14）: 71-76.

［11］Xu L，Wang Y.Dynamic modeling and control of DFIG based wind turbines under unbalanced network conditions［J］.IEEE Transactions on Power Systems，2007，22（1）:314-323.

［12］ 胡家兵.双馈异步风力发电机系统电网故障穿越（不间断）运行研究——基础理论与关键技术［D］.杭州:浙江大学，2009.

［13］Marques G D，Sousa D M.Understanding the doubly fed induction generator during voltage Dips［J］.IEEE TransactionsonEnergyConversion，2012，27（2）: 421-431.

［14］ 国家电网公司.GB/T 19963—2011风电场接入电力系统技术规定［S］.

［15］Morren J，de Haan S W H.Short-circuit current of wind turbines with doubly fed induction generator［J］.IEEE TransactionsonEnergyConversion，2007，22（1）: 174-180.

［16］Kong Xiangping，Zhang Zhe，Yin Xianggen，et al. Study offaultcurrentcharacteristicsoftheDFIG considering dynamic response of the RSC［J］.IEEE TransactionsonEnergyConversion，2014，29（2）: 278-287.

［17］Lopez J，Sanchis P，Roboam X.Dynamic behavior of the doubly fed induction generator during three-phase voltage dips［J］.IEEE Transactions on Energy Conversion，2007，22（3）:709-717.

［18］Kamh M Z，Iravani R.Unbalanced model and powerflow analysis of microgrids and active distribution systems［J］.IEEE Transactions on Power Delivery，2010，25（4）:2851-2858.

［19］ 何仰赞，温增银.电力系统分析［M］.3版.武汉:华中科技大学出版社，2002.

［20］严干贵，王茂春，穆钢，等.双馈异步风力发电机组联网运行建模及其无功静态调节能力研究［J］.电工技术学报，2008，22（7）:98-104. YanGangui，WangMaochun，MuGang，etal. Modeling of grid-connected doubly-fed induction generator for reactive power static regulation capacity study［J］. Transactions of China Electrotechnical Society，2008，22（7）:98-104.

［21］龚文明，孟岩峰，胡书举，等.一种应用PIR控制器的双馈风力发电机组电流谐波控制方法［J］.电工技术学报［J］.2013，27（9）:95-103. Gong Wenming，Meng Yanfeng，Hu Shuju，et al.A method with PIR controller for the elimination of harmonic currents in a DFIG based wind power system［J］. Transactions of China Electrotechnical Society，2013，27（9）:95-103.

［22］ 贺益康，周鹏.变速恒频双馈异步风力发电系统低电压穿越技术综述［J］.电工技术学报，2009，23（9）:140-146. He Yikang，Zhou Peng.Overview of the low voltage ride-throughtechnologyforvariablespeedconstant frequency doubly fed wind power generation systems［J］. Transactions of China Electrotechnical Society，2009，23（9）:140-146.

The Fault Calculation Method of Power Systems Including Doubly-fed Induction Generators

Xiao Fan1Zhang Zhe1Yin Xianggen1Yang Hang1Yang Zengli2
（1.State Key Laboratory of Advanced Electromagnetic Engineering and Technology Huazhong University of Science and TechnologyWuhan430074China 2.State Grid Hubei Electric Power CompanyWuhan430077China）

The complex fault current characteristics of doubly-fed induction generators（DFIGs）cause that the conventional fault analysis method based on AC synchronous generators is not applicable for the power systems containing DFIGs.According to the low voltage ride through（LVRT）control strategy of the DFIGs，the shortcircuit calculation models of the DFIGs are established considering their excitation regulation characteristics for the three-phase fault or the unbalanced fault.Based on this，the sequence networks of the power systems containing DFIGs are proposed using the symmetrical component method.According to the nodal voltage equations，the fault boundary conditions equation，and the short-circuit calculation models of DFIGs，the branch currents and the node voltages are calculated based on an iterative algorithm.The simulation results show that the proposed method has a high accuracy of short-circuit current calculation and can meet the requirements of engineering applications.

DFIGs，short-circuit calculation，low voltage ride through，equivalent model；iterative algorithm

TM74

国家自然科学基金（51177058、51277084）资助项目。2015-01-20改稿日期 2015-05-04

肖繁男，1989年生，博士研究生，研究方向为含分布式电源接入的智能配电网继电保护与通信技术等。

E-mail:xiao103fan@163.com（通信作者）

张哲男，1962年生，博士，教授，研究方向为电力系统继电保护，新能源及超导技术等。

E-mail:zz_mail2002@163.com