某线膛火炮战斗部发射强度数值模拟

徐赫阳，乔相信，郭克强，李文浩，彭琳茜

(沈阳理工大学 装备工程学院，沈阳 110159)



某线膛火炮战斗部发射强度数值模拟

徐赫阳，乔相信，郭克强，李文浩，彭琳茜

(沈阳理工大学 装备工程学院，沈阳 110159)

为研究某新型战斗部的发射强度，采用LS-DYNA软件建立战斗部在膛内运动模型，对该模型进行了发射强度仿真和分析，得到了战斗部在不同运动阶段的应力、应变曲线。分析第一、第二临界状态时战斗部的应力、应变值及相应强度准则，并进行了实验验证，模拟结果与实弹实验结果基本吻合。结果表明，战斗部实验和数值模拟结果均满足其强度条件，模拟数据可为其结构改进和同类战斗部强度分析提供参考。

弹药工程；发射强度；数值模拟

弹丸在发射过程中沿炮膛运动，在多种复杂载荷的共同作用下，会使战斗部壳体材料产生应力和变形。如果战斗部的变形超过其许用限度，会影响战斗部在膛内的正常运动，甚至造成弹体破裂、发生膛炸。为保证战斗部发射的安全性，在战斗部结构设计时均需要对其进行强度分析。

前苏联学者曾提出一种确定弹带压力的方法，但由于不能直接计算而不被广泛使用。布林克方法将弹体简化为无限长厚壁圆筒[1]，能有效校核结构相对简单的圆柱部及定心部区域。国内学者也做了大量的研究工作，并给出相关的工程近似公式。但由于战斗部结构的不规则性和载荷的复杂性，且允许出现一定程度的塑性变形，使得弹丸强度分析大多停留在实弹射击实验的基础上，常规方法无法很好的解答[2]。

本文借助有限元软件对战斗部膛内运动过程进行分析研究，校核其结构强度，并进行了实验验证，为该弹的改进和研发提供参考。

1　载荷及失效分析[1]

1.1载荷分析

弹丸在发射过程中载荷主要有：火药气体压力、弹带压力、导转侧力、惯性力、装填物压力、摩擦力、不均衡力等。其中火药气体压力是最主要载荷，是推动弹丸在膛内运动的主要因素，对于线膛炮所配用的旋转稳定弹，由于有弹带的密封作用，火药气体几乎完全作用在弹带后部的弹尾部，对弹尾部的结构强度有很大影响。其计算公式：

(1)

式中：P为炮膛压力；φ为次要功系数；mω为发射药质量；m为弹丸质量。

1.2临界状态

弹丸的发射过程将面临三个危险临界状态。

第一临界状态，即弹带完全嵌入身管膛线时。弹带区在径向压力的作用下径向压缩变形，除弹带区域，其它区域的应力、应变值均较小。弹带区变形如图1所示。

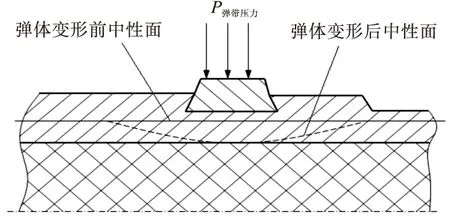
图1　第一临界状态弹体变形示意图

第二临界状态，即膛内压力达到最大时。此时弹底压力值、轴向过载达到峰值；弹底由于火药气体的作用产生凹陷变形，弹尾部和弹带区产生径向压缩变形。在轴向惯性力作用下，弹丸头部和圆柱部将产生轴向墩粗、径向膨胀变形。弹体变形如图2所示。

图2　第二临界状态弹体变形示意图

弹丸第三临界状态，即弹丸完全脱离炮口时。由于大部分载荷突然卸载，使弹体材料因弹性恢复而发生震颤。因此对于抗拉强度大大低于抗压强度的脆性材料，必须考虑该状态对弹体强度的影响。文中的壳体材料为35CrMnSiA钢，有较好的韧性和抗拉性，故数值模拟时忽略该状态对弹丸的影响。

1.3失效准则

1)应力准则

强度条件为：σ<[σ0]

式中：σ为材料所受应力；[σ0]为材料的许用应力。

2)应变准则

强度条件为：2W*<[2W*]

式中：W*为材料的残余变形量；[2W*]为允许的材料残余变形量。

根据文献[1]，弹体材料的残余变形许用值如表1所示。

表1　弹体残余变形许用量

2　数值模拟

2.1物理模型

战斗部的结构如图3所示，由引信、头螺、含能破片、弹丸壳体、推板、抛射药、炸药等组成。考虑战斗部零部件的高度轴对称特性，实际计算时采用1/4模型，cm-g-μs单位制。

图3　战斗部结构和火炮身管模型

2.2数值模型[3]

战斗部各零部件及火炮身管均采用Lagrange算法。在战斗部挤进过程中，身管材料变形量很小，可以忽略不计，将其简化为刚性材料。参数分别为ρ=7.83g/cm3、E=210GPa、μ=0.3。

抛射药和炸药采用Elastic材料模型描述。弹丸引信、头螺、含能破片壳体、含能材料、弹丸壳体和推板均采用Plastic-Kinematic材料模型，应力应变关系为

σy=[1+(ε/C)-q](σ0+βEεeff)

(2)

式中：ε为应变率；εeff为有效塑性应变；σ0、E、C为材料参数，表征材料敏感率特征。具体参数值见表2，未列出参数采用软件自带缺省值或忽略。

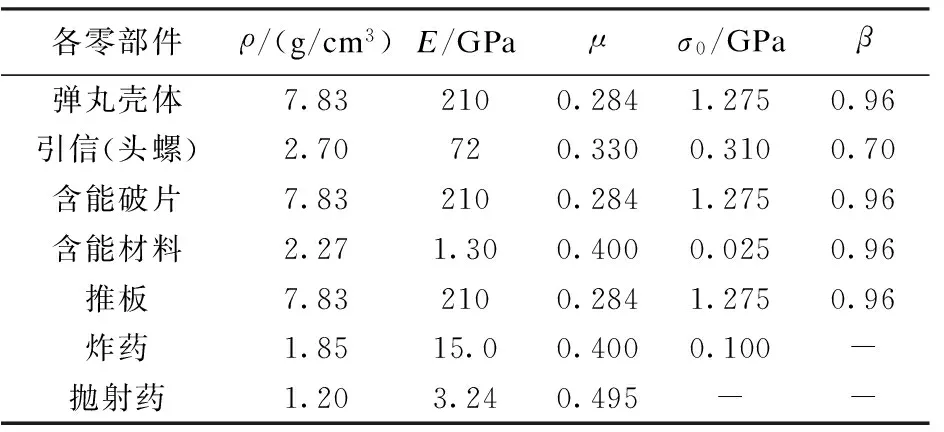
表2　各材料性能参数[4-5]

针对战斗部的前后弹带，考虑到其在随弹丸一同挤进身管膛线过程中会出现高强度、高应变、高应变率的特征，采用Johnson-Cook材料模型和Gruneisen状态方程描述。Johnson-Cook模型的基本公式为

(3)

表3　弹带材料性能参数[4-5]

2.3数值模拟结果及分析

图4和图5分别给出了上弹带完全挤进膛线和膛内压力最大时刻的等效应力分布云图，由于篇幅所限，其它时刻的等效应力云图不再列出。

图4　应力分布(弹带完全挤入)

图5　应力分布(膛压最大)

从计算结果来看，随着弹带不断挤进膛线，膛线对弹带的压力不断增大，弹带凹槽区域的应力随之增大，应力波由弹带凹槽处向两侧传播，当上弹带完全挤进膛线时，最大应力可达到1382MPa，出现在弹带凹槽处顶端。与此同时，弹带与弹体的塑性应变也不断增大，弹带最大塑性应变为0.284mm，出现在弹带顶部。

1931年9月，但采尔如约来到南京的中研院，带来民族学标本134种，另外还有图标120幅、各族照片28幅。民族博物馆建设，因经费等各种原因耽搁下来，最终未能实现。为充分利用但采尔带来的这些物品，蔡元培就专门指示在中研院辟出地方，设立了一个民族学标本陈列室。远道而来的但采尔便留在中研院民族学组从事民族学研究。

随着弹体的不断运动，上、下弹带全部进入膛线，由挤压弹带而引起的径向应力开始减弱，弹丸加速度逐渐增大，由火药推力引起的轴向惯性力开始占据主导，在2700～3000μs时间内达到最大。弹丸顶部的含能破片及推板与弹体的接触应力不断增加，含能破片区域有明显的传向弹底的应力波，最大应力为481MPa，出现在梅花形推板和弹体接触区域。而弹体由于出现应力集中点，最大应力达到995MPa，除应力集中点外其它主要受力部位应力在400～600MPa之间，最大应力出现在弹底靠近弹腔区域。

由于该战斗部结构较为复杂，为更精确分析壳体强度，了解各区域的应力、应变分布情况，在弹丸壳体壁厚突变和应力集中处选取7个观察点，如图6所示，并提取发射过程中相应单元的应力、应变时间历程曲线，如图7和图8所示。

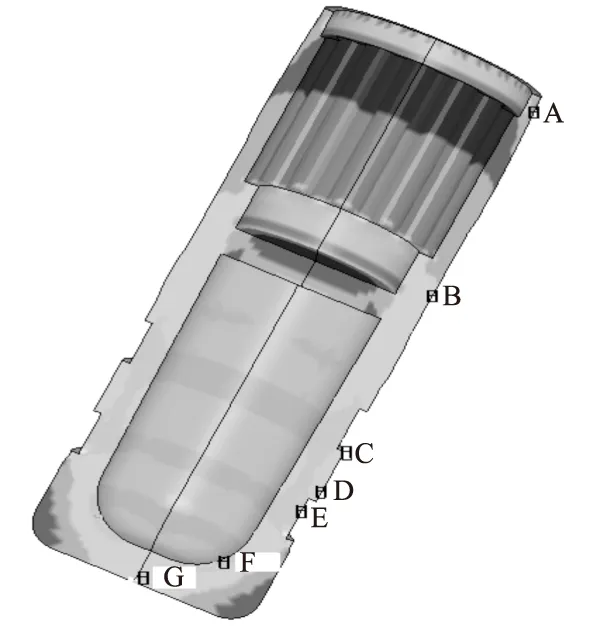
图6　战斗部壳体观察点单元

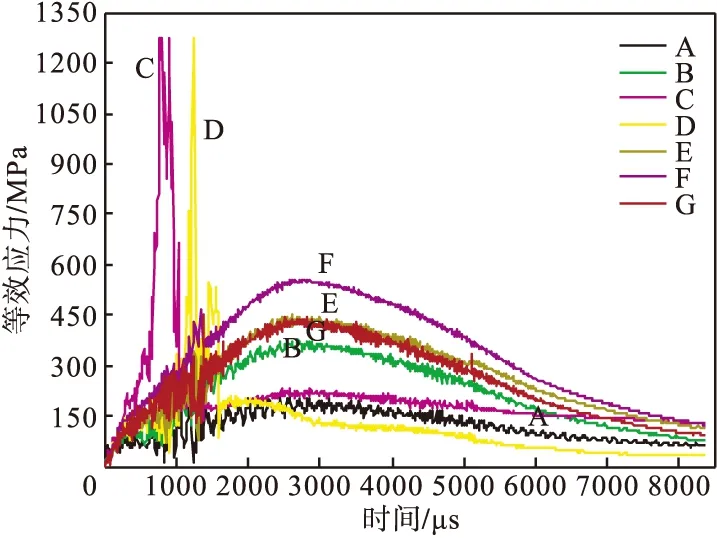
图7　应力曲线

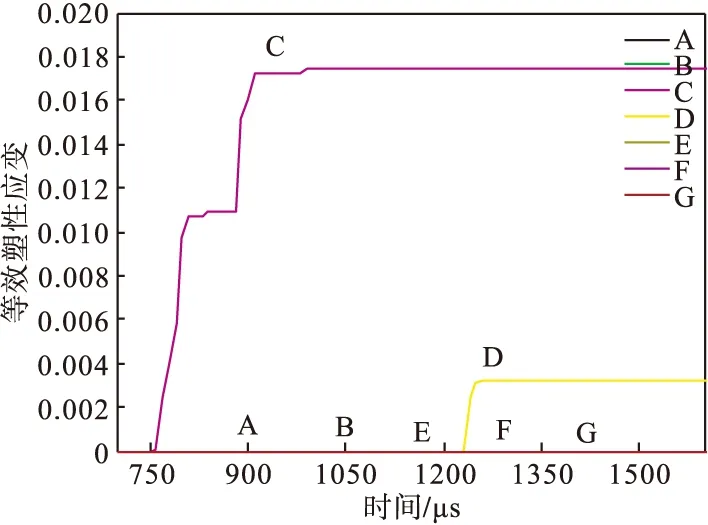
图8　塑性应变曲线

由图7和图8可以看出，900～1200μs弹丸上、下弹带相继挤进膛线，面临第一临界状态。弹带凹槽中间处单元E应力出现轻微波动，其最大应力远小于材料屈服强度(1275MPa)，未发生塑性变形。单元C、D应力值出现剧烈波动，其峰值高于壳体材料屈服强度，分别出现了0.0178mm和0.0032mm的轻微变形。在弹丸实际加工过程中，各棱角处会采用工艺倒角以避免此类因应力集中现象而导致的变形，因此可以忽略其变形，即弹丸未发生变形。

2850μs时，膛压值达到最大，面临第二临界状态。壳体壁厚突变处单元A、B和弹底拐角及弹底中心处单元F、G的应力值均随弹丸轴向惯性力的增大而增大，并达到各自峰值，但以上单元的应力峰值均低于其屈服强度，处于线弹性阶段。

3　实验验证

为验证数值模拟结果正确性，进行了弹丸强度实验。弹丸配阻力引信，其结构如图9所示。

图9　实验弹丸

以339.7MPa膛压，采用某型弹道炮进行强装药试射，实验射击数量共2发。选定弹体上5个特殊位置，测量弹丸各位置发射前后的尺寸，结果如表4所示。

表4　射击前后尺寸　mm

由表4可以看出，两发弹丸在射击前后各部位变形量均为0，即弹丸在射击过程中壳体结构未发生塑性变形，与模拟仿真结果相吻合。

4　结论

(1)弹丸在膛内运动过程中，第一临界状态时，由于并未对几何模型进行倒角，致使弹带凹槽顶部出现应力集中现象，局部应力达到1382MPa，超过材料屈服应力1275MPa，排除该因素影响，弹丸各部位均未发生变形。第二临界状态时弹体最大应力出现在弹底及靠近弹腔附近区域，其最大应力值为573MPa，小于屈服应力，处于弹性变形阶段。

(2)实验结果表明弹体各部位均未发生塑性变形，模拟所得相关数据符合实际情况，证明该仿真模型较为合理，可以作为同类弹丸设计参考。

[1]魏惠之，朱鹤松，汪东晖，等.弹丸设计理论[M].北京：国防工业出版社，1985：43-47.

[2]卜仕彪.复合增程榴弹第一临界状态动力学模型计算分析[D].南京：南京理工大学，2006：4-11.

[3]李裕春，时党勇.ANSYS10.0/LS-DYNA基础理论与工程实践[M].北京：中国水利水电出版社，2006.

[4]米粮川，高树滋，赖长缨.内弹道挤进过程仿真研究[J].弹箭与制导学报，2012,32(1)：133-135.

[5]赵晓宁，何勇，张先锋，等.A3钢抗高速杆弹侵彻的数值模拟与实验研究[J].北京理工大学学报，2011，35(2)：165-166.

(责任编辑：赵丽琴)

The Numerical Simulation of Launching Intensity for Rifled Gun Warhead

XU Heyang，QIAO Xiangxin，GUO Keqiang，LI Wenhao，PENG Linxi

(Shenyang Ligong University，Shenyang 110159，China)

To study the launching intensity of a new warhead,LS-DYNA software is used to develop the motion model of warhead in the bore,using the software to make the launching intensity simulation and analysis for the model to get the stress and strain curve of warhead in the different stages of exercise,and to analyze the stress and strain data when the warhead is in the first and the second critical state and the corresponding value of the strength criterion,and to have a test.Simulation results with actual firing test results are basically consistent.The results show that the results of numerical simulation and experiment can meet the requirements of practical application,and the simulation data can provide reference for the structural improvement and the strength analysis of the same kind of warhead.

ammunition engineering；launching intensity；numerical simulation

2015-12-29

徐赫阳(1992—)，男，硕士研究生；通讯作者：乔相信(1959—)，男，教授，研究方向：弹药工程与爆炸技术。

TJ430

A