电磁感应教学中一个容易忽视的问题
金 红
(武汉市黄陂区第一中学 湖北 武汉 430300)
电磁感应教学中一个容易忽视的问题
金 红
(武汉市黄陂区第一中学湖北 武汉430300)
以一题为例,分析了电磁感应“切割情形”中,若同时伴有因磁场随时间变化导致的感生电动势作用,安培力所做功的值与回路产生的焦耳热不等的原因.
安培力做功 焦耳热 感生电动势
对电磁感应“切割情形”中的能量转化问题,我们常告诉学生:安培力做负功将有机械能转化为电能,安培力做正功电能将转化为机械能,而在纯电阻电路中电能会全部转化为焦耳热.安培力若做负功,可用回路中产生的焦耳热等量替代.学生们用该结论解题也屡试不爽,殊不知这些结论使用都有一定的条件限制.以下题第(3)问的解答为例说明其中的原因.
【例题】如图1所示,两平行金属导轨MN,PQ固定在绝缘水平面上,两导轨之间距离L=1 m,图中MP,AB,CD,EF之间的距离也均为L=1 m,导轨MN,PQ和连接线MP单位长度电阻均为R0=0.1 Ω,虚线AB右侧空间存在匀强磁场,方向竖直向下,且磁感应强度大小随时间的变化关系为Bt=(0.2+0.1t) T,导体棒开始时在外力作用下静止于CD处,若导体棒的电阻不计,求:
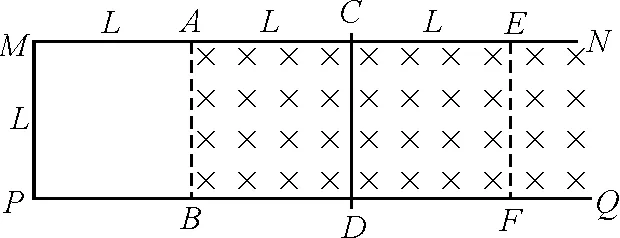
图1
(1)通过导体棒的电流大小和方向;
(2)若导体棒在外力作用下以2 m/s的速度匀速向右运动,在t=0时刻刚好经过CD处,则此时导体棒所受的安培力为多大;
(3)在第(2)问的情境下,导体棒从CD匀速运动到EF的过程中安培力做的功为多少.
分析与探讨:(1)、(2)略.
(3)t时刻穿过回路的磁通量
Φ=BtSt
式中
Bt=(0.2+0.1t) T
St=L(L+vt)=(1+2t) m2
根据法拉第电磁感应定律
t时刻回路中的感应电动势为
即
Et=(0.5+0.4t) V
t时刻回路的总电阻为
Rt=5LR0+2vtR0=(0.5+0.4t) Ω
故t时刻通过导体棒的电流为
即回路电流不随时间变化,为定值.
导体棒所受安培力大小
F安=BtIL=(0.2+0.1t) N
即安培力与时间呈线性关系;而导体棒匀速运动,故安培力与位移s关系为
也是线性关系,则由F安-s图线所围“面积”得安培力所做的功为
有学生根据能量转化关系,认为
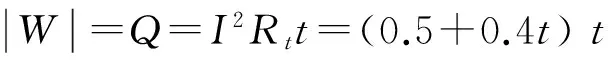
其实是没有弄清楚安培力做负功把机械能转化为电能的机理条件与过程.在只有动生电动势的情景中,非静电力为洛伦兹力的一个分力,在导体棒切割运动中,垂直于棒方向上的洛伦兹力分力的宏观效应即为安培力,对棒做负功使得棒的动能减少,沿棒方向上的洛伦兹力分力即为非静电力,对电荷做正功.由于洛伦兹力总不做功,所以安培力做负功的数值与非静电力做正功的数值相等.非静电力做功转化为电能,在纯电阻电路中转化为焦耳热,所以有安培力做的功值等于回路中产生的焦耳热.
本题中,由上面式子
可知,除动生电动势(E1=BtLv)外, 还存在因磁场随时间变化产生的感生电动势,即式中第一项.产生感生电动势的非静电力是感生电场力,不是洛伦兹力沿导体棒的分力.根据楞次定律,本题感生电动势与动生电动势方向相同,感生电场力也做正功,将外界激发磁场的能量转化为电能,也产生焦耳热,故电路中产生的焦耳热应等于安培力所做负功的绝对值与感生电场力所做正功数值之和.我们计算一下感生电场力所做正功提供的能量
W感=E感It=(0.1+0.2t)t
画出P感=E感I随时间t的变化图像,可求出W感=0.075 J,这正是上述两种方法求解的差别.
2015-12-19)

