水库群优化调度模型求解加速策略研究

明　波，黄　强，王义民，刘登峰，管　剑

(西安理工大学 西北旱区生态水利工程国家重点实验室培育基地，陕西 西安 710048)



水库群优化调度模型求解加速策略研究

明波，黄强，王义民，刘登峰，管剑

(西安理工大学 西北旱区生态水利工程国家重点实验室培育基地，陕西 西安 710048)

针对传统水库群调度模型求解计算耗时较长的缺陷，提出了一种计算程序加速策略。通过转变水库调度计算过程中水库特征曲线的插值模式，根据水库特征曲线节点数据预先构造分段线性函数，利用分段函数替换传统插值方法以实现水库特征曲线的读取。以典型入库流量下某梯级水库发电优化调度为实例，选用布谷鸟算法进行优化计算，对比了传统插值策略与加速策略。结果表明：基于分段线性函数的加速策略能明显缩短计算耗时，同时该加速策略对算法的收敛性、优化结果以及其稳定性几乎无影响。因此，基于分段线性函数的加速策略合理、可靠，是提高水库调度模型求解效率的一种实用、有效方法。

水库群；优化调度；分段线性函数；加速策略；布谷鸟算法

在气候变化和人类活动共同作用形成的变化环境下，由于水资源的稀缺性以及时空分布不均，导致水资源供需矛盾极为突出，严重制约了地区社会、经济的可持续发展。

水库(群)基于调度规则，对天然径流进行适当调节，以实现人类需求和水文过程的动态协调与匹配。水库调度模型的求解是获取水库(群)调度规则的基础。

库群调度约束条件众多，耦合复杂的水力、电力联系，是一个高维、非凸、非线性的复杂最优控制问题[1]。动态规划(DP)及其变种算法在库群优化调度中最为普遍，但均不同程度地存在“维数灾”、收敛性差、依赖初始解等缺陷。智能算法具有计算效率高、寻优机制简单、鲁棒性强等优点，可避免常规方法的不足，为库群调度提供了一条新途径[2]，如最近提出的云变异人工蜂群算法(CABC)[3]、正态云变异蛙跳算法(NCM-LFLA)[4]、改进布谷鸟算法(ICS)[5-6]等。智能算法的并行搜索机制虽然能够在一定程度上缓解水库调度中的 “维数灾”问题，但其解的稳定性和有效性不足，其最优解与计算耗时之间存在固有的矛盾[7]，可见“维数灾”问题并未在根本上得到有效解决。近年来，不少学者尝试采用多核并行计算[8-11]方式求解水库群调度问题。并行计算方法可充分利用计算机的闲置CPU资源，在确保计算精度的前提下大幅度缩短计算耗时。综上，算法的求解效率和寻优精度一直是水资源调度领域关注的重点和难点，如何在确保计算精度的条件下缩短计算耗时是目前急需解决的问题。

为进一步提高水库调度模型的求解效率，本文对水库调度计算中水库特征曲线的读取方式作了改进，提出了一种计算程序加速策略。将该加速策略应用于某梯级水库优化调度中，并采用搜索性能较强的布谷鸟算法进行求解。实例研究表明，在保证计算精度的前提下，该加速策略可大幅度缩减计算耗时，是提高水库调度模型求解效率的一种实用、有效方法。

1　方法原理

1.1库群发电优化数学模型

水库群联合运行调度，具有库容、水文和电力等多种补偿效益。目前主要有“以水定电”和“以电定水”两种运行方式，对应的优化准则有(兼顾保证出力)梯级发电量最大模型和梯级蓄能最大(或耗水量最小)模型。

以发电为主的梯级水库优化调度一般采用梯级发电量最大模型。其问题描述如下：给定调度期内各水电站及区间来水过程，综合各种约束条件，确定梯级各水电站水库的发电用水过程，使得调度期内整个梯级的发电量最大。

目标函数：

(1)

其中：

Nm,t=kmOm,tHm,t

(2)

约束条件：

1)水量平衡约束

Vm,t+1=Vm,t+(Im,t-Om,t-Dm,t)×Δt

(3)

2)流量平衡约束

Im+1,t=Om,t+qm,t

(4)

3)水位、流量、出力上下限约束

(5)

4)边界条件约束

Zm,1=Zm,b,Zm,T+1=Zm,e

(6)

1.2库群优化调度的布谷鸟算法

布谷鸟搜索算法(Cuckoo Search,CS)是Yang和Deb于2009年提出的一种新的群智能算法。该算法通过模拟布谷鸟的寄生育雏行为以及莱维飞行(Lévy flight)特征以寻求优化问题的最优解。由于CS算法参数少、鲁棒性强、搜索效率高，已被成功应用于各领域。本文结合水库调度问题，对CS算法的基本寻优原理进行阐述，可参考文献[5]。假定以水位作为优化变量，则布谷鸟个体编码方式如下：

(i=1,2,…,Npop,t=1,2,…,Tmax)

(7)

式中：Npop为算法种群规模；Tmax为算法的最大迭代次数(进化代数)；d为优化问题的维数。

同其他智能算法类似，CS算法首先生成初始种群，并采用Lévy flight随机游动以及偏好随机游动两个算子对初始种群进行更新，经过反复迭代，直至满足算法的终止条件时停止。

1)Lévy flight算子：

(8)

L(λ)～u=t-λ,1<λ≤3

(9)

式中：u为概率密度函数；λ为步长控制参数。

2)偏好随机游动算子：

(10)

CS算法通过以上两种方式对个体不断更新，当满足终止准则(一般采用达到最大迭代次数)时停止迭代，并输出最优个体。

采用智能算法求解水库调度问题的核心在于如何处理复杂的约束条件。本文采用罚函数方法处理下泄流量约束以及保证出力约束，可得到适应度函数如下：

(11)

式中：p1和p2分别为惩罚系数。

2　水库群调度模型求解加速策略

水库调度模型求解的计算耗时一直是衡量算法优化性能的一个重要依据。没有一种算法能够在计算耗时和寻优精度两方面均同时达到最优。通常，算法的计算耗时与所求解问题的规模、计算平台、算法复杂度以及程序编写效率等密切相关。本文对传统水库调度中水库特征曲线的插值模式作了改进，提出了基于分段线性函数的水库特征曲线读取方法，通过提高计算程序的编写效率以实现算法加速目的。

2.1加速策略基本原理

传统水库优化调度模型求解时，需要预先读取水库特性曲线(水位-库容曲线，尾水位-下泄流量曲线等)。水库特征曲线以离散点的形式存储在计算机内存之中，当需要获取某个水库特征值时，可根据节点数据进行插值计算以获取所需要的水库特征值。插值的实质是根据节点数据构造两变量间的函数关系，根据该函数关系，输入已知变量，得到未知变量。目前，优化调度计算中以两点线性插值方法最为普遍。以水位-库容曲线为例，根据两节点A(z1,v1)和B(z3,v3)对特征点C(z,v)进行插值，以获取水位值z所对应的库容值v，插值过程如图1所示。

图1　水位库容曲线插值过程示意图Fig.1　Schematic of interpolation process for water level-storage curve

根据节点A和B，构造线性函数v=f(z)以表征实际函数v=g(z)，输入水位值z即可得到实际库容值v的逼近值v′。两点线性插值法的计算公式如下：

(12)

通过分析该过程可知，每次插值计算都需要根据节点数值进行参数估计，由于优化过程需要进行多次插值运算，必将导致大量计算耗时的浪费。由于节点数据已知，可以在优化计算之前便预先确定线性函数v=f(z)的参数值。为此，提出了基于分段线性函数的加速策略，对应水位-库容曲线表达式如式(13)：

(13)

式中：ar、br(r=1,2,3,…,n)均为参数，优化计算之前已经确定，可保留多位有效数字以确保计算精度；zs(s=1,2,3,…,n+1)为输入变量。

相比于传统的插值策略，分段线性函数的优势主要表现在：在获取水库某节点数值时，分段函数法需要预先确定节点数据的函数关系式，优化计算时直接调用分段函数即可，相当于执行公式(13)；而传统插值方法在需要获取节点数值时，相当于执行公式(12)。显然，计算参数比直接调用参数耗时更长，因此，基于分段线性函数的水库特征曲线读取方法的计算耗时更短。同时，由于插值和分段线性函数本质上相同，因而算法的计算精也不会降低。

2.2加速策略效用分析

采用智能算法求解水库优化调度问题，计算耗时与目标函数总评价次数基本成正比。因此，可利用目标函数的计算耗时对比分析加速策略与传统插值策略的耗时关系。通常，目标函数评价次数与算法的迭代次数、种群规模成正比，整个优化计算过程中适应度函数总评价次数为：

Fe=Φ(Npop,Tmax)

(14)

式中：Fe为适应度函数的评价次数；Npop为种群规模；Tmax为总迭代次数；Φ为对应的函数关系。

假定单次优化计算中有n项插值项目，完成单点插值CPU耗时分别为t1,t2,…,tn；而采用分段线性函数策略直接调用相应参数CPU耗时均设定为t0。则适应度函数调用一次可节省的时间为：

(15)

完成整个计算过程，加速策略所节省的时间为：

(16)

根据公式(16)可知，采用智能算法求解梯级水库调度问题时，若采用传统的插值方法，计算耗时会随着算法的种群、优化变量个数以及迭代次数的增加而增大；而采用本文所提出的加速策略，可在一定程度上节省计算耗时。

3　实例研究

3.1计算数据

某梯级水库群包含2座大型水库，均具有调节库容，A水库位于B水库上游，调度期为5月～次年4月，主汛期为7～8月。A水库多年平均入库流量为288 m3/s，A、B水库多年平均区间入流为95 m3/s。选取某平水年径流过程作为模型输入，A入库流量以及A-B区间入流如图2所示。

图2　平水年某梯级入库流量过程Fig.2　The inflows of the normal year for the cascade reservoir

计算过程未考虑水流时滞、水库蒸发及渗漏影响。A、B水库的起调水位分别为350 m、175 m，正常蓄水位分别为400 m、200 m，汛限水位分别为392 m、194 m，装机容量分别为1 600 MW、1 200 MW，保证出力分别为310 MW、187 MW。采用CS算法对调度模型进行求解，算法基于MATLAB平台实现，计算机配置为CPU双核，内存2G，操作系统为Win8。

3.2寻优时间对比

分别采用两点线性插值策略以及分段线性函数策略实现水库特征曲线的读取。计算过程中，水库特征曲线仅考虑水位-库容曲线、尾水位-下泄流量曲线。以B水库水位-库容曲线为例，如图3所示，构造了分段线性函数，基本参数如表1所示。使用两点线性插值法对特定点进行插值，实现方式有两种：其一，从最小值开始寻找，找到z1和z3的位置，进行参数估计并计算v，然后跳出循环，记为插值1；其二，遍历z，根据相邻两节点完成所有的参数估计，找到z1和z3的编号，然后再计算v，记为插值2。显然，插值1的计算效率要高于插值2，为了充分说明分段函数方法的有效性，将上述两种线性插值方法均作为比较对象。同时，为保证模拟结果的准确性，将程序独立运行10次，对寻优时间取平均值。不同种群规模和不同迭代次数算法下，算法的寻优时间对比见表2。

图3　B水库水位-库容曲线Fig.3　The water level-storage curve of reservoir B

根据表2可知，对比两种线性插值方法，基于分段线性函数的水库特征曲线的读取方式可以明显缩短算法寻优时间。相对于插值法1，平均速率比为1.8，相对于插值法2，平均速率比为15.2，大约相当于2核和15核的并行计算效果。同时，对比不同的插值方法也可以看出，插值计算中的参数估计过程对算法寻优时间影响极大，插值法1中每次插值只根据部分节点数据计算相应参数，插值法2中每次插值是根据所有节点数据计算全部参数，导致寻优时间恶化。此外，研究中还发现，插值计算是影响水库调度计算时间长短的一个关键性因素。因此，提高水库调度计算效率，除了结合并行计算外，还可从优化插值算法方面进行改进。

表1　B水库水位-库容曲线分段线性函数参数表

表2　不同策略寻优时间对比

3.3优化结果对比

为验证加速策略的可靠性，本文分别统计了算法在不同种群规模、不同迭代次数下梯级发电量的平均值和标准方差，分别见表3和表4。由于两种线性插值方法的实质相同，因此，只选取了插值法1与分段函数法进行对比。从表3可知，采用传统的插值策略，水库群总发电量约为82.76亿kW·h，而采用分段函数策略发电量约为82.88亿kW·h，发电量增幅为0.15%；表4中发电量的标准差可显示出算法的稳健性，采用传统插值策略与加速策略的标准差均较小，且二者几乎相等，可见加速策略对算法的稳定性并无影响。

综合来看，加速策略对算法的寻优精度几乎无影响，这是由于基于分段线性函数的加速策略只改变水库特征曲线的读取方式，但并没有影响算法的搜索机理所致。

表3　不同策略梯级总发电量对比

表4　不同策略结果稳定性对比

此外，还对比了传统插值策略与加速策略对算法收敛性的影响，不同种群规模下算法收敛性对比如图4所示。由图4可知，当算法种群规模Npop=50时，采用加速策略能够改善算法的收敛性；当种群规模Npop=100时，采用加速策略反而削弱了算法的收敛性；当Npop=150时，算法的收敛性有一定程度的提高，但并不明显。考虑到随机算法的收敛性还与初始种群等随机因素有关，算例中加速策略对于收敛性的改变并未呈现确定的趋势，综合考虑，认为加速策略对算法的收敛性影响不大。

图4　不同策略算法收敛性对比Fig.4　Comparison of the convergence performance for different strategies

3.4调度结果合理性分析

为进一步验证调度结果的合理性，针对不同的策略，选取种群规模Npop=50，迭代次数Tmax=300时梯级发电量最大对应的水位与出力过程作对比，如图5和图6所示。由图5和图6可知，传统插值策略与分段函数策略的水位和出力的变化过程基本一致，且均满足各项约束条件；各水库在汛期迅速抬升水位蓄水，非汛期水位逐渐回落，体现水库“蓄丰补枯”的特点；此外，A水库在枯水期放水对B水库进行补偿调节，使得B水库能维持高水头发电，从而降低水耗增加发电量，可见调度结果也是合理的。

综上，本文采用分段线性函数替换传统水库调度计算中的插值方法，以实现对水库特征曲线的读取，进一步提高了水库调度模型的求解效率。同时，所提出的加速策略对优化算法的寻优精度、收敛性以及优化结果的稳定性几乎无影响，因此，本文所提出的加速策略合理、有效，可为水库调度模型的求解提供一条新的思路。此外，本文所提出的加速策略还具有较强的普适性，只要涉及水库特征曲线的读取，便可以采用该方法进一步提高调度模型的求解速度，非常适合求解大规模的水库调度计算问题。

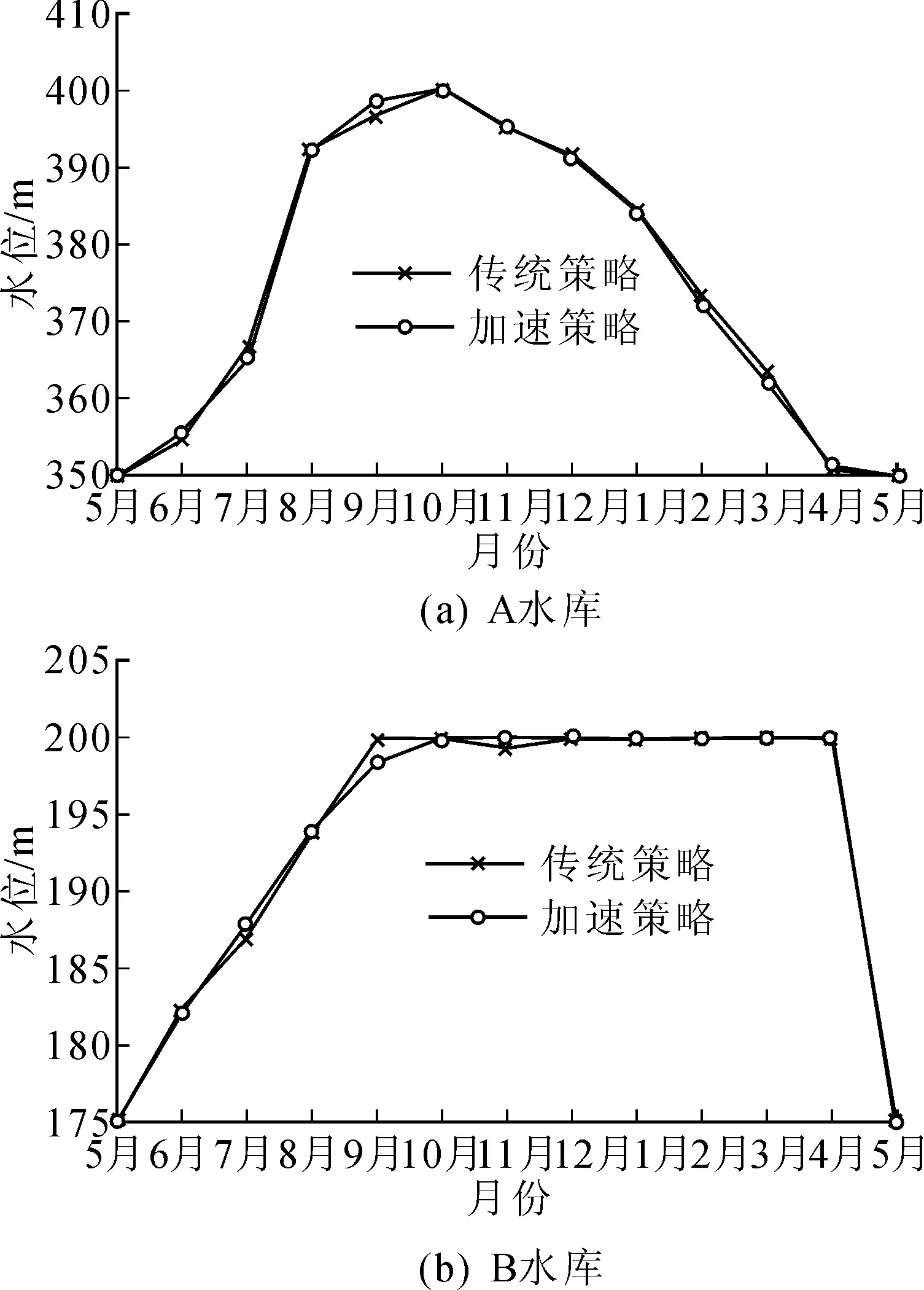
图5　梯级水库水位变化过程对比Fig.5　Comparison of the water level obtained from different strategies

图6　梯级水库出力变化过程对比Fig.6　Comparison of the output obtained from different strategies

4　结　语

梯级水库优化调度模型的求解是水资源调度领域的基础问题和难点问题。本文对传统水库优化调度计算中水库特性曲线的插值方法进行转变，提出了基于分段线性函数表征水库特性曲线的加速策略，实例研究表明：

1)插值计算是影响水库调度计算时间长短的关键性因素，插值方法不当会进一步恶化寻优时间，优化插值方法是提高水库调度计算效率的一种有效途径；

2)基于分段线性函数的水库特征曲线读取方式合理、可行，该方法可在不改变优化算法寻优精度的前提下改善算法的寻优时间，在高效的插值算法的基础上还可以缩短约一半的寻优时间；

3)加速策略具有较强的普适性，几乎适用于所有的水库调度问题。

结合实际调度问题以及并行计算技术进一步提高水库调度模型的求解效率将是下一步的研究重点。

[1]纪昌明，李继伟，张新明，等.梯级水电站短期发电优化调度的免疫蛙跳算法应用研究[J].水力发电学报，2014，34(1)：29-36.

JI Changming,LI Jiwei,ZHANG Xinming,et al.Application of immune-shuffled frog-leaping algorithm to optimized operation of cascade hydropower stations for short-term power generation[J].Journal of Hydroelectric Engineering,2014,34(1):29-36.

[2]王森，程春田，武新宇，等.自适应混沌整体退火遗传算法在水电站群优化调度中的应用[J].水力发电学报，2014，33(5)：63-71.

WANG Sen,CHENG Chuntian,WU Xinyu,et al.Application of self-adaptive chaos whole annealing genetic algorithm to optimal operation of hydropower station groups[J].Journal of Hydroelectric Engineering,2014,33(5):63-71.

[3]李文莉，李郁侠，任平安.基于云变异人工蜂群算法的梯级水库群优化调度[J].水力发电学报，2014，33(1)：37-42.

LI Wenli,LI Yuxia,REN Pingan.Optimal operation of cascade reservoirs based on cloud variation-artificial bee colony algorithm[J].Journal of Hydroelectric Engineering,2014,33(1):37-42.

[4]纪昌明，李继伟，张新明，等.梯级水电站短期发电优化调度的免疫蛙跳算法应用研究[J].水力发电学报，2014，34(1)：29-36.

JI Changming,LI Jiwei,ZHANG Xinming,et al.Application of immune-shuffled frog-leaping algorithm to optimized operation of cascade hydropower stations for short-term power generation[J].Journal of Hydroelectric Engineering,2014,34(1):29-36.

[5]明波，黄强，王义民，等.基于改进布谷鸟算法的梯级水库优化调度研究[J].水利学报，2015，46(3)：107-115.

MING Bo,HUANG Qiang,WANG Yimin,et al.Cascade reservoir operation optimization based-on improved cuckoo search[J].Journal of Hydraulic Engineering,2015,46(3):107-115.

[6]明波，黄强，王义民.基于改进布谷鸟算法的梯级水库长期优化调度研究[J].水利水电快报，2015，36(4)：9-13.

MING Bo,HUANG Qiang,WANG Yimin.Long-term optimal operation of cascade reservoir based-on improved cuckoo search[J].Water Resources and Hydropower Information,2015,36(4)：9-13.

[7]刘攀，郭生练，李玮，等.遗传算法在水库调度中的应用综述[J].水利水电科技进展，2006，26(4):78-83.

LIU Pan,GUO Shenglian,LI Wei,et al.A review of application of genetic algorithm to reservoir operation[J].Advances in Science and Technology of Water Resources,2006,26(4):78-83.

[8]彭安邦，彭勇，周慧成，等.跨流域调水条件下水库群联合调度图的多核并行计算研究[J].水利学报,2014,45(11):1284-1292.

PENG Anbang,PENG Yong,ZHOU Huicheng,et al.Multi-core parallel computation for deriving joint operating rule curves in multi-reservoir system under the condition of inter-basin water transfer[J].Journal of Hydraulic Engineering,2014,45(11):1284-1292.

[9]王森，程春田，武新宇，等.梯级水电站群长期发电优化调度多核并行随机动态规划方法[J].中国科学：技术科学，2014，44 (2)：209-218.

WANG Sen,CHENG Chuntian,WU Xinyu,et al.Parallel stochastic dynamic programming for long-term generation operation of cascaded hydropower stations [J].Scientia Sinica Technologica,2014,44(2):209-218.

[10]张忠波，吴学春，张双虎，等.并行动态规划和改进遗传算法在水库调度中的应用[J].水力发电学报，2014，33(4)：21-27.

ZHANG Zhongbo,WU Xuechun,ZHANG Shuanghu，et al.Parallel dynamic programming and improved genetic algorithm and their application to reservoir operation[J].Journal of Hydraulic Engineering,2014,33(4):21-27.

[11]万新宇，王光谦.基于并行动态规划的水库发电优化[J].水力发电学报，2011，30(6)：166-170,182.

WAN Xinyu,WANG Guangqian.Parallel dynamic programming for hydropower generation optimization[J].Journal of Hydraulic Engineering,2011,30(6):166-170,182.

(责任编辑周蓓)

Study on acceleration strategy for optimizing reservoir operation model of multi-reservoir systems

MING Bo,HUANG Qiang,WANG Yimin,LIU Dengfeng,GUAN Jian

(State Key Laboratory Base of Eco-hydraulic Engineering in Arid Area，Xi’anUniversity of Technology，Xi’an 710048，China)

With an aim at dealing with the defeats of long-time consumption in seeking solution to the operation model for traditional multi-reservoir systems,this paper suggests a kind of acceleration strategy of the calculation program.Through transforming the interpolation mode of reservoir feature curves in the process of traditional reservoir operation optimization and in terms of the pre-construction of piecewise linear function of reservoir feature curve node data,the readings of reservoir feature curves can be realized by means of the piecewise linear function to replace the traditional interpolation method.With the hydroelectric operation of a cascade reservoir under typical reservoir inflows as the case study,the cuckoo search algorithm is selected to carry out the optimal calculation and to compare traditional interpolation strategy with the acceleration strategy.The research findings indicate that the acceleration strategy based on the piecewise linear function can obviously shorten the calculation time consumption,and at the same time,this acceleration strategy can hardly affect the algorithm convergence,optimal results and its stability.Accordingly,the acceleration strategy based on the piecewise linear function is rational and reliable as well as a kind of practical and effective method to improve the optimization efficiency of reservoir operation models.

multi-reservoir system; optimal operation; piecewise linear function; acceleration strategy; cuckoo search algorithm

10.19322/j.cnki.issn.1006-4710.2016.01.012

2015-06-02

水利部公益性行业科研专项经费资助项目(201501058)；国家自然科学基金资助项目(51179148，51179149，51309188)；陕西省重点科技创新团队资助项目(2012KCT-10)；陕西省教育厅重点实验室资助项目(13JS069)；陕西省科技统筹创新工程计划资助项目(2013SZS02-Z02)

明波，男，硕士生，研究方向为水资源系统分析。E-mail:mingboctgu@163.com

黄强，男，教授，博导，博士，研究方向为水资源系统分析。E-mail：wresh@mail.xaut.edu.cn

TV697.1+1

A

1006-4710(2016)01-0063-07