基于单神经元PSD的纸浆浓度控制算法研究

黄亚南　张爱娟　胡慕伊

(南京林业大学江苏省制浆造纸科学与技术重点实验室,江苏南京,210037)



·PSD控制算法·

基于单神经元PSD的纸浆浓度控制算法研究

黄亚南张爱娟胡慕伊*

(南京林业大学江苏省制浆造纸科学与技术重点实验室,江苏南京,210037)

稳定的纸浆浓度是保证纸张质量的重要因素,但是纸浆浓度本身又处于长期不可预测的波动中。针对常规方法无法解决纸浆浓度模型的不确定、大时滞、时变性等特点带来的控制问题,提出了一种单神经元PSD的控制算法。利用增益自调整中的PSD算法改善单神经元响应慢的特性,使其增益具有自调整功能,设计出一种不依赖模型、实时性好的快速自适应控制算法。在Simulink中,调用s函数进行仿真,结果表明,与单神经元控制算法以及常规PID算法相比,改进的PSD控制算法响应速度快,并有较强的抗干扰性和自适应性。THJSK-1平台中的控制研究也表明该算法具有可行性。

纸浆浓度；PSD算法；单神经元；增益自调整；s函数

制浆造纸的过程中,由于工艺需要,浆料一直处于脱水、加水的动态过程,这种实时变换的过程导致纸浆浓度波动较大,直接影响纸张的最终质量,也不利于减少原料的消耗；同时浓度的调节过程是一个纯滞后的过程,其滞后时间主要受浆料流速、浆泵频率、调浓白水水压以及浓度变送器安装位置等的影响,因此浓度调节控制要求高于其他控制回路。浓度控制的快速性、精确性要求控制器具有较短的上升时间和良好的稳态性能,工艺、设备的实时扰动也决定了控制器要有一定的鲁棒性能,所以采用常规的PID调节无法满足该控制要求,需要采用复杂先进控制系统解决。

文献[1]采用模糊-Smith控制算法控制纸浆浓度,控制效果具有一定的抗干扰性,但是模糊算法中的规则库及隶属函数主观性较强,Simth算法虽能克服纯滞后,但其算法依赖数学模型,因此会影响控制效果的鲁棒性和抗干扰能力。文献[2]采用BP神经网络算法,其算法计算量大,参数在线调整实时性差。文献[3]采用模糊单神经元控制,利用模糊规则在线调整单神经元增益,动态响应时间得到了改善,但是模糊规则使算法复杂化。本文设计了一种单神经元PSD控制算法。单神经元的权系数可以在线学习,实时调整,能够克服被控对象的大滞后、非线性、时变性等特征,因此可以精确地稳定纸浆浓度。分析单神经元算法,其增益K对控制性能影响较大,但其不能在线自调整,难以满足纸浆浓度控制快的要求,因此本研究采取无辨识控制中的增益自调整PSD算法与单神经元结合,使神经元增益系数K随外界变化而变化,提高系统的动态性能。仿真结果表明,该控制算法可以精确地稳定纸浆浓度,控制输出无超调,动态响应速度快,实时控制及抗干扰性能好,具有很好的鲁棒性。

1　纸浆浓度控制系统

在造纸过程中,纸浆浓度是需要控制的重要变量之一,不但影响每个生产过程中的浆料质量,而且还影响纸张质量[4]。稳定抄纸过程的上网纸浆浓度,可以使生产过程更稳定、纸张定量波动幅度更小。本课题选取流浆箱纸浆为被控对象进行研究,图1所示为流浆箱纸浆低浓控制系统。

图1　流浆箱纸浆低浓控制系统

在该控制系统中,采用光电式浓度变送器CT,将测量到的浓度信号值送到浓度控制器CRC。控制器通过该测量值与给定值,经过一定的控制规律(本研究采用单神经元PSD控制算法)发出控制信号,稀释水阀门执行命令。该纸浆浓度控制系统中增加除气罐和玻璃管的流程是为了实现流速不变、停浆时自动冲洗、除去气泡,以减少被控对象纸浆浓度的干扰项,保证纸浆浓度测量结果的精准性。显然,这种流程加大了系统的纯滞后时间,而在实际运行中,纸浆浓度应具有较快的响应速度,控制偏差应被控制在+7%左右,采用常规PID算法不能满足控制要求,因此本研究采用先进单神经元PSD控制算法作为控制器的控制规律,设计的控制系统结构框图如图2所示。

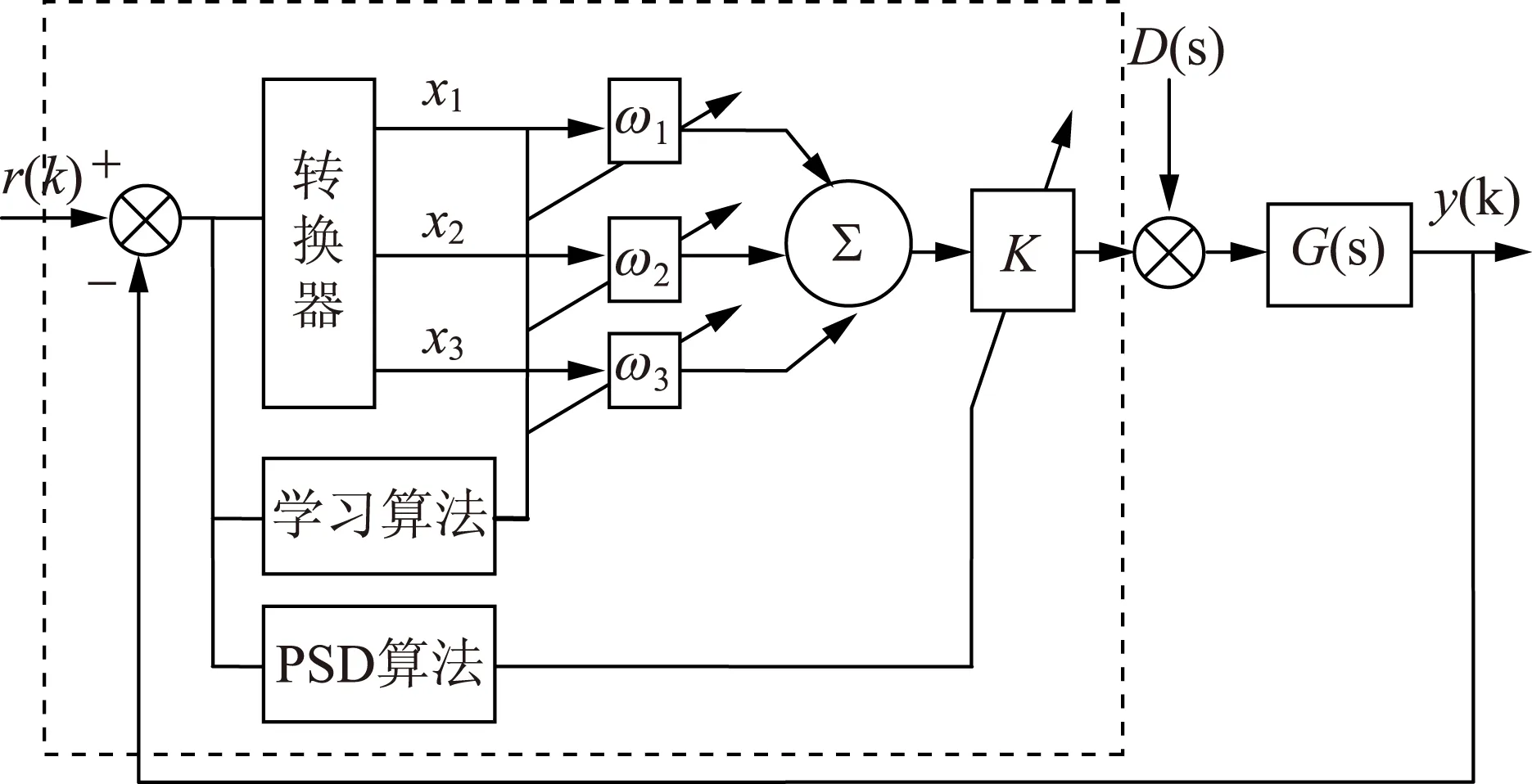
图2　基于单神经元PSD算法的控制系统框图

图2中,r(k)为给定值,D(s)为浆泵频率波动、白水水压波动等干扰传递函数,G(s)为被控对象的传递函数,y(k)为系统的输出,虚线框内为本研究控制器算法。当测量值与给定值不一致时,控制器根据误差和误差的变化计算出神经元算法所需的状态变量x1,x2,x3,其加权系数ω1、ω2、ω3可以在线自学习,而单神经元PSD控制算法则使神经元增益系数K具有在线自学习作用,从而达到既快速又准确的控制要求。

2　单神经元PSD控制算法

2.1单神经元PID算法

单神经元自适应PID的结构框图见图2虚线部分。由图2可知,转换器的输入为被控对象输出值y(k)和给定值r(k),两者相减得到误差信号,神经元所需的学习状态由转换器计算得到：

(1)

xi在k时刻的加权系数为ωi(k),K为神经元的增益系数,单神经元智能控制器的输出见式(2)。

(2)

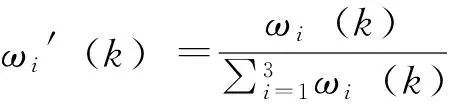
(3)

式中,ηI、ηP、ηD分别为积分、比例、微分学习速率常数,相当于常规PID的P、I、D参数。与常规PID不同的是,在参数整定好之后,常规PID参数不能改变,因此当模型失配或存在外界干扰时,常规PID参数则无法满足控制要求,甚至出现不稳定情况。而单神经元的权值能根据系统的改变而改变,根据外界的变化情况进行自我调整,因此具有很强的抗干扰性能。从权值的调整公式可以看出权系数的自我调整具有非线性逼近能力,也因此具有良好的稳态性能,但根据经验e(k-2)对权值的学习贡献可以忽略不计,其存在会增大计算量,减慢收敛速度。因此可对式(2)进行改进,将xi(k)改为e(k)+Δe(k),见式(4)。

ωi(k+1)=ωi(k)+ηe(k)u(k)(e(k)+Δe(k))

(4)

为保证收敛性,权系数的调整按照目标函数ωi(k)的负梯度方向搜索。

众多单神经元的研究[5- 6]表明, 单神经元的增益系数K是系统最敏感的参数。单神经元动态调节过程上升平稳,但是响应时间很长,主要原因为其增益系数K不能在线自调整,稳定性与快速性不能兼得。当K为固定值时,K值越大,响应越快,但其稳定性也变差,因此希望K值能够在系统响应的不同阶段具有不同大小的值。

2.2基于无辨识PSD算法调整增益系数K

根据误差的几何特性, Marsik和Strejc提出无辨识的自适应PSD控制算法的增量形式，见式(5)。

(5)

式中,K(k)为控制器的增益系数,Tv(k)为控制器参数,两者的校正算法见式(6)。

ΔTv(k)=L*sgn[|Δe(k)|-Tv(k-1)|Δ2e(k)|]

(6)

式中,0.05≤L*≤0.1。

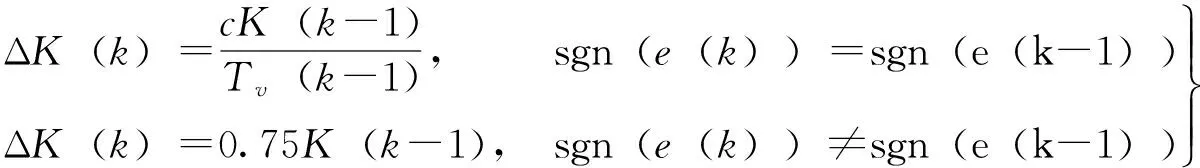
(7)

式中,0.025≤c≤0.05。

PSD算法在本控制系统中的意义为：当纸浆浓度偏离给定值时,控制器开始根据误差进行计算输出。误差同号时,说明误差有变大的趋势,则增大增益值,K(k)的增大有利于尽快接近纸浆浓度给定值；当误差异号时,K(k)呈0.75倍的速度缩减,精细调节,以避免出现超调。

2.3单神经元与PSD算法的结合

将式(2)与式(5)相比较,两者有相同的结构,所以将两者结合具有可实现性。本研究以单神经元的控制规律为基础,以保持神经元非线性逼近能力和权值在线自学习能力,将PSD控制算法中的K(k)自调整规律应用到单神经元最敏感的增益系数K中,形成单神经元PSD控制算法。为了保证算法的收敛性,K的约束条件[7]见式(8)。

(8)

式中，K0为开环增益系数。

3　仿真研究

选取一个典型的纸浆浓度模型作为流浆箱纸浆低浓度的传递函数，见式(9)。

(9)

本研究由阶跃响应法得到被控对象的传递函数,并将其进行采样时间为1 s的离散化,其模型见表1。

表1　被控对象数学模型

根据对象的传递函数以及单神经元算法原理,在Simulink中构造了仿真模型图,如图3所示。其中s-function模块是利用S函数编写的单神经元PSD控制算法,权值及增益的在线自调整语句如下所示：

functionsys=mdlUpdate(t,x,u,ni,np,nd)

sys(1)=x(1)+ni*u(4)*u(1)*(2*u(1)-u(2));

sys(2)=x(2)+np*u(4)*u(1)*(2*u(1)-u(2));

sys(3)=x(3)+nd*u(4)*u(1)*(2*u(1)-u(2));

sys(4)=x(4)+0.075*sign(abs(u(1)-u(2))-x(4))*abs((u(1)-u(2))*(u(1)-u(2)));

else

sys(5)=0.75*x(5);

end

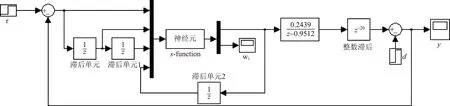
图3　基于单神经元PSD控制算法的纸浆浓度仿真模型图

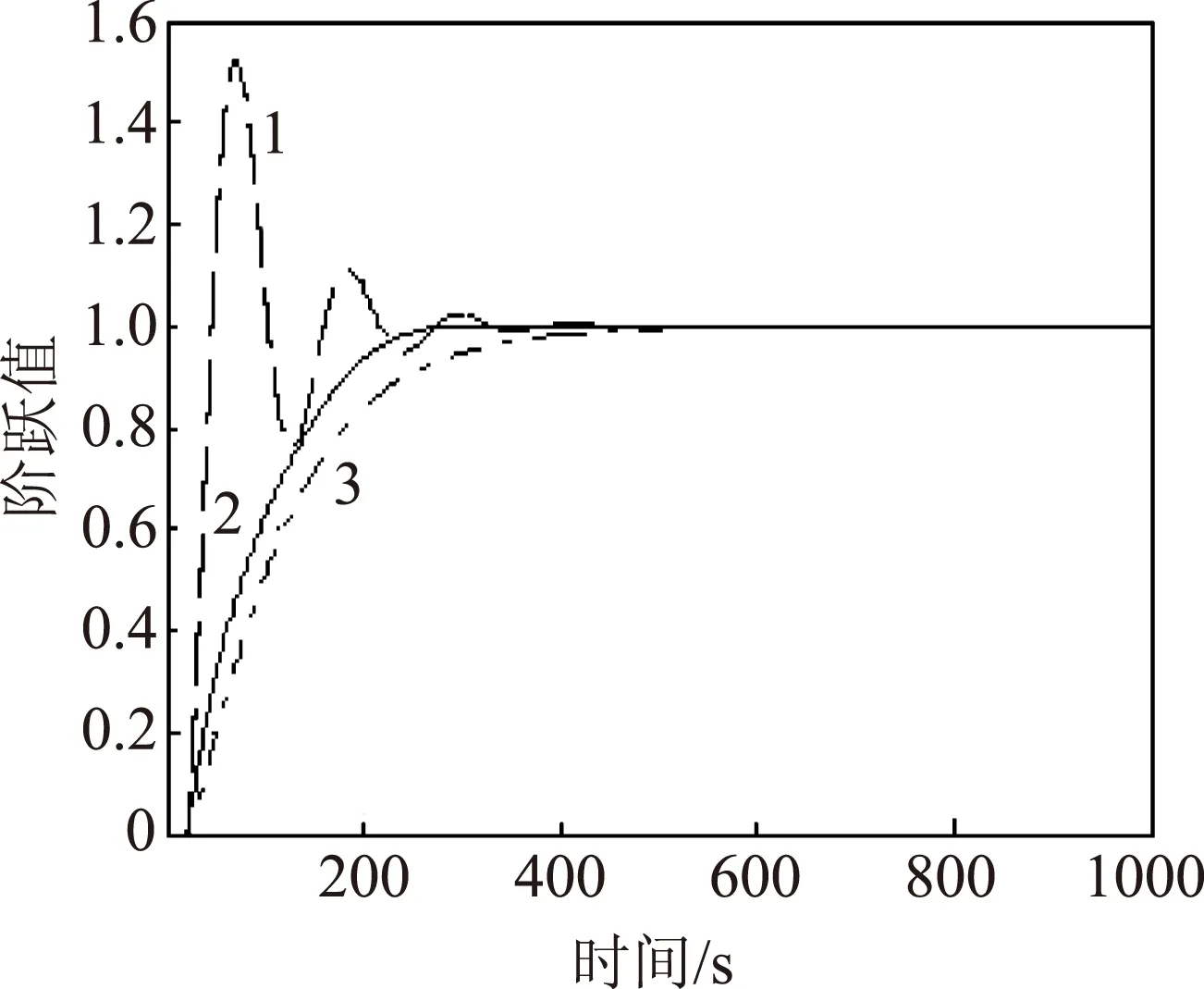
图4　不同算法下的阶跃响应图

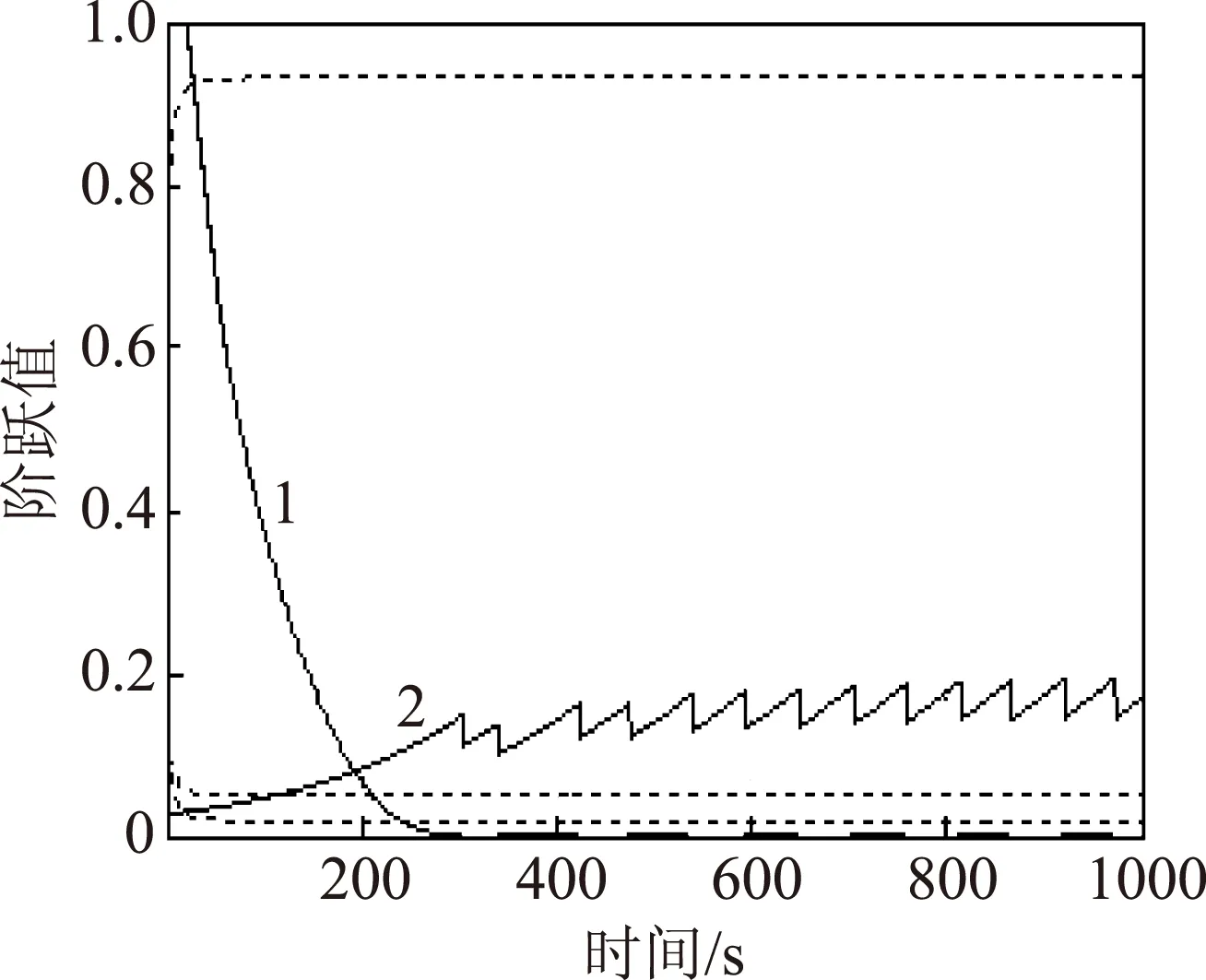
图5　单神经元PSD控制算法中权值及增益的自调整过程图

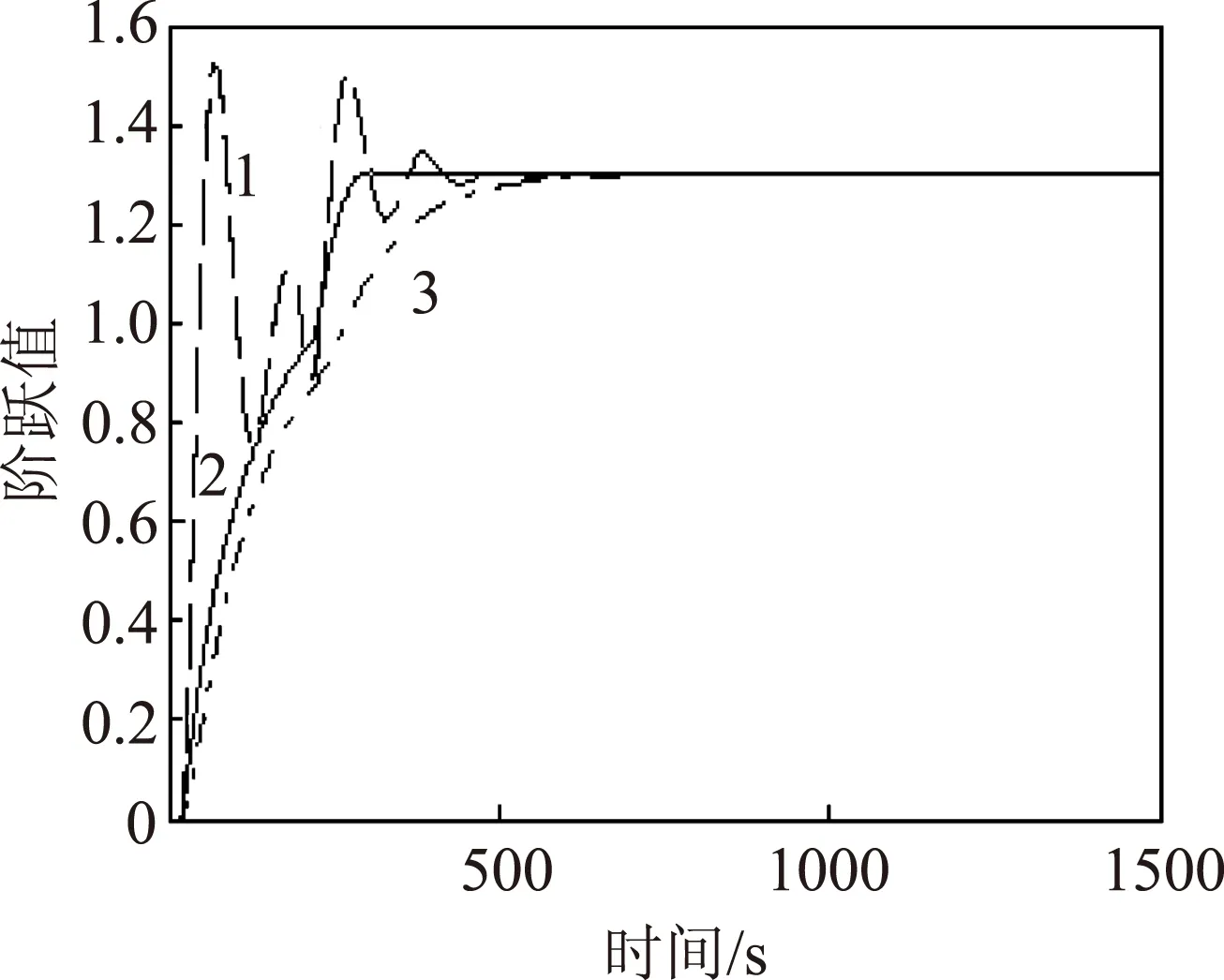
图6　在不同算法及二次干扰下的阶跃响应图

3.1不同算法的阶跃响应

为了体现单神经元PSD控制算法的优越性,将常规PID、单神经元PID以及单神经元PSD控制算法在同一窗口中进行仿真。根据4∶1衰减法对常规PID整定,采用试凑法对单神经元PID、单神经元PSD进行整定,得到各自的最佳参数,图4中曲线1、2、3分别为常规PID、单神经元PSD、单神经元PID算法(以下同)的阶跃响应图。

从图4中可以看出，分析曲线1,常规PID输出超调过大,超调达到了50%,在450 s左右才能稳定,无法实现浆浓控制精确性、快速性的要求；分析曲线3,单神经元PID发挥了其非线性逼近的能力,输出基本无超调,但其调节时间较长,在500 s左右,满足不了控制快速性的要求；分析曲线2,单神经元PSD控制算法输出无超调、调节时间短,仅为250 s,明显改善了单神经元响应慢的特性,具有较好的动静态性能,能够满足浆浓控制的要求。

单神经元PSD权值和增益系数K自学习自调整的过程如图5所示。图5中3条虚线代表3个权值的自调整过程,在误差达到一定程度时,权值趋于稳定,当干扰再次出现时,权值就会重新根据外界环境的改变进行学习自调整。实线1是误差的响应曲线,实线2是增益K的响应曲线,误差在从1降到0的过程中,增益K在逐渐增长,当误差为0时,增益波动稳定在一个平均值上,以保证输出的稳定性。因此单神经元PSD上升速度较快,克服了单神经元PID固有的缺点。

3.2在干扰作用下的阶跃响应

在纸浆浓度的调节过程中,浆浓容易受到浆泵频率波动、白水水压波动等二次干扰,由图4可知,3种算法的调节时间均大于250 s,故为了检验3种算法的抗干扰性能,在t=200 s时加入阶跃值为0.3的二次干扰来模拟浆浓受干扰下的调节情况,各种算法的抗干扰响应对比图如图6所示。图6中单神经元PSD控制算法(曲线2)在二次干扰下仍能控制快速、准确,具有较强的抗干扰性。

3.3模型失配的阶跃响应

被控对象浆浓受多种因素的影响,故其模型实时变化,为了模拟这种模型的非线性、时变性等特性,本研究分别将浆浓对象的增益和时延扩大20%,分别如图7和图8所示。仿真结果表明,当对象模型失配时,常规PID震荡次数明显增多,超调量变大、调节时间增长,稳定性变差。相比而言，单神经元PSD控制算法的优越性更加明显,仍能在保持单神经元非线性逼近能力的同时拥有最快的响应速度。和其他两者相比，单神经元PSD控制算法鲁棒性最好,综合性能最好,具有较强的自适应性。

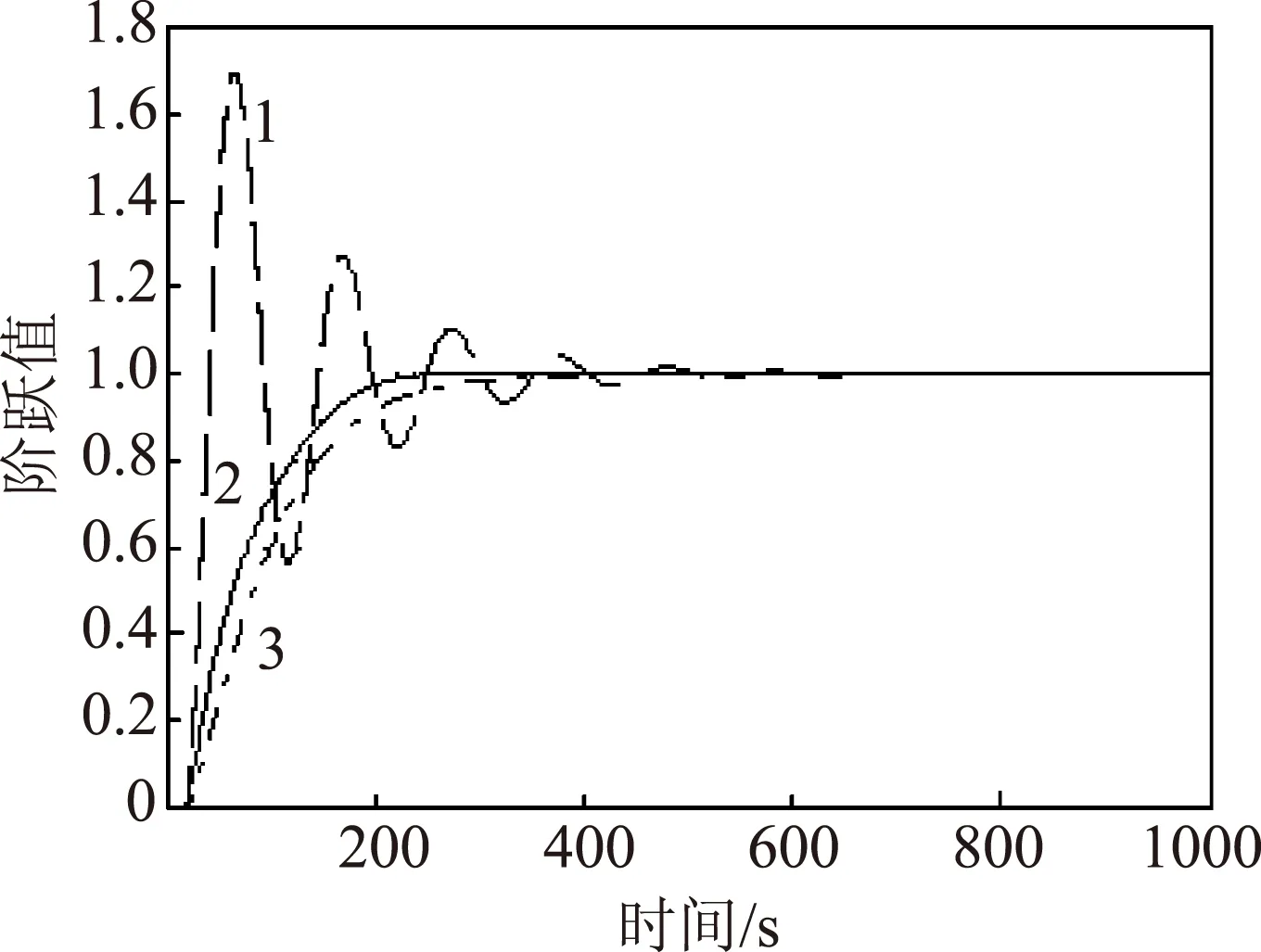
图7　增益失配(增益扩大20%)

图8　时延失配(时延扩大20%)

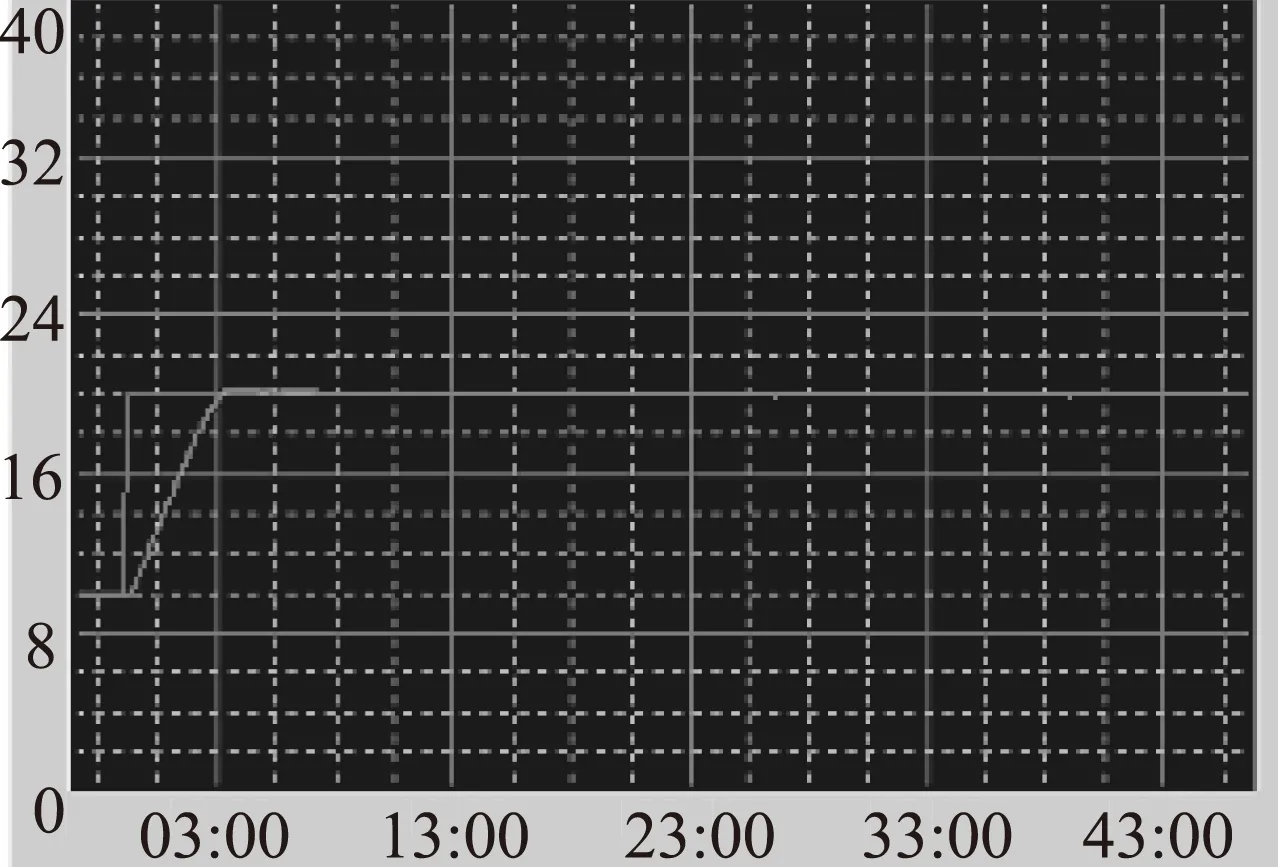
图9　单神经元PSD控制算法的实时控制响应曲线

4　实施控制研究

为了更好的验证单神经元PSD控制算法的优越性,将该算法在“THJSK-1”型实验平台(具有动态过程控制的大时滞、时变性等一般特点)上进行实时控制研究,结果如图9所示。从图9中可以看出,单神经元PSD控制算法具有良好的动静态性能,验证了其优越性。

5　结　论

纸浆浓度的调节过程是一个非线性、时变型、大滞后的过程,本研究选取了流浆箱纸浆浓度进行分析,将单神经元自学习、自适应、非线性逼近的优点和无辨识增益自适应的优点相结合,提出了一种单神经元PSD控制算法。在Simulink中进行仿真,不论是阶跃响应、二次干扰响应,还是模型失配响应,单神经元PSD控制算法都具有明显的优越性。结果表明,单神经元PSD控制算法响应速度快、抗干扰性强、自适应强,成功地弥补了单神经元响应慢的特性。在“THJSK-1”实验平台上的应用,也表明单神经元PSD控制算法具有较强的鲁棒性和较好的动静态性能。因此该算法具有可行性、适合普遍推广。

[1]ZHOU Xiao-ying,ZHANG Gen-bao, MA Hui-hai. A New Fuzzy-smith Control of Pulp Concentration[J]. Journal of Shaanxi University of Science & Technology, 2007, 25(4)： 72.

周小莹, 张根宝, 马汇海. 纸浆浓度的新型模糊-smith控制[J]. 陕西科技大学学报, 2007, 25(4)： 72.

[2]GAO Jun. Controller by PID with BP Neural Network for Pulp Concentration[J]. Light Industry Machinery, 2007, 25(6): 57.

高俊. 纸浆浓度的神经网络PID控制[J]. 轻工机械, 2007, 25(6): 57.

[3]ZHU Wen-na, LI Hong-xing. Adaptive Neuron Control with Fuzzy Self-tuning for Pulp Concentration[J]. Journal of Dalian Institute of Light Industry, 2004, 23(1)： 55.

朱文娜, 李红星. 纸浆浓度的自适应模糊调整神经元控制[J]. 大连轻工业学院学报, 2004, 23(1)： 55.

[4]LIU Huan-bin, BAI Rui-xiang, HU Mu-yi, et al. Automatic Measurement and Control of Pulp and Papermaking Process[M]. Beijing: China Light Industry Press, 2009.

刘焕彬, 白瑞祥, 胡慕伊, 等. 制浆造纸过程自动测量与控制[M]. 北京： 中国轻工业出版社, 2009.

[5]WANG Xing-gui, ZHANG Ming-zhi, LI Qing-ling. Research on Application of Single Neuron PID Controller in Direct Vector Control[J]. Micromotors, 2007, 40(12): 12.

王兴贵, 张明智, 李庆玲. 单神经元PID控制器在直接矢量控制中的应用研究[J]. 微电机, 2007, 40(12): 12.

[6]DENG Xiao, LIU Zong-ling, YANG Zhao. Study on the Control of Black Liquor Level Based on Improved PID Neural Network[J]. Transcations of China Pulp and Paper. 2014. 29(2): 58.

邓肖, 刘宗玲, 杨朝. 改进的PID神经网络在黑液液位控制中的应用[J]. 中国造纸学报. 2014. 29(2): 58.

[7]F Van den Bergh. An analysis of particle swarm optimizers[D]. South Africa: University of Pretoria, 2002.

[8]GE Sheng-min, TONG Shu-hong, ZHOU Bin. Design of a Pulp Consistency Control System[J]. China Pulp & Paper, 2002, 21(3): 50.

葛升民, 童树鸿, 周斌. 纸浆浓度控制系统的设计[J]. 中国造纸, 2002, 21(3): 50.

[9]ZOU Wei, SUN Yu, ZHOU Hai-jun.Simulated Human Intelligence PID Control for Pulp Consistency[J]. China Pulp & Paper, 2005, 24(8)： 44.

邹伟, 孙瑜, 周海君. 纸浆浓度的仿人智能PID控制[J]. 中国造纸. 2005, 24(8)： 44.

[10]LIU Jin-kun. Advanced PID Control and MATLAB Simulation[M]. Beijing: Electronic Industry Press, 2003.

刘金琨. 先进PID控制及其MATLAB仿真[M]. 北京： 电子工业出版社, 2003.

[11]CAO Lu, XIONG Zhi-xin, HU Mu-yi. Simulation and Research on Pulp Consistency Control System[J]. Computer Simulation. 2012, 29(6): 176.

(责任编辑：董凤霞)

Pulp Consistency Control Algorithm Based on Single Neuron Adaptive PSD

HUANG Ya-nanZHANG Ai-juanHU Mu-yi*

(JiangsuProvincialKeyLabofPulpandPaperScienceandTechnology，NanjingForestryUniversity，Nanjing，JiangsuProvince， 210037)

Pulp consistency fluctuates unpredictably all the time. At the same time, the stable pulp consistency is an important factor to guarantee the quality of the paper. The model of pulp consistency is characterized by uncertainty, large time-delay and time-variation, so conventional PID is difficult to obtain good control quality. Therefore, the algorithm based on single neuron adaptive PSD was proposed. In this paper, the PSD algorithm from the identification free control algorithm was added to improve the response rate of single neuron PID control. Its gain was with self-tuning and thus a model-independent and more real-time adaptive fast algorithm was developed . In the Matlab, the s-function of this algorithm was called to simulink dynamically. The results indicated that comparing with conventional PID control and ordinary single neuron PID control , the control algorithm had better response rate, stronger interference rejection and the greater adaptive ability. The real-time control on THJSK-1 experiment platform indicated this control algorithm was feasible.

pulp consistency； PSD algorithm； single neuron； gain scheduling control；s-function

黄亚南女士,在读硕士研究生；研究方向：制浆造纸过程与控制,先进控制。

2015-11-26(修改稿)

江苏高校优势学科建设工程资助项目(PAPD)。

胡慕伊先生,E-mail∶muyi_hu@njfu.com.cn。

TP273

A

10.11980/j.issn.0254- 508X.2016.05.009

(*E-mail: muyi_hu@njfu.com.cn)