静乐井SWY-Ⅱ和LN-3A水位仪的对比分析

胡玉良 程冬焱 李惠玲 穆慧敏 郭宇 刘俊芳

1）山西省地震局，山西省太原市旧晋祠路二段69号 030021

2）太原大陆裂谷动力学国家野外科学观测研究站，太原 030025

3）山西省地震局定襄地震台，山西定襄 035400

0 引言

国内外学者以大量的观测事实论证了水位动态不仅可以直接反映含水层应力应变的变化，还可反映井-含水层水动力条件的变化（国家地震局科技监测司，1994），因此水位动态研究是研究地球某些动力过程和监测地震孕育的重要途径（汪成民等，1988）。

随着 “九五”、“十五”、“十一五”项目的全面建设，流体数字化观测仪器在全国开始投入运行，为水位动态研究提供了丰富的数据（廖丽霞等，2013），以此为基础的地震观测技术由模拟观测向数字化观测发展（耿杰，2008）。“十五”期间，山西省地震局对镇川、朔州、太原、静乐、祁县、介休、孝义、漫水和东郭流体井进行了技术改造，统一安装了由中国地震局地震预测研究所研制的LN-3A水位仪。“十一五”期间，山西省地震局对榆社红崖头流体井和忻州鸦儿坑流体井进行了技术改造，统一安装了由中国地震局地壳应力研究所研制的SWY-Ⅱ水位仪。

“九五”、“十五”项目建设完成后，耿杰等（2001）、黄春玲等（2010）曾做过数字化水位观测资料与模拟观测资料的对比分析，主要针对LN-3型数字水位仪和SW 40-1日记式水位仪或LN-3A型数字水位仪（以下简称 LN-3A水位仪）和 SW 40-1日记式水位仪（以下简称SW 40-1水位仪）。由于SWY-Ⅱ型数字化水位仪（以下简称SWY-Ⅱ水位仪）为新研制的仪器（何案华等，2012），尚未对SWY-Ⅱ水位仪和LN-3A水位仪进行对比分析研究，因此，本文通过在静乐井对新安装的1套SWY-Ⅱ及原有的LN-3A水位仪开展为期3个多月的并行观测，从稳定性、数据一致性、数据精度、系统漂移、水震波、气压效应、自然环境干扰这7方面进行对比分析。

1 对比分析

1.1 仪器运行

2015年4月17日将 SWY-Ⅱ水位仪安装到静乐井，从4月18日开始投入运行，台站值班人员按照流体学科规范要求做好仪器维护、数据预处理、观测日志填写、仪器校测等工作，确保SWY-Ⅱ水位仪产出数据连续、稳定可靠，同时对静乐井原有的LN-3A水位仪的观测数据进行跟踪分析。利用中国地震前兆台网运行评价系统对两套仪器的数据完整率进行统计（表1）。

由表1可知，两套水位仪运行稳定，均未发生故障，数据连续率均达99.99%以上。

表1 静乐井数字水位仪观测数据完整率对比

1.2 数据一致性分析

首先对静乐井SWY-Ⅱ、LN-3A两套水位仪曲线形态进行定性分析，提取2015年4月18日～7月31日的分钟值数据，如图1所示，从曲线形态上看，两套仪器的趋势是一致的，从图上也能明显看出在水震波记录的幅度上有差异（见本文1.6节），为了更详细地说明两套仪器记录数据的差异是否随时间而变化，将两套仪器产生的分钟值数据相减，得到的差值如图2所示。两套仪器除了在地震波记录的幅度上有差异外，在其余时间内差值最小值是0.091m，最大值是0.115m，平均差值为0.103m，差值变化幅度不超过0.024m。平均差值不在零附近主要是由于两套仪器之间存在系统误差，通过修正SWY-Ⅱ或LN-3A的参数值即可解决，差值曲线形态和变化幅度说明两套仪器的一致性非常好。

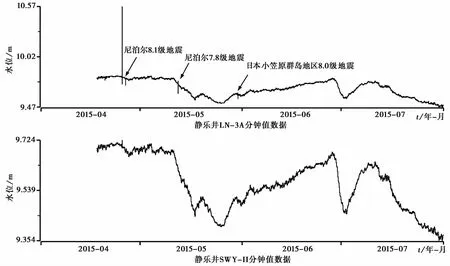
图1 静乐井2015年4月18日～7月31日数字水位仪分钟值数据对比曲线图

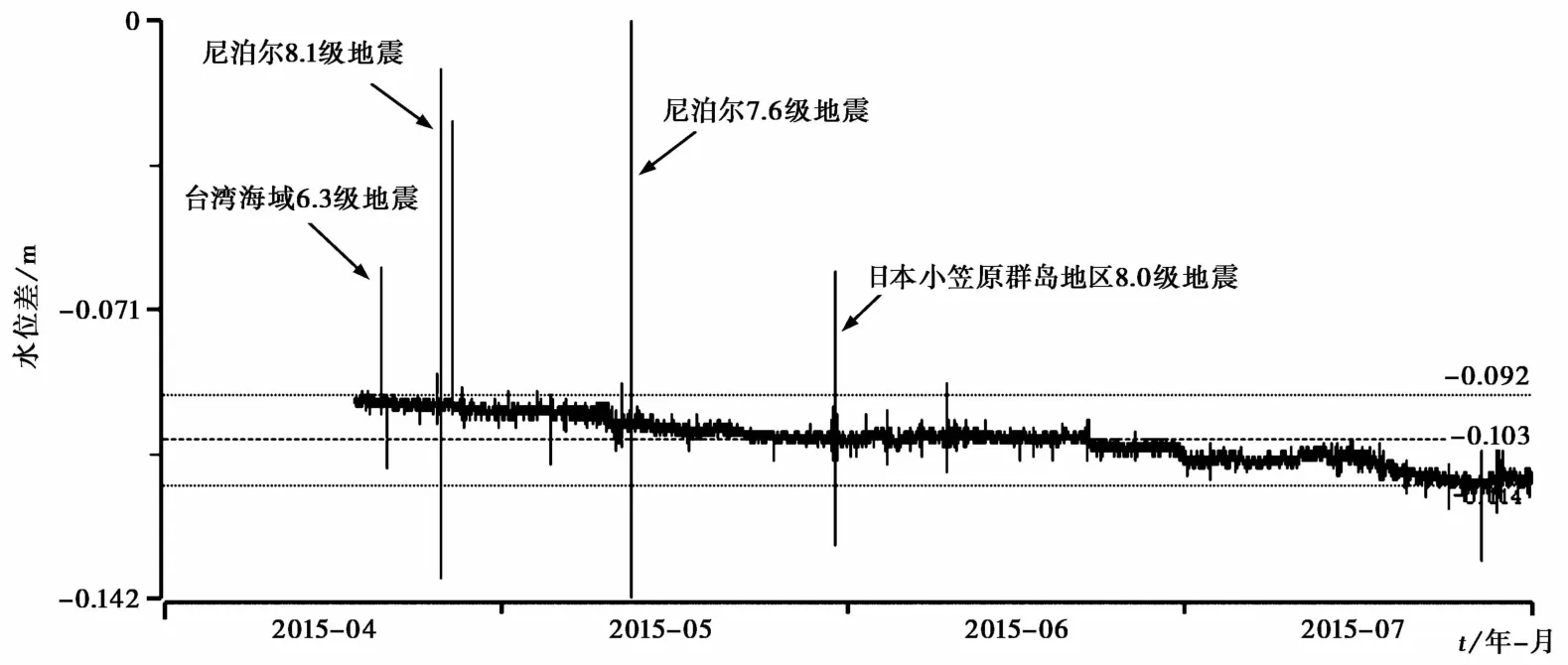
图2 静乐井2015年4月18日～7月31日数字水位仪分钟值数据差值曲线图

标准偏差越小，表明测量的分散度越小，测量的精度越高，用标准偏差可以表征测量精度。在无系统误差的情况下，一般把标准偏差作为测量误差（何平，1994）。由于两套仪器均放置在水井中，当井水位发生变化时两套仪器的产出数据也会随之发生变化。为了计算两套仪器的标准偏差，从而确定两套仪器的精度，需要按照一定的条件对两套仪器产出的分钟值数据进行筛选，条件为：①选取的时间段必须短；②确保两套仪器观测数据要平稳，波动要尽可能地小。基于以上两点，选取了2015年4月23日7：00～8：00的分钟值，使用 SPSS软件做单因素方差分析（罗纳德，2010；里斯，2011），计算了两套仪器的标准偏差。

为了使用 SPSS软件对两套仪器时均值数据做配对样本 t检验（罗纳德，2010；里斯，2011），需要消除两套仪器之间存在的系统误差。本文对LN-3A水位仪时均值进行了修正，具体修正过程如下：SWY-Ⅱ、LN-3A水位仪 2015年 4月 18日零点数据分别是 9.693和9.787，两者相差0.094，故对LN-3A水位仪从2015年4月18日～7月31日之间所有时均值数据都减去0.094即可。

1.2.1 单因素方差分析

方差分析就是分析不同水平下各个总体的均值是否有显著的差异。统计推断方法是计算F统计量，进行F检验。单因素方差分析指的是自变量只有一个的方差分析，计算公式为（邱轶兵，2008）

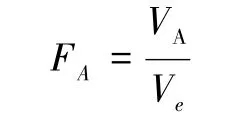
其中，VA为因素偏差平方和；Ve为误差平方和；FA为一个统计量，服从自由度为（FA，fe）的F分布，其中FA为因素偏差平方和自由度；fe为误差平方和自由度。给定α＝0.05，如果FA≥F0．05（fA，fe），就说明因素A变化的影响大于误差的影响，即该因素变化显著。

利用SPSS软件对 SWY-Ⅱ水位仪和 LN-3A水位仪2015年4月23日7：00～8：00之间的分钟值数据进行单因素方差计算，计算结果如表2。

表2 描述统计

由表2可知，LN-3A水位仪标准偏差是0.000279，SWY-Ⅱ水位仪标准偏差是0.00022，说明两套仪器测量精度基本无差异，并且均优于0.001m。

1.2.2 配对t检验基本步骤

首先，提出两配对样本t检验的假设为 H0，两样本均值 μ1、μ2无显著差异，即 H0＝μ1-μ2＝0。

利用SPSS软件对SWY-Ⅱ水位仪和LN-3A水位仪2015年4月18日～7月31日的时均值数据进行配对t检验，计算结果如表3。

表3 配对t检验结果

从表3可以得到SWY-Ⅱ水位仪和LN-3A水位仪数据之差的均值、标准差、均值标准误差、95%的置信区间以及t检验值、自由度和双侧概率值。通过分析可知，双侧概率值小于0.05，说明两套仪器均值存在差异；两套仪器均值相差0.009m，标准偏差为0.005m，说明两套仪器均值虽有差异，但均在观测允许的误差范围内，因此，从观测的角度来说，可认为两套仪器均值是一致的。

1.3 数据内在质量

井水位潮汐是固体地球潮汐的一种次生效应（汪成民，1988），由于观测井一般深度只有数百米或数千米，处于地球表层，因此地球表层潮汐应力分布会影响静水位反周期性变化（国家地震局科技监测司，1995）。吕芳等（2012）认为静乐井的井-含水层系统对地壳应力-应变有较强的响应能力，本文通过对静乐井两套数字水位仪分钟值数据和理论固体潮进行曲线对比及计算M2波潮汐因子及其观测精度，也印证了这一点。

从图3可以看出，两套水位仪均能记录到完整的日波与半日波，相位同步清晰，幅度较大，与理论固体潮曲线相位一致。

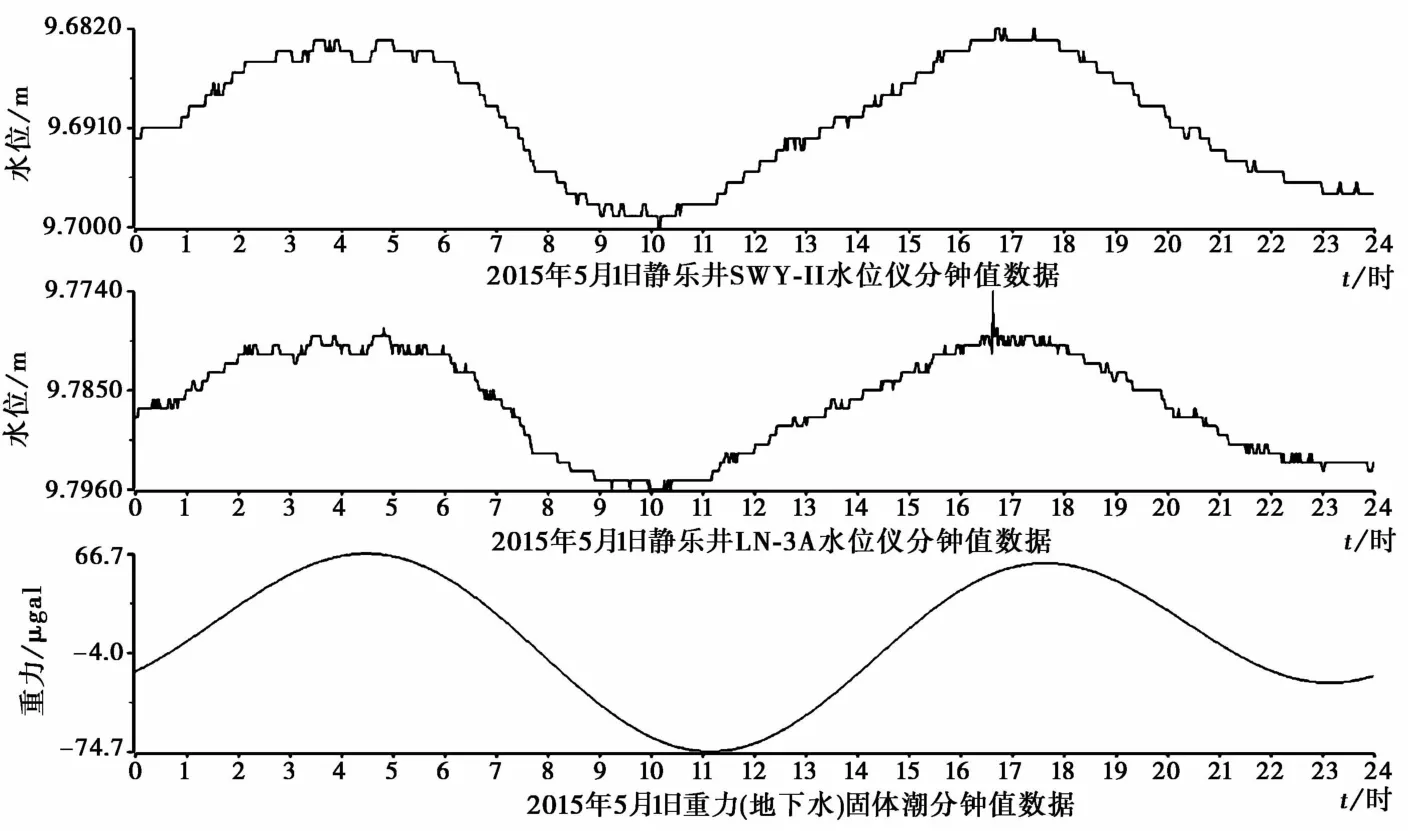
图3 2015年5月1日SWY-Ⅱ、LN-3A水位及理论固体潮时均值数据曲线

使用两套水位仪分钟值数据，利用中国地震前兆台网运行评价系统 2011版软件计算两套水位仪M2波潮汐因子及其观测精度（刘春国等，2015），并进行对比分析，其结果如表4所示。

从表4可以看出，对于M 2波潮汐因子和观测精度，SWY-Ⅱ水位仪均优于LN-3A水位仪。

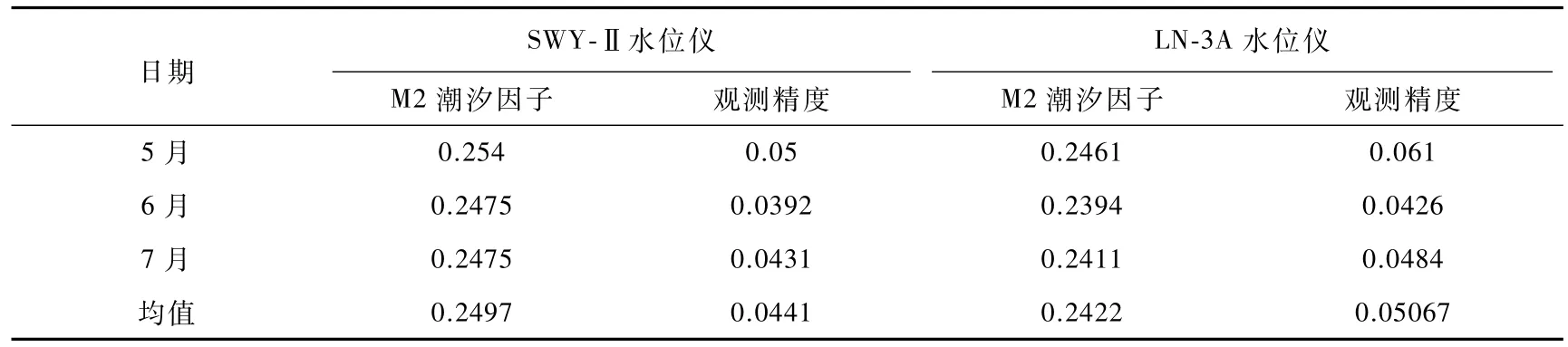
表4 水位仪M 2波潮汐因子及其观测精度对比

1.4 系统漂移

SWY-Ⅱ和LN-3A水位仪传感器均采用扩散硅半导体压力器件。一方面半导体的温度特性使硅压力传感器的零点和灵敏度随温度而发生漂移（孙凤玲等，2007；张艳锋等，2008），导致测量精度会下降（何平等，2008）；另一方面，由于传感器埋深（即传感器探头至水面的距离）会随着时间发生变化，也会导致测量精度发生变化（杨鼎鸿等，2013），因此有必要计算两套数字化水位仪在工作环境下的系统漂移。

由于每天均对静乐井SW 40-1水位仪进行校测，因此可以认为SW 40-1水位仪测量值是准确的，故以SW 40-1水位仪2015年4月18日～6月30日的日均值为基准，与两套数字化水位仪同时段的日均值分别相减，得到两组差值，以此来确定每套仪器随时间变化漂移情况。差值对比曲线如图4所示，SW 40-1水位仪日均值曲线如图5所示。

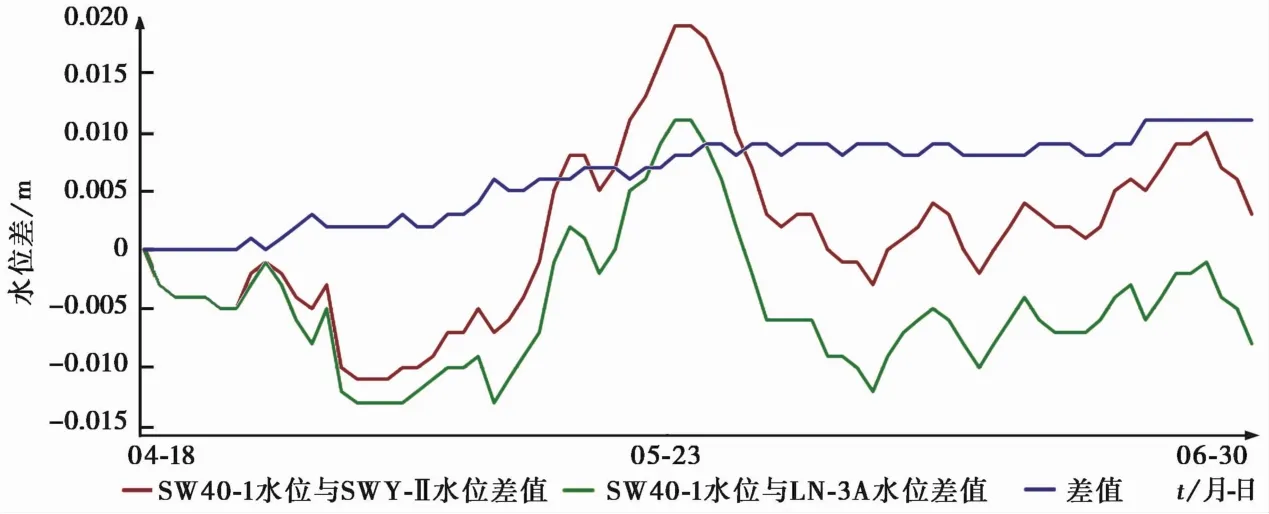
图4 静乐井两套数字水位仪系统误差对比分析曲线

由图4可知，SWY-Ⅱ水位仪正向最大漂移量为0.019m，LN-3A水位仪为0.011m；SWY-Ⅱ水位仪反向最大漂移量为-0.011m，LN-3A水位仪为-0.013m；SWY-Ⅱ水位仪漂移量平均值为0.0014m，LN-3A为-0.0048m。从曲线形态上来看，2条曲线较为一致，只是幅度略有差异；对2条曲线做一阶差分后可以看出，SWY-Ⅱ水位仪的漂移量稍大于 LN-3A，最大相差0.009m，但漂移量都在mm级，这可能是由于两套水位仪压力传感器的特性差异造成的。总体上来说，两套水位仪测量值均会随时间发生不同程度漂移，并且漂移量随时间发生非线性变化，因此两套数字化水位仪均需按照规范要求定期进行校测。

对比图4和5可知，LN-3A和SWY-Ⅱ两套水位仪系统漂移量最大时，静乐井实际水位观测值最小，由此说明水位的上下波动对两套水位探头的压力响应系数有一定的影响。

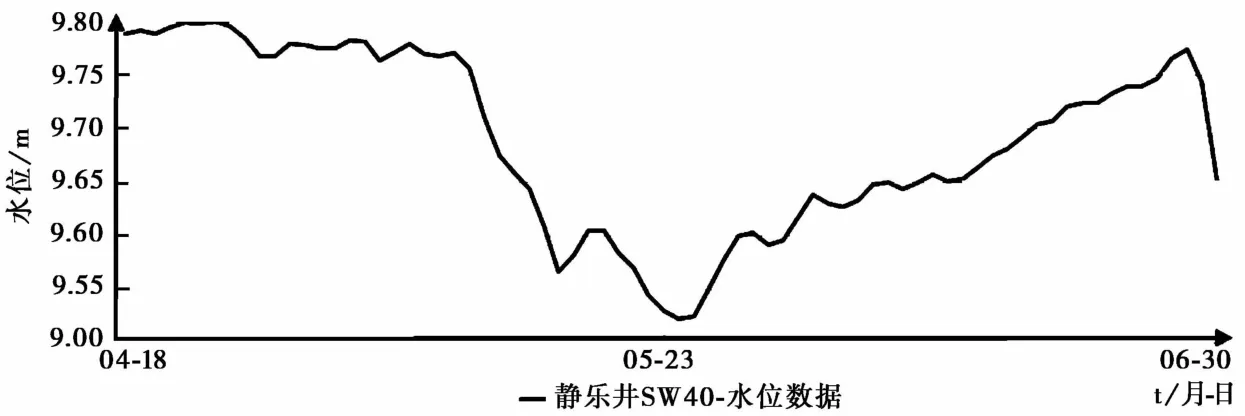
图5 静乐井SW 40-1水位曲线

1.5 气压效应

气压对地下水影响具有普遍性（汪成民等，1988；耿杰等，2001），气压每变化1hPa所引起的水位变化称为井水位气压效率，单位为mm／hPa，利用SPSS软件对静乐井两套水位仪日均值与气压数据进行皮尔逊相关系数计算后发现，SWY-Ⅱ水位仪与气压相关系数为0.307，LN-3A水位仪与气压相关系数为0.293，相关程度均较弱，两套水位仪测值与气压的相关系数较为接近。

1.6 水震波效应

2015年4月～7月，静乐井SWY-Ⅱ和 LN-3A水位仪记录到6级以上地震4次（表5）。

表5 静乐井数字水位仪记录地震情况对照表

地下水位水震波受观测层的岩性、埋深、井孔-含水层间的导水能力、井孔水柱高度、地震地点、震级（耿杰等，2001、2008）及观测仪器（廖丽霞等，2009；廖丽霞等，2013）等诸多因素的影响。分析结果表明，LN-3A和SWY-Ⅱ水位仪在分钟值采样下均能清晰记录到水震波，但震荡时间和震荡幅度均有明显差别，具体原因是由于SWY-Ⅱ水位仪内部采用秒采样，然后将60s数据进行平均后获得分钟值数据，这样相当于SWY-Ⅱ水位仪进行了平均滤波，信号平滑度较好，但降低了灵敏度；而LN-3A水位仪是在每个分钟某一个时刻进行数据采集获得分钟值数据。

由于SWY-Ⅱ水位仪保存了秒采样的水位数据，这里截取了SWY-Ⅱ水位仪2015年4月25日尼泊尔地震前后记录的秒采样数据曲线，如图6所示，通过图6可以看到清晰的水震波，震荡时间为50m in，和LN-3A水位仪相差无几；震荡幅度达到1.757m，比LN-3A水位仪高0.895m。基于此，建议将SWY-Ⅱ水位仪秒采样数据接入到前兆数据管理系统，这样获取的信息更多，有利于进一步研究。

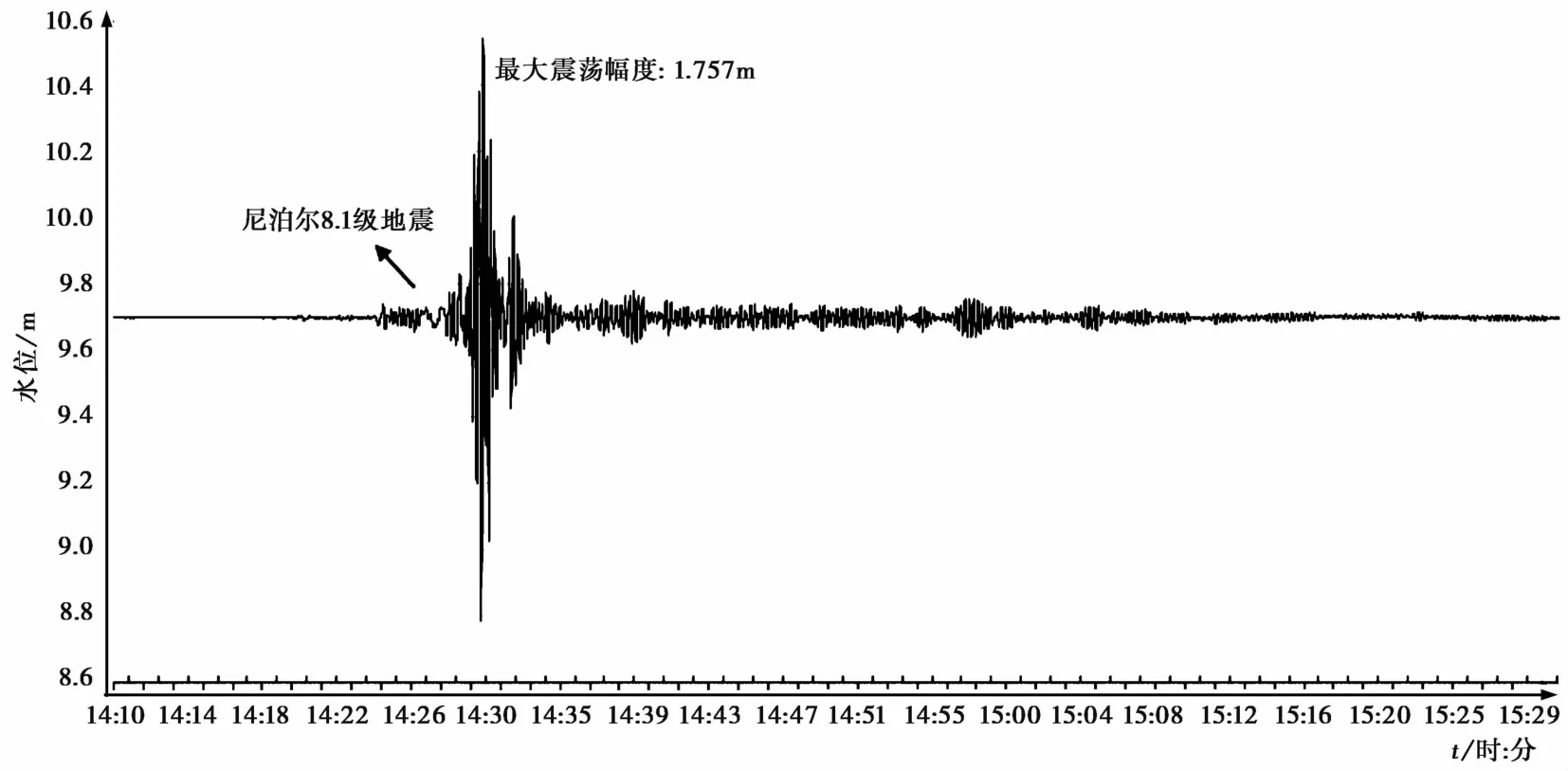
图6 静乐井SWY-Ⅱ水位仪2015年4月25日秒数据曲线

1.7 自然环境干扰

利用前兆台网（台站）观测数据跟踪分析软件查询可知，2015年4月18日～7月31日，LN-3A水位仪记录到自然环境干扰事件5次，其中降水影响4次，雷电影响1次。以5月12日～17日记录的事件为例进行说明，通过与SWY-Ⅱ水位仪同时段观测数据对比可知（图7（b）和（c）），2条曲线形态完全一致，从而说明了观测数据变化与观测系统无关，为了进一步说明是何种因素导致的水位上升，增加了忻州鸦儿坑雨量曲线，并且与2014年数据进行同期对比，如图7所示。

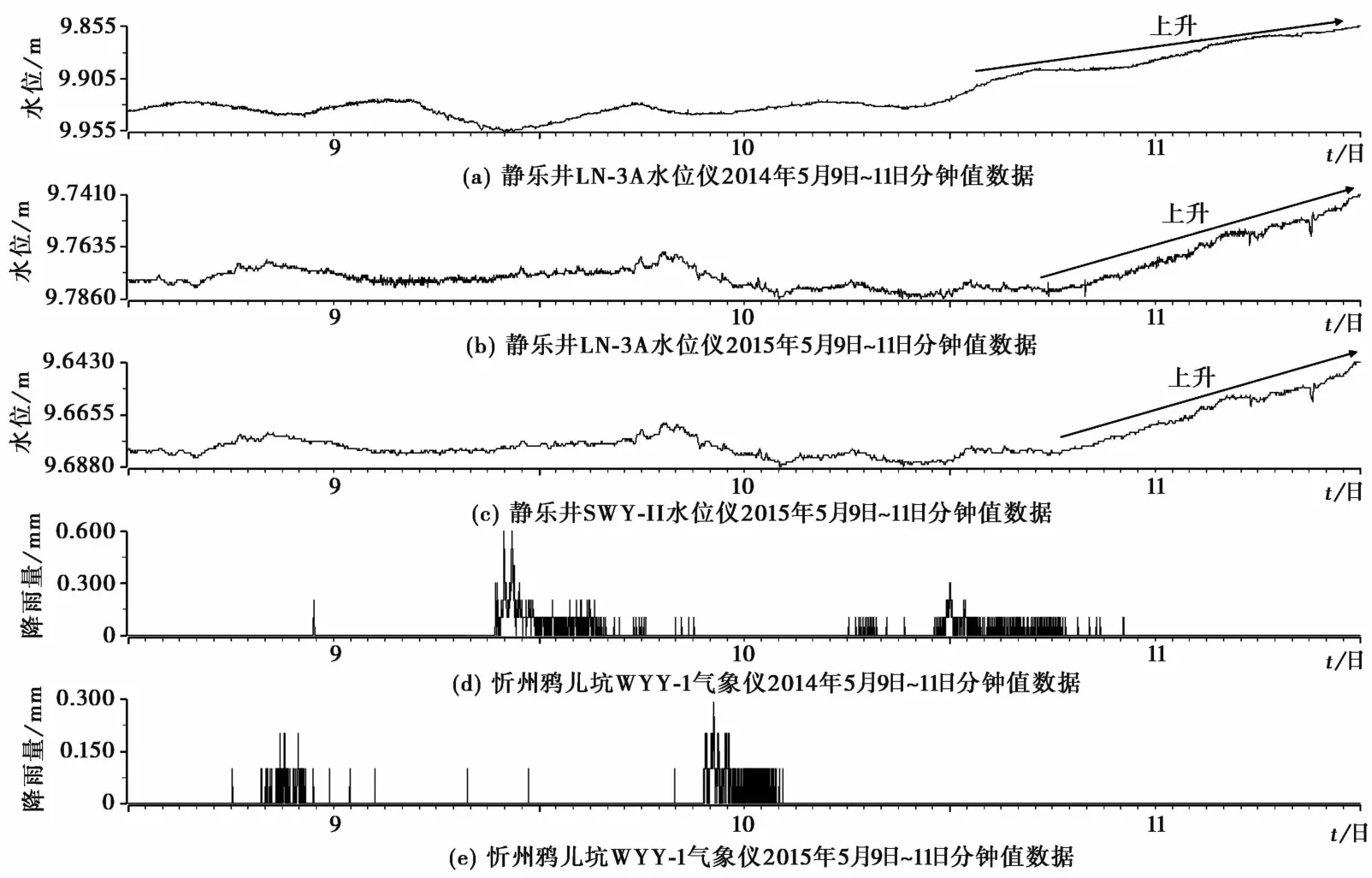
图7 静乐井水位与降雨量同期对比曲线

从图7可以看出，2014年5月9日～11日与2015年5月9日～10日同期均有降雨，导致静乐井水位上升。

2 结论与讨论

两套数字化水位仪在并行运行期间工作稳定，数据完整；通过曲线形态对比，两套仪器一致性非常好；采用相关统计学方法得知，两套数字化水位仪观测数据精度均优于0.001m，产出均值一致性较好；利用相关软件对两套数字化水位仪时均值数据计算了M 2波潮汐因子及其观测精度，结果表明，SWY-Ⅱ水位仪观测精度优于LN-3A水位仪；基于静乐井模拟水位数据，对两套数字化水位仪系统漂移进行了计算，结果显示，两套数字化水位仪均出现不同程度系统漂移，因此在数字化水位仪运行过程中，需对水位传感器定期进行标定校测，确保水位数据真实可靠；两套水位仪水位数据与气压相关性较为一致；分钟值采样下，水震波记录震荡时间及水位振幅有明显差别；自然环境干扰方面，两套水位仪干扰程度较为一致。

通过对比分析发现，两套数字化水位仪在系统漂移及水震波记录方面存在着一些差异，SWY-Ⅱ水位仪秒采样数据记录地震波信息较为丰富，这为下一步深入研究提供了方向。